日本で「集団免疫」戦略は成り立つか
新型コロナについてイギリスの採用した集団免疫戦略が論議を呼んでいる。これは簡単にいうと国内で十分多くの人が感染したら流行が終わるという理論である。これを批判したブログが話題になっているが、これは間違っている。私は日本で集団免疫戦略は成り立つと思う。感染力は、生物学的には基本再生産数R0で決まる。 これは1人の感染者が何人にウイルスをうつすかという指標で、R0=2だとすると2人。その2人がさらに2人にうつすと2nで感染者が増える。
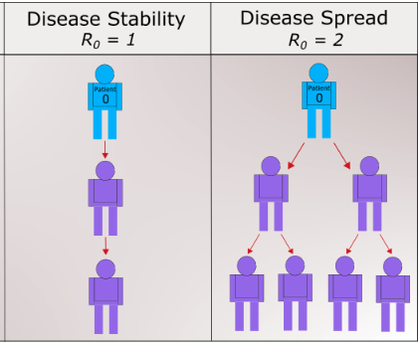
現実の感染速度を決めるのは基本再生産数ではなく、実効再生産数Rである。これはR0と集団の中で免疫のない人の比率xの積で、
R=R0・x
と定義する。上の図でいうと、最初だれにも免疫のない状態ではR=2だが、感染が広がって集団の半分が免疫をもつとR=1になって感染が止まる。疫学の教科書によると、集団免疫が成り立つ免疫比率Hは、次のように決まる。
H=1-1/R0 (*)
この関係はこう考えればわかる:あるウイルスがR0=3だとすると、その集団の3人に1人に免疫があれば2人しか感染しない。2人が免疫を獲得すれば、感染するのは1人になって感染の拡大は終わる。したがってHが1-1/3=2/3のとき、集団免疫が成り立つ。
コロナの集団免疫を論じるとき、多くの人が「国民の60%が感染するまで集団免疫は成立しない」というのは、(*)式でR0=2.5と想定しているからだ。このとき
H=1-0.4=0.6
となるが、Rは下げることができる。わかりやすいのはワクチンで免疫を増やしてxを下げることだが、コロナのようにワクチンのない感染症でも、感染が拡大すると免疫が増えてxが下がり、Rは下がる。また日本のように清潔な国では感染確率が低いのでR0が下がり、Rは下がる。
実効再生産数は指数関数できいてくるので、これを下げる効果は大きい。(*)式でR0をRに置き換え、たとえば(日本で観測されている値に近い)R=1.25とすると、H=0.2となる。これは人口の20%(2400万人)が感染すると流行が終わるということで、インフルエンザに近い。
これは最悪のケースで、春になったらコロナが消える可能性もあり、感染をおさえて時間を稼いでいればワクチンができる可能性もある。要するに唐木英明氏もいうように
新型コロナ騒動は、集団免疫を得るまでは終わらない。そうであれば、厳しい対策により感染者をゼロに近づけようと努力するのではなく、ドイツや英国に倣つて、医療崩壊を起こさないように注意しながら、ある程度の感染を容認して、集団免疫を得ることを考えるべきではないだろうか。
追記:専門家会議が「日本の実効再生産数はおおむね1」という報告を出したので、アゴラで説明した。
続きは3月16日(月)朝7時に配信する池田信夫ブログマガジンで(初月無料)。
国の専門家会議は2月24日に「これから1-2週間が急速な拡大に進むか、収束できるかの瀬戸際となります」と述べたが、3月9日の見解ではこう書いている。
これは重要なデータである。実効再生産数は感染力を示す指標で、これが「おおむね1」ということは、新型コロナの感染がピークアウトした可能性を示唆するからだ。新規患者数も死者も、先週で頭打ちになっている。これは検査キットの不足などの原因も考えられるが、感染が飽和した可能性もある。
続きはアゴラで。
これまでに国内で感染が確認された方のうち重症・軽症に関わらず約8 0%の方は、他の人に感染させていません。また、実効再生産数(感染症の流行が進行中の集団のあ る時点における、1人の感染者から二次感染させた平均の数)は日によって変動はあるものの概ね1程度で推移しています。
これは重要なデータである。実効再生産数は感染力を示す指標で、これが「おおむね1」ということは、新型コロナの感染がピークアウトした可能性を示唆するからだ。新規患者数も死者も、先週で頭打ちになっている。これは検査キットの不足などの原因も考えられるが、感染が飽和した可能性もある。
続きはアゴラで。
0 件のコメント:
コメントを投稿