NAMs出版プロジェクト: 新・経済循環フロー図:試作
http://nam-students.blogspot.jp/2015/10/blog-post_20.html
NAMs出版プロジェクト: フロー循環図
http://nam-students.blogspot.jp/2015/08/blog-post_38.html
NAMs出版プロジェクト: マルコフ連鎖:メモ
http://nam-students.blogspot.jp/2015/10/blog-post_54.html(本頁)
http://nam-students.blogspot.jp/2015/10/blog-post_72.html
NAMs出版プロジェクト: アンチ・オイディプス 資本主義と分裂症:目次
http://nam-students.blogspot.jp/2012/12/blog-post_5039.html
http://nam-students.blogspot.jp/2015/10/1979-john-maynard-keynes-treatise-money.html
《(11) マルコフ連鎖について、またこれの生物種および文化的形成物の適用については、cf. Raymond Ruyer*, La Genèse des formes vivantes , ch. VIII. コードの剰余価値の諸現象は、「半偶発的連鎖」という見方によって的確に説明されるが、リュイエは、繰り返しこれを分裂症的言語と比較している。》
(ドゥルーズAO第4章原注より)
(小倉拓也書評250頁より)
*
レイモン・リュイエ Raymond Ruyer (1902-1987)邦訳なし
ドゥルーズがAOで要約した『生物の形態の発生』の邦訳が待たれる。(リュイエはDR#4、MP#11でも言及されている。)
https://en.wikipedia.org/wiki/Raymond_Ruyer
Raymond Ruyer (1902 -1987) was a French philosopher in the late 20th century. Author of many important works, he covered several topics such as the philosophy of biology, the philosophy of informatics, the philosophy of value and others. His most popular book is The Gnosis of Princeton in which he presents his own philosophic views under the pretence that he was representing the views of an imaginary group of American scientists. He developed a theory of consciousness of all living matter, named panpsychism, which was a major influence on philosophers such as Simondon, Deleuze and Guattari.
• Éléments de psycho-biologie - Presses Universitaires de France, Paris, 1946
• La genèse des formes vivantes - Flammarion, Paris, 1958
• La gnose de Princeton - Fayard, Paris, 1974
**
ソヴァニャルグ Anne Sauvagnargues (『ドゥルーズと芸術』未邦訳)
未邦訳と書いたが、マルコフ連鎖に言及した同書第七章「リゾームと線」(小倉拓也他訳)が『ドゥルーズ 没後20年 新たなる転回』(201510河出書房新社pp42-63)に所収された。
まもなく発売:アンソロジー『ドゥルーズ』、ほか : ウラゲツ☆ブログ
http://urag.exblog.jp/21766967/
《第一線のドゥルーズ研究者の対談や、国内外の刺激的な論考、ドゥルーズの主要著作ガイドをなどをまとめた魅力的なアンソロジー
『ドゥルーズ――没後20年 新たなる転回』
(河出書房新社編集部編、河出書房新社、2015年10月、本体2,100円、A5判並製272頁)
がまもなく発売されます。
鵜飼さんは宇野邦一さんとの対談「概念の力と「地理哲学」」を寄稿され、
江川さんは堀千晶さんとの対談「絶対的脱領土化の思考」を寄せておられます。
近藤さんは論文「ドゥルーズに影響をあたえた哲学者たち――「プラトニズムの転倒」をめぐる」を、
廣瀬さんは論文「悲劇的なこの世界では哲学が直ちに政治になる。――1969年、スピノザからストア派へ」を寄稿。このほか、
小泉義之さんと千葉雅也さんとの対談「ドゥルーズを忘れることは可能か――20年目の問い」、
檜垣立哉さん、
アンヌ・ソヴァニャルグさん、フランソワ・ズーラビシヴィリさん、
ジャン=クリストフ・ゴダールさん、ペテル=パル・ペルバルトさん、
ローラ=U・マークスさん、ブライアン・マッスミさん、パトリック・ロレッドさん、
李珍景さんらの論考のほか、作家の庄野頼子さんや荻世いをらさんも寄稿されていて、注目です。
西山さんはロレッドの論考「動物は人間のように愚かであることができるか――デリダとドゥルーズをめぐる「超越論的愚かさ」について」を小川歩人さんと共訳されています。デビュー作から遺稿までの著作ガイドのほか、村澤真保呂さんによる「ガタリの著作を読む」、国内外のドゥルーズ論を紹介する堀千晶さんによる「文献案内」が収録されています。堀さんのご紹介によれば来月ミニュイからドゥルーズの『書簡集その他のテクスト Lettres et autres textes』が刊行予定とのことです。書名のリンク先(ミニュイのウェブサイト)で目次をご確認いただけます。》
(河出書房新社編集部編、河出書房新社、2015年10月、本体2,100円、A5判並製272頁)
もくじ
対談
小泉義之×千葉雅也「ドゥルーズを忘れることは可能かーー二○年目の問い」
宇野邦一×鵜飼哲「概念の力と「地理哲学」ーードゥルーズを読みなおすために」
江川隆男×堀千昌「絶対的脱領土化の思考」
文学者が読むドゥルーズ
笙野頼子「すべての隙間にあり、隙間そのものであり、境界をも晦ます、千の内在」
萩世いをら「参照点のない読書」
檜垣立哉「ドゥルーズ没後二○年の〈世界的現在〉」
近藤和敬「ドゥルーズに影響をあたえた哲学者たちーー「プラトニズムの転倒」をめぐる」
アンヌ・ソヴァニャルグ「リゾームと線」 訳=小倉拓也+福尾匠
フランソワ・ズーラビシヴィリ「カントとマゾッホ」 訳=小谷弥生
ジャン=クリストフ・ゴダール「1960年という瞬時におけるドゥルーズーー思考の新たなイマージュ?」 訳=小林卓也
ペテル=パル・ペルバルト「主体化、非主体化」 訳=五井健太郎
ローラ=U・マークス「ドゥルーズ哲学へのモッラー・サドラーの潜在的な貢献」 訳=森元斎
ブライアン・マッスミ「非人間的回転」 訳=黒木秀房
パトリック・ロレッド「動物は人間のように愚かであることができるかーーデリダとドゥルーズをめぐる「超越論的愚かさ」について」 訳=西山雄二+小川歩人
李珍景「ドゥルーズの唯物論、あるいは「外部による思惟」」 訳=影本剛
廣瀬純「悲劇的なこの世界では哲学が直ちに政治になる。ーー一九六九年、スピノザからストア派へ」
・主要著作ガイド
『哲学の教科書』『経験論と主体性』『ニーチェと哲学』『カントの批判哲学』『プルーストとシーニュ』『ベルクソンの哲学』『ザッヒェル=マゾッホ紹介』『差異と反復』『スピノザと表現の問題』『スピノザ』『意味の論理学』『アンチ・オイディプス』『カフカ』『ディアローグ』『重合』『千のプラトー』『フランシス・ベーコン』『シネマ1 運動イメージ』『シネマ2 時間イメージ』『フーコー』『襞』『ベリクレスとヴェルディ』『記号と事件』『哲学とは何か』『消尽したもの』『批評と臨床』『無人島とその他のテクスト』『狂人の二つの体制』
http://www.amazon.co.jp/dp/4309247350/
_____
https://en.wikipedia.org/wiki/Andrey_Markov
Andrey (Andrei) Andreyevich Markov (Russian: Андре́й Андре́евич Ма́рков, in older works also spelled Markoff) (14 June 1856 N.S. – 20 July 1922) was a Russian mathematician.
_____
https://ja.wikipedia.org/wiki/%E3%83%9E%E3%83%AB%E3%82%B3%E3%83%95%E9%80%A3%E9%8E%96
クロード・シャノンが情報理論を創始した論文"A mathematical theory of communication"では、マルコフ連鎖を利用してエントロピーの概念を導入している。
ドゥルーズ、ソヴァニャルグを読んでも実はマルコフ連鎖(離散的というところが重要
だろう)についてはよくわからないので、
以下参考:
マルコフ連鎖とは?
http://mathtrain.jp/markovchain
未来の状態(の確率)が過去の状態によらず現在の状態のみで決まるような確率過程の
ことをマルコフ過程と言います。…特に,確率変数がとりうる値の集合(状態空間)が
離散的なマルコフ過程のことをマルコフ連鎖と言います。
マルコフ連鎖の具体例:
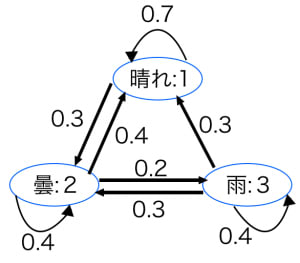
昨日以前の天気は翌日の天気に影響しない。
今日晴れ→翌日晴れる確率は0.7,曇の確率は0.3,雨の確率は0
今日曇→翌日晴れる確率は0.4,曇の確率は0.4,雨の確率は0.2
今日雨→翌日晴れる確率は0.3,曇の確率は0.3,雨の確率は0.4
0.7
↙︎⤴︎
【晴れ:1】
/↗︎ ↖︎
0.3//0.4 \0.3
↙︎/ \
↙︎⤴︎ 【曇:2】 ーー0.2ー→【雨:3】↙︎⤴︎
0.4 ←ー0.3ーー 0.4
P=曇り〈 0.4 0.4 0.2 〉
雨 \0.3 0.3 0.4/
- 推移確率行列の各要素は
0 以上1 以下である。 - 推移確率行列のどの行も,行和は
1 である。
- 有限なマルコフ連鎖
状態の個数が有限(finite)なマルコフ連鎖. - マルコフ性
現在(時刻n)の状態iを知っているときの未来の状態についての偶然法則は,過去の状態に関する情報が得られていても変わらない性質. - 斉時的
推移確率がマルコフ連鎖の位置によらない.… - 既約
任意の状態から別の任意の状態に推移できる確率が常に正である.(どの状態からはじめても到達できない状態がない)… - マルコフ連鎖の周期
有限マルコフ連鎖において,同値関係(ロ )による同値類の中に閉じているものがある.これをE(エルゴード類)として表す.…
つまり,一意な定常分布(stationary distribution)p(x)を有する.
問題点とその解決:MCMCの導入
ベイジアン計量経済学は、常にベイズの定理を適用し、条件付確率を用いた議論を行うという点で一貫性を有している。しかしながら、少しでも分布が複雑になってしまうと、事後分布を解析的に導出することが不可能になるケースが多い。また、仮に導出できたとしても、今度は数値計算が難しくなってしまうという問題がある。このため、これまで計量経済学においてベイズ分析は少なかった。
_____
https://store.toyokeizai.net/books/9784492313398/
ベイズ計量経済分析
和合肇編著 東洋経済新報社
ISBN:9784492313398旧ISBN:4492313397サイズ:A5判 上製 408頁 C3033
発行日:2005年05月20日 【在庫切れ】定価4,968円(税込)
事後分布のシミュレーションを用いる「マルコフ連鎖モンテカルロ法(MCMC)」の利用方法を、理論解説から、経済・金融・ファイナンスなどの実証分析などの応用に至るまで学ぶ1冊
第1章 計量経済分析へのベイズ統計学の応用
第2章 マルコフ連鎖モンテカルロ法とその応用
第3章 アジア金融危機後の外国為替間の関係
(単位根、共和分、VAR)
第4章 マーケットシェアの予測とブランド競合分析
:マーケティング戦略の意思決定
第5章 景気動向指数の継続時間分析
第6章 経済成長の収束仮説
:隠れマルコフ・モデルによる検証
第7章 実質為替レートの中期予測におけるモデルの不確実性
第8章 ディリクレ過程事前分布を用いた構造変化のベイズ分析
第9章 マルチ・ムーブ・サンプラーを用いた
確率的ボラティリティ変動モデルのベイズ推定法
第10章 金融派生証券の価格付けとMCMC
第11章 動学的分布混合モデルを用いた構造変化の分析
第12章 マルコフ・スイッチングを含む
確率的ボラティリティ変動モデル
________
マルコフ連鎖は、計量経済学(econometrics)より統計学および計算物理学で使われる概念らしい。
マルコフ連鎖モンテカルロ法の最近の展開. 大森裕浩 2001
http://www.omori.e.u-tokyo.ac.jp/MCMC/mcmc.pdf
マルコフ連鎖モンテカルロ法
https://ja.wikipedia.org/wiki/%E3%83%9E%E3%83%AB%E3%82%B3%E3%83%95%E9%80%A3%E9%8
研究報告書 補足資料(SA)
青井 桂子
2001年 06月19日
1 マルコフ連鎖
偶然的原因の影響を受けて時間の経過にしたがって状態が変動していくシステムを考える.現在までの状態の経過を知っているときの未来の状態に関する偶然法則が,過去の経過には無関係で現在の時点の状態にのみ依存しているといった場合も少なくない.例えばブラウン運動において,現在までの粒子の経路がわかっているときの"1秒後に粒子が範囲A内にある"確率は,現時点の位置のみに依存していて過去の経路には無関係であると考えられている. と任意の状態
と任意の状態 に対して
に対して | (1) |
が成り立つ時,
 すなわち
すなわち を(S上の)マルコフ連鎖という.
を(S上の)マルコフ連鎖という.- 有限なマルコフ連鎖
状態の個数が有限(finite)なマルコフ連鎖. - マルコフ性
現在(時刻n)の状態iを知っているときの未来の状態についての偶然法則は,過去の状態に関する情報が得られていても変わらない性質. - 斉時的
推移確率がマルコフ連鎖の位置によらない.Fig:2 では状態数3で各々の状態遷移確率(=推移確率)が1/3の等確率推移を行うものである.Figure 2: 斉時的なマルコフ連鎖 - 既約
任意の状態から別の任意の状態に推移できる確率が常に正である.(どの状態からはじめても到達できない状態がない)Figure 3: 既約なマルコフ連鎖Figure 4: 過渡状態のあるマルコフ連鎖Fig:4 では状態 から
から への推移確率が正でないため,状態
への推移確率が正でないため,状態 からは
からは に到達することができない.
に到達することができない. - マルコフ連鎖の周期
有限マルコフ連鎖において,同値関係(ロ )による同値類の中に閉じているものがある.これをE(エルゴード類)として表す.このEの中で更に状態の分類を行う.自然数の集合
(2)
は空ではない.
実際, は
は となるj ホ
となるj ホ  と
と となる
となる とが存在し,
とが存在し, がわかる.Tiに属する自然数の最大公約数diを状態iの周期という. 各状態が周期1を持つつまり,Eの周期が1(d=1)のとき,Eは非周期的であるという.
がわかる.Tiに属する自然数の最大公約数diを状態iの周期という. 各状態が周期1を持つつまり,Eの周期が1(d=1)のとき,Eは非周期的であるという.
2 SAの基礎理論
SAの理論はマルコフ連鎖(Markov chain)理論を用いて,構築できる. | (3) |
更に,生成された状態x「が温度Tkで受理される確率Ax,x「Tkは式(4)で与えられる.
 | (4) |
式(3),(4)より温度Tkにおける推移確率は以下のようになる.
 | (5) |
つまり,一意な定常分布(stationary distribution)p(x)を有する.
 | (6) |
このとき,n(x)は試行回数である.これを∞に近づけることで,平衡分布を得る. ここで,Px,x「は状態x「から状態xへの推移確率を表す.
 | (7) |
更に個別つりあい(detailed balance)の条件(式(8))を満たす時,条件に現れる分布p(x)は定常分布そのものを与える.
 | (8) |
SAでは,各温度で平衡状態が実現されるまで十分な探索(生成→受理判定→推移の一連の処理)を行う.ここで平衡状態とは,各状態xの生起確率が以下のBoltzmann-Gibbs分布(式(9))で与えられるような状態を言う.
 |  | (9) |
a 」 0の時次のことが成り立つ.
 | (10) |
 | (11) |
Reference
- 中野 良平,Bruce E.Rosen シミュレーテッドアニーリング, 人工知能学会誌Vol.9,No.3, 1994
マルコフ過程,マルコフ連鎖とは
マルコフ連鎖の具体例
- 昨日以前の天気は翌日の天気に影響しない。
- 今日晴れ→翌日晴れる確率は
0.7 ,曇の確率は0.3 ,雨の確率は0 - 今日曇→翌日晴れる確率は
0.4 ,曇の確率は0.4 ,雨の確率は0.2 - 今日雨→翌日晴れる確率は
0.3 ,曇の確率は0.3 ,雨の確率は0.4
↙︎⤴︎
【晴れ:1】
/↗︎ ↖︎
0.3//0.4 \0.3
↙︎/ \
↙︎⤴︎ 【曇:2】 ーー0.2ー→【雨:3】↙︎⤴︎
0.4 ←ー0.3ーー 0.4
状態空間は
と書くことができます。
推移確率行列
- 推移確率行列の各要素は
0 以上1 以下である。 - 推移確率行列のどの行も,行和は
1 である。
最後に「推移確率行列のn乗」と「n回の遷移の確率」が対応することを説明します。
n時刻経過に対する推移確率行列をP(n)と書くことにします。つまり,P(Xt+n=j∣Xt=i)をij成分に持つ行列をP(n)とします。
すると,P(n)=Pnが成立します(右辺は推移確率行列のn乗)。
証明
n=1:定義よりP(1)=P
n=2:時刻t+1での状態で場合分けしてt→t+2への遷移確率を計算する。Pのij成分をpijと書く。
_____________
次の状態遷移図で表されるマルコフ連鎖の推移行列はどうなるでしょうか?

答えは,
 = = |
 |
です.
これは,行方向に足すと1になっていますので,確率行列,推移行列になっています.
今,状態遷移図が,下記のようになっているとします.

このように状態が2つ以上のグループに分けられて互いに互いの遷移が無い,というケースが考えられますが,こうならない時,つまり分かれていない時は,過程は「エルゴード(ergodic)的」である,といいます.
分かれている時,過程は「非エルゴード(non ergodic)的」といいます.
ergodicは熱力学の用語です.
今,時点
 での周辺分布が
での周辺分布が とします.
とします.そして,これが定常とします.つまり
 ということです(初期分布を(
ということです(初期分布を(今,1人の人をAさんとします.Aさんの段目を記録します.
Aさんが時点1では1段目,時点2では2段目,時点3では1段目, 時点4では2段目,時点5では3段目,時点6では4段目,というように記録していきます.
 :
:
そして,この記録を,
 とします.
とします.この
 が
時点
が
時点 でのAさんの段目とします.
でのAさんの段目とします.例えば,Aさんが3段目にいた時間的割合はどのようになるかといいますと,
時点
 までの場合を考えるとすると,
までの場合を考えるとすると,
となります.
定理:ほとんど全ての
 …
… は
3段目にいる事象を意味します.
は
3段目にいる事象を意味します.となります.”殆ど全て”という意味は,成立する確率が1ということです.
エルゴード的で無い場合はこのようなことはいえません.
例えば1段目と2段目間しか行き来できず,3段目と4段目の間しか行き来できないとします(下図5,6,7,8段目も同様とする).

(
しかし,たまたまAさんが1段目にいたとすると,絶対に3段目には行けませんので,1段目と2段目で
 ずつの周辺分布しか持てません.
ずつの周辺分布しか持てません.割合で行くと,Aさんにとっては,

となります.
しかし,Bさんにとっては,たまたま3に居たら,

ということになります.
ところで初期分布から考えて

となります.
このように,AさんとBさんの選び方によって,違う値になってしまいます.
___________
http://search.yahoo.co.jp/search?p=%E3%83%AA%E3%83%A5%E3%82%A4%E3%82%A8+%E3%83%9E%E3%83%AB%E3%82%B3%E3%83%95&ei=UTF-8&fr=applpd
Title ドゥルーズの言語論における連鎖と時間性 ... - Osaka University(Adobe PDF) -htmlで見る
http://ir.library.osaka-u.ac.jp/dspace/bitstream/11094/7249/1/ahs32_119.pdf
〈論文〉 ドゥルーズの言語論における連鎖と時間性 130頁
このように、カオスから懸隔を保ちかっ言葉の創造性を保つという ドゥルーズ H ラカン的な賭け金、か、「文法」「統語法」という観点から明 らかになった。以上から、ドゥルーズ=ラカン的な言語論を「マルコフ連鎖」として正確に規定することができる。
一般に、言語論における「マルコフ連鎖」は、次のように定義され る。それは、記号の連鎖において、パラディグマ的な選択とシン夕、グマ 的な位置どりという二つの軸を結合させることによって、位置から位置 (9) へと文の表面構造を生みだしていく「統語法的機械」のことである。そ れはまた、英米系の認知言語学、 コンピュータ言語学においても、確率 過程のシミュレーションとして採用されている。そして「マルコフ連 鎖」の特徴は、①線的である、②偶然的である、③部分的に依存的であ (ω) る、と規定される。線形性については連鎖という観点、か、偶然性と部分 的依存性については、 いかなる連鎖であれそれが規則を保つのであれば 意味を生みだすという観点が、それぞれ、われわれが見てきたドゥルーズ =ラカン的な言語論と一致している。また、 マルコフ連鎖が可能性の 漸進的な限定によってことにあたる確率過程であるということは、われ われの「遡及的な論理的時間」と一致する。ルセルクルは、クッション の綴じ自によって区切られて遡及的・事後的に意味が生産されるラカン 的なマルコフ連鎖を、「統語法の強度内包的線[E ロ宮町一三 g 号一 OR 同町宮 (日) 回百 S5] 」と呼び、それによってドゥルーズの言語論を特徴づけている。 「マルコフ連鎖」として捉えられた言語は、その統語的進展における 偶然性ゆえに、その都度無意識や欲望や情動が介入し、遡及的な時間性 ゆえに、あらかじめ決まったものとしてではなく聞かれたものとして意 味を規定し、またその部分的依存性にゆえにカオスに陥ることなく、創 造的な意味を生むのである。機知やユーモアは、言葉のこうしたシステ ムの効果、たといえる。ここにおいて、もはや体系性や規則性と、それを 侵犯する作用とが対立させられることはない。それらは原理上分かちが たく相互に折り込まれているのである。われわれが、言語の構造と発生 が、決して既存の上位の形式性に従属していくプロセスではないと強調 したのも、このことを指している。それは、連鎖のその都度に意味、か変 化していくようなシステムなのである。これが「マルコフ連鎖」として 捉えられるドゥル l ズ H ラカン的な言語論の最も肯定的な側面だといえ るだろう
____________
ヴイツチ・マルコフによって理論化されたものである。 一九七〇年代以降のドゥルーズは、それをもっぱらレ. 1. モン・リュイエから借用し、生. 命や社会に適用している。 ドゥルーズにとって「マルコフ連鎖」が重要. なのは、それが「決定された ...
書評 - Osaka University (Adobe PDF) -htmlで見る
http://ir.library.osaka-u.ac.jp/dspace/bitstream/11094/24966/1/ahs34_247.pdf
ドゥルーズとガタリは、このようなマルコフ連鎖をモデルに機械的コード化を定式化する ことによって、. 意味作用とは無関係 ... ソヴァニャルグはこのような記号のプロセスを「開 かれた形態化」というリュイエの言い回しで形容し、. 第 8 章と第 9 章 ...
Title ジル・ドゥルーズの哲学における意味と感覚の ... - 大阪大学リポジトリ(Adobe PDF) -htmlで見る
http://ir.library.osaka-u.ac.jp/dspace/bitstream/11094/54017/2/27855_%E8%AB%96%E6%96%87.pdf 博論 小倉拓也
《私は点というものが好きになれないし、定点をさだめる(ポイントをおさえる)ことは愚劣だ
と考えています。ふたつの点のあいだに線があるのではなく、線が何本も交差したところに
点があるわけですからね。》
(ドゥルーズ『記号と事件』より)
___________________
投資が利子率に依存するときの投資需要の増加:
利|
子|
率|投資曲線 \ S(r)貯蓄
| \ \/
⬆︎| \ /\
| \/➡︎ \
| /\ \
| _/ I1 I2
|________________
投資・貯蓄
上の図では、利子率が高くなると⬆︎、人々は貯蓄を増やすように促され➡︎、それなりに投資も増えることが出来る➡︎。
つまり、利子率が上昇⬆︎したときに人々が消費を減らして貯蓄を増やすと➡︎、正の相関が起こる↗︎。
S(r)が垂直↕︎なら投資需要が増加すると、貯蓄量は一定つまり均衡投資量(一部ではなく貯蓄全体)は不変で、投資量のみ増えることもあり得る➡︎。
とはいえ、基本的には利子率が高くなると⬆︎それにみあった投資が少なくなり⬅︎、貯蓄が増える➡︎。
(マンキューマクロ入門篇邦訳第二版3-12:88~9頁参照)
ただし、生じていること(複数の線)と観察されること(複数の点)は違う。(同91頁)
参考図:
生じていること(複数の線)と観察されること(複数の点)
(マンキューマクロ入門篇邦訳第二版3-12:91頁)
生じていること(複数の線):
r|
| S1
| \/
| /\ S2
| \/ \/
| /\ /\ S3
|\/ \/ \/
|/\ /\ /\I3
| \/ \/
| /\ /\I2
| \/
| /\I1
|_____________
I,S
観察されること(複数の点):
r|
|
| 。
|
| 。 。
|
| 。 。 。
|
| 。 。
|
| 。
|
|_____________
I,S
I:投資、S:貯蓄、r:利子率
__________________
マルコフ連鎖が意味するものはドゥルーズにとって、まずはその自由間接話法的な記述形式であろう。
ドゥルーズはむろん資本主義に否定的だが、なぜか近代経済学(死語?主流派経済学と呼ぶべきか) と相性がいい。その欲望の哲学は功利主義ではなく枠組みの延命を許さない種類のそれだ。資本主義を徹底することで資本主義を超える。
http://www.amazon.co.jp/dp/4876989621
「貨幣について」1752
http://www.eonet.ne.jp/~bookman/zenkotennha/hume.html
《この現象を説明するためには、われわれはつぎのことを考察しなければならない。すなわち、財貨の高価格は、金銀の増加の必然的結果であるけれども、しかしこの増加につづいてただちに生じるものではなく、貨幣が国家の全体に流通し、その影響がすべての階級の人びとに及ぶまでには、いくらかの時間が必要である。最初は、何らの変化も感じられないが、まず一つの財貨から他の財貨へと次第に価格が騰貴して行き、ついにはすべての財貨の価格がこの国にある貴金属の新しい量ちょうど比例する点に到達する。私の意見では、金銀の量の増加が勤労にとって有利なのは、貨幣の獲得と物価の騰貴との間の間隙、あるいは中間状態においてだけである…》(同p.42)。《貨幣が国家全体を流れていくのを巡ることはたやすい。その場合、貨幣は労働の価格を騰貴させるよりも前に、まずあらゆる個人の勤労を増大させるにちがいない。》(同p.46)。
(マンキュー邦訳第3版入門編1:3:7,281頁、邦訳第2版応用編2:3:8,256頁参照。『市民の国について (下) 』57~8頁(岩波文庫.ヒューム, 小松 茂夫)参照。)
なおA.O(1972)に続いて『フーコー』(1986)にもダイアグラムと関連してマルコフ連鎖について言及がある。
Foucault (1986)『フーコー』 宇野邦一訳、河出書房新社、1987/河出文庫、2007
http://www.amazon.co.jp/dp/4309462944
フーコー (河出文庫) [文庫] ジル ドゥルーズ (著), Gilles Deleuze (原著), 宇野 邦一 (翻訳)
文庫: 196ページ
出版社: 河出書房新社 (2014/12/8)
目次:
古文書からダイアグラムへ
新しい古文書学者―『知の考古学』
新しい地図作成者―『監獄の誕生』
トポロジー、「別の仕方で考えること」
地層あるいは歴史的形成物、可視的なものと言表可能なもの―知
戦略あるいは地層化されないもの、外の思考―権力 ☆
褶曲あるいは思考の内―主体化
付記―人間の死と超人について
Gilles Deleuze
Foucault 1986 144 pages Minuit
http://www.leseditionsdeminuit.fr/f/flip.php?editor=3&livre_id=2019
Foucault
Couverture 1
Du même auteur 4
Titre 5
Copyright 6
Avant-propos 7
DE L’ARCHIVE AU DIAGRAMME 9
Un nouvel archiviste (L’Archéologie du savoir) 11
Un nouveau cartographe (Surveiller et punir) 31
TOPOLOGIE : « PENSER AUTREMENT » 53
Les strates ou formations historiques : le visible et l’énonçable (savoir) 55
Les stratégies ou le non-stratifié : la pensée du dehors (pouvoir) 77 ☆
Les plissements, ou le dedans de la pensée (subjectivation) 101
ANNEXE. Sur la mort de l’homme et le surhomme 131
I. – LA FORMATION HISTORIQUE « CLASSIQUE » 131
II. – LA FORMATION HISTORIQUE DU XIXe SIÈCLE 134
III. – VERS UNE FORMATION DE L’AVENIR ? 138
Table des matières 142
Justification 144
《何でもかんでもが互いに連鎖するということではない。重要なのはむしろくじびきの連鎖であり、各くじびきは、マルコフ連鎖におけるように…、偶然に、しかし先行するくじびきによって決定された外因性の諸条件のなかで、振る舞う。…それゆえ連続性による連鎖も内面化もなく、ただ諸々の切断と不連続性(変異)を越えていく再連鎖がある。》p.92,邦訳文庫159頁
半偶然性、半偶発的連鎖......柄谷行人の言う選挙+くじ引きみたいなものか?
DRは強度を外から捉えていて、LSは意味を内部から捉える。*
AOは社会に留まり、MPは飛び立つ。
Foucaultは基礎となるダイアグラムを準備する。
懐疑論はHumeにある。
アプリオリな総合はLeibnizにある。
Bergson的な時間とともにシーニュはProustにある。
Nietzsche、Spinozaはこれらを横断する。
Cinemaは狂気の断絶を系譜、系列として歴史化する。
A
F O H
DR + LS
L M B
P
分
析
規定 + 反省
総
合
A
F O H
DR C LS
L M B
P
*
宇野邦一《「意味」は『差異と反復』のどこにあるのか。
「強度」は『意味の論理学』のどこに行ったのか。》(没後~120頁)。
|
\ A /
F\O/H
ーDRーーCーーLSー
L/M\B
/ P \
|
分
析
規定 + 反省
総
合
参考:
プルースト:メモ(下書き)
http://nam-students.blogspot.jp/2015/10/blog-post_30.html
DRは強度を外から捉えていて、LSは意味を内部から捉える。*
AOは社会に留まり、MPは飛び立つ。
Foucaultは基礎となるダイアグラムを準備する。
懐疑論はHumeにある。
アプリオリな総合はLeibnizにある。
Bergson的な時間とともにシーニュはProustにある。
Nietzsche、Spinozaはこれらを横断する。
Cinemaは狂気の断絶を系譜、系列として歴史化する。
|
\ A /
F\O/H
ーDRーーCーーLSー
L/M\B
/ P \
|
分
析
規定 + 反省
総
合
*《「意味」は『差異と反復』のどこにあるのか。「強度」は『意味の論理学』の
どこに行ったのか。》宇野邦一(『没後~』120頁)。
_________
DRは強度を外から捉えていて、LSは意味を内部から捉える。*
AOは社会に留まり、MPは飛び立つ。
Foucaultは基礎となるダイアグラムを準備する。
懐疑論はHumeにある。
アプリオリな総合はLeibnizにある。
Bergson的な時間とともにシーニュはProustにある。
Nietzsche、Spinozaはこれらを横断する。
Cinemaは狂気の断絶を系譜、系列として歴史化する。
|
( 分 析 )
\ アンチ /
オイディプス/
フーコー \ | /ヒューム
\|/
(規定)差異と反復ーーーシネマーーー意味の論理学(反省)
/|\
ライプニッツ | \ベルグソン
/千のプラトー
/( 総 合 )\
|
これらはカント体系()とずれながらも一致していると考えていい。
*
《「意味」は『差異と反復』のどこにあるのか。「強度」は『意味の論理学』の
どこに行ったのか。》(宇野邦一『没後~』120頁)。
AOは社会に留まり、MPは飛び立つ。
Foucaultは基礎となるダイアグラムを準備する。
懐疑論はHumeにある。
アプリオリな総合はLeibnizにある。
Bergson的な時間とともにシーニュはProustにある。
Nietzsche、Spinozaはこれらを横断する。
Cinemaは狂気の断絶(1945,1968)を系譜、系列として歴史化する。
【 分 析 】
\ アンチ /
オイディプス/
フーコー \ | /ヒューム
\|/
【規定】差異と反復ーーーシネマーーー意味の論理学【反省】
/|\ (修辞学?)
ライプニッツ | \ベルグソン
/千のプラトー
/【 総 合 】\
これらはカント体系【 】とずれながらも一致していると考えていい。
*《「意味」は『差異と反復』のどこにあるのか。「強度」は『意味の論理学』の
どこに行ったのか。》(宇野邦一『没後~』120頁)。
「意味の論理学」ではなく「意味の修辞学」とすべきだ。









2012 年度応用マクロ経済学講義ノート
マルコフチェーン
阿部修人
平成 24 年 6 月 17 日
概 要 1
マルコフチェーンの性質
不確実性下の経済行動を描写するとき、確率現象をモデルに導入すること になる。ミクロ経済学の初歩で扱われる確率現象は、例えば降水確率や交通 事故にあう確率、等、一回限りの不確実性であることが多く、静学モデルで 分析することが念頭に置かれている。しかしながら、動学モデルの場合は、 今期の確率変数のとる値やその確率が前期の様子に依存すると仮定すること ができる。例えば、確率変数として、ある人間の雇用状態を考え、雇用と失 業の二種類の状態をとると考えよう。最も単純な仮定としては、来期雇用さ れるか否かは前期の雇用状態に依存しないとするものであるが、これは極め て非現実的である。前期失業している者は今期も失業する確率は高いし、前 期雇用されている者は今期も継続して雇用される確率は高いと考えるのが普 通であろうし、実際に多くの実証研究で支持されている。このような前期の 状態に今期の状態確率が依存する状態を描写するときに、最も単純な確率過 程がマルコフチェーンである。
動学モデルの数値解析において、マルコフチェーンの果たす役割は大きい。 不確実性のない、単純なマクロモデルでは、今期の資本ストックが所与の時、 来季の資本ストックがどこに行くのが最適であるかを Policy Function で表 した。これは、各行に関して、要素 1 が一つだけ入る特殊なマルコフチェー ンとみなすことができる。経済に不確実性が導入されると、より多くの non zero 成分を含むマルコフチェーンとして Policy Function が導出されること になる。
一般に、マルコフ過程とは、二つの時間 t 1 と t 2 ( t 1 < t 2 ) が与えられた時、 t = t 1 における状態、例えば C ( t 1 ) の実現値のみによって、確率変数 C ( t 2 ) の分布が決まり、時刻 t 1 よりも前の歴史には無関係の場合、 C ( t ) をマルコ フ過程という。未来は現在のみに依存し、過去には関係しない、ということ である。現在の状態に、それまでの歴史的情報が全て含まれており、現在の 状態が将来を決定するという考えは、 Dynamic Programing と親和的であり、 前述のように、 Policy Function を経由した、状態の遷移式はマルコフ過程の 一種とみなすことができるのである。
現在失業しているとき、来季に就業する確率が 0.4 、現在就業していて、将 来失業する確率が 0.1 だとする。すると、機械的に、現在失業していて、来 季も失業し続ける確率は 0.6 で、現在就業していて、来季も就業し続ける確 率は 0.1 となることがわかる。