∞?
虚部 |
| |
| |
_______|_|___
ー1 0| | 1 実部
| |
| |
1/2
>素数の研究の関連で特定の方程式が出て(素数自体の導出式イコールではない)、
>その式( x何ちゃら=0 になるxの値) の解はxが複素数だとたくさんあるところ、
>全部 x= 0.5 + t*i (tはいろんな値、iは虚数)になるだろう、ということ
>x= 0.35+ 23i とか、 101+5.6i とかになることは絶対になく、
>0.5+?i というふうに0.5だけ
ゼータ関数:
y=1/x^s
y| 。
| |。
| | 。
| | | 。
_|_|__|__|__|__
0 1 2 3 4 x
Re(s)>1 の場合、
1+(1/2^s)+(1/3^s)+(1/4^s)+(1/5^s)+(1/6^s)+・・・・・
(sは複素数)
の形をゼータ関数という
http://anago.2ch.net/test/read.cgi/scienceplus/1447825632/
【数学】イーノック教授「リーマン予想を解いた」と主張 ©2ch.net
17 :名無しのひみつ@転載は禁止:2015/11/18(水) 15:12:34.88 ID:/eaZ7taW
>>10
素数が出てくる規則を求める式をリーマンが考えた
この式が正しいことを証明すれば解決
で、OK? 数学に詳しい人確認して
71 :名無しのひみつ@転載は禁止:2015/11/18(水) 18:39:35.70 ID:B+SF11iA
>>17
ちょっと違うだろうな
ウィキに書いてあるとおりだが、素数の研究の関連で特定の方程式が出て(素数自体の導出式イコールではない)、
その式( x何ちゃら=0 になるxの値) の解はxが複素数だとたくさんあるところ、
全部 x= 0.5 + t*i (tはいろんな値、iは虚数)になるだろう、ということ (ベタに数値実験するとそうなる)
x= 0.35+ 23i とか、 101+5.6i とかになることは絶対になく、 0.5+?i というふうに0.5だけ
式の形からして、左のようないろいろ乱雑なものになっても全然よさそうなところ、0.5に統一される、というところの不思議
しかしその証明が天才数学者総がかりで一世紀半解けない
現代数学最先端の数論幾何、グロタンディークとか望月教授の分野も、ある面いずれそれを解くことを横目でにらみながら、物凄い高難度抽象システムを延々作り上げて来たといっていいほど
146 :名無しのひみつ@転載は禁止:2015/11/19(木) 20:49:25.55 ID:1FyUb5R1
その前に
1+(1/2^s)+(1/3^s)+(1/4^s)+(1/5^s)+(1/6^s)+・・・・・
(sは複素数)
の形をゼータ関数という、という辺りから
スレ内で説明した方が良いんじゃないかなあ?
いきなり素数の話になって
そこから更にSSL認証通信のRSA暗号が全部丸見えだぜ~って話になってもなあ
196 :名無しのひみつ@転載は禁止:2015/11/22(日) 08:58:45.45 ID:be4xJHc5
>>193
ゼータ関数が
ζ(s) = 1^(-s) + 2^(-s) + 3^(-s) + …
と書けるのは Re(s)>1 の場合のみよ。
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1136066801
oga4930さん
2010/1/3116:11:10
数学に興味があるので、詳しく教えてください。
他にもいろいろ教えてください。
中3でも分かりやすくお願いします。多少難しくてもいいです。
他にもいろいろ教えてください。
中3でも分かりやすくお願いします。多少難しくてもいいです。
xy平面(普通の座標平面)を書いてみてください。
このグラフ上で、
x=0以外では、y=0
x=0のところだけでは、yはどこまでも大きくなる
という関数が、ゼータ関数です。
x=0のところで、yがどこまでも大きい、というのは、その平面状の、すべてのxの範囲での積分という操作をすると、面積が1になる、ということなのですが、どういうことか、おおよその説明をします。
(範囲が決まっている)積分、というのは、(定積分と呼びますが)簡単に言えば、x軸とその関数のグラフとの間にはさまれている面積を求める、ということ です。もちろん、面積、ということは、直線とか曲線とかで全方向を囲まれていなければ決まらないので、左と右の端を決めます。つまり、ある関数のグラフ (y=x^2とか)と、x軸との間で囲まれた部分の、ある範囲(x=3からx=6までの間とか)の面積を求めることを、(x=3からx=6の範囲で)積分 する、と呼ぶわけです。
このとき、横の範囲は、考えているのですが、限りなく左にある左端から、限りなく右にある右端までの範囲で積分する(つまり、その平面全体での面積を求める)と、ゼータ関数は、その値が1になります。
普通、長方形の面積って、横の長さ×縦の長さで求めますよね。
しかし、ゼータ関数というのは、はじめに言ったとおり、x=0のときだけ値が0より大きいので、横の長さがありません。というか、横の長さは0で、縦の長 さが?の長方形の面積と同じだと思えるわけですね。だから、縦の長さはいくら大きくても足りませんが、いくらでも大きければ、面積が出てくるんじゃない か、という風に思うわけです。(実際は、もっと厳密に考えるのですが、おおよそのイメージとしてはこんな感じです)。
あと、その使い道ですが、
関数f(x)に、ζ(x)をかけて、x=-∞からx=∞の範囲で積分すると、f(0)の値が出てきますね。なぜかというと、ζ(ゼータと読む)関数は、積分した時、x=0のときだけ面積が1になるからです。
という使い方ができます。
このグラフ上で、
x=0以外では、y=0
x=0のところだけでは、yはどこまでも大きくなる
という関数が、ゼータ関数です。
x=0のところで、yがどこまでも大きい、というのは、その平面状の、すべてのxの範囲での積分という操作をすると、面積が1になる、ということなのですが、どういうことか、おおよその説明をします。
(範囲が決まっている)積分、というのは、(定積分と呼びますが)簡単に言えば、x軸とその関数のグラフとの間にはさまれている面積を求める、ということ です。もちろん、面積、ということは、直線とか曲線とかで全方向を囲まれていなければ決まらないので、左と右の端を決めます。つまり、ある関数のグラフ (y=x^2とか)と、x軸との間で囲まれた部分の、ある範囲(x=3からx=6までの間とか)の面積を求めることを、(x=3からx=6の範囲で)積分 する、と呼ぶわけです。
このとき、横の範囲は、考えているのですが、限りなく左にある左端から、限りなく右にある右端までの範囲で積分する(つまり、その平面全体での面積を求める)と、ゼータ関数は、その値が1になります。
普通、長方形の面積って、横の長さ×縦の長さで求めますよね。
しかし、ゼータ関数というのは、はじめに言ったとおり、x=0のときだけ値が0より大きいので、横の長さがありません。というか、横の長さは0で、縦の長 さが?の長方形の面積と同じだと思えるわけですね。だから、縦の長さはいくら大きくても足りませんが、いくらでも大きければ、面積が出てくるんじゃない か、という風に思うわけです。(実際は、もっと厳密に考えるのですが、おおよそのイメージとしてはこんな感じです)。
あと、その使い道ですが、
関数f(x)に、ζ(x)をかけて、x=-∞からx=∞の範囲で積分すると、f(0)の値が出てきますね。なぜかというと、ζ(ゼータと読む)関数は、積分した時、x=0のときだけ面積が1になるからです。
という使い方ができます。
リーマン予想の意味
リーマン予想の主張を解説します。- ・ゼータ関数
ζ(z) というのは1 以外の複素数全体で定義された関数です。実部が1 より大きい複素数z に対してはζ(z)=∑n=1∞1nz という美しい式で定義されます。→ゼータ関数の定義と基本的な話 ζ(z)=0 となる複素数z をゼータ関数の零点と言います。ζ(−2)=ζ(−4)=⋯=0 が成立することが(ζ 関数にある程度精通している人にとっては)簡単に分かるので負の偶数は自明な零点と呼ばれます。
以上を踏まえると,リーマン予想は
分かっていること
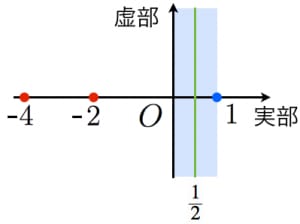
事実2:実部が
事実3:非自明な零点の実部は
素数との関係
このとき,
実は,リーマン予想よりも弱い主張(上記の事実3)を認めるだけで素数定理が比較的容易に証明できます。さらに,リーマン予想が正しいとしたら素数定理の近似精度に関するよりよい理論保証が与えられます。そのような意味でリーマン予想と素数分布は関係しています。
RSA暗号との関係
最後に,リーマン予想と暗号の関係についてです。RSA暗号の安全性の根拠は素因数分解の難しさです。→素因数分解の難しさと素数判定
しかし,リーマン予想が証明されたからと言って大きな数の素因数分解が現実的な計算時間でできるようになる訳ではありません(少なくとも僕の知っている&調べた限りでは)。
正:リーマン予想が証明される→素数分布の性質が(
誤:リーマン予想が証明される→RSA暗号が突破できる(^O^)
NHKスペシャル「魔性の難問 ~リーマン予想・天才たちの闘い~」という番組では上記の「誤」があたかも正しいかのような説明の仕方をしていたので残念でした。
ゼータ関数の定義と基本的な話
ゼータ関数の値の存在
まずは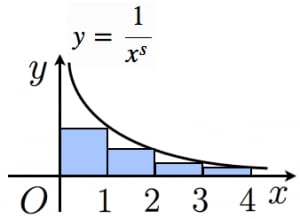
証明
実際に右辺を計算すると,
を得る。よって,
複素数に広げる
実数の複素数乗は定義できる(→複素数の対数関数とiのi乗が実数であること)ので冒頭の式は実際,実部が
すなわち,冒頭の表式を使うことで実部が
しかし,残念ながら実部が
解析接続
ゼータ関数の定義域をさらに広げるためには解析接続という方法を使います。解析接続の詳細はここでは説明しませんが,ざっくり言うと
複素数平面上のある領域で定義された関数を,いい感じに延長して定義域を広げることです。
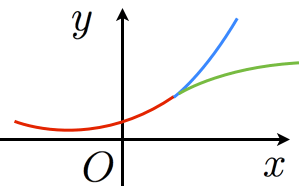
ゼータ関数の解析接続
ゼータ関数はこれでゼータ関数を定義できたのですが「
解析接続をした具体的な式はベルヌーイ数を用いて表す方法や,ガンマ関数を用いて表す方法などがあるようですが,いずれも複雑だったり場合分けが必要だったりします。
ゼータ関数のいくつかの値
・これは平方数の逆数和の話です。→バーゼル問題の初等的な証明
・
・
ゼータ関数に負の偶数を代入すると
リーマン予想についてはそのうち別記事で書きたいなあと思っています。
追記:→リーマン予想の意味,素数分布との関係フーリエ級数展開の公式と意味
フーリエ級数展開:
f(x) が周期T の「まともな」関数なら
f(x)=a02+∑n=1∞(ancos2πnxT+bnsin2πnxT)
ただし,
an=2T∫T0f(x)cos2πnxTdx
bn=2T∫T0f(x)sin2πnxTdx
ただし,
フーリエ展開の意味,係数の導出,応用例として
フーリエ級数展開とは
〜やりたいこと〜与えられた周期
〜なぜ
・
特に,
フーリエ級数展開の条件
冒頭では「まともな」関数と述べてぼかしました。やばい関数だとフーリエ級数展開できませんが,応用上登場する関数はだいたいフーリエ級数展開できるのでそんなに気にしなくてOKです。例えば
フーリエ級数展開できるための詳しい条件については専門書を参照して下さい。
フーリエ係数の導出
フーリエ係数
(係数の導出)
〜a0 について〜
f(x)=a02+∑n=1∞(ancos2πnxT+bnsin2πnxT)
の両辺を0 からT まで積分すると(右辺の周期関数の積分が全て0 になるので),∫T0f(x)dt=a02T
つまり,a0=2T∫T0f(x)dt
〜an (n≥1 )について〜
f(x)=a02+∑n=1∞(ancos2πnxT+bnsin2πnxT)
の両辺にcos2πnxT をかけて0 からT まで積分すると,∫T0f(x)cos2πnxTdx=an2T (→注1)
よりan=2T∫T0f(x)cos2πnxTdx
〜bn について〜
同じように両辺にsin2πnxT をかけて0 からT まで積分するとOK。
注1:三角関数の直交性という積分公式を用いています。→三角関数の積の積分と直交性〜
の両辺を
つまり,
〜
の両辺に
より
〜
同じように両辺に
この公式により右辺の各項の積分はほとんど
注2:なお,積分と無限和の順序交換が可能であることを仮定しています。この部分が厳密ではありませんが,フーリエ係数の形の意味を見るには十分でしょう。
なお,フーリエ展開には複素指数関数を用いた表現もあります。→複素数型のフーリエ級数展開とその導出
具体例
例題
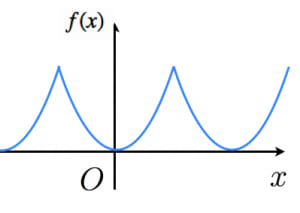
解答
フーリエ係数を求める。周期性に注意するとつまり,
ちなみにこの式に
となり,有名な級数
フーリエ展開を使えば他にもいろいろな級数が導出できます!
調和級数1+1/2+1/3…が発散することの証明
一般的に無限級数の評価は
1,式変形による等式変形,不等式評価
2,積分を用いた不等式評価
のいずれかの方法で行います。この公式の場合はどちらの方法も通用します。2,積分を用いた不等式評価
1:1+1/2+1/3+…を不等式で下からおさえる方法
おそらく一番有名な方法です。エレガントです。証明
この変形を一般化すると,以下の不等式が得られる:
以上から題意は証明された。
2:1+1/2+1/3+…を不等式で下からおさえる方法その2
指数関数の有名不等式Honsbergerによって発見された証明です。
証明
よって,
オイラー定数:γ= limn→∞(∑k=1n1k−log(n+1))= limn→∞(∑k=1n1k−logn)
ただし、最後の等号はより成り立つ。
3:積分を用いた1+1/2+1/3+…の発散証明
無限級数の評価で積分を用いるのは定石です。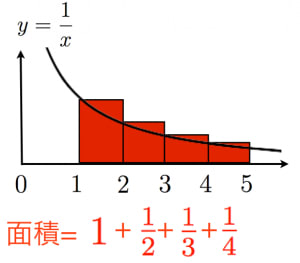
証明
右の図より,となり方法2で導いたものと同じ不等式が得られる。
ちなみに,分数を交互に足し引きして
→log2に収束する交代級数の証明
小学生でも意味が分かる奥深い問題だからこそおもしろい
バーゼル問題の初等的な証明
バーゼル問題:平方数の逆二乗和はπ26 に収束する。つまり,
∑k=1∞1k2=1+14+19+⋯=π26
平方数の逆二乗和はいくつに収束するのか?という問題がバーゼル問題です。高校数学で理解できるバーゼル問題の証明を解説します。級数が収束すること
一般に,バーゼル問題は
まず,この級数が発散せずに収束することは以下のように簡単に証明できます。非常に有名なテクニック:→部分分数分解など差に分解する4つの恒等式を用いて級数を上からおさえます。
証明
バーゼル問題の証明の道具
バーゼル問題の級数の収束先がここでは,大学数学の道具を使わず高校数学で理解できる方法で証明します。
使う道具は以下の3つです:
1:0≤x≤π2 においてsinx≤x≤tanx (有名不等式)
2:(cosθ+isinθ)n=cosnθ+isinnθ (ド・モアブル)
3:解と係数の関係
1についてはsinx/xについて覚えておくべき2つのこと,2:
3:解と係数の関係
2については,ドモアブルの定理の意味と証明を参照して下さい。
バーゼル問題の証明の前半
まずは部分和証明の前半
各辺の逆数をとって二乗すると,
これを変形して平方数の逆数を作り出す:
これを
よって,あとは
証明の後半:東工大の入試問題
目標はこれは,1990年東工大後期第二問と本質的に同じ問題になります。(東工大の入試問題では誘導がついていました。)
ド・モアブルの定理と解と係数の関係を使います!
証明
また,
この
つまり,この
すなわち
実際,二項定理を用いて計算すると,
よって,
思ったより長く険しい証明になってしまいました。
Tag: 無限和,無限積の美しい公式まとめ

0 件のコメント:
コメントを投稿