上田 睆亮(早稲田大・理工 / 理化学研究所)
https://www.jstage.jst.go.jp/article/japannctam/58/0/58_0_3/_pdf
複雑系
https://nam-students.blogspot.com/2019/05/blog-post_30.html
カオス理論
https://nam-students.blogspot.com/2019/04/blog-post_62.html@
スティーヴ・キーン『次なる金融危機』
https://nam-students.blogspot.com/2019/04/can-we-avoid-another-financial-crisis.html
塩沢由典 比較優位
https://nam-students.blogspot.com/2019/04/blog-post_20.html
アトラクター(英: attractor)は、ある力学系がそこに向かって時間発展をする集合のことである。
その力学系において、アトラクターに十分近い点から運動するとき、そのアトラクターに十分近いままであり続ける。アトラクターの形状は点や曲線、多様体、さらにフラクタル構造を持った複雑な集合であるストレンジアトラクターなどをとりうる。
カオスな力学系に対してアトラクターを描写することは、現在においてもカオス理論における一つの研究課題である。
アトラクターに含まれる軌道は、そのアトラクターの内部にとどまり続けること以外に制限はなく、周期的であったり、カオス的であったりする。☆
参考:
Ananalysis of the Keen model for credit expansion, asset price bubbles and financial fragility M. R. Grasselli · B. Costa Lima 2011
https://ms.mcmaster.ca/~grasselli/GrasselliCostaLima_MAFE_online.pdf
^参照
9. Keen, S.: Finance and economic breakdown: modeling Minsky’s “Financial Instability Hypothesis” . J. Post Keynes. Econ. 17(4), 607–635 (1995)
https://keenomics.s3.amazonaws.com/debtdeflation_media/papers/Keen1995FinanceEconomicBreakdown_JPKE_OCRed.pdf
Goodwin関連 http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=S0121-47722010000200001
10. Keen, S.: The nonlinear economics of debt deation. In: Barnett, W.A. (ed.) Commerce, Complexity, and Evolution: Topics in Economics, Finance, Marketing, and Management. Proceedings of the Twelfth International Symposium in Economic Theory and Econometrics, pp. 83–110, Cambridge University Press, New York (2000)
11. Keen, S.: Household debt: the nal stage in an articially extended Ponzi bubble. Aust. Econ. Rev. 42(3), 347–357 (2009)
http://www.rogerfarmer.com/rogerfarmerblog/2016/10/4/nho932exasra0c2a2amkvdmovcy9rz
https://translate.google.com/translate?sl=auto&tl=ja&u=http%3A%2F%2Fwww.rogerfarmer.com%2Frogerfarmerblog%2F2016%2F10%
2F4%2Fnho932exasra0c2a2amkvdmovcy9rz
スティーヴ・キーン『次なる金融危機』
https://nam-students.blogspot.com/2019/04/can-we-avoid-another-financial-crisis.html
リカード『経済学および課税の原理』(On the Principles of Political Economy, and Taxation)
http://nam-students.blogspot.jp/2015/04/on-principles-of-political-economy-and_25.html
http://nam-students.blogspot.com/2013/04/blog-post_0.html
NAMs出版プロジェクト: 価値形態論(逃走論 1984,1986)
https://nam-students.blogspot.com/2019/02/the-fractal-keynesian-stimulus-by-csr.html
カオス理論
https://nam-students.blogspot.com/2019/04/blog-post_62.html@
https://compenn.exblog.jp/438844/
目次
カオスの定義と特性
非線形性
初期値鋭敏性
有界性
非周期性
数学的定義の例
研究史
カオス命名以前
カオス命名と研究の隆盛
カオスの一例
ロジスティック写像
のとき、個体数
はある一定の値に収束する。
のときについては、まず
が3を超えたところで
が2つの値を繰り返す様になる。さらに
が
より大きくなると
のとる値が4つ、8つと増加していく。この周期逓倍点の間隔は一定の比率ファイゲンバウム定数で縮まる。
のとき、
のとる値に規則性が見られなくなる。この境界値3.56995をファイゲンバウム点と呼ぶ。周期逓倍点の間隔が0に収束し、周期が無限大に発散したのであるが、場所によっては3と7の周期性が戻る。この部分は"窓"と呼ばれる。
実際の個体数の変動
カオスの判定
サロゲート法
- 有意水準をαとする
- 元時系列のパワースペクトルを計算
- パワースペクトルを元時系列とし、位相をランダムに設定した新スペクトルをN個作成
- 新スペクトルをフーリエ逆変換して、新時系列をN個作成(これらをサロゲートデータと呼ぶ)
- 元の時系列の統計値<N個の新時系列の統計値の下α/2を与える値 または N個の新時系列の統計値の上α/2を与える値<元の時系列の統計値 → 帰無仮説棄却(ノイズとは言えない)
脚注
注釈
出典
- ^ 下條 1992.
- ^ 早間 2002.
- ^ a b 合原・黒崎・高橋 1999, p. 228.
- ^ 井上 1997, p. 51.
- ^ a b c d 下條 1992, p. 2.
- ^ a b 井上 1997, p. 81.
- ^ 合原 2011, p. 7.
- ^ Devaney 1990, p. 267.
- ^ a b 合原 1990, pp. 14-16.
- ^ 合原・黒崎・高橋 1999, p. 44.
- ^ 合原 1990, p. 1.
- ^ a b 船越 2008, p. 14.
- ^ a b c d アリグッド・サウアー・ヨーク 2012, p. 120.
- ^ a b c d e 井上 1997, p. 56.
- ^ Lorenz 1997, p. 19.
- ^ a b c 森・蔵本 1994, p. 135.
- ^ 井上 1997, p. 54.
- ^ 合原・黒崎・高橋 1999, p. 14.
- ^ アリグッド・サウアー・ヨーク 2012.
- ^ a b エイブラハム・ウエダ 2002, p. 165.
- ^ 合原・黒崎・高橋 1999, p. 230.
- ^ 下條 1992, p. 261.
- ^ エイブラハム・ウエダ 2002, p. 192.
- ^ 船越 2008, p. 170.
- ^ a b c d e f g 合原 2011, p. 9.
- ^ a b 森・蔵本 1994, p. 151.
- ^ 下條 1992, p. 109.
- ^ a b 船越 2008, p. 11.
- ^ Grebogi/Yorke 1999, p. 2.
- ^ a b 船越 2008, p. 12.
- ^ 井上 1997, p. 26.
- ^ 下條 1992, p. 64.
- ^ Weisstein, Eric W. “Chaos”. MathWorld. Wolfram Research. 2014年12月11日閲覧。
- ^ 早間 2002, p. 57.
- ^ Devaney 1990, p. 40.
- ^ a b Devaney 1990, p. 39.
- ^ Devaney 1990, p. 13.
- ^ a b 山口昌哉・蔵本由紀. “複雑な現象に立ち向かう現代物理学 多様性に潜む「コト」の不変性 Chap.2”. Science Talk. 東芝. 2014年12月10日閲覧。
- ^ a b Maxwell, James Clerk, Larmor, Joseph, Sir. “Matter and motion pp.13-14”. California Digital Library. University of California Libraries. 2014年12月10日閲覧。
- ^ Grebogi/Yorke 1999, p. 29.
- ^ Jules Henri Poincare (1890) "Sur le probleme des trois corps et les equations de la dynamique. Divergence des series de M. Lindstedt," Acta Mathematica, vol. 13, pages 1?270.
- ^ Florin Diacu and Philip Holmes (1996) Celestial Encounters: The Origins of Chaos and Stability, Princeton University Press.
- ^ B. van der Pol and J. van der Mark (1927) "Frequency demultiplication," Nature, vol. 120, pages 363?364. See also: Van der Pol oscillator
- ^ a b 合原 1990, p. 21.
- ^ 合原 1990, p. 20.
- ^ エイブラハム・ウエダ 2002, p. 158.
- ^ Edward N. Lorenz, "Deterministic non-periodic flow," Journal of the Atmospheric Sciences, vol. 20, pages 130?141 (1963).
- ^ 合原・黒崎・高橋 1999, p. 43.
- ^ エイブラハム・ウエダ 2002, p. 53.
参考文献
- 下條隆嗣、1992、『カオス力学入門 ―古典力学からカオス力学へ』初版、 近代科学社〈シミュレーション物理学6〉 ISBN 4-7649-2005-0
- Robert L. Devaney、後藤憲一(訳)、1990、『カオス力学系入門 第2版』初版、 共立出版 ISBN 4-320-03280-2
- 合原一幸・黒崎政男・高橋純、遠藤諭(編)、1999、『哲学者クロサキと工学者アイハラの神はカオスに宿りたもう』初版、 アスキー ISBN 4-7561-3133-6
- 井上政義、1997、『やさしくわかるカオスと複雑系の科学』初版、 日本実業出版社 ISBN 4-53402492-4
- ラルフ・エイブラハムほか、ラルフ・エイブラハム、ヨシスケ・ウエダ(編)、稲垣耕作・赤松則男(訳)、2002、『カオスはこうして発見された』初版、 共立出版 ISBN 4-320-03418-X
- Celso Grebogi, James A. Yorke(編)、香田徹ほか(訳)、1999、『カオス・インパクト ―カオスは自然科学と社会科学に何をもたらしたか』第1版、 森北出版 ISBN 4-627-21321-2
- 合原一幸ほか、合原一幸(編)、1990、『カオス ―カオス理論の基礎と応用』初版、 サイエンス社 ISBN 4-7819-0592-7
- 池口徹・山田泰司・小室元政、合原一幸(編)、2011、『カオス時系列解析の基礎と応用』第4刷、 産業図書 ISBN 978-4-7828-1010-1
- 船越満明、2008、『カオス』初版、 朝倉書店〈シリーズ 非線形科学入門3〉 ISBN 978-4-254-11613-7
- K.T.アリグッド・T.D.サウアー・J.A.ヨーク、シュプリンガー・ジャパン(編)、津田一郎(監訳)、星野高志・阿部巨仁・黒田拓・松本和宏(訳)、2012、『カオス 第1巻 力学系入門』、丸善出版 ISBN 978-4-621-06223-4
- E. N Lorenz、杉山勝・杉山智子(訳)、1997、『ローレンツ カオスのエッセンス』初版、 共立出版 ISBN 4-320-00895-2
- 森肇・蔵本由紀、1994、『散逸構造とカオス』、岩波書店 ISBN 4-00-010445-4
- 早間慧、2002、『カオス力学の基礎』改訂2版、 現代数学社 ISBN 4-7687-0282-1
関連項目
- カオス
- 渾沌
- 複雑系
- 不確定性原理
- 力学系
- 分岐
- アトラクター
- フラクタル
- フラクタル次元
- ハウスドルフ次元
- リアプノフ指数
- ローレンツ方程式
- テント写像
- 構造安定
- セル・オートマトン
- カオスの縁
- 非線形科学
- ランダムウォーク
- ドゥッチ数列
- カタストロフィー理論
- 量子カオス
- ブロックエントロピー
- シャルコフスキーの定理
- カオスゲーム
- バタフライ効果
- 自己組織化
- 散逸構造
力学系は一般的にひとつあるいは複数の微分方程式あるいは差分方程式により表される。これらの方程式は短い時間区間における力学系の挙動を記述するので、より長い時間区間における力学系の挙動を決定するためには、その方程式を積分する必要がある。このためにしばしばコンピュータが効果的に用いられる。
実世界における力学系は散逸的であることが多いとされる。すなわち、もし力学系に運動の駆動力が無ければ、運動は停止するものと考えられている(そのような散逸は、様々な原因による内部摩擦や熱力学的損失、物質の損失などにより生じうる)。散逸と駆動力が組み合わさることにより、初期の摂動を鎮め、その力学系の振る舞いを典型的なものへと落ち着かせる傾向にある。そのような典型的な振る舞いに対応している力学系からなる位相空間の一部分はattracting section または attractee と呼ばれる。
アトラクターに似たような概念として、不変集合や極限集合が挙げられる。不変集合とは、ある力学系に対して、その集合自身に時間発展するような集合のことである。アトラクターは不変集合を含むことがある。極限集合とは、力学系の軌道の各点から、時間が無限大に向かうときに近づく点の集合である。アトラクターは極限集合であるが、アトラクターではない極限集合も存在する。ある種の力学系において、いくつかの点においては極限集合から外れる摂動を与えられた時にも収束するが、他のいくつかの点では「はねとばされて」二度とその極限集合の近くに戻らないことがあり得る。
減衰振子を例に考える。減衰振子は2つの不変集合(不動点)を持つ。最も低い位置にある と最も高い位置にある
である。
軌道はに収束するので、
は極限集合であるが、
は極限集合ではない。エネルギー散逸があるため、
はアトラクターでもある。振り子の振動が減衰せず、エネルギーの散逸がなければ、
はアトラクターにはならない。
数学的定義
f(t, •) を、力学系の運動状態を決定づける関数として、以下のように定義する。ある時間 t = 0 における系の状態を表す位相空間上の点を a とすると、f(0, a) = a である。また、正の値 t > 0 に対しては、f(t, a) はその状態 a が時間 t だけ経過して発展した状態を与える。例えば、一次元空間上で座標 x から速度 v で等速直線運動する粒子(t = 0 での位相空間上での座標が (x, v) )の力学系の f は
と表せる。
アトラクターは、位相空間の部分集合 A で以下の三つの条件を満たすようなものである。
- 集合 A は関数 f に対し前方不変である。すなわち、a ∈ A ならば、任意の t > 0 に対して f(t, a) ∈ A である。
- Aのある近傍で吸引流域 (basin of attraction) B(A) が存在する。B(A) は極限 t → ∞ において集合 A に含まれるすべての点 b からなる集合である。より厳密に言えば、B(A) は以下の性質を満たすようなすべての点 b からなる集合である。
- 集合 A の任意の開近傍 N に対し、ある正の定数 T > 0 が存在し、f(t, b) ∈ N が任意の実数 t > T に対して成立する。
- 集合Aの真部分集合で上の二つの性質をみたすようなものは存在しない。
吸引流域は集合 A を含むようなある開集合を含むため、A に十分近いすべての点は A に吸引されることとなる。アトラクターの定義では、考えられている位相空間上の距離を用いたが、基本的には定義の指す内容は距離関数のとり方によらず位相空間のトポロジーにのみ依存する。Rn の場合では、一般的にユークリッドノルムが用いられる。
アトラクターの定義に関しては、文献により多くの異なる定義がなされることがある。 例えば、点がアトラクターとなることを避けるためにアトラクターは正の測度を持つべきであると制限をかけたり、B(A)が近傍でなくてはならないという条件を緩めたりしている。
アトラクターの形状の種類
アトラクターは力学系の位相空間の部分集合である。1960年代頃の教科書によると、それまではアトラクターは位相空間の「幾何学的な」部分集合(点、直線、曲面、体積領域)であると考えられていた。観測されていた(位相幾何学的に)「悪い」集合(wild sets)は、取るに足らない例外であると考えられていた。スティーヴン・スメイルは彼の考案した蹄鉄型写像が構造安定であること、およびそのアトラクターがカントール集合の構造を持つことを示すことに成功した。
二つの簡単なアトラクターとしては、不動点とリミットサイクルが挙げられる。その他にも多くの幾何学的な集合がアトラクターであり得る。それらの集合(あるいは集合上での動き)を図示することが困難である場合、そのアトラクターはストレンジアトラクターと呼ばれる(後述)。
不動点

一般的に、不動点とは関数の点で変換に対して変化しないものである。
力学系の発展を一連の座標変換の過程の連続であると見做した時、その全ての過程の下で不動のものとして固定し続ける点が存在する可能性がある。一般的にはそのような点は存在しない場合が多いが、存在する場合もあり得る。
落下する小石や、減衰振子や、グラスの中の水などが最終的に落ち着くような状態である最終状態で、ある力学系がそこに向かうようなものは、その発展関数の不動点に対応し、そのような最終状態はアトラクターにおいても起こるであろうが、その二つの概念は同値であるとはいえない。あるボウルの周囲を回るビー玉は、たとえ物理学的な空間においては不動点を持たなくても、位相空間においては持つ可能性がある。そのビー玉が運動量を失い、そのボウルの底に落ち着いたなら、そのビー玉は物理空間および位相空間において一つの不動点を持ち、その力学系のアトラクターに位置することになる。
リミットサイクル
リミットサイクルは系の周期的軌道であり、孤立している。例えば振り子時計の振り子、ラジオのチューニング回路、安静時の心拍などがそれに当たる。理想的な振り子は軌道が孤立していないのでリミットサイクルではない。理想的な振り子の位相空間では、周期軌道の任意の点に対して別の周期軌道に属する点が存在する。
リミットトーラス
リミットサイクルの状態を通しての系の周期的軌道には複数の周期が存在する場合もある。それら周期のうち2つが無理数を形成するとき、その軌道はもはや閉じておらず、リミットサイクルはリミットトーラスとなる。 個の不整合周期があるとき、このようなアトラクターを
-トーラスと呼ぶ。下図は2-トーラスの例である。
 このアトラクターに対応する時系列(不整合周期を持つ
このアトラクターに対応する時系列(不整合周期を持つ周期関数の総和を離散標本化したもの。正弦波である必要はない)は「準周期的 (quasiperiodic)」である。そのような時系列は厳密には周期的ではないが、そのパワースペクトルは鋭い線からのみ成る。
ストレンジアトラクター
非整数次元のアトラクターやカオス理論でしか振る舞いを説明できない力学系のアトラクターをストレンジであると(非形式的に)いう。元はカオスアトラクターと呼ばれていたが、ダヴィッド・ルエールと Floris Takens が流体の力学系における一連の分岐の結果として生じるアトラクターを指してストレンジアトラクターという造語を使用した。ストレンジアトラクターという場合、カントール集合と非可算無限集合の直積構造を持つことが多い。
ストレンジアトラクターの例として、エノンアトラクター、レスラーアトラクター、ローレンツアトラクター、Tamariアトラクターなどがある。
参考文献
- Edward N. Lorenz (1996) The Essence of Chaos ISBN 0-295-97514-8
- James Gleick (1988) Chaos: Making a New Science ISBN 0-140-09250-1
- David Ruelle and Floris Takens (1971年). “On the nature of turbulence”. Communications of Mathematical Physics 20: 167–192. doi:10.1007/BF01646553.
- D. Ruelle (1981年). “Small random perturbations of dynamical systems and the definition of attractors”. Communications of Mathematical Physics 82: 137–151. doi:10.1007/BF01206949.
- John Milnor (1985年). “On the concept of attractor”. Communications of Mathematical Physics 99: 177–195. doi:10.1007/BF01212280.
- J. Milnor (main author) Attractor on scholarpedia.
- David Ruelle (1989年). Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press. ISBN 0-12-601710-7.
- Ruelle, David (2006年8月). “What is...a Strange Attractor?” (PDF). Notices of the American Mathematical Society 53 (7): pp.764–765 2008年1月16日閲覧。.
- Ben Tamari (1997年). Conservation and Symmetry Laws and Stabilization Programs in Economics. Ecometry ltd. ISBN 965-222-838-9.
関連項目
外部リンク
- ストレンジアトラクターの画像 その1、 その2、動画
- Chaoscope 3次元ストレンジアトラクターを描画するフリーウェア
- Attractors 1次元、2次元、3次元のストレンジアトラクターについて
- Strange Attractor Javaアプレットによる生成ソフト
- Online strange attractors generator

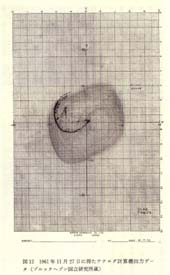




複雑系を超えて―カオス発見から未来へ 単行本 – 1999/2/1
返信削除上田 ヨシ亮 (著), 稲垣 耕作 (著), 西村 和雄 (著)
12:
返信削除非線形のデターミニスティックなシステムに生じるランダム(あるいはストカスティック、イレギュラー、アンプレディクタブル)な振動現象をカオスという
上田