http://ja.wikipedia.org/wiki/ミンコフスキー空間
http://de.wikisource.org/wiki/Raum_und_Zeit_%28Minkowski%29
Raum und Zeit
空間と時間
Hermann Minkowski, Göttingen
ハーマン・ミンコフスキー
M. H.! Die Anschauungen über Raum und Zeit, die ich Ihnen entwickeln möchte, sind auf experimentell-physikalischem Boden erwachsen. Darin liegt ihre Stärke. Ihre Tendenz ist eine radikale. Von Stund′ an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.
皆さん! 私があなたがたに説明したいと思う空間と時間についての見方
は、実験物理学の土壌に成長したもので、そこにその強さがある。それの傾
向はラディカルなものである。今からは,空間それ自体や時間それ自体は完
全に陰に沈み、両者の一種の統合だけが独立性を保つことになるだろう。
Raum und Zeit (Minkowski)
1908
邦訳
空間と時間
『相対論』東海大学出版会1969年
→自動翻訳、英語版(http://en.wikisource.org/wiki/Space_and_Time、英語版自動翻訳)
[1] M. H.! Die Anschauungen über Raum und Zeit, die ich Ihnen entwickeln möchte, sind auf experimentell-physikalischem Boden erwachsen. Darin liegt ihre Stärke. Ihre Tendenz ist eine radikale. Von Stund′ an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.
Ich möchte zunächst ausführen, wie man von der gegenwärtig angenommenen Mechanik wohl durch eine rein mathematische Überlegung zu veränderten Ideen über Raum und Zeit kommen könnte. Die Gleichungen der Newtonschen Mechanik zeigen eine zweifache Invarianz. Einmal bleibt ihre Form erhalten, wenn man das zugrunde gelegte räumliche Koordinatensystem einer beliebigen Lagenveränderung unterwirft, zweitens, wenn man es in seinem Bewegungszustande verändert, nämlich ihm irgendeine gleichförmige Translation aufprägt; auch spielt der Nullpunkt der Zeit keine Rolle. Man ist gewohnt, die Axiome der Geometrie als erledigt anzusehen, wenn man sich reif für die Axiome der Mechanik fühlt, und deshalb werden jene zwei Invarianzen wohl selten in einem Atemzuge genannt. Jede von ihnen bedeutet eine gewisse Gruppe von Transformationen in sich für die Differentialgleichungen der Mechanik. Die Existenz der ersteren Gruppe sieht man als einen fundamentalen Charakter des Raumes an. Die zweite Gruppe straft man am liebsten mit Verachtung, um leichten Sinnes darüber hinwegzukommen, daß man von den physikalischen Erscheinungen her niemals entscheiden kann, ob der als ruhend vorausgesetzte Raum sich nicht am Ende in einer gleichförmigen Translation befindet. So führen jene zwei Gruppen ein völlig getrenntes Dasein nebeneinander. Ihr gänzlich heterogener Charakter mag davon abgeschreckt haben, sie zu komponieren. Aber gerade die komponierte volle Gruppe als Ganzes gibt uns zu denken auf.
Wir wollen uns die Verhältnisse graphisch zu veranschaulichen suchen. Es seien
 rechtwinklige Koordinaten für den Raum, und
rechtwinklige Koordinaten für den Raum, und 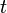 bezeichne die Zeit. Gegenstand unserer Wahrnehmung sind immer nur Orte und Zeiten verbunden. Es hat niemand einen Ort anders
bezeichne die Zeit. Gegenstand unserer Wahrnehmung sind immer nur Orte und Zeiten verbunden. Es hat niemand einen Ort anders[2] bemerkt als zu einer Zeit, eine Zeit anders als an einem Orte. Ich respektiere aber noch das Dogma, daß Raum und Zeit je eine unabhängige Bedeutung haben. Ich will einen Raumpunkt zu einem Zeitpunkt, d. i. ein Wertsystem
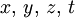 einen Weltpunkt nennen. Die Mannigfaltigkeit aller denkbaren Wertsysteme
einen Weltpunkt nennen. Die Mannigfaltigkeit aller denkbaren Wertsysteme 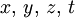 soll die Welt heißen. Ich könnte mit kühner Kreide vier Weltachsen auf die Tafel werfen. Schon eine gezeichnete Achse besteht aus lauter schwingenden Molekülen und macht zudem die Reise der Erde im All mit, gibt also bereits genug zu abstrahieren auf; die mit der Anzahl 4 verbundene etwas größere Abstraktion tut dem Mathematiker nicht wehe. Um nirgends eine gähnende Leere zu lassen, wollen wir uns vorstellen, daß aller Orten und zu jeder Zeit etwas Wahrnehmbares vorhanden ist. Um nicht Materie oder Elektrizität zu sagen, will ich für dieses Etwas das Wort Substanz brauchen. Wir richten unsere Aufmerksamkeit auf den im Weltpunkt
soll die Welt heißen. Ich könnte mit kühner Kreide vier Weltachsen auf die Tafel werfen. Schon eine gezeichnete Achse besteht aus lauter schwingenden Molekülen und macht zudem die Reise der Erde im All mit, gibt also bereits genug zu abstrahieren auf; die mit der Anzahl 4 verbundene etwas größere Abstraktion tut dem Mathematiker nicht wehe. Um nirgends eine gähnende Leere zu lassen, wollen wir uns vorstellen, daß aller Orten und zu jeder Zeit etwas Wahrnehmbares vorhanden ist. Um nicht Materie oder Elektrizität zu sagen, will ich für dieses Etwas das Wort Substanz brauchen. Wir richten unsere Aufmerksamkeit auf den im Weltpunkt 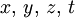 vorhandenen substantiellen Punkt und stellen uns vor, wir sind imstande, diesen substantiellen Punkt zu jeder anderen Zeit wieder zu erkennen. Einem Zeitelement
vorhandenen substantiellen Punkt und stellen uns vor, wir sind imstande, diesen substantiellen Punkt zu jeder anderen Zeit wieder zu erkennen. Einem Zeitelement  mögen die Änderungen
mögen die Änderungen  der Raumkoordinaten dieses substantiellen Punktes entsprechen. Wir erhalten alsdann als Bild sozusagen für den ewigen Lebenslauf des substantiellen Punktes eine Kurve in der Welt, eine Weltlinie, deren Punkte sich eindeutig auf den Parameter
der Raumkoordinaten dieses substantiellen Punktes entsprechen. Wir erhalten alsdann als Bild sozusagen für den ewigen Lebenslauf des substantiellen Punktes eine Kurve in der Welt, eine Weltlinie, deren Punkte sich eindeutig auf den Parameter 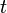 von
von 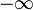 bis
bis  beziehen lassen. Die ganze Welt erscheint aufgelöst in solche Weltlinien, und ich möchte sogleich vorwegnehmen, daß meiner Meinung nach die physikalischen Gesetze ihren vollkommensten Ausdruck als Wechselbeziehungen unter diesen Weltlinien finden dürften.
beziehen lassen. Die ganze Welt erscheint aufgelöst in solche Weltlinien, und ich möchte sogleich vorwegnehmen, daß meiner Meinung nach die physikalischen Gesetze ihren vollkommensten Ausdruck als Wechselbeziehungen unter diesen Weltlinien finden dürften.Durch die Begriffe Raum und Zeit fallen die
 -Mannigfaltigkeit
-Mannigfaltigkeit 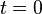 und ihre zwei Seiten
und ihre zwei Seiten 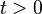 und
und  auseinander. Halten wir der Einfachheit wegen den Nullpunkt von Raum und Zeit fest, so bedeutet die zuerst genannte Gruppe der Mechanik, daß wir die
auseinander. Halten wir der Einfachheit wegen den Nullpunkt von Raum und Zeit fest, so bedeutet die zuerst genannte Gruppe der Mechanik, daß wir die  -Achsen in
-Achsen in 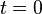 einer beliebigen Drehung um den Nullpunkt unterwerfen dürfen, entsprechend den homogenen linearen Transformationen des Ausdrucks
einer beliebigen Drehung um den Nullpunkt unterwerfen dürfen, entsprechend den homogenen linearen Transformationen des Ausdrucks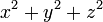 |
in sich. Die zweite Gruppe aber bedeutet, daß wir, ebenfalls ohne den Ausdruck der mechanischen Gesetze zu verändern,
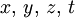 durch durch  |
mit irgendwelchen Konstanten
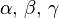 ersetzen dürfen. Der Zeitachse kann hiernach eine völlig beliebige Richtung nach der oberen halben Welt
ersetzen dürfen. Der Zeitachse kann hiernach eine völlig beliebige Richtung nach der oberen halben Welt 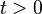 gegeben werden. Was hat nun die Forderung der Orthogonalitat
gegeben werden. Was hat nun die Forderung der Orthogonalitat[3] im Raume mit dieser völligen Freiheit der Zeitachse nach oben hin zu tun?
Die Verbindung herzustellen, nehmen wir einen positiven Parameter
 und betrachten das Gebilde
und betrachten das Gebilde |
Es besteht aus zwei durch
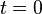 getrennten Schalen nach Analogie eines zweischaligen Hyperboloids. Wir betrachten die Schale im Gebiete
getrennten Schalen nach Analogie eines zweischaligen Hyperboloids. Wir betrachten die Schale im Gebiete  und wir fassen jetzt diejenigen homogenen linearen Transformationen von
und wir fassen jetzt diejenigen homogenen linearen Transformationen von 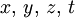 in vier neue Variable
in vier neue Variable 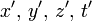 auf, wobei der Ausdruck dieser Schale in den neuen Variabeln entsprechend wird. Zu diesen Transformationen gehören offenbar die Drehungen des Raumes um den Nullpunkt. Ein volles
auf, wobei der Ausdruck dieser Schale in den neuen Variabeln entsprechend wird. Zu diesen Transformationen gehören offenbar die Drehungen des Raumes um den Nullpunkt. Ein vollesVerständnis der übrigen jener Transformationen erhalten wir hernach bereits, wenn wir eine solche unter ihnen ins Auge fassen, bei der
 und
und  ungeändert bleiben. Wir zeichnen (Fig. 1) den Durchschnitt jener Schale mit der Ebene der
ungeändert bleiben. Wir zeichnen (Fig. 1) den Durchschnitt jener Schale mit der Ebene der  - und der
- und der 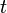 -Achse, den oberen Ast der Hyperbel
-Achse, den oberen Ast der Hyperbel  mit seinen Asymptoten. Ferner werde ein beliebiger Radiusvektor
mit seinen Asymptoten. Ferner werde ein beliebiger Radiusvektor 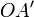 dieses Hyperbelastes vom Nullpunkte
dieses Hyperbelastes vom Nullpunkte  aus eingetragen, die Tangente in
aus eingetragen, die Tangente in  an die Hyperbel bis zum Schnitte
an die Hyperbel bis zum Schnitte  mit der Asymptote rechts gelegt,
mit der Asymptote rechts gelegt, 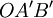 zum Parallelogramm
zum Parallelogramm  vervollständigt, endlich für das spätere noch
vervollständigt, endlich für das spätere noch  bis zum Schnitt
bis zum Schnitt  mit der
mit der  -Achse durchgeführt. Nehmen wir nun
-Achse durchgeführt. Nehmen wir nun  und
und 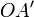 als Achsen für Parallelkoordinaten
als Achsen für Parallelkoordinaten 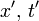 mit den Maßstäben
mit den Maßstäben  so erlangt jener Hyperbelast wieder den Ausdruck
so erlangt jener Hyperbelast wieder den Ausdruck  und der Übergang von
und der Übergang von 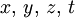 zu
zu 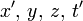 ist eine der fraglichen Transformationen. Wir nehmen nun zu den charakterisierten Transformationen noch die beliebigen Verschiebungen des Raum- und Zeit-Nullpunktes hinzu und konstituieren damit eine offenbar noch von dem Parameter
ist eine der fraglichen Transformationen. Wir nehmen nun zu den charakterisierten Transformationen noch die beliebigen Verschiebungen des Raum- und Zeit-Nullpunktes hinzu und konstituieren damit eine offenbar noch von dem Parameter  abhängige Gruppe von Transformationen, die ich mit
abhängige Gruppe von Transformationen, die ich mit  bezeichne.
bezeichne.Lassen wir jetzt
 ins Unendliche wachsen, also
ins Unendliche wachsen, also 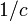 nach Null konvergieren, so leuchtet an der beschriebenen Figur ein, daß der Hyperbelast sich immer mehr der
nach Null konvergieren, so leuchtet an der beschriebenen Figur ein, daß der Hyperbelast sich immer mehr der  -Achse anschmiegt, der Asymptotenwinkel sich zu einem gestreckten verbreitert, jene spezielle Transformation in der Grenze sich in eine solche verwandelt, wobei die
-Achse anschmiegt, der Asymptotenwinkel sich zu einem gestreckten verbreitert, jene spezielle Transformation in der Grenze sich in eine solche verwandelt, wobei die 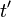 -Achse eine beliebige Richtung nach oben haben kann und
-Achse eine beliebige Richtung nach oben haben kann und 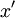 immer genauer sich an
immer genauer sich an  annähert. Mit Rücksicht hierauf ist klar, daß aus der
annähert. Mit Rücksicht hierauf ist klar, daß aus der[4] Gruppe
 in der Grenze für
in der Grenze für  also als Gruppe
also als Gruppe  eben jene zu der Newtonschen Mechanik gehörige volle Gruppe wird. Bei dieser Sachlage, und da
eben jene zu der Newtonschen Mechanik gehörige volle Gruppe wird. Bei dieser Sachlage, und da  mathematisch verständlicher ist als
mathematisch verständlicher ist als  hätte wohl ein Mathematiker in freier Phantasie auf den Gedanken verfallen können, daß am Ende die Naturerscheinungen tatsächlich eine Invarianz nicht bei der Gruppe
hätte wohl ein Mathematiker in freier Phantasie auf den Gedanken verfallen können, daß am Ende die Naturerscheinungen tatsächlich eine Invarianz nicht bei der Gruppe  sondern vielmehr bei einer Gruppe
sondern vielmehr bei einer Gruppe  mit bestimmtem endlichen, nur in den gewöhnlichen Maßeinheiten äußerst großen
mit bestimmtem endlichen, nur in den gewöhnlichen Maßeinheiten äußerst großen  besitzen. Eine solche Ahnung wäre ein außerordentlicher Triumph der reinen Mathematik gewesen. Nun, da die Mathematik hier nur mehr Treppenwitz bekundet, bleibt ihr doch die Genugtuung, daß sie dank ihren glücklichen Antezedenzien mit ihren in freier Fernsicht geschärften Sinnen die tiefgreifenden Konsequenzen einer solcher Ummodelung unserer Naturauffassung auf der Stelle zu erfassen vermag.
besitzen. Eine solche Ahnung wäre ein außerordentlicher Triumph der reinen Mathematik gewesen. Nun, da die Mathematik hier nur mehr Treppenwitz bekundet, bleibt ihr doch die Genugtuung, daß sie dank ihren glücklichen Antezedenzien mit ihren in freier Fernsicht geschärften Sinnen die tiefgreifenden Konsequenzen einer solcher Ummodelung unserer Naturauffassung auf der Stelle zu erfassen vermag.Ich will sogleich bemerken, um welchen Wert für
 es sich schließlich handeln wird. Für
es sich schließlich handeln wird. Für  wird die Fortpflanzungsgeschwindigkeit des Lichtes im leeren Raume eintreten. Um weder vom Raum noch von Leere zu sprechen, können wir diese Größe wieder als das Verhältnis der elektrostatischen und der elektromagnetischen Einheit der Elektrizitätsmenge kennzeichnen.
wird die Fortpflanzungsgeschwindigkeit des Lichtes im leeren Raume eintreten. Um weder vom Raum noch von Leere zu sprechen, können wir diese Größe wieder als das Verhältnis der elektrostatischen und der elektromagnetischen Einheit der Elektrizitätsmenge kennzeichnen.Das Bestehen der Invarianz der Naturgesetze für die bezügliche Gruppe
 würde nun so zu fassen sein:
würde nun so zu fassen sein:Man kann aus der Gesamtheit der Naturerscheinungen durch sukzessiv gesteigerte Approximationen immer genauer ein Bezugsystem
 und
und  Raum und Zeit, ableiten, mittels dessen diese Erscheinungen sich dann nach bestimmten Gesetzen darstellen. Dieses Bezugsystem ist dabei aber durch die Erscheinungen keineswegs eindeutig festgelegt. Man kann das Bezugsystem noch entsprechend den Transformationen der genannten Gruppe
Raum und Zeit, ableiten, mittels dessen diese Erscheinungen sich dann nach bestimmten Gesetzen darstellen. Dieses Bezugsystem ist dabei aber durch die Erscheinungen keineswegs eindeutig festgelegt. Man kann das Bezugsystem noch entsprechend den Transformationen der genannten Gruppe  beliebig verändern, ohne daß der Ausdruck der Naturgesetze sich dabei verändert.
beliebig verändern, ohne daß der Ausdruck der Naturgesetze sich dabei verändert.Z. B. kann man der beschriebenen Figur entsprechend auch
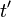 Zeit benennen, muß dann aber im Zusammenhange damit notwendig den Raum durch die Mannigfaltigkeit der drei Parameter
Zeit benennen, muß dann aber im Zusammenhange damit notwendig den Raum durch die Mannigfaltigkeit der drei Parameter  definieren, wobei nun die physikalischen Gesetze mittels
definieren, wobei nun die physikalischen Gesetze mittels 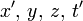 sich genau ebenso ausdrücken würden, wie mittels
sich genau ebenso ausdrücken würden, wie mittels  Hiernach würden wir dann in der Welt nicht mehr den Raum, sondern unendlich viele Räume haben, analog wie es im dreidimensionalen Räume unendlich viele Ebenen gibt. Die dreidimensionale Geometrie wird ein Kapitel der vierdimensionalen Physik. Sie erkennen, weshalb ich am Eingange sagte, Raum und Zeit sollen zu Schatten herabsinken und nur eine Welt an sich bestehen.
Hiernach würden wir dann in der Welt nicht mehr den Raum, sondern unendlich viele Räume haben, analog wie es im dreidimensionalen Räume unendlich viele Ebenen gibt. Die dreidimensionale Geometrie wird ein Kapitel der vierdimensionalen Physik. Sie erkennen, weshalb ich am Eingange sagte, Raum und Zeit sollen zu Schatten herabsinken und nur eine Welt an sich bestehen.[5]
Nun ist die Frage, welche Umstände zwingen uns die veränderte Auffassung von Raum und Zeit auf, widerspricht sie tatsächlich niemals den Erscheinungen, endlich gewährt sie Vorteile für die Beschreibung der Erscheinungen?
Bevor wir hierauf eingehen, sei eine wichtige Bemerkung vorangestellt. Haben wir Raum und Zeit irgendwie individualisiert, so entspricht einem ruhenden substantiellen Punkte als Weltlinie eine zur
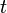 -Achse parallele Gerade, einem gleichförmig bewegten substantiellen Punkte eine gegen die
-Achse parallele Gerade, einem gleichförmig bewegten substantiellen Punkte eine gegen die 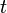 -Achse geneigte Gerade, einem ungleichförmig bewegten substantiellen Punkte eine irgendwie gekrümmte Weltlinie. Fassen wir in einem beliebigen Weltpunkte
-Achse geneigte Gerade, einem ungleichförmig bewegten substantiellen Punkte eine irgendwie gekrümmte Weltlinie. Fassen wir in einem beliebigen Weltpunkte 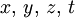 die dort durchlaufende Weltlinie auf, und finden wir sie dort parallel mit irgendeinem Radiusvektor
die dort durchlaufende Weltlinie auf, und finden wir sie dort parallel mit irgendeinem Radiusvektor 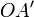 der vorhin genannten hyperboloidischen Schale, so können wir
der vorhin genannten hyperboloidischen Schale, so können wir 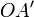 als neue Zeitachse einführen, und bei den damit gegebenen neuen Begriffen von Raum und Zeit erscheint die Substanz in dem betreffenden Weltpunkte als ruhend. Wir wollen nun dieses fundamentale Axiom einführen:
als neue Zeitachse einführen, und bei den damit gegebenen neuen Begriffen von Raum und Zeit erscheint die Substanz in dem betreffenden Weltpunkte als ruhend. Wir wollen nun dieses fundamentale Axiom einführen:Die in einem beliebigen Weltpunkte vorhandene Substanz kann stets bei geeigneter Festsetzung von Raum und Zeit als ruhend aufgefaßt werden.
Das Axiom bedeutet, daß in jedem Weltpunkte stets der Ausdruck
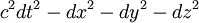 |
positiv ausfällt oder, was damit gleichbedeutend ist, daß jede Geschwindigkeit
 stets kleiner als
stets kleiner als  ausfällt. Es würde danach für alle substantiellen Geschwindigkeiten
ausfällt. Es würde danach für alle substantiellen Geschwindigkeiten  als obere Grenze bestehen und hierin eben die tiefere Bedeutung der Größe
als obere Grenze bestehen und hierin eben die tiefere Bedeutung der Größe  liegen. In dieser anderen Fassung hat das Axiom beim ersten Eindruck etwas Mißfälliges. Es ist aber zu bedenken, daß nun eine modifizierte Mechanik Platz greifen wird, in der die Quadratwurzel aus jener Differentialverbindung zweiten Grades eingeht, so daß Fälle mit Überlichtgeschwindigkeit nur mehr eine Rolle spielen werden, etwa wie in der Geometrie Figuren mit imaginären Koordinaten.
liegen. In dieser anderen Fassung hat das Axiom beim ersten Eindruck etwas Mißfälliges. Es ist aber zu bedenken, daß nun eine modifizierte Mechanik Platz greifen wird, in der die Quadratwurzel aus jener Differentialverbindung zweiten Grades eingeht, so daß Fälle mit Überlichtgeschwindigkeit nur mehr eine Rolle spielen werden, etwa wie in der Geometrie Figuren mit imaginären Koordinaten.Der Anstoß und wahre Beweggrund für die Annahme der Gruppe
 nun kam daher, daß die Differentialgleichung für die Fortpflanzung von Lichtwellen im leeren Raume jene Gruppe
nun kam daher, daß die Differentialgleichung für die Fortpflanzung von Lichtwellen im leeren Raume jene Gruppe  besitzt.[1] Andererseits hat der Begriff starrer Körper nur in einer Mechanik mit der Gruppe
besitzt.[1] Andererseits hat der Begriff starrer Körper nur in einer Mechanik mit der Gruppe  einen Sinn. Hat man nun eine Optik mit
einen Sinn. Hat man nun eine Optik mit 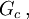 und gäbe es andererseits
und gäbe es andererseits[6] starre Körper, so ist leicht abzusehen, daß durch die zwei zu
 und zu
und zu 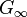 gehörigen hyperboloidischen Schalen eine
gehörigen hyperboloidischen Schalen eine 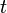 -Richtung ausgezeichnet sein würde, und das würde weiter die Konsequenz haben, daß man an geeigneten starren optischen Instrumenten im Laboratorium einen Wechsel der Erscheinungen bei verschiedener Orientierung gegen die Fortschreitungsrichtung der Erde müßte wahrnehmen können. Alle auf dieses Ziel gerichteten Bemühungen, insbesondere ein berühmter Interferenzversuch von Michelson, hatten jedoch ein negatives Ergebnis. Um eine Erklärung hierfür zu gewinnen, bildete H. A. Lorentz eine Hypothese, deren Erfolg eben in der Invarianz der Optik für die Gruppe
-Richtung ausgezeichnet sein würde, und das würde weiter die Konsequenz haben, daß man an geeigneten starren optischen Instrumenten im Laboratorium einen Wechsel der Erscheinungen bei verschiedener Orientierung gegen die Fortschreitungsrichtung der Erde müßte wahrnehmen können. Alle auf dieses Ziel gerichteten Bemühungen, insbesondere ein berühmter Interferenzversuch von Michelson, hatten jedoch ein negatives Ergebnis. Um eine Erklärung hierfür zu gewinnen, bildete H. A. Lorentz eine Hypothese, deren Erfolg eben in der Invarianz der Optik für die Gruppe  liegt. Nach Lorentz soll jeder Körper, der eine Bewegung besitzt, in Richtung der Bewegung eine Verkürzung erfahren haben, und zwar bei einer Geschwindigkeit
liegt. Nach Lorentz soll jeder Körper, der eine Bewegung besitzt, in Richtung der Bewegung eine Verkürzung erfahren haben, und zwar bei einer Geschwindigkeit  im Verhältnisse
im Verhältnisse |
Diese Hypothese klingt äußerst phantastisch. Denn die Kontraktion ist nicht etwa als Folge von Widerständen im Äther zu denken, sondern rein als Geschenk von oben, als Begleitumstand des Umstandes der Bewegung.
Ich will nun an unserer Figur zeigen, daß die Lorentzsche Hypothese völlig äquivalent ist mit der neuen Auffassung von Raum und Zeit, wodurch sie viel verständlicher wird. Abstrahieren wir der Einfachheit wegen von
 und
und  und denken uns eine räumlich eindimensionale Welt, so sind ein wie die
und denken uns eine räumlich eindimensionale Welt, so sind ein wie die 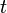 -Achse aufrechter und ein gegen die
-Achse aufrechter und ein gegen die 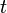 -Achse geneigter Parallelstreifen (siehe Fig. 1) Bilder für den Verlauf eines ruhenden, bezüglich eines gleichförmig bewegten Körpers, der jedesmal eine konstante räumliche Ausdehnung behält. Ist
-Achse geneigter Parallelstreifen (siehe Fig. 1) Bilder für den Verlauf eines ruhenden, bezüglich eines gleichförmig bewegten Körpers, der jedesmal eine konstante räumliche Ausdehnung behält. Ist 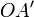 parallel dem zweiten Streifen, so können wir
parallel dem zweiten Streifen, so können wir 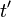 als Zeit und
als Zeit und 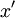 als Raumkoordinate einführen, und es erscheint dann der zweite Körper als ruhend, der erste als gleichförmig bewegt. Wir nehmen nun an, daß der erste Körper als ruhend aufgefaßt die Länge
als Raumkoordinate einführen, und es erscheint dann der zweite Körper als ruhend, der erste als gleichförmig bewegt. Wir nehmen nun an, daß der erste Körper als ruhend aufgefaßt die Länge  hat, d. h. der Querschnitt
hat, d. h. der Querschnitt 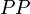 des ersten Streifens auf der
des ersten Streifens auf der  ist, wo
ist, wo  den Einheitsmaßstab auf der
den Einheitsmaßstab auf der  -Achse bedeutet, und daß andererseits der zweite Körper als ruhend aufgefaßt die gleiche Länge
-Achse bedeutet, und daß andererseits der zweite Körper als ruhend aufgefaßt die gleiche Länge  hat; letzteres heißt dann, daß der parallel der
hat; letzteres heißt dann, daß der parallel der 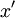 -Achse gemessene Querschnitt des zweiten Streifens,
-Achse gemessene Querschnitt des zweiten Streifens, 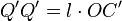 ist. Wir haben nunmehr in diesen zwei Körpern Bilder von zwei gleichen Lorentzschen Elektronen, einem ruhenden und einem gleichförmig bewegten. Halten wir aber an den ursprünglichen Koordinaten
ist. Wir haben nunmehr in diesen zwei Körpern Bilder von zwei gleichen Lorentzschen Elektronen, einem ruhenden und einem gleichförmig bewegten. Halten wir aber an den ursprünglichen Koordinaten  fest, so ist als Ausdehnung des zweiten Elektrons der Querschnitt
fest, so ist als Ausdehnung des zweiten Elektrons der Querschnitt 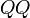 seines zugehörigen Streifens parallel der
seines zugehörigen Streifens parallel der  -Achse anzugeben. Nun ist offenbar, da
-Achse anzugeben. Nun ist offenbar, da 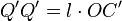
[7] ist,
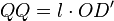 . Eine leichte Rechnung ergibt, wenn
. Eine leichte Rechnung ergibt, wenn  für den zweiten Streifen
für den zweiten Streifen 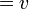 ist,
ist,  , also auch
, also auch  . Dies ist aber der Sinn der Lorentzschen Hypothese von der Kontraktion der Elektronen bei Bewegung. Fassen wir andererseits das zweite Elektron als ruhend auf, adoptieren also das Bezugsystem
. Dies ist aber der Sinn der Lorentzschen Hypothese von der Kontraktion der Elektronen bei Bewegung. Fassen wir andererseits das zweite Elektron als ruhend auf, adoptieren also das Bezugsystem  so ist als Länge des ersten der Querschnitt
so ist als Länge des ersten der Querschnitt  seines Streifens parallel
seines Streifens parallel  zu bezeichnen, und wir würden in genau dem nämlichen Verhältnisse das erste Elektron gegen das zweite verkürzt finden; denn es ist in der Figur
zu bezeichnen, und wir würden in genau dem nämlichen Verhältnisse das erste Elektron gegen das zweite verkürzt finden; denn es ist in der Figur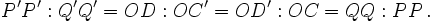 |
Lorentz nannte die Verbindung
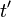 von
von  und
und 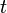 Ortszeit des gleichförmig bewegten Elektrons und verwandte eine physikalische Konstruktion dieses Begriffs zum besseren Verständnis der Kontraktionshypothese. Jedoch scharf erkannt zu haben, daß die Zeit des einen Elektrons ebenso gut wie die des anderen ist, d. h. daß
Ortszeit des gleichförmig bewegten Elektrons und verwandte eine physikalische Konstruktion dieses Begriffs zum besseren Verständnis der Kontraktionshypothese. Jedoch scharf erkannt zu haben, daß die Zeit des einen Elektrons ebenso gut wie die des anderen ist, d. h. daß 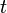 und
und 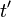 gleich zu behandeln sind, ist erst das Verdienst von A. Einstein.[2] Damit war nun zunächst die Zeit als ein durch die Erscheinungen eindeutig festgelegter Begriff abgesetzt. An dem Begriffe des Raumes rüttelten weder Einstein noch Lorentz, vielleicht deshalb nicht, weil bei der genannten speziellen Transformation, wo die
gleich zu behandeln sind, ist erst das Verdienst von A. Einstein.[2] Damit war nun zunächst die Zeit als ein durch die Erscheinungen eindeutig festgelegter Begriff abgesetzt. An dem Begriffe des Raumes rüttelten weder Einstein noch Lorentz, vielleicht deshalb nicht, weil bei der genannten speziellen Transformation, wo die 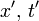 -Ebene sich mit der
-Ebene sich mit der  -Ebene deckt, eine Deutung möglich ist, als sei die
-Ebene deckt, eine Deutung möglich ist, als sei die  -Achse des Raumes in ihrer Lage erhalten geblieben. Über den Begriff des Raumes in entsprechender Weise hinwegzuschreiten, ist auch wohl nur als Verwegenheit mathematischer Kultur einzutaxieren. Nach diesem zum wahren Verständnis der Gruppe
-Achse des Raumes in ihrer Lage erhalten geblieben. Über den Begriff des Raumes in entsprechender Weise hinwegzuschreiten, ist auch wohl nur als Verwegenheit mathematischer Kultur einzutaxieren. Nach diesem zum wahren Verständnis der Gruppe  jedoch unerläßlichen weiteren Schritt aber scheint mir das Wort Relativitätspostulat für die Forderung einer Invarianz bei der Gruppe
jedoch unerläßlichen weiteren Schritt aber scheint mir das Wort Relativitätspostulat für die Forderung einer Invarianz bei der Gruppe  sehr matt. Indem der Sinn des Postulats wird, daß durch die Erscheinungen nur die in Raum und Zeit vierdimensionale Welt gegeben ist, aber die Projektion in Raum und in Zeit noch mit einer gewissen Freiheit vorgenommen werden kann, möchte ich dieser Behauptung eher den Namen Postulat der absoluten Welt (oder kurz Weltpostulat) geben.
sehr matt. Indem der Sinn des Postulats wird, daß durch die Erscheinungen nur die in Raum und Zeit vierdimensionale Welt gegeben ist, aber die Projektion in Raum und in Zeit noch mit einer gewissen Freiheit vorgenommen werden kann, möchte ich dieser Behauptung eher den Namen Postulat der absoluten Welt (oder kurz Weltpostulat) geben.Durch das Weltpostulat wird eine gleichartige Behandlung der vier Bestimmungsstücke
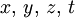 möglich. Dadurch gewinnen, wie ich jetzt
möglich. Dadurch gewinnen, wie ich jetzt[8] ausführen will, die Formen, unter denen die physikalischen Gesetze sich abspielen, an Verständlichkeit. Vor allem erlangt der Begriff der Beschleunigung ein scharf hervortretendes Gepräge.
Ich werde mich einer geometrischen Ausdrucksweise bedienen, die sich sofort darbietet, indem man im Tripel
 stillschweigend von
stillschweigend von  abstrahiert. Einen beliebigen Weltpunkt
abstrahiert. Einen beliebigen Weltpunkt  denke ich zum Raum-Zeit-Nullpunkt gemacht. Der Kegel
denke ich zum Raum-Zeit-Nullpunkt gemacht. Der Kegel |
mit
 als Spitze (Fig. 2) besteht aus zwei Teilen, einem mit Werten
als Spitze (Fig. 2) besteht aus zwei Teilen, einem mit Werten  , einem anderen mit Werten
, einem anderen mit Werten 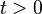 . Der erste, der Vorkegel von
. Der erste, der Vorkegel von  besteht, sagen wir, aus allen Weltpunkten, die „Licht nach
besteht, sagen wir, aus allen Weltpunkten, die „Licht nach  senden“, der zweite, der Nachkegel von
senden“, der zweite, der Nachkegel von  , aus allen Weltpunkten, die „Licht von
, aus allen Weltpunkten, die „Licht von  empfangen“. Das vom Vorkegel allein begrenzte Gebiet mag diesseits von
empfangen“. Das vom Vorkegel allein begrenzte Gebiet mag diesseits von  das vom Nachkegel allein begrenzte jenseits von
das vom Nachkegel allein begrenzte jenseits von  heißen. Jenseits
heißen. Jenseits  fällt die schon betrachtete hyperboloidische Schale
fällt die schon betrachtete hyperboloidische Schale |
Das Gebiet zwischen den Kegeln wird erfüllt von den einschaligen hyperboloidischen Gebilden
 |
zu allen konstanten positiven Werten
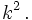 Wichtig sind für uns die Hyperbeln mit
Wichtig sind für uns die Hyperbeln mit  als Mittelpunkt, die auf den letzteren Gebilden liegen. Die einzelnen Äste dieser Hyperbeln mögen kurz die Zwischenhyperbeln zum Zentrum
als Mittelpunkt, die auf den letzteren Gebilden liegen. Die einzelnen Äste dieser Hyperbeln mögen kurz die Zwischenhyperbeln zum Zentrum  heißen. Ein solcher Hyperbelast würde, als Weltlinie eines substantiellen Punktes gedacht, eine Bewegung repräsentieren, die für
heißen. Ein solcher Hyperbelast würde, als Weltlinie eines substantiellen Punktes gedacht, eine Bewegung repräsentieren, die für  und
und 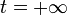 asymptotisch auf die Lichtgeschwindigkeit
asymptotisch auf die Lichtgeschwindigkeit  ansteigt.
ansteigt.Nennen wir in Analogie zum Vektorbegriff im Raume jetzt eine gerichtete Strecke in der Mannigfaltigkeit der
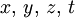 einen Vektor, so haben wir zu unterscheiden zwischen den zeitartigen Vektoren mit Richtungen von
einen Vektor, so haben wir zu unterscheiden zwischen den zeitartigen Vektoren mit Richtungen von  nach der Schale
nach der Schale  und den raumartigen Vektoren mit Richtungen von
und den raumartigen Vektoren mit Richtungen von  nach
nach  . Die Zeitachse kann jedem Vektor der ersten Art parallel laufen. Ein jeder Weltpunkt zwischen Vorkegel und Nachkegel von
. Die Zeitachse kann jedem Vektor der ersten Art parallel laufen. Ein jeder Weltpunkt zwischen Vorkegel und Nachkegel von  kann durch das Bezugsystem als gleichzeitig mit
kann durch das Bezugsystem als gleichzeitig mit  aber ebensogut auch als früher als
aber ebensogut auch als früher als  oder als später als
oder als später als  eingerichtet werden. Jeder Weltpunkt diesseits
eingerichtet werden. Jeder Weltpunkt diesseits  ist notwendig
ist notwendig[9] stets früher, jeder Weltpunkt jenseits
 notwendig stets später als
notwendig stets später als 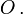 Dem Grenzübergang zu
Dem Grenzübergang zu  würde ein völliges Zusammenklappen des keilförmigen Einschnittes zwischen den Kegeln in die ebene Mannigfaltigkeit
würde ein völliges Zusammenklappen des keilförmigen Einschnittes zwischen den Kegeln in die ebene Mannigfaltigkeit 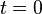 entsprechen. In den gezeichneten Figuren ist dieser Einschnitt absichtlich mit verschiedener Breite angelegt.
entsprechen. In den gezeichneten Figuren ist dieser Einschnitt absichtlich mit verschiedener Breite angelegt.Einen beliebigen Vektor wie von
 nach
nach 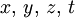 zerlegen wir in die vier Komponenten
zerlegen wir in die vier Komponenten  Sind die Richtungen zweier Vektoren beziehungsweise die eines Radiusvektors
Sind die Richtungen zweier Vektoren beziehungsweise die eines Radiusvektors  von
von  an eine der Flächen
an eine der Flächen 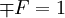 und dazu einer Tangente
und dazu einer Tangente 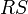 im Punkte
im Punkte  der betreffenden Fläche, so sollen die Vektoren normal zueinander heißen. Danach ist
der betreffenden Fläche, so sollen die Vektoren normal zueinander heißen. Danach ist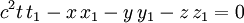 |
die Bedingung dafür, daß die Vektoren mit den Komponenten
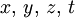 und
und  normal zueinander sind.
normal zueinander sind.Für die Beträge von Vektoren der verschiedenen Richtungen sollen die Einheitsmaßstäbe dadurch fixiert sein, daß einem raumartigen Vektor von
 nach
nach  stets der Betrag 1, einem zeitartigen Vektor von
stets der Betrag 1, einem zeitartigen Vektor von  nach
nach  stets der Betrag
stets der Betrag 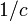 zugeschrieben wird.
zugeschrieben wird.Denken wir uns nun in einem Weltpunkte
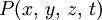 die dort durchlaufende Weltlinie eines substantiellen Punktes, so entspricht danach dem zeitartigen Vektorelement
die dort durchlaufende Weltlinie eines substantiellen Punktes, so entspricht danach dem zeitartigen Vektorelement  im Fortgang der Linie der Betrag
im Fortgang der Linie der Betrag |
Das Integral
 dieses Betrages auf der Weltlinie von irgendeinem fixierten Ausgangspunkte
dieses Betrages auf der Weltlinie von irgendeinem fixierten Ausgangspunkte 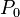 bis zu dem variablen Endpunkte
bis zu dem variablen Endpunkte  geführt, nennen wir die Eigenzeit des substantiellen Punktes in
geführt, nennen wir die Eigenzeit des substantiellen Punktes in  Auf der Weltlinie betrachten wir
Auf der Weltlinie betrachten wir  d. s. die Komponenten des Vektors
d. s. die Komponenten des Vektors 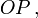 als Funktionen der Eigenzeit
als Funktionen der Eigenzeit  bezeichnen deren erste Differentialquotienten nach
bezeichnen deren erste Differentialquotienten nach  mit
mit  deren zweite Differentialquotienten nach
deren zweite Differentialquotienten nach  mit
mit  und nennen die zugehörigen Vektoren, die Ableitung des Vektors
und nennen die zugehörigen Vektoren, die Ableitung des Vektors  nach
nach  den Bewegungsvektor in
den Bewegungsvektor in 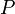 und die Ableitung dieses Bewegungsvektors nach
und die Ableitung dieses Bewegungsvektors nach  den Beschleunigungsvektor in
den Beschleunigungsvektor in 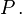 Dabei gilt
Dabei gilt |
 |
d. h. der Bewegungsvektor ist der zeitartige Vektor in Richtung der Weltlinie in
 vom Betrage 1, und der Beschleunigungsvektor in
vom Betrage 1, und der Beschleunigungsvektor in  ist normal zum Bewegungsvektor in
ist normal zum Bewegungsvektor in  also jedenfalls ein raumartiger Vektor.
also jedenfalls ein raumartiger Vektor.[10] Nun gibt es, wie man leicht einsieht, einen bestimmten Hyperbelast, der mit der Weltlinie in
 drei unendlich benachbarte Punkte gemein hat, und dessen Asymptoten Erzeugende eines Vorkegels und eines Nachkegels sind (siehe unten Fig. 3). Dieser Hyperbelast heiße die Krümmungshyperbel in
drei unendlich benachbarte Punkte gemein hat, und dessen Asymptoten Erzeugende eines Vorkegels und eines Nachkegels sind (siehe unten Fig. 3). Dieser Hyperbelast heiße die Krümmungshyperbel in  Ist
Ist 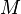 das Zentrum dieser Hyperbel, so handelt es sich also hier um eine Zwischenhyperbel zum Zentrum
das Zentrum dieser Hyperbel, so handelt es sich also hier um eine Zwischenhyperbel zum Zentrum 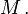 Es sei
Es sei  der Betrag des Vektors
der Betrag des Vektors 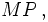 so erkennen wir den Beschleunigungsvektor in
so erkennen wir den Beschleunigungsvektor in 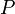 als den Vektor in Richtung
als den Vektor in Richtung  vom Betrage
vom Betrage 
Sind
 sämtlich Null, so reduziert sich die Krümmungshyperbel auf die in
sämtlich Null, so reduziert sich die Krümmungshyperbel auf die in 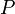 die Weltlinie berührende Gerade, und es ist
die Weltlinie berührende Gerade, und es ist  zu setzen.
zu setzen.Um darzutun, daß die Annahme der Gruppe
 für die physikalischen Gesetze nirgends zu einem Widerspruche führt, ist es unumgänglich, eine Revision der gesamten Physik auf Grund der Voraussetzung dieser Gruppe vorzunehmen. Diese Revision ist bereits in einem gewissen Umfange erfolgreich geleistet für Fragen der Thermodynamik und Wärmestrahlung[3], für die elektromagnetischen Vorgänge, endlich für die Mechanik unter Aufrechterhaltung des Massenbegriffs.[4]
für die physikalischen Gesetze nirgends zu einem Widerspruche führt, ist es unumgänglich, eine Revision der gesamten Physik auf Grund der Voraussetzung dieser Gruppe vorzunehmen. Diese Revision ist bereits in einem gewissen Umfange erfolgreich geleistet für Fragen der Thermodynamik und Wärmestrahlung[3], für die elektromagnetischen Vorgänge, endlich für die Mechanik unter Aufrechterhaltung des Massenbegriffs.[4]Für letzteres Gebiet ist vor allem die Frage aufzuwerfen: Wenn eine Kraft mit den Komponenten
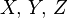 nach den Raumachsen in einem Weltpunkte
nach den Raumachsen in einem Weltpunkte 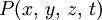 angreift, wo der Bewegungsvektor
angreift, wo der Bewegungsvektor  ist, als welche Kraft ist diese Kraft bei einer beliebigen Änderung des Bezugsystemes aufzufassen? Nun existieren gewisse erprobte Ansätze über die ponderomotorische Kraft im elektromagnetischen Felde in den Fällen, wo die Gruppe
ist, als welche Kraft ist diese Kraft bei einer beliebigen Änderung des Bezugsystemes aufzufassen? Nun existieren gewisse erprobte Ansätze über die ponderomotorische Kraft im elektromagnetischen Felde in den Fällen, wo die Gruppe  unzweifelhaft zuzulassen ist. Diese Ansätze führen zu der einfachen Regel: Bei Änderung des Bezugsystemes ist die vorausgesetzte Kraft derart als Kraft in den neuen Raumkoordinaten anzusetzen, daß dabei der zugehörige Vektor mit den Komponenten
unzweifelhaft zuzulassen ist. Diese Ansätze führen zu der einfachen Regel: Bei Änderung des Bezugsystemes ist die vorausgesetzte Kraft derart als Kraft in den neuen Raumkoordinaten anzusetzen, daß dabei der zugehörige Vektor mit den Komponenten |
wo
 |
die durch
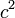 dividierte Arbeitsleistung der Kraft im Weltpunkte ist, sich unverändert erhält. Dieser Vektor ist stets normal zum Bewegungsvektor in
dividierte Arbeitsleistung der Kraft im Weltpunkte ist, sich unverändert erhält. Dieser Vektor ist stets normal zum Bewegungsvektor in 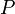 . Ein solcher, zu einer Kraft in
. Ein solcher, zu einer Kraft in 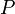 gehörender Kraftvektor soll ein bewegender Kraftvektor in
gehörender Kraftvektor soll ein bewegender Kraftvektor in 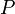 heißen.
heißen.[11] Nun werde die durch
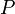 laufende Weltlinie von einem substantiellen Punkte mit konstanter mechanischer Masse
laufende Weltlinie von einem substantiellen Punkte mit konstanter mechanischer Masse  beschrieben. Das
beschrieben. Das  -fache des Bewegungsvektors in
-fache des Bewegungsvektors in 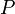 heiße der Impulsvektor in
heiße der Impulsvektor in  das
das  -fache des Beschleunigungsvektors in
-fache des Beschleunigungsvektors in 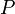 der Kraftvektor der Bewegung in
der Kraftvektor der Bewegung in 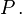 Nach diesen Definitionen lautet das Gesetz dafür, wie die Bewegung eines Massenpunktes bei gegebenem bewegenden Kraftvektor statthat:[5]
Nach diesen Definitionen lautet das Gesetz dafür, wie die Bewegung eines Massenpunktes bei gegebenem bewegenden Kraftvektor statthat:[5]Der Kraftvektor der Bewegung ist gleich dem bewegenden Kraftvektor.
Diese Aussage faßt vier Gleichungen für die Komponenten nach den vier Achsen zusammen, wobei die vierte, weil von vornherein beide genannten Vektoren normal zum Bewegungsvektor sind, sich als eine Folge der drei ersten ansehen läßt. Nach der obigen Bedeutung von
 stellt die vierte zweifellos den Energiesatz dar. Als kinetische Energie des Massenpunktes ist daher das
stellt die vierte zweifellos den Energiesatz dar. Als kinetische Energie des Massenpunktes ist daher das 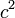 -fache der Komponente des Impulsvektors nach der
-fache der Komponente des Impulsvektors nach der 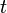 -Achse zu definieren. Der Ausdruck hierfür ist
-Achse zu definieren. Der Ausdruck hierfür ist |
d. i. nach Abzug der additiven Konstante
 der Ausdruck
der Ausdruck  der Newtonschen Mechanik bis auf Größen von der Ordnung
der Newtonschen Mechanik bis auf Größen von der Ordnung 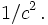 Sehr anschaulich erscheint hierbei die Abhängigkeit der Energie vom Bezugsysteme. Da nun aber die
Sehr anschaulich erscheint hierbei die Abhängigkeit der Energie vom Bezugsysteme. Da nun aber die 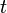 -Achse in die Richtung jedes zeitartigen Vektors gelegt werden kann, so enthält andererseits der Energiesatz, für jedes mögliche Bezugsystem gebildet, bereits das ganze System der Bewegungsgleichungen. Diese Tatsache behält bei dem erörterten Grenzübergang zu
-Achse in die Richtung jedes zeitartigen Vektors gelegt werden kann, so enthält andererseits der Energiesatz, für jedes mögliche Bezugsystem gebildet, bereits das ganze System der Bewegungsgleichungen. Diese Tatsache behält bei dem erörterten Grenzübergang zu  ihre Bedeutung auch für den axiomatischen Aufbau der Newtonschen Mechanik und ist in solchem Sinne hier bereits von Herrn J. R. Schütz[6] wahrgenommen worden.
ihre Bedeutung auch für den axiomatischen Aufbau der Newtonschen Mechanik und ist in solchem Sinne hier bereits von Herrn J. R. Schütz[6] wahrgenommen worden.Man kann von vornherein das Verhältnis von Längeneinheit und Zeiteinheit derart wählen, daß die natürliche Geschwindigkeitsschranke
 wird. Führt man dann noch
wird. Führt man dann noch  an Stelle von
an Stelle von 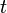 ein, so wird der quadratische Differentialausdruck
ein, so wird der quadratische Differentialausdruck |
also völlig symmetrisch in
 und diese Symmetrie überträgt sich auf ein jedes Gesetz, das dem Weltpostulate nicht widerspricht. Man kann danach das Wesen dieses Postulates mathematisch sehr prägnant in die mystische Formel kleiden:
und diese Symmetrie überträgt sich auf ein jedes Gesetz, das dem Weltpostulate nicht widerspricht. Man kann danach das Wesen dieses Postulates mathematisch sehr prägnant in die mystische Formel kleiden: |
[12]
| Die durch das Weltpostulat geschaffenen Vorteile werden vielleicht durch nichts so schlagend belegt wie durch Angabe der von einer beliebig bewegten punktförmigen Ladung nach der Maxwell-Lorentzschen Theorie ausgehenden Wirkungen. Denken wir uns die Weltlinie eines solchen punktförmigen Elektrons mit der Ladung  und führen auf ihr die Eigenzeit und führen auf ihr die Eigenzeit  ein von irgendeinem Anfangspunkte aus. Um das vom Elektron in einem beliebigen Weltpunkte ein von irgendeinem Anfangspunkte aus. Um das vom Elektron in einem beliebigen Weltpunkte  veranlaßte Feld zu haben, konstruieren wir den zu veranlaßte Feld zu haben, konstruieren wir den zu  gehörigen Vorkegel (Fig. 4). Dieser trifft die unbegrenzte Weltlinie des Elektrons, weil deren Richtungen überall die von zeitartigen Vektoren sind, offenbar in einem einzigen Punkte gehörigen Vorkegel (Fig. 4). Dieser trifft die unbegrenzte Weltlinie des Elektrons, weil deren Richtungen überall die von zeitartigen Vektoren sind, offenbar in einem einzigen Punkte 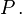 Wir legen in Wir legen in 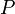 an die Weltlinie die Tangente und konstruieren durch an die Weltlinie die Tangente und konstruieren durch  die Normale die Normale  auf diese Tangente. Der Betrag von auf diese Tangente. Der Betrag von  sei sei  Als der Betrag von Als der Betrag von 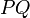 ist dann gemäß der Definition eines Vorkegels ist dann gemäß der Definition eines Vorkegels  zu rechnen. Nun stellt der Vektor in Richtung zu rechnen. Nun stellt der Vektor in Richtung 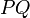 vom Betrage vom Betrage  in seinen Komponenten nach den in seinen Komponenten nach den 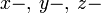 Achsen das mit Achsen das mit  multiplizierte Vektorpotential, in der Komponente nach der multiplizierte Vektorpotential, in der Komponente nach der 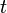 -Achse das skalare Potential des von -Achse das skalare Potential des von  erregten Feldes für den Weltpunkt erregten Feldes für den Weltpunkt  vor. Hierin liegen die von A. Liénard und von E. Wiechert aufgestellten Elementargesetze.[7] vor. Hierin liegen die von A. Liénard und von E. Wiechert aufgestellten Elementargesetze.[7]Bei der Beschreibung des vom Elektron hervorgerufenen Feldes selbst tritt sodann hervor, daß die Scheidung des Feldes in elektrische und magnetische Kraft eine relative ist mit Rücksicht auf die zugrunde gelegte Zeitachse; am übersichtlichsten sind beide Kräfte zusammen zu beschreiben in einer gewissen, wenn auch nicht völligen Analogie zu einer Kraftschraube der Mechanik. Ich will jetzt die von einer beliebig bewegten punktförmigen Ladung auf eine andere beliebig bewegte punktförmige Ladung ausgeübte ponderomotorische Wirkung beschreiben. Denken wir uns durch den Weltpunkt |
[13]
 die Weltlinie eines zweiten punktförmigen Elektrons von der Ladung
die Weltlinie eines zweiten punktförmigen Elektrons von der Ladung  führend. Wir bestimmen
führend. Wir bestimmen  wie vorhin, konstruieren sodann (Fig. 4) den Mittelpunkt der Krümmungshyperbel in
wie vorhin, konstruieren sodann (Fig. 4) den Mittelpunkt der Krümmungshyperbel in  endlich die Normale
endlich die Normale 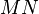 von
von 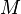 aus auf eine durch
aus auf eine durch 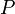 parallel zu
parallel zu  gedachte Gerade. Wir legen nun, mit
gedachte Gerade. Wir legen nun, mit 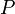 als Anfangspunkt, ein Bezugsystem folgendermaßen fest, die
als Anfangspunkt, ein Bezugsystem folgendermaßen fest, die 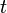 -Achse in die Richtung
-Achse in die Richtung  die
die  -Achse in die Richtung
-Achse in die Richtung 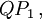 die
die  -Achse in die Richtung
-Achse in die Richtung  womit schließlich auch die Richtung der
womit schließlich auch die Richtung der  -Achse als normal zu den
-Achse als normal zu den 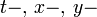 Achsen bestimmt ist. Der Beschleunigungsvektor in
Achsen bestimmt ist. Der Beschleunigungsvektor in 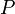 sei
sei  der Bewegungsvektor in
der Bewegungsvektor in  sei
sei  Jetzt lautet der von dem ersten beliebig bewegten Elektron
Jetzt lautet der von dem ersten beliebig bewegten Elektron  auf das zweite beliebig bewegte Elektron
auf das zweite beliebig bewegte Elektron  in
in  ausgeübte bewegende Kraftvektor:
ausgeübte bewegende Kraftvektor: |
wobei für die Komponenten
 des Vektors
des Vektors 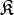 die drei Relationen bestehen:
die drei Relationen bestehen: |
und viertens dieser Vektor
 normal zum Bewegungsvektor in
normal zum Bewegungsvektor in  ist und durch diesen Umstand allein in Abhängigkeit von dem letzteren Bewegungsvektor steht.
ist und durch diesen Umstand allein in Abhängigkeit von dem letzteren Bewegungsvektor steht.Vergleicht man mit dieser Aussage die bisherigen Formulierungen[8] des nämlichen Elementargesetzes über die ponderomotorische Wirkung bewegter punktförmiger Ladungen aufeinander, so wird man nicht umhin können, zuzugeben, daß die hier in Betracht kommenden Verhältnisse ihr inneres Wesen voller Einfachheit erst in vier Dimensionen enthüllen, auf einen von vornherein aufgezwungenen dreidimensionalen Raum aber nur eine sehr verwickelte Projektion werfen.
In der dem Weltpostulate gemäß reformierten Mechanik fallen die Disharmonien, die zwischen der Newtonschen Mechanik und der modernen Elektrodynamik gestört haben, von selbst aus. Ich will noch die Stellung des Newtonschen Attraktionsgesetzes zu diesem Postulate berühren. Ich will annnehmen, wenn zwei Massenpunkte
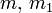 ihre Weltlinien beschreiben, werde von
ihre Weltlinien beschreiben, werde von  auf
auf 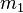 ein bewegender Kraftvektor ausgeübt genau von dem soeben im Falle von Elektronen angegebenen Ausdruck, nur daß statt
ein bewegender Kraftvektor ausgeübt genau von dem soeben im Falle von Elektronen angegebenen Ausdruck, nur daß statt 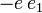 jetzt
jetzt  treten soll. Wir betrachten nun speziell den Fall, daß der Beschleunigungsvektor von
treten soll. Wir betrachten nun speziell den Fall, daß der Beschleunigungsvektor von  konstant Null ist, wobei wir dann
konstant Null ist, wobei wir dann 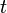 so einführen mögen, daß
so einführen mögen, daß  als ruhend aufzufassen ist, und es erfolge die Bewegung von
als ruhend aufzufassen ist, und es erfolge die Bewegung von 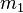
[14] allein mit jenem von
 herrührenden bewegenden Kraftvektor. Modifizieren wir nun diesen angegebenen Vektor zunächst durch Hinzusetzen des Faktors
herrührenden bewegenden Kraftvektor. Modifizieren wir nun diesen angegebenen Vektor zunächst durch Hinzusetzen des Faktors  der bis auf Größen von der Ordnung
der bis auf Größen von der Ordnung 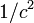 auf 1 hinauskommt, so zeigt sich[9], daß für die Orte
auf 1 hinauskommt, so zeigt sich[9], daß für die Orte  von
von 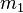 und ihren zeitlichen Verlauf genau wieder die Keplerschen Gesetze hervorgehen würden, nur daß dabei an Stelle der Zeiten
und ihren zeitlichen Verlauf genau wieder die Keplerschen Gesetze hervorgehen würden, nur daß dabei an Stelle der Zeiten 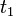 die Eigenzeiten
die Eigenzeiten  von
von 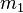 eintreten würden. Auf Grund dieser einfachen Bemerkung läßt sich dann einsehen, daß das vorgeschlagene Anziehungsgesetz verknüpft mit der neuen Mechanik nicht weniger gut geeignet ist, die astronomischen Beobachtungen zu erklären als das Newtonsche Anziehungsgesetz verknüpft mit der Newtonschen Mechanik.
eintreten würden. Auf Grund dieser einfachen Bemerkung läßt sich dann einsehen, daß das vorgeschlagene Anziehungsgesetz verknüpft mit der neuen Mechanik nicht weniger gut geeignet ist, die astronomischen Beobachtungen zu erklären als das Newtonsche Anziehungsgesetz verknüpft mit der Newtonschen Mechanik.Auch die Grundgleichungen für die elektromagnetischen Vorgänge in ponderablen Körpern fügen sich durchaus dem Weltpostulate. Sogar die von Lorentz gelehrte Ableitung dieser Gleichungen auf Grund von Vorstellungen der Elektronentheorie braucht zu dem Ende keineswegs verlassen zu werden, wie ich anderwärts zeigen werde.
Die ausnahmslose Gültigkeit des Weltpostulates ist, so möchte ich glauben, der wahre Kern eines elektromagnetischen Weltbildes, der von Lorentz getroffen, von Einstein weiter herausgeschält, nachgerade vollends am Tage liegt. Bei der Fortbildung der mathematischen Konsequenzen werden genug Hinweise auf experimentelle Verifikationen des Postulates sich einfinden, um auch diejenigen, denen ein Aufgeben altgewohnter Anschauungen unsympathisch oder schmerzlich ist, durch den Gedanken an eine prästabilierte Harmonie zwischen der reinen Mathematik und der Physik auszusöhnen.
H. Minkowski:
Geometrie der Zahlen
In 2 Lieferungen.
I. Lieferung. [240 S.] gr. 8. 1896. Geh. n. M. 8.—
Diese Schrift enthält eine neue Art Anwendungen der Analysis des Unendlichen auf die Zahlentheorie oder, besser gesagt, knüpft ein neues Band zwischen diesen beiden Gebieten. Es werden hier in bezug auf eine Klasse von vielfachen Integralen einige Ungleichheiten entwickelt, die eine fundamentale Bedeutung haben für Fragen über approximative Lösungen von Gleichungen durch rationale Zahlen und für Probleme, welche mit derartigen Fragen zusammenhängen. Im Mittelpunkt der Untersuchung steht ein arithmetisches Prinzip von besonderer Fruchtbarkeit, dessen vielseitige Verwendung auf der Mannigfaltigkeit von Einzelgestalten beruht, die eine nirgends konkave Fläche mit Mittelpunkt darzubieten imstande ist. Das erste Kapitel enthält eine eingehende Begründung der Eigenschaften der nirgends konkaven Flächen. Im zweiten sind einige hier zu verwendende bekannte Sätze aus der Funktionentheorie mit ihren Beweisen dargestellt. Das dritte Kapitel ist der Entwicklung des genannten Prinzips gewidmet. Das vierte bis siebente Kapitel bringt Anwendungen des Prinzips auf die approximative Auflösung von Gleichungen durch rationale Zahlen und durch ganze Zahlen, auf die Theorie der algebraischen Zahlen, auf die Theorie der quadratischen Formen usw., das achte Kapitel endlich eine besondere Untersuchung, die mit jenem Prinzip in loserem Zusammenhange steht. Geometrie der Zahlen ist das Buch betitelt, weil der Verf. zu den Methoden, die die in ihm gegebenen arithmetischen Sätze liefern, durch räumliche Anschauung geführt worden ist. Die vorliegende erste Lieferung enthält bereits die meisten allgemeinen Theoreme, während die in Vorbereitung befindliche Schlußlieferung noch mancherlei Anwendungen bringen wird. |
- ↑ Eine wesentliche Anwendung dieser Tatsache findet sich bereits bei W. Voigt, Göttinger Nachr. 1887, p. 41.
- ↑ A. Einstein, Ann. d. Phys. 17, 1905, p. 891; Jahrb. d. Radioaktivität u. Elektronik 4, 1907, p. 411.
- ↑ M. Planck, Zur Dynamik bewegter Systeme, Berliner Ber. 1907, p. 542 (auch Ann. d. Phys. 26, 1908, p. 1).
- ↑ H. Minkowski, Die Grundgleichungen für die elektromagnetischen Vorgänge in bewegten Körpern, Göttinger Nachr. 1908, p. 53.
- ↑ H. Minkowski, a. a. 0. p. 107. — Vgl. auch M. Planck, Verh. d. Physik. Ges. 4, p. 136, 1906.
- ↑ J. R. Schütz, Das Prinzip der absoluten Erhaltung der Energie. Göttinger Nachr. 1897, p. 110.
- ↑ A. Liénard, Champ électrique et magnétique produit par une charge concentrie en un point et animée d’un mouvement quelconque, L’Éclairage électrique 16 (1898), p. 5, 53, 106; Wiechert, Elektrodynamische Elementargesetze, Arch. néerl. (2), 5 (1900), p. 549.
- ↑ K. Schwarzschild, Göttinger Nachr. 1903, p. 132. — H. A. Lorentz, Enzykl. d. math. Wissensch., Art. V, 14, p. 199.
- ↑ H. Minkowski, a. a. 0., p. 110.
____
Der Vortrag über „Raum und Zeit“, den Hermann Minkowski auf der Versammlung Deutscher Naturforscher und Ärzte zu Köln gehalten hat, bildet die letzte seiner genialen Schöpfungen. Leider ist es ihm nicht beschieden gewesen, den feineren Ausbau seines kühnen Entwurfs einer Mechanik, in welcher die Zeit den drei Dimensionen des Raumes koordiniert ist, zu vollenden. Denn ein tragisches Geschick hat den als Mensch und Forscher gleich geschätzten Verfasser auf der Höhe seines Lebens und Schaffens am 12. Januar d. J. der Wissenschaft, seinen Lieben und Freunden jäh entrissen.
Das verständnisvolle und begeisterte Interesse, das sein Vortrag erweckt hatte, erfüllte Minkowski mit innerer Befriedigung, und er wünschte, seine Darlegungen durch eine Sonderausgabe weiteren Kreisen zugänglich zu machen. Der Verlagsbuchhandlung von B. G. Teubner und dem Unterzeichneten ist es eine schmerzliche Pflicht der Pietät und Freundschaft, diesen letzten Wunsch des Verstorbenen hiermit zu erfüllen.
Halle a. S., den 20. Februar 1909.
A. Gutzmer.





33 Comments:
RAUM UND ZEIT
VORTRAG, GEHALTEN AUF DER 80. NATUR-
FORSCHER-VERSAMMLUNG ZU KÖLN
AM 21. SEPTEMBER 1908
VON
HERMANN MINKOWSKI
MIT DEM BILDNIS HERMANN MINKOWSKIS
SOWIE EINEM VORWORT VON A. GUTZMER
LEIPZIG UND BERLIN
DRUCK UND VERLAG VON B.G.TEUBNER
1909
Raum und Zeit
空間と時間
Oのあちら側
後円錐
時間ベクトル
中間双曲線 O 空間的ベクトル
前円錐
第2図
_______
曲率双曲線 世界線
第3図
:
Oのあちら側
後
円
錐
時間ベクトル
中間双曲線 O 空間的ベクトル
錐
円
前 Oのこちら側
第2図
__________
曲率双曲線 世界線
第3図
:
第2図
ル
Oのあちら側 ト
ク
後 ベ
円 的
錐 間
時
中間双曲線 O 空間的ベクトル
錐
円
前 Oのこちら側
__________
第3図
曲 世
率 界
双 線
曲
線
一見対極に見える、ベルグソンの知覚概念図(円錐)とミンコフスキー時空が似ていると言うことはすでにいろいろな人に指摘されている(http://noos.cocolog-nifty.com/cavesyndrome/2008/07/5023_f540.html)。
____________
参考:
////\ 時間的 ///////
/////\ | ////////
//////\ 未来 /////////
///////\ | //////////
////////\ | ///////////
____ 空間的_\|/_空間的(=物自体)_____
//////////|\///////////
///////// | \//////////
//////// 過去 \/////////
/////// | \////////
////// 時間的 \///////
ミンコフスキー時空図
参照:湯川秀樹『物理講義』
_____________________
/ \
A( )B 記憶の全体、過去
\_____________________/
\ /
\ _______________ / 従来の心理学、哲学で無視されがちな、
A' ( ) B' 精神生活の無数の反復及び、
\_____________/ 無数の切断面
\ /
記憶全体 \ _______ /
A'' (_______)B'' 無数の切断面
\自我の運動 /
_______\ ↑↓ /________P 現実的表象を現す運動平面
/ \ ↑↓ /身体の形象 /
/ \/ /
/ S 現在の知覚 /
/____________________/
ベルクソン『物質と記憶』における知覚と記憶、円錐モデル
______________________
/ \
A( )B 記憶の全体、過去
\______________________/
\ /
\ ________________ / 従来の心理学、哲学で無視されがちな、
A' ( ) B' 精神生活の無数の反復及び、
\______________/ 無数の切断面
\ /
記憶全体 \ _______ /
A'' (_______)B'' 無数の切断面
\自我の運動 /
_______\ ↑↓ /________P 現実的表象を現す運動平面
/ \↑↓ /身体の形象 /
/ \/ /
/ S 現在の知覚 /
/___________________/
ベルクソン『物質と記憶』における知覚と記憶、円錐モデル
:
______________________
/ \
A( )B 記憶の全体、過去
\______________________/
\ /
\ ________________ / 従来の心理学、哲学で無視されがちな、
A' ( ) B' 精神生活の無数の反復及び、
\______________/ 無数の切断面
\ /
記憶全体 \ _______ /
A'' (_______)B'' 無数の切断面
\自我の運動 /
_______\ ↑↓ /_______P 現実的表象を現す運動平面
/ \↑↓/身体の形象 /
/ \/ /
/ S 現在の知覚 /
/___________________/
ベルクソン『物質と記憶』における知覚と記憶、円錐モデル
http://www.amazon.co.jp/dp/B000JA33DC
Amazon.co.jp: 幾何学の基礎をなす仮説について (1970年): リーマン, 菅原 正巳: 本
http://ja.wikipedia.org/wiki/%E3%
『相対論』 物理学史研究刊行会訳・編、東海大学出版会〈物理学古典論文叢書4〉、1969年。 - 「相対性原理」(H.Minkowski著、上川友好訳)、「空間と時間」(H.Minkowski著、上川友好訳)収録。
リーマン 『幾何学の基礎をなす仮説について』 菅原正巳訳、清水弘文堂書房、1970年。 - ミンコウスキー「空間と時間」併録。
Catoni, Francesco; Cannata, Roberto; Catoni, Vincenzo; Nichelatti, Enrico; Zampetti, Paolo (2008). The Mathematics of Minkowski Space-Time: With an Introduction to Commutative Hypercomplex Numbers. Basel: Birkhäuser. ISBN 978-3764386139.
Naber, Gregory L. (1992). The Geometry of Minkowski Spacetime. New York: Springer-Verlag. ISBN 0-387-97848-8. (hardcover), ISBN 0-486-43235-1 (Dover paperback edition).
Walter, Scott (1999). “Minkowski, Mathematicians, and the Mathematical Theory of Relativity”. In Goenner, Hubert et al. (ed.). The Expanding Worlds of General Relativity. Boston: Birkhäuser. pp. 45–86. ISBN 0817640606.
外部リンク [編集]
アニメーション・クリップ - 特殊相対性理論の観点からミンコフスキー空間を視覚化したもの。?
http://www.youtube.com/watch?v=C2VMO7pcWhg
6:36 午後
yoji said...
http://ja.wikipedia.org/wiki/%E3%83%9F%E3%83%B3%E3%82%B3%E3%83%95%
ミンコフスキー空間の名前はドイツの数学者ヘルマン・ミンコフスキーにちなんだものである。ミンコフスキーは1907年ごろに、(アルバート・アインシュタインによって発展させられていた)特殊相対性理論が時間の次元と空間の三つの次元を組み合わせた四次元の時空を用いることで簡素に説明されることを見いだした。
「空間と時間に関し私がここで展開したいと思っている視点は、実験物理学の土壌から芽生えたものであり,その力強さを内に持っている。この視点は革新的なものであり,これからは空間それ自身であるとか時間それ自身であるとかいったような概念は陰にすぎないところへと消え去っていくことになる。そしてこの両者を合わせたもののみが独立した実在としてあり続けることになる。」 – ヘルマン・ミンコフスキー、1908年
1890年代における双曲四元数の発展によりミンコフスキー空間への道が開かれることになった。実際のところ,数学的にはミンコフスキー空間とは双曲四元数の空間から乗法の情報を忘れて双線形形式
η(p,q) = −(pq* + (pq*)*)/2
(これは双曲四元数の積pq*によって定まる)のみを残したものと考えることができる。
6:41 午後
yoji said...
http://www.amazon.co.jp/dp/B000JA33DC
Amazon.co.jp: 幾何学の基礎をなす仮説について (1970年): リーマン, 菅原 正巳: 本
『物質と記憶』 [編集]
その後1896年には、哲学上の大問題である心身問題を扱った第2の主著、『物質と記憶』を発表。ここでベルクソンは失語症についての研究を手がかりに、物質と表象の中間的存在として「イマージュ("image")」という概念を用いつつ、心身関係という哲学上の大問題と格闘している。
すなわち、ベルクソンは、実在を持続の流動とする立場から、心(記憶)と身体(物質)を持続の緊張と弛緩の両極に位置するものとして捉えた。そして、その双方が持続の律動を通じて相互にかかわりあうことを立証した。
一見対極に見える、ベルグソンの知覚概念図(円錐)とミンコフスキー時空が似ていると言うことはすでにいろいろな人に指摘されている(http://noos.cocolog-nifty.com/cavesyndrome/2008/07/5023_f540.html)。
____________
参考:
////\ 時間的 ///////
/////\ | ////////
//////\ 未来 /////////
///////\ | //////////
////////\ | ///////////
____ 空間的_\|/_空間的(=物自体)_____
//////////|\///////////
///////// | \//////////
//////// 過去 \/////////
/////// | \////////
////// 時間的 \///////
ミンコフスキー時空図(『空間と時間』1908年)
_____________________
/ \
A( )B 記憶の全体、過去
\_____________________/
\ /
\ _______________ / 従来の心理学、哲学で無視されがちな、
A' ( ) B' 精神生活の無数の反復及び、
\_____________/ 無数の切断面
\ /
記憶全体 \ _______ /
A'' (_______)B'' 無数の切断面
\自我の運動 /
_______\ ↑↓ /________P 現実的表象を現す運動平面
/ \ ↑↓ /身体の形象 /
/ \/ /
/ S 現在の知覚 /
/____________________/
ベルクソン『物質と記憶』(1896年)における知覚と記憶、円錐モデル
両者に持続("durée")と構造の違い、はある
768夜『不思議の国のトムキンス』ジョージ・ガモフ|松岡正剛の千夜千冊
http://1000ya.isis.ne.jp/0768.html
参考¶『ガモフ全集』は何度かリニューアルされて、いまでも白揚社から全巻が刊行されている。絶対にお買い得。なおごく最近になって、新たな科学理論や最新実験結果を加えたトムキンス物語のヴァージョン・アップがラッセル・スタナードによって試みられて『不思議宇宙のトムキンス』(白揚社)になったり、古川タクのイラストレーションによる『トムキンスさん』(白揚社)になったりしていて、いわば蘇ったホームズ探偵に似た“続編”や“劇画化”がブームになりそうなのだが、どちらも感心しない。古川タクはぼくも好きなイラストレーターの一人ではあるものの、このトムキンス劇画は、まったくつまらなかった。
アインシュタインとボーア :
http://yojiseki.exblog.jp/9732486/
http://pc.nikkeibp.co.jp/article/column/20081209/1010325/
その中でも、宇宙船のランデブーに関する運動の法則は、多くの人が驚くはずである。
地球を回る同じ軌道を、2機の宇宙船が回っているとしよう。前を行く宇宙船に後ろの宇宙機が追いつくためにはどうしたらいいだろうか。
地上の常識に従うならば、「後ろの宇宙機がロケットを噴射して加速して、前を行く宇宙船に追いつく」ということになるだろう。しかし、これは不正解。実際には後ろを行く宇宙機が逆噴射をして減速しなくてはならない。追いつくためにはスピードを落とさなければならないのである。
なぜこんなことになるのかというと、「宇宙船が地球という星の周りを回る軌道に入っている」からだ。
地球を回る軌道では、加速すると宇宙機はより高い軌道に入る。高い軌道は一周するのに必要な周期が長くなる。つまり前に向かって加速すると宇宙船は高い軌道に入って、速度は逆にゆっくりになるのである。逆に減速すると、宇宙機はより低い軌道に入る。地表に近い低い軌道は、周期が短く速度も速い。
だから、先行する宇宙機に追いつきたいならば、逆噴射を行ってちょっと減速しなくてはならない。減速すると軌道高度が下がって速度が上がり、前の宇宙機に追いつくことができる。
地球を回る軌道は、加速すると自動的に上り坂に入って、速度が落ちてしまう奇妙な道というわけだ。逆に減速すると自動的に下り坂に入るわけである。
その結果、「追いつくためにはアクセルを踏まずにブレーキをかけろ」というのが、“宇宙の常識”となるわけである。
[自国のロケットで人工衛星を打ち上げた国]
ミミ;露ミミ | ̄ ̄|
( `,_o´).米米米__
( ).(.´_⊃`)∧仏∧
.| | | ( )ξ・_>・).∧日∧ ∧∧
(__)__)| | | .( )(*´∀`)/中\
| ̄ ̄ ̄|(__)_.)| | | .( )( `ハ´)∧英∧
| | ̄ ̄ ̄|(__)_.)| | | ( )ミ.´_>`)∧欧∧.γ三ヽ
| | | ̄ ̄ ̄|(__)_.)| | | ( )ξ´_U`)(彡印ミ)┏━┓
| | | | ̄ ̄ ̄|(__)_.)| | | ( )( ´,_>`)━━━
| | | | | ̄ ̄ ̄|(__)_.)| | | .( )ミΘoΘミ[.イラン.]ミ
| | | | | | ̄ ̄ ̄|(__)_.)| | | ( ).(.´_U`.) [.北朝.]
| | | | | | | ̄ ̄ ̄|(__)_.)| | | ( )<*`∀´>
| | | | | | | | ̄ ̄ ̄|(__)_.)| | | ( )
| | | | | | | | | ̄ ̄ ̄|(__)_.) ) ./\\ グリグリ
| | | | | | | | | | ̄ ̄ ̄|(__) ヽ__)韓.ハ
| | | | | | | | | | | ̄ ̄ ̄|<`д´;> アイゴ
| | | | | | | | | | | |.∪ ∪ )
|ソビエト.=| | | | | | 欧州 | | | | | ( ( ノ
| ロシア.+ | | | | | | 宇宙 | | | | |_<__<_〉__
|ウクライナ| アメリカ.| フランス | 日本 .|. 中国 .|.イギリス.| 機関 | インド .|イスラエル| イラン .|北朝鮮|.韓国+ロシア.|
| 1957 | 1958 | 1965 | 1970.2| 1970.4| 1971 | 1979 | 1980 | 1988 | 2009 | 2012 | 2013 |
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
[自国のロケットで人工衛星を打ち上げた国]
ミミ;露ミミ | ̄ ̄|
( `,_o´).米米米__
( ).(.´_⊃`)∧仏∧
.| | | ( )ξ・_>・).∧日∧ ∧∧
(__)__)| | | .( )(*´∀`)/中\
| ̄ ̄ ̄|(__)_.)| | | .( )( `ハ´)∧英∧
| | ̄ ̄ ̄|(__)_.)| | | ( )ミ.´_>`)∧欧∧.γ三ヽ
| | | ̄ ̄ ̄|(__)_.)| | | ( )ξ´_U`)(彡印ミ)┏━┓
| | | | ̄ ̄ ̄|(__)_.)| | | ( )( ´,_>`)━━━
| | | | | ̄ ̄ ̄|(__)_.)| | | .( )ミΘoΘミ[.イラン.]ミ
| | | | | | ̄ ̄ ̄|(__)_.)| | | ( ).(.´_U`.) [.北朝.]
| | | | | | | ̄ ̄ ̄|(__)_.)| | | ( )<*`∀´>
| | | | | | | | ̄ ̄ ̄|(__)_.)| | | ( )
| | | | | | | | | ̄ ̄ ̄|(__)_.) ) ./\\ グリグリ
| | | | | | | | | | ̄ ̄ ̄|(__) ヽ__)韓.ハ
| | | | | | | | | | | ̄ ̄ ̄|<`д´;> アイゴ
| | | | | | | | | | | |.∪ ∪ )
|ソビエト.= | | | | | | 欧州 | | | | | ( ( ノ
| ロシア.+ | | | | | | 宇宙 | | | | |_<__<_〉__
|ウクライナ | アメリカ.| フランス | 日本 .|. 中国 . |.イギリス .| 機関 | インド .|イスラエル | イラン . |北朝鮮 |.韓国+ロシア.|
| 1957 | 1958 | 1965 | 1970.2| 1970.4 | 1971 | 1979 | 1980 | 1988 | 2009 | 2012 | 2013 |
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
[自国のロケットで人工衛星を打ち上げた国]
ミミ;露ミミ | ̄ ̄|
( `,_o´).米米米__
( ).(.´_⊃`)∧仏∧
.| | | ( )ξ・_>・).∧日∧ ∧∧
(__)__)| | | .( )(*´∀`)/中\
| ̄ ̄ ̄|(__)_.)| | | .( )( `ハ´)∧英∧
| | ̄ ̄ ̄|(__)_.)| | | ( )ミ.´_>`)∧欧∧.γ三ヽ
| | | ̄ ̄ ̄|(__)_.)| | | ( )ξ´_U`)(彡印ミ)┏━┓
| | | | ̄ ̄ ̄|(__)_.)| | | ( )( ´,_>`)━━━
| | | | | ̄ ̄ ̄|(__)_.)| | | .( )ミΘoΘミ[.イラン.]ミ
| | | | | | ̄ ̄ ̄|(__)_.)| | | ( ).(.´_U`.) [.北朝.]
| | | | | | | ̄ ̄ ̄|(__)_.)| | | ( )<*`∀´>
| | | | | | | | ̄ ̄ ̄|(__)_.)| | | ( )
| | | | | | | | | ̄ ̄ ̄|(__)_.) ) ./\\ グリグリ
| | | | | | | | | | ̄ ̄ ̄|(__) ヽ__)韓.ハ
| | | | | | | | | | | ̄ ̄ ̄|<`д´;> アイゴ
| | | | | | | | | | | |.∪ ∪ )
|ソビエト.= | | | | | | 欧州 | | | | | ( ( ノ
| ロシア.+ | | | | | | 宇宙 | | | | |_<__<_〉__
|ウクライナ | アメリカ.| フランス | 日本 .|. 中国 . |.イギリス .| 機関 | インド .|イスラエル | イラン . |北朝鮮 |.韓国+ロシア.|
| 1957 | 1958 | 1965 | 1970.2| 1970.4 | 1971 | 1979 | 1980 | 1988 | 2009 | 2012 | 2013 |
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
[自国のロケットで人工衛星を打ち上げた国]
ミミ;露ミミ | ̄ ̄|
( `,_o´).米米米__
( ).(.´_⊃`)∧仏∧
.| | | ( )ξ・_>・).∧日∧ ∧∧
(__)__)| | | .( )(*´∀`)/中\
| ̄ ̄ ̄|(__)_.)| | | .( )( `ハ´)∧英∧
| | ̄ ̄ ̄|(__)_.)| | | ( )ミ.´_>`)∧欧∧.γ三ヽ
| | | ̄ ̄ ̄|(__)_.)| | | ( )ξ´_U`)(彡印ミ)┏━┓
| | | | ̄ ̄ ̄|(__)_.)| | | ( )( ´,_>`)━━━
| | | | | ̄ ̄ ̄|(__)_.)| | | .( )ミΘoΘミ[.イラン.]ミ
| | | | | | ̄ ̄ ̄|(__)_.)| | | ( ).(.´_U`.) [.北朝.]
| | | | | | | ̄ ̄ ̄|(__)_.)| | | ( )<*`∀´>
| | | | | | | | ̄ ̄ ̄|(__)_.)| | | ( )
| | | | | | | | | ̄ ̄ ̄|(__)_.) ) ./\\ グリグリ
| | | | | | | | | | ̄ ̄ ̄|(__) ヽ__)韓.ハ
| | | | | | | | | | | ̄ ̄ ̄|<`д´;> アイゴ
| | | | | | | | | | | |.∪ ∪ )
|ソビエト.= | | | | | | 欧州 | | | | | ( ( ノ
| ロシア.+ | | | | | | 宇宙 | | | | |_<__<_〉__
|ウクライナ | アメリカ.| フランス | 日本 .|. 中国 . |.イギリス .| 機関 | インド .|イスラエル | イラン . |北朝鮮 |.韓国+ロシア.|
| 1957 | 1958 | 1965 | 1970.2| 1970.4 | 1971 | 1979 | 1980 | 1988 | 2009 | 2012 | 2013 |
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
[自国のロケットで人工衛星を打ち上げた国]
ミミ;露ミミ | ̄ ̄|
( `,_o´).米米米__
( ).(.´_⊃`)∧仏∧
.| | | ( )ξ・_>・).∧日∧ ∧∧
(__)__)| | | .( )(*´∀`)/中\
| ̄ ̄ ̄|(__)_.)| | | .( )( `ハ´)∧英∧
| | ̄ ̄ ̄|(__)_.)| | | ( )ミ.´_>`)∧欧∧.γ三ヽ
| | | ̄ ̄ ̄|(__)_.)| | | ( )ξ´_U`)(彡印ミ)┏━┓
| | | | ̄ ̄ ̄|(__)_.)| | | ( )( ´,_>`)━━━
| | | | | ̄ ̄ ̄|(__)_.)| | | .( )ミΘoΘミ[.イラン.]ミ
| | | | | | ̄ ̄ ̄|(__)_.)| | | ( ).(.´_U`.) [.北朝.]
| | | | | | | ̄ ̄ ̄|(__)_.)| | | ( )<*`∀´>
| | | | | | | | ̄ ̄ ̄|(__)_.)| | | ( )
| | | | | | | | | ̄ ̄ ̄|(__)_.) ) ./\\ グリグリ
| | | | | | | | | | ̄ ̄ ̄|(__) ヽ__)韓.ハ
| | | | | | | | | | | ̄ ̄ ̄|<`д´;> アイゴ
| | | | | | | | | | | |.∪ ∪ )
|ソビエト.= | | | | | | 欧州, | | | | | ( ( ノ
| ロシア.+ | | | | | | 宇宙 | | | | |_<__<_〉__
|ウクライナ | アメリカ.| フランス | 日本 .|. 中国 . |.イギリス .| 機関 | インド .|イスラエル | イラン . |北朝鮮 |.韓国+ロシア.|
| 1957 | 1958 | 1965 | 1970.2| 1970.4 | 1971 | 1979 | 1980 | 1988 | 2009 | 2012 | 2013 |
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
[自国のロケットで人工衛星を打ち上げた国]
ミミ;露ミミ | ̄ ̄|
( `,_o´).米米米__
( ).(.´_⊃`)∧仏∧
.| | | ( )ξ・_>・).∧日∧ ∧∧
(__)__)| | | .( )(*´∀`)/中\
| ̄ ̄ ̄|(__)_.)| | | .( )( `ハ´)∧英∧
| | ̄ ̄ ̄|(__)_.)| | | ( )ミ.´_>`)∧欧∧.γ三ヽ
| | | ̄ ̄ ̄|(__)_.)| | | ( )ξ´_U`)(彡印ミ)┏━┓
| | | | ̄ ̄ ̄|(__)_.)| | | ( )( ´,_>`)━━━
| | | | | ̄ ̄ ̄|(__)_.)| | | .( )ミΘoΘミ[.イラン.]ミ
| | | | | | ̄ ̄ ̄|(__)_.)| | | ( ).(.´_U`.) [.北朝.]
| | | | | | | ̄ ̄ ̄|(__)_.)| | | ( )<*`∀´>
| | | | | | | | ̄ ̄ ̄|(__)_.)| | | ( )
| | | | | | | | | ̄ ̄ ̄|(__)_.) ) ./\\ グリグリ
| | | | | | | | | | ̄ ̄ ̄|(__) ヽ__)韓.ハ
| | | | | | | | | | | ̄ ̄ ̄|<`д´;> アイゴ
| | | | | | | | | | | |.∪ ∪ )
|ソビエト.= | | | | | | 欧州 | | | | | ( ( ノ
| ロシア.+ | | | | | | 宇宙 | | | | |_<__<_〉_
|ウクライナ | アメリカ.| フランス | 日本 .|. 中国 . |.イギリス .| 機関 | インド .|イスラエル | イラン . |北朝鮮 |.韓国+ロシア.|
| 1957 | 1958 | 1965 | 1970.2| 1970.4 | 1971 | 1979 | 1980 | 1988 | 2009 | 2012 | 2013 |
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
【宇宙】ブラックホールに落ち込む最後の1/100秒の解明へ ガスが最後に放つ高エネルギーX線を初めて捉えた!/理研など
1 :白夜φ ★:2013/04/05(金) 00:50:21.09 ID:???
2013年4月4日
独立行政法人理化学研究所
国立大学法人京都大学
学校法人日本大学
国立大学法人東京大学
ブラックホールに落ち込む最後の1/100秒の解明へ
-ガスが最後に放つ高エネルギーX線を初めて捉えた!-
強力な重力のため、光さえも飲み込んでしまうという暗黒の天体「ブラックホール」は、実在するのでしょうか?
状況証拠こそ集まってきたものの、じつは今でも、直接的な観測証拠はありません。
1971年、今から40年ほど前に「はくちょう座X-1」という、X線で明るく光る不思議な天体が発見されました。
X線強度が秒以下の短い時間で変動することや、太陽の数倍以上の質量を持つこともわかりました。
短い時間でX線が変動することは、X線を出す領域、すなわち天体が極めて小さいことを意味します。
こうして、「はくちょう座 X-1」 はブラックホール候補天体となりました。
はくちょう座X-1は連星系の中にあります(図)。
ブラックホールは、連星系の相手の恒星の周囲のガスを引き込みます。
引き込まれたガスはブラックホールの周りをぐるぐる回る円盤をつくり、最終的にブラックホールに落ち込みます。
ガスは、ブラックホールに落ち込む時高温になりX線を出します。
このX線をうまくキャッチすることにより、ブラックホールの周囲を詳しく“観察” できるのです。
理研の研究者らは、X線観測衛星「すざく」に搭載された高感度の「硬X線検出器」を用い、
「重ね合わせショット解析」というX線強度や色(波長)の細かな変動が測定できる独自の手法を適用し、
ガスがブラックホールに落ち込む最後の100分の1秒間に10億度以上まで急激に加熱されることを発見しました。
もし中心天体に表面があれば、表面からの放射がガスを冷やすため今回の観測を説明できません。
したがって本観測は、中心に「表面のない天体」、つまりブラックホールがあることを意味します。
ブラックホール存在の直接証明に一歩近づいた成果といえます。
----------------
独立行政法人理化学研究所
仁科加速器研究センター 玉川高エネルギー宇宙物理研究室
基礎科学特別研究員 山田 真也 (やまだ しんや)
_________________
▽記事引用元 理化学研究所 60秒でわかるプレスリリース 2013年4月4日
http://www.riken.go.jp/pr/press/2013/20130404_2/digest/
「はくちょう座 X-1」 ブラックホール連星の想像図
http://www.riken.go.jp/~/media/riken/pr/press/2013/20130404_2/digest.jpg
プレスリリース 報道発表資料
http://www.riken.go.jp/pr/press/2013/20130404_2/
http://ja.wikipedia.org/wiki/%E3%82%AA%E3%83%BC%E3%83%AC%E3%83%BB%E3%83%AC%E3%83%BC%E3%83%9E%E3%83%BC
オーレ・レーマー
オーレ・クリステンセン・レーマー
オーレ・クリステンセン・レーマー (1735年)
人物情報
生誕 1644年9月25日
デンマーク=ノルウェー デンマーク オーフス
死没 1710年9月19日
デンマーク=ノルウェー デンマーク コペンハーゲン
国籍 デンマーク
学問
研究分野 天文学
研究機関 コペンハーゲン大学
主な業績 光速度
テンプレートを表示
オーレ・クリステンセン・レーマー(Ole Christensen Rømer、1644年9月25日 – 1710年9月19日)はデンマークの天文学者。1676年に、科学的に意味のある光速度の値を世界で初めて算出した。1681年からコペンハーゲン大学で数学の教授を務めた。
イタリアの天文学者・ジョヴァンニ・カッシーニの観測した木星の衛星のイオの食が早まる変動が、木星から地球(観測者)に光が到達する時間の差によるものとして、カッシーニのデータを使って光の速度を計算した。
1676年9月に計算を行い、11月には逆にイオの食が計算通り遅れることが観測により確認された。
地球と太陽の距離は光速で500秒ぐらいで、太陽と木星の距離は5.2AU(天文単位)なので、地球と木星の距離は太陽の同じ側にある場合光速で2000秒(30分)位である。地球が木星に近づいていく場合(概算で1日に光速で10秒ぐらいの距離ずつ近づく計算になる)には、光が地球に到達するまでにかかる時間がしだいに短くなり、それに従って食の起きる間隔も短くなる。天体間の距離、速度を知れば逆に光速を見積もることができる。 このようにして計算された光速度は、メートル法に直すと214300km/sであった。
また、1702年には水の融点と沸点を元に独自の温度計を製作。現在ではレーマー度と呼ばれている。小惑星(3455)のクリステンセンは、彼の功績を称えて命名された。なお、彼の肖像はデンマークの旧50クローネ紙幣に描かれていた。
カテゴリ: デンマークの天文学者17世紀の学者コペンハーゲン大学の教員オーフス出身の人物ヨーロッパの紙幣の人物1644年生1710年没
アンドロメダ
250万年前
ケンタウロス
1000万年前
NGC50
一億光年
太陽
8分
ハイデガーはミンコフスキーについてカッセル講演、邦訳109頁で言及している。
かくして、バーバーによれば、ニュートンとライプニッツの争いは次のように調停される。
これにより、絶対運動と相対運動について論争したニュートンとライプニッツの立場の間で、意外な調停がもたらされた。どちらも正しかったのである! 要点は、われわれの宇宙のように多くの物体を含む宇宙においては、互いに他から事実上切り離された部分系が無数にありうるということである。[中略]各々の部分系は、それだけを考えると、ゼロでないエネルギーと角運動量をもちうる。しかし、宇宙が有限であれば、その部分系の個々のエネルギーと角運動量を加え合わせていくとゼロとなりうる。ニュートンの諸法則によって支配されている宇宙では、そうなることはありそうにない偶然であろう。しかし、宇宙がマッハ的法則に支配されているのであれば、そうなることは必然である。それはこの法則の直接の帰結である。さらに、マッハ的法則によれば、大きな宇宙においては、すべての十分に孤立した部分系は、まさにニュートンが予測したように振る舞うであろうという予測が出てくる。とくに、そのような部分系はゼロでないエネルギーと角運動量をもつことができ、それゆえ絶対空間と絶対時間においてニュートンの法則に従っているように見える。ところが、ニュートンにとっては不変の絶対的な枠組みに見えたものが、マッハ流の理論では宇宙全体とそれを支配する一つの法則からの結果にすぎないということを示せるのである。(Barbour 2000, 119)
内井168~9頁
プラトニア(ライプニッツィアーナ 160頁)
BC+CA=AB
________________________
\ l /
\ /
\ /
\ /
\ /
CA+AB=BC\/ \/AB+BC=CA
\ /
\ /
\ /
\ /
\ /
\/
プラトニアの切り口が正三角形の面は三角形の可能なすべての形(寸法は無視)を表せるスペースである。
形空間における軌跡 160頁
(AB)
|
|
|____
/ (CA)
(BC)
参考:
http://d.hatena.ne.jp/sakstyle/20140119/p1
内井惣七『空間の謎・時間の謎』
________________________
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\/
ライプニッツとニュートンの争いは、現代でも決して単なる歴史のエピソードや他人事ではないのである。159頁
…現代の「ストリング(ひも)理論」の発想は、ライプニッツが晩年にたどり着いた思想の再現にほかならない。いまから三〇〇年も前にこのような発想をしていたとは、まさに「ライプニッツおそるべし!」81頁
…現代の「ストリング(ひも)理論」の発想は、ライプニッツが晩年にたどり着いた思想の再現にほかならない。いまから三〇〇年も前にこのような発想をしていたとは、まさに「ライプニッツおそるべし!」81頁
参考:
時間の終わり
ジュリアン・バーバー 邦訳なし
Amazon.co.jp: The End of Time: The Next Revolution in Our Understanding of the Universe: Julian B. Barbour: 洋書
http://www.amazon.co.jp/The-End-Time-Revolution-Understanding/dp/0753810204
参考:
////\ 時間的 ///////
/////\ | ////////
//////\ 未来 /////////
///////\ | //////////
////////\ | ///////////
____ 空間的_\|/_空間的(=物自体)__
//////////|\///////////
///////// | \//////////
//////// 過去 \/////////
/////// | \////////
////// 時間的 \///////
ミンコフスキー時空図
参照:湯川秀樹『物理講義』
https://www.amazon.co.jp/dp/4480095837/
幾何学の基礎をなす仮説について (ちくま学芸文庫) 文庫 – 2013/11/6
ベルンハルト リーマン (著), Bernhard Riemann (原著), & 1 その他
5つ星のうち 5.0
新品
¥ 1,080
商品の説明
内容紹介
相対性理論の着想の源泉となった、リーマンの記念碑的講演。ヘルマン・ワイルの格調高い序文・解説とミンコフスキーの論文「空間と時間」を収録。
内容(「BOOK」データベースより)
H.ワイルの解説で読み解くリーマン幾何学の構想。ミンコフスキー「空間と時間」併収。
商品の説明をすべて表示する
登録情報
文庫 142ページ
出版社: 筑摩書房 (2013/11/6)
言語: 日本語
https://www.amazon.co.jp/dp/4480095837/
幾何学の基礎をなす仮説について (ちくま学芸文庫) 文庫 – 2013/11/6
ベルンハルト リーマン (著), Bernhard Riemann (原著), & 1 その他
5つ星のうち 5.0
新品
¥ 1,080
商品の説明
内容紹介
相対性理論の着想の源泉となった、リーマンの記念碑的講演。ヘルマン・ワイルの格調高い序文・解説とミンコフスキーの論文「空間と時間」を収録。
内容(「BOOK」データベースより)
H.ワイルの解説で読み解くリーマン幾何学の構想。ミンコフスキー「空間と時間」併収。
商品の説明をすべて表示する
登録情報
文庫 142ページ
出版社: 筑摩書房 (2013/11/6)
言語: 日本語
小松左京 「ゴルディアスの結び目」|ジャズと映画と娯楽小説
http://soe006.com/novel.php?no=050518
「ゴルディアスの結び目」(「渦」に関する一行メモ)
要塞のような病院に、マリア・Kという可憐な少女が収容されている。
鋭い牙と頭部に角状の突起物を生やした少女には、邪悪な存在が憑依しており、鉄のバンドで身体を拘束されているにもかかわらず、騒霊現象(ポルターガイスト)を起こし、病室内をメチャクチャに破壊する。
精神分析医が少女の深層心理に侵入し、"憑きもの"の正体に迫るが、病室は大音響とともに内部に向かって崩壊し、収縮しはじめた。
その理由や内部の物理的構造、一切の情報が解明されないまま、かつて「マリアの部屋」と呼ばれていた病室は収縮を続け、やがてマイクロ・ブラック・ホールへと成長してゆく。
5:34 午前 削除
Blogger yoji さんは書きました...
小松左京
ゴルディアスの結び目
「想像力は?ーーミンコフスキイという 、歴とした理論数学者がいてね 。彼の空間論は 、現代科学に大きな貢献をしたが 、反面 、彼は四次元空間について 、妙な事を考えた 。霊体だけが 、この空間に滲透できる 、と言うんだ 。 ─ ─ニュ ートン 、ライプニッツはじめ 、すぐれた理論学者は 、同時に奇妙な神秘思想も抱きやすい 。ミンコフスキイの考えも 、彼の正統的業績からすれば 、とるにたらぬ妄想にすぎないだろうが 、こういう所では 、 〝妄想 〟さえも 、その効果をためしてみたくなる … … 。アレキサンダ ーではないが 、ほどこうとしてほどけない 〝ゴルディアスの結び目 〟にたちむかったら 、たとえ乱暴と思われるやり方でも 、ためしてみるまでさ 。 ─ ─さあ 、行こう 、マリア … … 」
コメントを投稿
<< Home