乗数効果

参考：

リチャード・カーン（Richard Ferdinand Kahn、Baron Kahn、1905 - 1989）

https://nam-students.blogspot.com/2019/06/richard-ferdinand-kahnbaron-kahn1905.html

ミッチェル2019#15:231

乗数プロセス：
　　　　　　┏━━━━━┓　　　　　　　　　┏━━━━┓
　支出変化➡︎┃総需要拡大┃➡︎実質ＧＤＰ上昇➡︎┃雇用拡大┃
　　　　　　┗━━━━━┛　　　　　　　　　┗━━━━┛
　　　誘発的消費拡大　↖︎　┏━━━━━━┓　↙︎賃金他支払い
　　　　　　　　　　　　　┃国民所得拡大┃
　　　　　　　　　　　　　┗━━━━━━┛
　　　　　　　　　　　　　　　　　⬇︎
　　　　　　　　　　　　　　税収、貯蓄、輸入増加

乗数プロセス
需要拡大が生産拡大と所得拡大を引き起こし、さらにそこから新しい需要が生じる。その結果、経済全体の需要・生産・所得が雪だるま式に増えていくプロセスです

15.8 Impact of a change in government spending on equilibrium expenditure and income 233

Aggregate Demand – part 7 (final) – Bill Mitchell – Modern Monetary Theory

2012/10/5

http://bilbo.economicoutlook.net/blog/?p=21197 7/7

15.8 Impact of a change in government spending on equilibrium expenditure and income 233

…

Figure 8.11 The multiplier flow map

:書籍版未使用

15:231

Figure 8.9 The multiplier process
Aggregate Demand
Employment rises
Change in Expenditure
Real GDP rises
rises
Wage and other
Induced
spending
rises
National payments
income rises
Taxes, saving and imports rise

917 金持ち名無しさん、貧乏名無しさん (ｽﾌﾟﾌﾟ Sdd7-QaAb)[sage] 2019/06/06(木) 14:04:34.95  ID:+PL5pbPrd 

>>916

国債が実質的に政府紙幣なんで、敢えて政府紙幣にする必要がないし、

国債廃止の方向で言うならただ単に政府預金のマイナス残高許容で事足りるから、

敢えて政府紙幣にする意味がないんだよねえ。

918 金持ち名無しさん、貧乏名無しさん (ﾜｯﾁｮｲ 31ad-K3Ee)[] 2019/06/06(木) 14:07:57.27  ID:9z75kD270 

>>917

そうそう、すごく的確なこと言った。国債って仕組をよく見ると政府紙幣と同じじゃね？ってのが肝なんだけど

国債だと名目上「国の借金」があって、そこに破綻論者が群がるわけで

まず政府紙幣で思考実験をすると、残るのはインフレ率の抑制のみになる

そのうえで政府紙幣と国債って、片方の手段が迂遠なだけでやってること同じじゃねって話の順番の方が

不毛な財政破綻論がなくなりそうな気がする。残るのはインフレ抑止の方法論だけになるというか

マルクスが推奨したのは生産協同組合

分配を国家に頼ることなく生産現場でするのが理想

MMTは国家に頼るからマルクス主義から見たら妥協

しかもMMT国家も対外的には国家資本主義だから貿易戦争は終わらない

ミッチェルの新刊がケインズの超国家通貨案バンコールに言及しているのは慧眼

乗数分析

https://www2.kumagaku.ac.jp/teacher/~sasayama/macroecon/lecture08.html

政府が公共投資を増加したり，あるいは企業が投資を
増加させることによって，国民所得は増加することが
予想されますが，それはどの程度増加するのであろうか．
あるいは，そのメカニズムはどうなっているのかを探
るのが乗数分析のねらいです．
経済的な波及メカニズム（乗数の考え方）
（例）パソコンの需要増大が経済全体の景気に与える効果
パソコンが５０億円余分に売れたとします
→メーカーは５０億円余分に生産し販売します
→売上増加の５０億円は従業員の賃金の増加や利潤の
増加として５０億円の所得増加をもたらします．
（ここまでが自立的需要増加）
経済への波及効果は上だけに留まりません．
所得の増加したパソコンメーカーの従業員は，所得増加
の一部をその他の消費財（洋服，旅行，外食など）への
支出に向けます．
それらを生産している企業の生産も増大し，そこで働
いている従業員の所得も増加します．
従ってこれらの従業員も様々な商品を購入するので，
さらにその他の企業の生産も増大します．
このような循環が際限なく繰り返されるのです．
（この部分を派生需要の増加といいます）
投資乗数[top]
単純な経済モデル　　財市場の均衡式　　Ｙ＝ C + I 　 　（１）
　　消費関数　　　　　C = Co + c Y 　 （２）
　　投資支出　　　　　 I = Io 　　　　（３）
　　　　　　モデルの図式


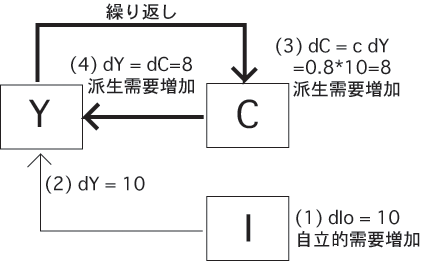
自立的需要の増加（上の図ではdIo=10, c =0.8 ）
　→それに見合った生産の増加→所得の増加（dIo = dＹ）
派生需要の増加：
上で生じた所得増加によってもたらされる需要の増加
　　＝限界消費性向×所得増加
派生需要は無限に近く繰り返されます．
最終的な需要（所得）の増加
＝自立的需要増加＋派生需要の合計＝10 ＋（0.8*10 ＋0.8^2*10 ＋0.8^3*10 +　．．　＋　
　　+ 0.8^n*10＋．．）
= 10( 1 + 0.8 + 0.8^2 + 0.8^3 + 　・・+ 0.8^n +
　　+ ．．．）
（　　）内は初項１，公比０．８の無限等比数列
= 10 ( 1 / (1 - 0.8) ) 　（公式　初項/(1 - 公比）から）
= 10 ×5 = 50
一般的に記号で書くと，
＝dIo ＋（ｃdIo ＋ｃ^２dIo ＋ｃ^３dIo ＋　．．　＋
　　　＋ｃ^ｎdIo＋．．）
＝dIo （１＋ｃ＋ｃ^２＋ｃ^３＋．．．＋ｃ^ｎ＋．．．）

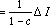
上で（　　）内は初項１，公比ｃの無限等比数列
【公式】無限等比級数の和＝初項／（１ー公比）
（注）無限等比数列の和の公式は，
以下の「高校数学の復習：等比数列」の項目を参照してください．
（重要）
　　　　　　自立的支出増加
所得増加＝ ---------------------
　　　　　 １－限界消費性向
　限界消費性向＝消費の増加分／所得の増加分
　０＜限界消費性向＜１
dIo ＝10，ｃ＝0.8ならば，このときの最終的な需要
増加額は
dY = 10/(1 - 0.8) = 50
１０億円の初期需要の増加によって，最終的には
その５倍の５０億円の所得増加を経済全体にもたら
します．
この倍数のことを乗数と呼びます．この例では
乗数は５となります．
式による求め方
乗数は，均衡所得を求めることから得られることを
示しましょう．
（２）と（３）を（１）に代入し，
Yについて解くと均衡所得が得られます．
　Y = Co + cY + Io
　Y = cY + Co + Io
　(1-c)Y = Co + Io
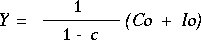　　　　　　　（４）
ここで，上のモデルの（３）式の投資がdIoだけ増加
したとしましょう．すると，
財市場の均衡式　　Ｙ＝ C + I 　 　（１）
消費関数　　　　　C = Co + c Y 　 （２）
投資支出　　　　　 I = Io + dIo　　（３'）
均衡所得の求め方は，（２）と（３’）を（１）に
代入してＹについて解きます，
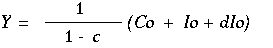　　　（５）
（５）-（４）が所得の増加を表します．
所得の増分をdYとかくと，
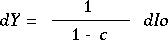　　　　　　　　　　（６）
実は，（４）式の係数部分，
1/(1-c) が乗数の値に等しくなっているのです．
（別解）（６）式を得るにはもっと簡単な方法があります．
最初の均衡所得の式（４）を元に考えます．
（４）式で変化する部分だけを取り出せばいいのです．
変化した部分の記号にはｄという記号を頭につけます．
例えば，Ｙが変化した部分はｄＹと書きます．
ｄＹでひとまとまりの記号です．
投資 Io だけが増加した場合，それによって影響を
受けるのは左辺のＹです．
右辺の係数 1/(1-c) はそのまま付きます．従って，
変化した記号ｄをつけて書けば，
（６）式のようになるのです．
●（重要）
限界消費性向が大きければ大きいほど，乗数は大きい．
所得の増加のうち，消費に振り向けられる割合（限界消費性向）
が大きければ大きい程，追加的に支出される消費需要が
大きくなるので，派生需要の合計もその分大きくなるからです．
---------------------------------------------------
政府支出乗数[top]
政府を追加した経済モデル財市場の均衡式　　Ｙ＝ C + I + G（7）
消費関数　　　　　C = Co + c Yd （8）
投資支出　　　　　 I = Io 　　　　（9）
政府支出　　　　　G = Go　　　（10）
税収　　　　　　　T = To　　　（11）
可処分所得　　　　Yd = Y - T　（12）
　　　　　　　　モデルの図解

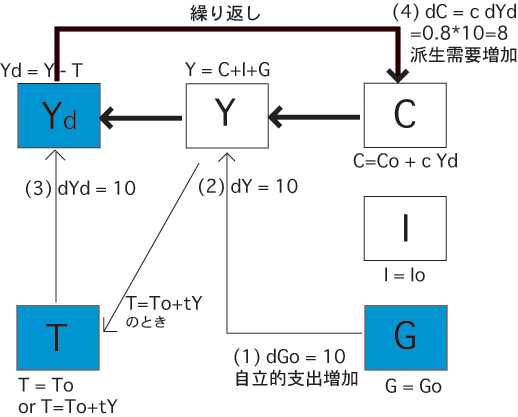
上のモデルの場合，
均衡所得は（（８）から（12）を（７）に
代入してＹについて解きます），
　Y = Co + cYd + Io + Go
　Y = Co + c(Y - To) + Io + Go
　Y - cY = Co - cTo + Io + Go
　(1-c)Y = (Co - cTo + Io + Go)
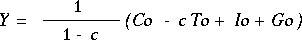　　（13）
政府支出がdGoだけ増加すると，所得の増加は上式から，
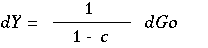　　　　　（14）
政府支出乗数は1/(1-c)です．
租税乗数[top]
減税の乗数効果を分析してみましょう．
モデルは政府支出乗数と同じモデルを使います．
従って，均衡所得は（13）式です．
減税の場合はToの部分だけが変化します（-c dTo）．
従って，
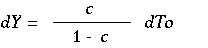　　　　　　　　（15）
租税乗数はc/(1-c)となります．政府支出乗数に
比べると小さくなります．なぜでしょうか？
政府支出の場合は，最初にdGoの増加の効果が現れます．
ところが減税の場合は，まず可処分所得の増加と
なって現れ，可処分所得のうち限界消費性向分だけ
の消費増加が最初の所得増加となって現れます．
第１回目の所得増加から差がついているのです
（モデルの図解参照）．
○ビルト・イン・スタビライザー(built-in stabilizer)
景気がよいときは税収が増えて，これが景気の過熱を
冷まし，
他方，景気が悪化したときは税収が低下することで
（減税の効果）景気回復を助けることになります．
このように税収には自動的に景気を安定化させる機能
をもっています．
これを税収がもつビルト・イン・スタビライザーと
いいます．
均衡予算乗数[top]
政府が均衡予算を維持するように財政支出を増加させ
たときの乗数効果はどうなるか，というのが問題意識．
ここで，均衡予算とは政府の支出はすべて税収に
よって賄う，すなわち赤字国債は発行しないことを
意味します．
従って，例えば１兆円の政府支出を実行するには
１兆円の増税によってまかなわれます．
１兆円の政府支出は１兆円の増税によって完全に
相殺されて，乗数効果はゼロになるのでしょうか．
実は「均衡予算乗数は１である」というのが解答です．
証明は，政府支出乗数と租税乗数を総合すればいいのです．
このとき均衡予算なのでdGo=dToを前提とします．
また，今回は減税ではなく増税なので租税乗数の符号は
マイナスになることにも注意しましょう．
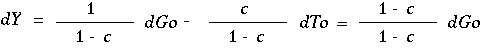　（16）
日経新聞のコラムの筆者は，均衡予算乗数のことを
大学で勉強しなかったわけですね（練習問題集の【問題９】を参照．
以下の「新聞記事の誤りを見つけよう」も参照）．
均衡予算であっても政府支出の増加分だけはGDPの増加
となって現れるのです．
外国貿易乗数[top]
開放経済モデル財市場の均衡式　　Y = C + I + G + EX - IM （17）
消費関数　　　　　C = Co + c Yd 　　（18）
投資関数　　　　　 I = Io 　　　　　　（19）
政府支出　　　　　G = Go 　　　　　　（20）
輸出　　　　　　 EX = EXo 　　　　 　（21）
輸入関数　　　　 IM = IMo + m Y 　　（22）
可処分所得　　　 Yd = Y - T 　　　　 （23）
税収　　　　　　　T = To　　　　　　（24）

http://www.kabu-gakkou.com/2005/11/post_88.html

・インフレーション

物価が上がり続ける状態のこと、つまり、お金の価値が減り続ける状態のことをいう。

インフレが起こる2つの代表的な要因

1.需要が物価を引っ張り上げるインフレ

下図は需要拡大の乗数プロセスを表わしたものです。

では、ここから需要拡大と物価の関係を見ていきましょう。

このように拡大する需要に生産が追いつける間は物価に変動はありません。

しかし、拡大する需要に生産が追いつかなくなると・・・

⇔分、需要が供給を上回り超過需要となり、▲分の総余剰を失うことになります。

つまり、経済的にムダが発生するのです。ゆえに、市場はこのムダを解消するため、物価を引き上げるのです。

2.生産コストが物価を押し上げるインフレ

例）石油価格が上昇（米国：影響大、日本：影響小）

⇔分、需要が供給を上回り超過需要となり、▲分の総余剰を失うことになります。

つまり、経済的にムダが発生するのです。ゆえに、市場はこのムダを解消するため、物価を引き上げるのです。

このように一口にインフレと言っても、さまざまな原因があるのです。当然、そこから得られる結果も違ってきます。インフレが起こった場合、それが何によるものなのかを調べることが大事なのです。

Theory

http://bilbo.economicoutlook.net/blog/?p=21048
https://i1.wp.com/bilbo.economicoutlook.net/blog/wp-content/uploads/2012/09/Figure_8_9_multiplier_schema.jpg

乗数効果：

　　　　　　┏━━━━━┓　　　　　　　　　┏━━━━━┓

内生的変化➡︎┃総需要上昇┃➡︎実質ＧＤＰ上昇➡︎┃雇用率上昇┃

　　　　　　┗━━━━━┛　　　　　　　　　┗━━━━━┛

　　　　　内需拡大　↖︎　　┏━━━━━━━┓　↙︎賃金他支払い

　　　　　　　　　　　　　┃国民所得の増加┃

　　　　　　　　　　　　　┗━━━━━━━┛

　　　　　　　　　　　　　　　　　⬇︎

　　　　　　　　　　　　　　税収、貯蓄、輸入増加

私は今、金曜日のブログスペースを使って、同僚で友人のRandy Wrayと書いている現代通貨理論の教科書のドラフト版を提供しています。 私たちは今年の終わりまでにこのテキストを完成させる予定です。 コメントはいつでも大歓迎です。 これは学部生を対象とした教科書なので、執筆は私のいつものブログとは違ったものになるでしょう。 また、私が投稿したテキストは最初のドラフトとして私が行っている作業であり、投稿された資料は完全なテキストを表すものではありません。 さらに私たち二人がそれを編集したらそれは変わります。 

このブログを先週の続き - 総需要 - 第4部（リデックス） - の続きとして読んでください。この章では、この章の内容の編集内容の統合を図っています。

[私たちが先に離れたところどこかに拾います]

第4章で学んだテクニックを使って、式（8.12）を修正することができます。

（8.13）E = C 0 + I + G + X + [c（1 - t） - m] Y

総需要の自律的なすべての要素（A = C 0 + I + G + Xなど）を集めて総需要関数を次のように書くことで、この式を簡単に整理できます。

（8.14）E = A + [c（1 - t） - m] Y

この関数の傾き - ΔE/ΔY= [c（1 - t） - m] - は、国民所得の一定の変化に対する総支出の変化が大きいほど、消費の限界傾向が大きいことを示します。そしてより低いものは税率（t）と限界輸入傾向（m）である。

この時点でこの結果を自分自身に説明できるかどうかを確認してください。 国民所得が上昇すると消費の限界的な傾向が誘発される消費支出の増加につながると考えてください。税率と輸入の限界的な傾向は国民所得の各ドルの支出システムからの漏洩である。 次のセクションで、 支出の乗数を検討するときに、このことの完全な分析を提供します。

図8.5は、総需要関数とその個々の構成要素を示しています。 関数の切片を取得するために、すべての自律支出項目を追加します。

総需要関数は、横軸に国内生産高/収入、縦軸に総需要または計画支出を用いて描かれている。

それは国民所得と計画支出の間の関係を示しており、2つの側面が重要です。

• 総自律支出 - 水平インターセプト。 そして
• 限界消費傾向（c）、限界消費傾向（m）、および税率（t）に依存する関数の傾き。 そして輸入の限界傾向（m）。

自律的支出を構成する要素のいずれかまたは勾配が変化した場合、総需要（計画支出）は国民所得のあらゆるレベルで変化します。

図8.5を参照すると、計画的な政府支出または民間投資が増加すると、総需要関数は上方にシフトします。垂直方向の切片は計画的支出の増加によって上昇します。 その結果、各支出レベルで計画支出が高くなります。 例えば、政府支出が削減された場合、反対のことが起こります。

図8.6は、A 0からA 1への自律的支出の増加の影響を示しています。

総需要関数もその傾きを変えることができる。 限界消費性向（c）の上昇および/または税率の低下（t）および/または輸入限界性向の傾向（m）は、関数の傾きを大きくするでしょう。

図8.7は限界消費性向の上昇の影響を示している（c）。 すべての国民所得レベルで、計画された支出は現在より高いです。

影響をスケッチし、税率（t）の上昇、輸入の限界性向の上昇（m）、限界の消費性向の低下（c）の意味を説明できるかどうかを確認します。

また、現実の世界では、消費の限界傾向（c）と輸入の限界傾向（m）の実際の値にどの要因が影響するのかを明確にするようにしてください。 例えば、基本的な金融システムを持っている貧困層は、可処分所得が高く、クレジットへのアクセスが広く行き渡っている国よりも、消費する限界性向が高いと予想されるかもしれません。

均衡国民所得

マクロ経済学における均衡という用語は、現在の支出、産出および国民所得の水準を変えるような力が存在しない状況を指すのに使用されます。 その時点で、企業は計画された支出に対する彼らの期待に基づいて彼らが生み出したすべてのアウトプットを売っています。

均衡と完全雇用を混同しないように十分注意してください。 第10章で学ぶように、非自発的失業率が非常に高い場合には、マクロ経済的均衡が生じる可能性があります。完全雇用は、均衡の唯一の可能性のあるポイントです。

均衡は、計画支出が国民の所得と産出に等しいときに生じる。

経済における企業は量的調整者であり、短期的には価格は固定されているという我々の現在の仮定の下で、図8.1は45 0ラインが総供給曲線であることを示した。 各時点で、企業は自分たちの期待を認識し、市場に実際の生産量を供給するという彼らの決定を批准しています。 批准は、それらの費用の総計と希望する利益量の両方をカバーする予想収入の受け取りによってもたらされます。

企業が膨大な量のアウトプットを展開するために利用できるアイドルリソースがあると暗黙のうちに想定しています。 ある時点で、経済がフル稼働しているとき、企業は追加支出に対応して実質生産高を拡大し続けることができない。 その時点で、価格の上昇は避けられません。

したがって、この時点で総需要関数が45 0ラインをカットしたときに均衡が生じ、企業が供給を決定する動機となった総需要予測（Y * ）が消費者による計画支出（E *）と一致する。企業、政府そして対外経済。

図8.8は、均衡所得（Y * ）と支出（E * ）の組み合わせを示しています。 第7章で使用されている用語では、この時点でこの時点での経済における実効需要が定義されます。

Aggregate Demand Functionと45 0行の間にある2つの領域に注意してください。 エリアA（ゾーンA）は、計画された支出が予想される需要より大きく、したがって実際の生産高と収入であることを特徴としています。 企業は実際の計画支出と一致するであろうよりも生産高を過少供給し、より少ない国民所得を生み出した。

このような状況では、計画外の在庫切れは企業が彼らの期待に誤っていたというシグナルを提供します。 企業は、生産量と国民所得を増加させることによって、この予定外の在庫の減少に対処するでしょう。

同様に、エリアB（ゾーンB）は、計画支出が予想需要より少なく、したがって実際の生産高と収入であることを特徴としています。 企業は楽観的過ぎ、過剰供給をしており、実際の計画支出と一致するよりも多くの国民所得を生み出してきた。

このような状況では、計画外の在庫の増加は、企業が彼らの期待に誤っているという合図を提供します。 企業は、生産量と国民所得を減少させることによって、この予定外の在庫の増加に対処することになります。

在庫調整サイクルは、数量調整会社が彼らの期待と生産の決定を計画された支出に合わせるために行う周期的調整の重要な部分です。

在庫サイクルの重要性は、それらが生産と所得の変化をもたらし、それが経済を均衡状態に戻すことです。 増産するという決定は、より多くの雇用が創出され、より高い国民所得が計画的支出の増加をもたらすことを意味します。

企業は、予想される支出と予想される金額が一致し、それ以上予定外の在庫の減少がなくなるまで、生産高、収入、雇用を増加させ続けるでしょう。 Y * -E *の組み合わせ、つまり、集約需要関数によって集約供給ラインが45 0になると、平衡に達します。

同様に、企業は、予定外の在庫の増加がなくなるまで、生産高、所得、雇用を減少させ続けるでしょう。 もう一度、所得調整は経済をY * -E *の組み合わせに戻します。 その時点で、計画在庫が保持されており、企業は計画支出とちょうど同じくらいの金額を生産しています。

支出の乗数

理解することが重要であるこの収入調整メカニズムの追加機能があります。 総需要関数（式8.14）では、計画総支出が2つの要素で構成されていることがわかります。（a）自律支出要素（A = C 0 + I + G + X）。 （b）国民所得の水準によって引き起こされる支出[c（1 - t） - m] Y。

自律的支出の要素の1つが変化した場合、実質GDP（および国民所得）にどのような影響がありますか。 計画支出が増加すれば実質GDPと国民所得は増加し、計画支出が減少すれば減少することを私たちは知っています。 現在の関心事は、自律的支出の変化によって引き起こされる計画支出の変化（例えば、政府支出の増加）の後に、実質GDPと国民所得がどれだけ変わるかということです。

経済学者たちは支出乗数の概念を発展させて、自治支出の所与の変化に対して国民所得（Y）がどれだけ変化するかを推定する（A）。

図8.9は支出倍率のプロセスを示しています。 当初の均衡状態から、自律的支出の変化は総需要を瞬時に後押しします。 企業は、前のセクションで説明したように増加した計画支出に対応し、増加した実質GDPを生み出すために雇用を増加させます。 賃金と他の投入物への支払いが増えると、それは国民所得の増加につながります。

国民所得の増加はさらなる消費支出を引き起こし、それが総需要の増加につながる。 国民所得の増加の一部は、納税の増加、輸入の増加、貯蓄の増加という形で漏洩します。

このプロセスは、誘発された支出が非常に小さくなり、実質GDPがそれ以上増加しなくなるまで続きます。 このプロセスは、自律的支出の減少とは逆に作用します。

支出乗数の公式表現は、均衡国民所得と支出の関係から直接導き出されます。

総需要関数はE = A + [c（1 - t） - m] Yとして与えられた。 国民所得均衡条件は次のように与えられる。

（8.15）Y = E

均衡条件を総需要関数（8.14）に代入すると、次のようになります。

（8.16a）Y = E = A + [c（1 - t） - m] Y

そして、Yについて解く（左側にYの項を集める）と、

（8.16b）Y [1 - c（1 - t）+ m] = A

したがって、均衡所得は次のとおりです。

（8.16）Y = 1 / [1 - c（1 - t）+ m] A

支出乗数（α）は、式（８．１６）のＡ項の隣の係数である。

（８．１７）α＝ ΔＥ ／ ΔＹ ＝ １ ／ ［１ − ｃ（１ − ｔ）＋ ｍ］

したがって、Aが$ 1変化すると、Yは1 / [1 - c（1 - t）+ m]またはαのA倍の変化で変化します。

支出の乗数を定義する用語を調べると、それは消費の限界傾向（c）、限界税率（t）、および限界輸入傾向を含む比率であることがわかります。

第4章で学んだツールを適用すると、次のことがわかります。

• 他のものが同じであれば、消費する限界傾向が高いほど、支出倍率が高くなります。
• 他のものが等しい、税率が低いほど支出倍率が高くなります。
• 他のものが同じ、輸入の限界傾向が低いほど、支出の乗数は高いです。
• 反対に、cが小さく、tとmが大きい場合も同様です。

ここでの課題は、これらの結論につながる経済的プロセスを説明することです。

私たちは、総需要が（生産的投入への支払いを通じて）所得を生み出すことで生産を促進するという本質的な洞察から始めます。 したがって、使われたものはその期間に収入を生み出し、その収入はその後利用可能になります。 たとえば、財やサービスを生産するために企業に雇われている労働者は、生産プロセスへの原材料やその他の投入物の供給者と同様に、彼らが稼いだ収入を使います。

出力生産から生じる支払いから得られる収入を使用することができる様々な方法があります。 収入は以下の用途に使用できます。

• 消費量の増加
• 節約が増えました。
• 政府に対する納税義務を放棄する。
• 輸入支出の増加

結論

今週は乗数と均衡所得の変化を分析してこの章を終えます。

サタデークイズ

サタデークイズは明日また戻ってきます。