#25 Abba Lerner ～Investment and interest rates bill 2019/8/10
https://nam-students.blogspot.com/2019/06/investment-and-interest-rates-bill.html@
ミッチェル#25:407に対応?
Investment and interest rates – Bill Mitchell – Modern Monetary Theory
2012/8/10
http://www2.kumagaku.ac.jp/teacher/~sasayama.../macroecon/lecture10.html
投資の限界効率表
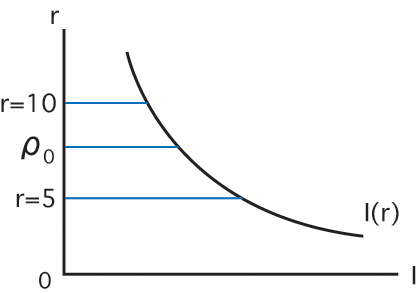
市場利子率が10%ならば，ρoの限界効率の投資は採用
されませんが，利子率が5%ならば，この投資プロジェクト
は採用されます．従って，利子率が低下するほど投資は
増大することがわかります．利子率が上昇すれば，より
高い限界効率の投資しか実行されません．逆に，利子率
が低下すれば低い限界効率の投資でも実行することができます．
すなわち，「投資は利子率の減少関数である」ということ
が明らかになりました．これがケインズによる投資の
限界効率の考え方です．
Consider Figure 12.10 which shows three investment projects A, B and C that a firm has available to it ranked by their respective MEC. Project A has an IRR (or MEC) of 10 per cent, while Project B has an MEC of 8 per cent and Project C has an IRR of 5 per cent.
Figure 12.10 MEC and Investment Projects
#25:406の図に対応
Investment and interest rates
I am now using Friday’s blog space to provide draft versions of the Modern Monetary Theory textbook that I am writing with my colleague and friend Randy Wray. We expect to complete the text by the end of this year. Comments are always welcome. Remember this is a textbook aimed at undergraduate students and so the writing will be different from my usual blog free-for-all. Note also that the text I post is just the work I am doing by way of the first draft so the material posted will not represent the complete text. Further it will change once the two of us have edited it.
Introduction to Cash Flow Discounting and Present Value
Investment and production decisions taken by firms are influenced by the expectations that entrepreneurs form about future revenue and cost streams which allow them to make guesses about what their profits might be.
Firms will try to formulate these expectations into specific cash flows and outlays across the time horizons that are appplicabe to the particular investment good. Different investment options will typically have different revenue and cost outlay profiles over time. So one piece of equipment might involve higher outlays in the more near future but deliver higher returns in a later period compared to another piece of equipment that delivers the same flow of production services but is cheaper in the near future but
In this section we introduce some introductory concepts to allow us to compare flows of funds between different periods in the future. The reason that this is not a straightforward exercise of su
Start with a rate of interest (the cost of obtaining funds) of 10 per cent. If you had $100 now and loaned it for a year then at the end of year 1 you would have $100 plus the interest earned which is given by the following formula:
(12.17) $100 + 0.10 x $100 = $100(1 + 0.10) = $110
This simple arithmetic generalises to the following model of compound interest:
(12.18) Pt+1 = Pt(1 + i)
where Pt+1 is the amount received in period t + 1 where t is now, Pt is the amount you invest now, and i is the nominal rate of interest.
What if you were to reinvest Pt+1 for the second year? You would expect to receive an amount Pt+2 according to the following formula:
(12.19) Pt+2 = Pt+1(1 + i)
From Equation (12.18) we know that Pt+1 = Pt(1 + i) so Equation (12.19) can be re-written as:
(12.20) Pt+2 = Pt(1 + i)(1 + i) = Pt(1 + i)2
We can generalise this if the period of the loan is n years to:
(12.21) Pt+n = Pt(1 + i)n
Equation (12.21) is a compound interest formula and assumes that the interest is added (compounded) at the end of each year. The formula gets more complicated if there are multiple compounding periods within the year. We do not consider these complications in this textbook.
You will appreciate from the concept of compound interest that a sum invested at a positive interest now will grow to a larger future nominal amount in the future. We can deploy this concept in reverse to calculate what a sum of cash that you expect to receive at some future date is worth today. You can see that this type of information is an essential component for a firm making investment decisions where the cash returns and outlays are received or incurred at some future date.
In general terms, how much would you have in today’s dollars if you knew you were to receive Pt+1 (that is, a sum of cash Pt+1 next year)?
From Equation (12.18) we can see that:
(12.22) Pt = Pt+1/(1 + i)
Consider our initial example where Pt+1 was $110 and i was 10 per cent. Equation (12.22) tells us that $110 received at the end of the year would be worth $100 now if the interest rate over the year was 10 per cent.
In this way, a firm can convert all future cash flows into current value using a generalised form of Equation (12.22).
You can think about this in this way. If you needed cash now and knew you were going to receive $110 at the end of this year and the current interest rate was 10 per cent then how much would you be able to sell your future claim on income for in the open market? The answer is $100 as long as the receipt at the end of the year was risk free and the inflation rate was zero (complications we will consider in a later Chapter).
No-one would be prepared to give you say $105 now in return for $110 at the end of the year if the interest rate was 10 per cent because they would be losing money. Similarly, you would be flooded with offers below $100 now if you were selling an asset (income flow) that would deliver the buyer $110 and interest rates were 10 per cent.
We also know that the current value of a future cash flow will be sensitive to the rate of interest. Imagine that the rate of interest was to fall during the year to 5 per cent. Then the future flow of cash of $110 would be worth $104.76 (110/(1+0.05)). You can verify that if you were to loan $104.76 now at 5 per cent then at the end of year 1 you would have $110. The future cash flow is less valuable now if the interest rate was to rise.
The current value of a future cash flow is called its present value (PV). The general formula for present value of a cash flow to be received at the end of period n is:
(12.22) Pt = Pt+n/(1 + i)n
What about the situation where the expected cash flows of varying are distributed across several different time periods? In that case, the present value of a flow at time t, Pt can be written as:
(12.23) Pt = Pt+1/(1 + i) + Pt+2/(1 + i)2 + Pt+3/(1 + i)3 + … + Pt+n/(1 + i)n
where the … refers to terms we have not written between time period t + 3 and n.
The conversion of disparate future cash flows across time into present values is generally called Discounted Cash Flow analysis.
Investment and the rate of interest
We are now in a position to consider the impact of the rate of interest on investment expenditure in more detail. As we learned in Chapters 7 and 8, investment decisions taken by entrepreneurs form an important component of total aggregate demand and income and as a result help explain changes in total employment.
Firms are continually making guesses about the future in terms of what the overall state of demand for their products will be, what they are likely to receive by way of revenue if their sales match these expectations, and what it will cost them to produce the output necessary to meet this demand.
Firms also have various choices about what products to produce and how they can produce them (for example, choice of technique). Firms are driven by the desire to make profit and will thus make choices among different types of productive equipment on the basis of which will contribute the most profit subject to a range of other considerations, many of which are subjective. For example, a firm that wishes to keep good standing in the community will probably eschew the use of equipment that is damaging to the local environment even if the use was legal and generated more profits than other options.
Whether firms use retained profits to fund future investment or seek funds from the markets there is a cost involved in purchasing new capital. A firm may have retained earnings to invest. It has the choice of investing them in new plant and equipment, or perhaps, purchasing financial assets which yield a positive rate of return (for example, a bond). While the firm will be driven by the need to stay in its present business and therefore defend its market share, which means it will usually want to use the funds available to it to purchase best practice, productive infrastructure; it may, at times, hold off from upgrading its productive capital if the circumstances are not conducive.
Investment decisions will thus depend on whether the productive asset being purchased delivers a positive return above the cost.
We can build on our understanding of present value (PV) to advance this idea in relation to the investment in productive capital.
Keynes and the Marginal Efficiency of Investment
In Chapter 11 The Marginal Efficiency of Capital of the The General Theory of Employment Interest and Money (published in 1936) John Maynard Keynes developed his theory of investment based in his concept of the Marginal Efficiency of Capital.
Keynes defined the Marginal Efficiency of Capital as:
… being equal to that rate of discount which would make the present value of the series of annuities given by the returns expected from the capital-asset during its life just equal to its supply price. This gives us the marginal efficiencies of particular types of capital-assets. The greatest of these marginal efficiencies can then be regarded as the marginal efficiency of capital in general.
His definition is difficult to understand and created some controversy, which we will touch upon here.
It is clear that he was thinking about two aspects of the investment decision: (a) the “prospective yield of the investment” which is a “series of annuities Q1, Q2, … Qn”. These are future flows of cash associated with an investment which the entrepreneur “expects to obtain from selling its output”. You can relate these flows to the earlier discussion of compound interest; and (b) the supply-price of the asset which he said was the “the price which would just induce a manufacturer newly to produce an additional unit of such assets” or in more simple language – “the replacement cost”.
The rate of discount he was referring to is also known as the internal rate of return of an project. As we saw in the last section, we can calculate a present value for any future cash flow stream. A net present value would be the present value of the revenue to be received minus the present value of the costs of the project.
A positive net present value coincides with a project that earns a positive rate of return in current dollars where a negative present value means that the project would lose money in current dollars.
The internal rate of return is the interest rate that would discount future income and cost outlays such that the net present value was zero.
Consider Figure 12.9 which provides data for a specific investment project. In the current year, the firm has to spent $10,000 to purchase the equipment. In subsequent years it receives the cash flows as indicated. We can assume there is no scrap value for the equipment after Year 5.
Figure 12.9 A Simple Cash Flow for an Investment Project
What is the internal rate of return (IRR) for this project?
The present value of the costs are $10,000 because they are all incurred in the current year (that is, now). The dollar sum of the cash returns is $15,000 but as we saw in the previous section, the dollar amounts cannot be compared across time periods because of the impacts of compounding.
The present value of the flow of revenue is given by the formula in Equation (12.23). Using the data in Figure 12.9 we would write this equation as:
(12.24) PV = $2,500/(1 + i) + $3,200/(1 + i)2 + $3,500/(1 + i)3 + $3,300/(1 + i)4 + $2,400//(1 + i)5
The internal rate of return is the discount rate (i)) that satisfies the following equation:
(12.25) NPV = -$10,000 + $2,500/(1 + i) + $3,200/(1 + i)2 + $3,500/(1 + i)3 + $3,300/(1 + i)4 + $2,400//(1 + i)5 = 0
The solution for i requires mathematics that are beyond the reach of this textbook (for interested students we have to solve the roots of Equation 12.25). You can use spreadsheet functions to do the task for you if you input the relevant data.
In our case, the IRR is 15.1 per cent.
You might like to input the data into a spreadsheet and compute the present value in Equation (12.24) using a discount rate of 15.1 per cent. You should verify that it equal to $10,000, which is exactly the present value of the initial outlay. The actual result you get may not equal $10,000 but this is due the approximate iterative solutions used by the spreadsheet.
This project will be profitable if the cost of borrowing funds to fund the project (that is, the market rate of interest) is below the IRR.
We can interpret Keynes’ concept of the MEC as being the return at the marginthat a firm would expect to earn by investing in new capital equipment. That is, it is not the market return on existing assets.
Consider Figure 12.10 which shows three investment projects A, B and C that a firm has available to it ranked by their respective MEC. Project A has an IRR (or MEC) of 10 per cent, while Project B has an MEC of 8 per cent and Project C has an IRR of 5 per cent.
Figure 12.10 MEC and Investment Projects
The firm must consider how much new capital expenditure it will incur for the coming year. If the market rate of interest is currently 9 per cent, then the firm would only be interested in investing in Project A, which means that its capital expenditure in the current planning period will be limited to Project A.
Should the market interest rate drop to below 8 per cent, then it will be profitable to borrow sufficient funds (or use retained earnings) and invest in both Project A and Project B. As a consequence total investment will rise. The firm will expand investment to Project C if the market rate of interest drops below 5 per cent.
The downward sloping MEC line that is depicted in Figure 12.10 summarises the investment response of the firm to changes in the market interest rate.
As a result a simple investment model of investment emerges whereby total investment in the economy is considered to be a downward function of the market rate of interest as in the Equation (12.25):
(12.25) I = I0 – bi
会社は、来年度にどれだけの新たな設備投資が必要になるかを検討しなければなりません。市場金利が現在9％の場合、会社はプロジェクトAへの投資にのみ関心があります。つまり、現在の計画期間中の設備投資はプロジェクトAに限定されます。
市場金利が8％を下回ると、十分な資金を借りて（または利益剰余金を使用して）プロジェクトAとプロジェクトBの両方に投資するのが有益になります。その結果、総投資額は増加します。市場金利が5％を下回ると、同社はプロジェクトCへの投資を拡大する。
図12.10に示されている下降勾配のMECラインは、市場金利の変化に対する会社の投資反応を要約しています。
結果として、投資の単純な投資モデルが出現し、それによって経済への総投資は式（12.25）のように市場金利の下方関数であると考えられる。
（12.25）I = I0 - bi
where I is total investment, I0 is some level of investment that is independent of the market rate of interest and b is the sensitivity of investment to the market rate of interest, i.
When considering Equation (12.25) you should always consider what lies behind it in terms of the MEC. The simple investment model, which says that rising market rates of interest lead to lower total investment is based on an assumption that all other things are equal. But as we have seen, underpinning the concept of the MEC is a comparison between the demand-side (expected revenue) and the supply-side (the replacement cost).
In a growing economy, it is likely that aggregate demand conditions will improve at times when the market rate of interest rises. The former will improve the revenue cash flows over time and increase the MEC for each project. In other words, we would not observe investment falling when the market rate of interest rose because the IRR of each project could also be increasing.
Thus it is important to avoid applying a mechanical interpretation of the concept of the MEC. Keynes, in fact, did not think investment would be very responsive to changes in the market rate of interest, especially when the economy was in recession or boom. Expectations formed by entrepreneurs underpinned their MEC calculations.
ここで、Iは総投資額、I 0は市場金利とは無関係のある水準の投資、bは市場金利に対する投資の感応度です。
式（12.25）を検討する際には、MECの観点からその背後にあるものを常に考慮する必要があります。市場金利の上昇が総投資の減少につながるという単純な投資モデルは、他のすべてのものが等しいという仮定に基づいています。しかし、これまで見てきたように、MECの概念を支えるのは、需要側（予想収益）と供給側（交換コスト）の比較です。
成長経済では、市場金利が上昇するときに総需要条件が改善する可能性があります。前者は、経時的に収益のキャッシュフローを改善し、各プロジェクトのMECを増加させるでしょう。つまり、各プロジェクトのIRRも増加している可能性があるため、市場金利が上昇したときに投資が減少することはありません。
したがって、MECの概念の機械的解釈を適用しないようにすることが重要です。ケインズは、事実、投資が市場金利の変化に非常に敏感に反応するとは考えていませんでした、特に経済が不況またはブームにあったとき。起業家によって形成された期待は彼らのMEC計算を支えた。
When the economy was in recession, entrepreneurs would become pessimistic and this would negatively impact on their assessment of the future returns from different projects. Further, with substantial excess productive capacity firms are unlikely to expand the capital stock even if new investment projects become cheaper as the central bank cuts the market interest rate to stimulate demand.
The extreme optimism that typically accompanies a boom also would reduce the sensitivity of investment to changes in the market rate of interest. With expected returns high, firms will be prepared to pay higher borrowing costs.
We could express this enhanced optimism by a shift outwards in the MEC line in Figure 12.10 which would make more Projects worth pursuing at a given market rate of interest.
If entrepreneurs became excessively pessimistic then the MEC line would shift inwards and fewer projects would be deemed profitable at a given market rate of interest even if the technical aspects of the equipment was unchanged.
For Keynes then, investment was a very subjective act and responsive to how firms felt about the economy. Even though Equation (12.25) seems simple the ideas underpinning it were anything but.
We consider the crucial role of expectations and what factors firms might consider when forming expectations of future returns in Chapter 17 Keynes and Classics and modern variants.
The concept of the MEC was refined by later economists including Abba Lerner who preferred the term Marginal Efficiency of Investment (MEI).
There were many criticisms of this approach to investment theory
経済が不況に陥ったとき、起業家は悲観的になり、これは異なるプロジェクトからの将来の収益の彼らの評価に悪影響を及ぼすでしょう。さらに、生産能力が大幅に過剰であるため、中央銀行が需要を刺激するために市場金利を引き下げて新規投資プロジェクトがより安くなったとしても、企業は資本ストックを拡大する可能性は低い。
通常ブームを伴う極端な楽観主義はまた、市場金利の変動に対する投資の敏感さを減少させるでしょう。期待収益率が高い場合、企業はより高い借入コストを支払う用意があるでしょう。
図12.10のMECラインで外向きにシフトすることで、このように楽観的な見方を強めることができます。これにより、特定の市場金利で追求する価値のあるプロジェクトが増えます。
起業家が過度に悲観的になると、MECラインは内側にシフトし、たとえ機器の技術的側面が変わらなくても、与えられた市場金利で収益性があるとみなされるプロジェクトは少なくなります。
ケインズにとって当時、投資は非常に主観的な行動であり、企業が経済についてどう感じたかに対応していました。式（12.25）は単純に思えますが、それを支える考えは他にはありませんでした。
第17章ケインズとクラシックおよび現代の変種で、期待の決定的な役割、および将来のリターンに対する期待を形成する際に企業が考慮する要因について検討します。
MECの概念は、投資の限界効率（MEI）を好むAbba Lernerを含む後の経済学者によって洗練されました。
投資理論へのこのアプローチに対する多くの批判がありました
A substantial criticism focused on the logic of a downward sloping MEC line at times when involuntary unemployment was observed. If we consider the expenditure multiplier, then aggregate demand rises by some multiple of a rise in investment expenditure and output rises.
If the MEC is influenced by expected future returns then the increased national income arising from the increased investment would logically lead to higher expected future revenue. In that case, the MEI will shift outwards as not above which means that investment should increase as a result. This would then stimulate further multiplied increases in aggregate demand and output and so the process would continue.
With plenty of excess capacity in the form of high unemployment, it is easy to conceive of a situation where investment would be indeterminate as the multiplied income increases feedback into further investment as expected returns improve. As a consequence, the firms will progressively invest in an increasing number of projects and the market interest rate would lose all relevance.
Once again we see the importance of expectations in this approach to investment.
The response to this criticism was also varied.
One approach attacked the idea that the MEI line could be aggregated across all firms to become the aggregate (or macro) investment function. It was argued that this “aggregate” investment line would over-estimate the investment that would accompany a fall in interest rates. The argument noted that if the interest rate was to fall and borrowing costs for all firms were now lower, then as all firms expanded investment in productive capacity, the rising demand for capital goods would drive their price up which would reduce the MEC lines for all firms.
Some economists have attempted to distinguish the MEC from the MEI along these lines, saying that the MEI is the relationship between total investment and market interest rates when the demand effects on the price of capital goods is taken into account.
Michel Kalecki introduced what he termed the Principle of Increasing Risk which brought together the investment decision and the risk of increased indebtedness that firms would carry as they expanded investment. As firms extended their exposure the success of the marginal projects in terms of generating realised returns became more crucial. Kalecki argued that firms would become increasingly risk averse as their debt levels rose and this would be expressed by more sobre expectations of the future returns from various projects.
Kalecki thus considered that increasing risk would thus ensure that the MEI was downward sloping with respect to the market rate of interest.
[NOTE: MORE TO COME ON THIS]不本意な失業が見られたときには、かなり下落したMECラインの論理にかなりの批判が集中した。支出の乗数を考慮すると、総需要は投資支出の増加の何倍かで増加し、生産量が増加します。
MECが予想される将来の収益に影響されるのであれば、投資の増加から生じる国民所得の増加は論理的に予想される将来の収益の増加につながるでしょう。その場合、MEIは上記の範囲を超えて外側にシフトすることになり、結果として投資は増加するはずです。これはその後、総需要と生産高のさらなる増加した増加を刺激することになるので、プロセスは継続するだろう。
高い失業率という形で十分な余剰能力があるため、期待収益が改善するにつれて、増やされた収入がさらなる投資へのフィードバックを増加させるため、投資が不確定となる状況を想像するのは簡単です。結果として、企業はますます多くのプロジェクトに徐々に投資し、市場金利はすべての関連性を失うことになります。
この投資アプローチへの期待の重要性が再びわかります。
この批判に対する反応もさまざまでした。
あるアプローチでは、MEIラインをすべての企業に集約して集約（またはマクロ）投資機能にすることができるという考えが攻撃されました。この「総計」投資ラインは金利の低下に伴う投資を過大評価するであろうと主張された。議論は、金利が下落し、すべての企業の借入コストが低下した場合、すべての企業が生産能力への投資を拡大するにつれて、資本財に対する需要の高まりが価格上昇を招き、すべての企業のMECラインを引き下げることになる企業です。
MEIは資本財の価格への需要の影響を考慮に入れたときの総投資と市場金利との関係であると言って、経済学者の中にはこれらの線に沿ってMECをMEIと区別しようと試みた人もいる。
Michel Kalecki氏は、投資の決定と、投資拡大に伴って企業が負う債務の増加のリスクをまとめた「リスク増加の原則」と名付けたものを紹介しました。企業がエクスポージャーを拡大するにつれて、実現収益を生み出すという点で限界プロジェクトの成功がより重要になりました。 Kalecki氏は、債務水準が上がるにつれて企業はリスク回避をますます強めることになり、これはさまざまなプロジェクトからの将来の収益に対する予想以上に厳しい予想によって表されるだろうと主張した。
したがって、Kalecki氏は、リスクの増大によって、MEIが市場金利に対して下方に傾斜していることを保証すると考えました。
[注：これ以上来ない]
Alternative Olympic Games Medal Tally
My Alternative Olympic Games Medal Tally is now active.
I update it early in the day and again around lunchtime when all the sports are concluded for the day.
Saturday Quiz
The Saturday Quiz will be back again tomorrow. It will be of an appropriate order of difficulty (-:
That is enough for today!
(c) Copyright 2012 Bill Mitchell. All Rights Reserved.
投資と金利
billFriday、2012年8月10日
私は今、金曜日のブログスペースを使って、同僚や友人のRandy Wrayと書いている現代通貨理論の教科書のドラフト版を提供しています。私たちは今年の終わりまでにこのテキストを完成させる予定です。コメントはいつでも大歓迎です。これは学部生を対象とした教科書なので、執筆は私のいつものブログとは違ったものになるでしょう。また、私が投稿したテキストは最初のドラフトとして私が行っている作業であり、投稿された資料は完全なテキストを表すものではありません。さらに私たち二人がそれを編集したらそれは変わります。
キャッシュフロー割引の概要と現在価値
企業による投資と生産の決定は、起業家が将来の収益とコストの流れについて形成する期待に影響され、それによって彼らは自分たちの利益がどうなるかについて推測することができます。
企業はこれらの期待を具体的なキャッシュフローと特定の投資財に当てはまる期間にわたる支出に定式化しようとします。投資オプションが異なれば、通常、経時的な収益およびコスト支出のプロファイルも異なります。そのため、1つの機器で近い将来にはより高い費用がかかりますが、生産サービスの流れは同じであるが近い将来にはより安価である別の機器と比較して、より遅い期間でより高い収益が得られます。
このセクションでは、将来の異なる期間における資金の流れを比較できるようにするために、いくつかの導入概念を紹介します。これがsuの直接的な練習ではない理由
10パーセントの利子率（資金を得るためのコスト）から始めましょう。あなたが今100ドルを持っていて1年の間それを貸したならば、1年目の終わりにあなたは次の公式によって与えられる100ドルプラス得られた金利を持つでしょう。
（12.17）$ 100 + 0.10 x $ 100 = $ 100（1 + 0.10）= $ 110
この単純な算術は、以下の複利のモデルに一般化されます。
（12.18）Pt + 1 = Pt（1 + i）
ここで、Pt + 1はtが現在の期間t + 1に受け取った金額であり、Ptは現在投資している金額であり、iは名目金利です。
2年目にPt + 1を再投資する場合はどうなりますか？次の式に従って、Pt + 2の金額を受け取ることになります。
（12.19）Pt + 2 = Pt + 1（1 + i）
式（１２．１８）から、Ｐｔ ＋ １ ＝ Ｐｔ（１ ＋ ｉ）であることが分かるので、式（１２．１９）は以下のように書き直すことができる。
（12.20）Pt + 2 = Pt（1 + i）（1 + i）= Pt（1 + i）2
ローンの期間がn年の場合、これを一般化できます。
（12.21）Pt + n = Pt（1 + i）n
式（12.21）は複利計算式であり、利子は各年末に加算（合成）されると仮定しています。年内に複数の複利計算期がある場合、式はより複雑になります。この教科書ではこれらの複雑さを考慮していません。
複合利子の概念から、正の利子で投資された金額は将来的に将来の名目元本金額まで増加することがわかります。この概念を逆に展開して、将来のある日に受け取ると予想される現金の総額が今日価値がある額を計算できます。あなたは、この種の情報が、将来のある日に現金収益と支出が受領または発生する場合に投資決定を下す企業にとって不可欠な要素であることがわかります。
一般的に言えば、Pt + 1（つまり、来年のPt + 1の現金の合計）を受け取ることがわかっていたら、今日のドルでいくらになりますか。
式（12.18）から、次のことがわかります。
（12.22）Pt = Pt + 1 /（1 + i）
Pt + 1が110ドル、iが10パーセントの最初の例を考えてみましょう。式（12.22）は、その年の利子率が10％であれば、年末に受け取った$ 110が今$ 100になることを示しています。
このようにして、会社は方程式（12.22）の一般形を使用して将来のすべてのキャッシュフローを現在価値に変換することができます。
あなたはこのようにこれについて考えることができます。あなたが今現金を必要としていて、あなたが今年の終わりに110ドルを受け取ることになっていて、現在の金利が10パーセントであることを知っていたなら、あなたはオープンマーケットで収入の将来の請求を売ることができるでしょうか？年末の領収書にリスクがなく、インフレ率がゼロである限り、答えは100ドルです（後の章で検討する複雑な問題）。
利子率が10％の場合、年末には110ドルと引き換えに105ドルと言ってもいいでしょう。同様に、買い手に110ドルを提供する資産（収入の流れ）を売っていて金利が10％だった場合、100ドル以下のオファーが殺到することになります。
また、将来のキャッシュフローの現在価値が金利に敏感になることもわかっています。利子率がその年の間に5パーセントに落ちることになっていたと想像してください。それから110ドルの将来の現金の流れは104.76ドル（110 /（1 + 0.05））の価値があるでしょう。あなたは今5パーセントで104.76ドルをローンするつもりならばそれからyの終わりにそれを確かめることができます
耳1あなたは110ドルを持っているでしょう。金利が上昇した場合、将来のキャッシュフローは今ではあまり価値がありません。
将来のキャッシュフローの現在価値は、現在価値（PV）と呼ばれます。期間nの終わりに受け取るキャッシュフローの現在価値の一般式は、次のとおりです。
（１２．２２）Ｐｔ ＝ Ｐｔ ＋ ｎ ／（１ ＋ ｉ）ｎ
予想キャッシュフローの変動が複数の異なる期間にわたって分散している状況についてはどうですか。その場合、時間tにおけるフローの現在値Ptは次のように書くことができます。
（12.23）Pt = Pt + 1 /（1 + i）+ Pt + 2 /（1 + i）2 + Pt + 3 /（1 + i）3 +…+ Pt + n /（1 + i）n
ここで…は、期間t + 3とnの間に書いていない用語を指します。
経時的に異なる将来キャッシュフローを現在価値に変換することは、通常、割引キャッシュフロー分析と呼ばれます。
投資と金利
我々は現在、投資支出に対する金利の影響をより詳細に検討する立場にある。第7章と第8章で学んだように、起業家による投資決定は総需要と総収入の重要な要素を形成し、結果として総雇用の変化を説明するのに役立ちます。
企業は、自社の製品に対する全体的な需要の状態がどのようになるのか、売上がこれらの期待に一致する場合に収益として受け取る可能性があるのか、および生産のためにかかるコストの観点から、将来について継続的に推測しています。この需要を満たすために必要です。
企業はまた、どの製品を生産するのか、そしてどのようにしてそれらを生産することができるのかについて様々な選択をする（例えば、技術の選択）。企業は利益を上げたいという願望に動かされており、したがって、さまざまな種類の生産設備の中から選択することになります。例えば、地域社会で優位を保ちたい企業は、たとえその使用が合法的で他の選択肢よりも多くの利益を生み出したとしても、おそらく地元の環境に害を及ぼす機器の使用を避けるでしょう。
企業が将来の投資に資金を供給するために利益剰余金を使用するか、市場から資金を調達するかにかかわらず、新しい資本の購入にはコストがかかります。会社は投資する利益を留保しているかもしれません。それはそれらを新しい工場や設備に投資するか、あるいはおそらく正の収益率をもたらす金融資産（例えば債券）を購入するかの選択をする。同社は現在の事業を維持し、市場シェアを守る必要性によって動かされますが、それは通常、ベストプラクティスの生産的なインフラストラクチャを購入するために利用可能な資金を使用したいことを意味します。状況が助長されていない場合、それは時々、その生産的資本をアップグレードするのを遅らせるかもしれません。
したがって、投資の決定は、購入される生産的資産がコストを上回るプラスの収益をもたらすかどうかによって異なります。
生産的資本への投資に関連してこの考えを進めるために、私たちは現在価値（PV）についての私たちの理解の上に構築することができます。
ケインズと投資の限界効率
第11章では、「雇用の利子と貨幣の一般理論の資本の限界効率」（1936年発行）で、ジョン・メイナード・ケインズは、資本の限界効率の概念に基づいて投資理論を開発しました。
ケインズは、限界資本効率を次のように定義した。
…その生涯の間に資本資産から期待される収益によって与えられる一連の年金の現在価値をちょうどその供給価格に等しくするであろう割引率に等しい。これにより、特定の種類の資本資産の限界効率性が得られます。これらの限界効率のうち最大のものは、一般的に資本の限界効率と見なすことができます。
彼の定義は理解するのが難しく、ここで触れようとするいくつかの論争を引き起こしました。
彼が投資決定の2つの側面について考えていたのは明らかです。（a）「一連の年金Q1、Q2、…Qn」である「予想投資利回り」。これらは、起業家が「アウトプットの売却から得ることを期待している」投資に関連する将来のキャッシュフローです。あなたはこれらの流れを複利の以前の議論に関連づけることができます。 （b）彼が言った資産の供給価格は、「製造業者にそのような資産の追加単位を新たに生産させるだけの価格」またはより単純な言葉でいうと「交換費用」であった。
彼が言及していた割引率は、プロジェクトの内部収益率としても知られています。前のセクションで見たように、将来のキャッシュフローの流れの現在価値を計算することができます。正味現在価値は、受け取る収入の現在価値からプロジェクトのコストの現在価値を引いたものです。
正味現在価値は、現在のドルで正の収益率を得るプロジェクトと一致します。負の現在価値は、プロジェクトが現在のドルでお金を失うことを意味します。
内部収益率は、正味現在価値がゼロになるように将来の収入と費用の支出を割り引く金利です。
特定の投資プロジェクトのデータを提供する図12.9を検討してください。今年、同社は機器の購入に1万ドルを費やさなければならなかった。その後の年に、それは示されるようにキャッシュフローを受け取る。 5年目以降は、設備に不良値がないと見なすことができます。
図12.9投資プロジェクトの単純なキャッシュフロー
このプロジェクトの内部収益率（IRR）はいくらですか。
コストの現在価値は10,000ドルです。これは、それらがすべて今年度（つまり現在）に発生したためです。現金収益のドル合計は15,000ドルですが、前のセクションで見たように、複利の影響のために期間をまたがってドル金額を比較することはできません。
収入の流れの現在価値は、式（12.23）の式で与えられます。図12.9のデータを使用して、この式を次のように書きます。
（12.24）PV = $ 2,500 /（1 + i）+ $ 3,200 /（1 + i）2 + $ 3,500 /（1 + i）3 + $ 3,300 /（1 + i）4 + $ 2,400 //（1 + i）5
内部収益率は、次の式を満たす割引率（i）です。
（12.25）NPV = - $ 10,000 + $ 2,500 /（1 + i）+ $ 3,200 /（1 + i）2 + $ 3,500 /（1 + i）3 + $ 3,300 /（1 + i）4 + $ 2,400 //（1 + i） 5 = 0
iの解法は、この教科書の範囲を超えた数学を必要とします（興味がある学生のために、式12.25の根を解かなければなりません）。関連データを入力した場合は、スプレッドシート機能を使用してタスクを実行できます。
私たちの場合、IRRは15.1％です。
スプレッドシートにデータを入力し、15.1パーセントの割引率を使用して式（12.24）で現在の値を計算します。あなたはそれが正確に最初の支出の現在価値である$ 10,000に等しいことを確かめるべきです。実際の結果は1万ドルにはならないかもしれませんが、これはスプレッドシートで使用されている概算の反復解法によるものです。
このプロジェクトは、プロジェクトに資金を提供するための資金を借りるためのコスト（つまり、市場金利）がIRRを下回る場合には有益となります。
ケインズのMECの概念は、企業が新しい資本設備に投資することによって稼ぐことを期待する限界のリターンであると解釈することができます。つまり、既存資産の市場収益ではありません。
企業が利用可能な3つの投資プロジェクトA、B、CをそれぞれのMECでランク付けした図12.10を検討してください。プロジェクトAのIRR（またはMEC）は10％、プロジェクトBのMECは8％、プロジェクトCのIRRは5％です。
図12.10 MECと投資プロジェクト
Figure 12.10 MEC and Investment Projects
会社は、来年度にどれだけの新たな設備投資が必要になるかを検討しなければなりません。市場金利が現在9％の場合、会社はプロジェクトAへの投資にのみ関心があります。つまり、現在の計画期間中の設備投資はプロジェクトAに限定されます。
市場金利が8％を下回ると、十分な資金を借りて（または利益剰余金を使用して）プロジェクトAとプロジェクトBの両方に投資するのが有益になります。その結果、総投資額は増加します。市場金利が5％を下回ると、同社はプロジェクトCへの投資を拡大する。
図12.10に示されている下降勾配のMECラインは、市場金利の変化に対する会社の投資反応を要約しています。
結果として、投資の単純な投資モデルが出現し、それによって経済への総投資は式（12.25）のように市場金利の下方関数であると考えられる。
（12.25）I = I0 - bi
ここで、Iは総投資額、I 0は市場金利とは無関係のある水準の投資、bは市場金利に対する投資の感応度です。
式（12.25）を検討する際には、MECの観点からその背後にあるものを常に考慮する必要があります。市場金利の上昇が総投資の減少につながるという単純な投資モデルは、他のすべてのものが等しいという仮定に基づいています。しかし、これまで見てきたように、MECの概念を支えるのは、需要側（予想収益）と供給側（交換コスト）の比較です。
成長経済では、市場金利が上昇するときに総需要条件が改善する可能性があります。前者は、経時的に収益のキャッシュフローを改善し、各プロジェクトのMECを増加させるでしょう。つまり、各プロジェクトのIRRも増加している可能性があるため、市場金利が上昇したときに投資が減少することはありません。
したがって、MECの概念の機械的解釈を適用しないようにすることが重要です。ケインズは、事実、投資が市場金利の変化に非常に敏感に反応するとは考えていませんでした、特に経済が不況またはブームにあったとき。起業家によって形成された期待は彼らのMEC計算を支えた。
経済が不況に陥ったとき、起業家は悲観的になり、これは異なるプロジェクトからの将来の収益の彼らの評価に悪影響を及ぼすでしょう。さらに、生産能力が大幅に過剰であるため、中央銀行が需要を刺激するために市場金利を引き下げて新規投資プロジェクトがより安くなったとしても、企業は資本ストックを拡大する可能性は低い。
通常ブームを伴う極端な楽観主義はまた、市場金利の変動に対する投資の敏感さを減少させるでしょう。期待収益率が高い場合、企業はより高い借入コストを支払う用意があるでしょう。
図12.10のMECラインで外向きにシフトすることで、このように楽観的な見方を強めることができます。これにより、特定の市場金利で追求する価値のあるプロジェクトが増えます。
起業家が過度に悲観的になると、MECラインは内側にシフトし、たとえ機器の技術的側面が変わらなくても、与えられた市場金利で収益性があるとみなされるプロジェクトは少なくなります。
ケインズにとって当時、投資は非常に主観的な行動であり、企業が経済についてどう感じたかに対応していました。式（12.25）は単純に思えますが、それを支える考えは他にはありませんでした。
第17章ケインズとクラシックおよび現代の変種で、期待の決定的な役割、および将来のリターンに対する期待を形成する際に企業が考慮する要因について検討します。
MECの概念は、投資の限界効率（MEI）を好むAbba Lernerを含む後の経済学者によって洗練されました。
投資理論へのこのアプローチに対する多くの批判がありました
不本意な失業が見られたときには、かなり下落したMECラインの論理にかなりの批判が集中した。支出の乗数を考慮すると、総需要は投資支出の増加の何倍かで増加し、生産量が増加します。
MECが予想される将来の収益に影響されるのであれば、投資の増加から生じる国民所得の増加は論理的に予想される将来の収益の増加につながるでしょう。その場合、MEIは上記の範囲を超えて外側にシフトすることになり、結果として投資は増加するはずです。これはその後、総需要と生産高のさらなる増加した増加を刺激することになるので、プロセスは継続するだろう。
高い失業率という形で十分な余剰能力があるため、期待収益が改善するにつれて、増やされた収入がさらなる投資へのフィードバックを増加させるため、投資が不確定となる状況を想像するのは簡単です。その結果、企業はますます多くのプロジェクトと市場の関心に徐々に投資するようになるでしょう。
st rateはすべての関連性を失います。
この投資アプローチへの期待の重要性が再びわかります。
この批判に対する反応もさまざまでした。
あるアプローチでは、MEIラインをすべての企業に集約して集約（またはマクロ）投資機能にすることができるという考えが攻撃されました。この「総計」投資ラインは金利の低下に伴う投資を過大評価するであろうと主張された。議論は、金利が下落し、すべての企業の借入コストが低下した場合、すべての企業が生産能力への投資を拡大するにつれて、資本財に対する需要の高まりが価格上昇を招き、すべての企業のMECラインを引き下げることになる企業です。
MEIは資本財の価格への需要の影響を考慮に入れたときの総投資と市場金利との関係であると言って、経済学者の中にはこれらの線に沿ってMECをMEIと区別しようと試みた人もいる。
Michel Kalecki氏は、投資の決定と、投資拡大に伴って企業が負う債務の増加のリスクをまとめた「リスク増加の原則」と名付けたものを紹介しました。企業がエクスポージャーを拡大するにつれて、実現収益を生み出すという点で限界プロジェクトの成功がより重要になりました。 Kalecki氏は、債務水準が上がるにつれて企業はリスク回避をますます強めることになり、これはさまざまなプロジェクトからの将来の収益に対する予想以上に厳しい予想によって表されるだろうと主張した。
したがって、Kalecki氏は、リスクの増大によって、MEIが市場金利に対して下方に傾斜していることを保証すると考えました。
[注：これ以上来ない]
ーーーーーーーーーーーーーーー
0 Comments:
コメントを投稿
<< Home