方程式の解法 = 方程式の答の入れ替えパターン = 代数体の入れ替えパターン
これは本当の大発見だ。
それが、既に200年も前に考えられていたことだなんて、気にする必要はない。
理解とは、第二の発見なのだから。
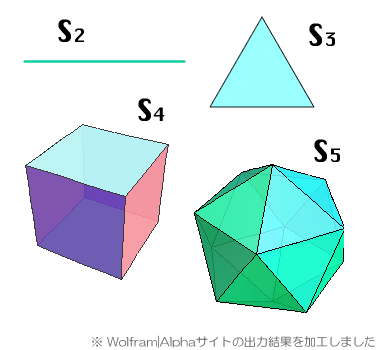 方程式には形があり、群がある。
方程式には形があり、群がある。
二次方程式は、鏡面対称。
2つの答を入れ替える群は、対称群S2
三次方程式は、正三角形。
3つの答を入れ替える群は、対称群S3
四次方程式は、立方体。
4つの答を入れ替える群は、対称群S4
五次方程式は、正二十面体。
5つの答を入れ替える群は、対称群S5
方程式を解く、という操作は、問題をより小さな次数の方程式に還元することだ。
それは、方程式の群を、より小さな部分群に分解するということでもある。
そしてまた、有理数Qから拡大してきた代数体の階段を、一段ずつ降りてゆくことでもある。
方程式、群、体。
この3つは、1つの同じものを、別の側面から見た姿なのだ。
※ ここでは方程式の係数が有理数Qであるとして話を進める。
※ ただ、係数を有理数Qに限る理由はない。
※ 係数を一般的な代数体Kとしても、話の大筋は変わらない。
二次方程式
まずは二次方程式。
二次方程式の2つの答には、√が付く場合、ときには虚数iが付く場合がある。
それらは代数体Q(√n)、あるいはQ(√ni)の上で解くことができる。
一般に、二次方程式の2つの答は異なる数だ。
しかし方程式自体は、2つの答のどちらを入れても、同様に成立する。
二次方程式の係数は、解と係数の関係より、解の基本対称式で表される。
具体的には、x^2 + a x + b = 0 の2つの答をα、βとすると、
- a = α+β
b = αβ
方程式の係数が、答の入れ替えに対して全く動かないということが、見て取れるだろう。
二次方程式を解くという操作は、答の入れ替えに対して不動のものから、
変化するものを生み出す操作なのだ。
★ 方程式を解くためには、答を入れ替えても全く変わらないような原料から、
入れ替えて変わる結果を作り出さなければならない。
入れ替えても結果が変わらないという性質を「対称性」と言う。
基本対称式は、対称性を有している。
それでは、二次方程式を解く過程において、どこで対称性は破れるのか。
それは、べき根√を取る操作においてである。
例えば x^2 - 2 = 0 の答は、+√2 と -√2 の2つになる。
ここで、+ を採るか、- を採るかという2つに1つの選択が、対称性を破っているのだ。
べき根√以外の操作、+-×÷の四則演算では、対称性を破ることはできない。
繰り返す。代数的な方法の中で、対称性を破れる操作は、べき根√だけである。
ところで、体とは、四則演算で閉じている数の集合のことだった。
なので、どんなに四則演算を繰り返しても、今ある体の外に出ることはできない。
体を代数的に拡大する方法も、べき根√の添加だけなのである。
二次方程式の場合、有理数体Qに、√n、あるいは √ni を添加することで、
方程式を解くことができる分解体を作ることができた。
このことは同時に、方程式の答の入れ替えという側面から見れば、
√によって式の対称性を破るということでもある。
このように、代数体の拡大と、方程式の対称性の破れは、
べき根√という操作を通じて、全く同じ挙動を示すのだ。
三次方程式
それでは、べき根√によって、代数体、あるいは方程式の群はどのように変わるのか。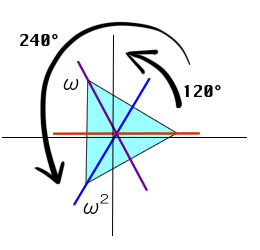 それがはっきりと分かるのは、三次方程式だ。
それがはっきりと分かるのは、三次方程式だ。
いま一度、x^3 - 2 = 0 という基本的な例を取り上げよう。
この方程式の答は、3√2, 3√2ω, 3√2ω^2 の3つ。
方程式が完全に解ける、最小分解体はQ(3√2, √3 i) だ。(ω = (-1+√3i)/2 )
この方程式の群、同時に体の自己同型群といっても同じことだが、それは対称群S3である。
ちょうど正三角形の板を、回転、裏返しによって重ね合わせる操作と同じだ。
3√2 は120度ずつの回転に、√3 i は裏返し操作に相当する。
ここから予想されるのは、べき根n√x が形作る群は、
n角形の回転操作、すなわち位数nの巡回群であるということだ。
複素平面上で、1のn乗根がどのような形をしていたか、思い出してごらん。
それらは複素平面の円周上をn等分していただろう。(数学夜話 第3回)
★ 1のn乗根をωn とする。nは素数に限定する。
体Q(ωn) に、べき根 n√a を添加して体 Q(ωn, n√a) を作る。
Q(ωn)上で、Q(ωn, n√a) の自己同型群は、位数nの巡回群となる。
本来なら証明が必要なところだが、ここでは事実として受け容れることにしよう。
ここで、n乗根のnを素数に限定した。なぜか。
それは、合成数は素数に分解されるからである。
例えば √6 = √2・√3 だ。
なので、√2 と √3 について考えれば、√6 はその組み合わせによって表すことができる。
位数が素数の群は、巡回群しか無い。
三次方程式の解法の本質は、方程式の持つ群S3から素数位数の巡回群を見つけて、くくり出すということなのだ。
注意してほしいのは、方程式の持つ群自体が巡回群だというのではない、ということ。
方程式の群そのものではなくて、方程式の群から部分群を取り出したときにできる商群が巡回群になっている、ということなのである。
群の“差分”とでも言えばわかりやすいだろうか。(差分というより、“商分”なのだが)
体の側から見ると、べき根を加える操作は、もともとあった体に対する“変化”なのである。
たとえば、ある体Kに√2を添加してK(√2) という体を作ったとき、
Kに位数が2の巡回群が“付け加わった”と見るべきなのであって、
必ずしも、もともとの体Kが巡回群である必要はないのである。
三次方程式では、たまたまS3の部分群も、商群も、どちらも巡回群となっているので、このことは解りにくい。
何が巡回群となっているかについては、後で四次方程式を見るときに、改めて振り返ることにしよう。
三次方程式の解法では、6パターンある3つの答の入れ替えを2パターンにまとめるような式、
リゾルベントを構成する必要があった。(数学夜話 第6回)
リゾルベントができれなければ、三次方程式を、より次数の低い二次方程式に帰着させることができない。
幸いにも、三次方程式ではそのようなリゾルベントを作ることができた。
具体的には
(x1 + ω x2 + ω^2 x3) ^ 3
というものだ。
なぜ、このようなリゾルベントを作ることができたのか。
それは、方程式の土台となる数、代数体がS3という対称性を有していたからである。
幸いにも、S3は位数が3の巡回群を部分群に持っていた。
そして、S3をその巡回群で割った余りは、位数が2の巡回群となっている。
これは、もとの方程式がべき根3√と、2√(いわゆる平方根)によって解けるということを示している。
もっとも、体がS3だからといって、具体的なリゾルベントの形がわかるわけではない。
しかし、体がそもそも対称性を有していなければ、その上でどんなに式をいじってみても、
答の入れ替えパターンを減らすようなリゾルベントを作ることはできないはずだ。
四次方程式
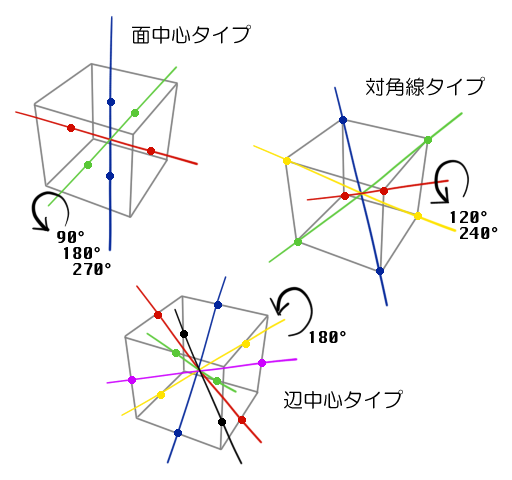
四次方程式の形は、立体に例えるなら立方体、正6面体に相当する。
ただし、四次方程式の4つの答は、立方体の4本の対角線に対応する。
三次方程式の三角形のように、頂点が答に対応しているわけではない。
立方体を回転して、もとの立方体に重ね合わせるやり方は、全部で24通りある。
まず向かい合う面の中心を通る軸が3本。
この軸を中心に、90度回転、180度回転、270度回転がある。
これで、3x3=9通り。(これを“面中心タイプ”と呼ぶことにしよう)
次に、対角線が4本。
それぞれの対角線を中心に、120回転、240度回転がある。
これで、4x2=8通り。(これを“対角線タイプ”と呼ぶことにしよう)
最後に、向かい合う辺同士の中点を結ぶ軸が6本。
この軸を中心に、180度回転がある。
これで、6通り。(これを“辺中心タイプ”と呼ぶことにしよう)
最後に、全く動かない恒等置換が1通り。
全部合わせると、9+8+6+1=24通りとなる。
4つの答の入れ替えである対称群S4の位数は 4! = 24。
S4と、正6面体の入れ替え操作は、余すところなく1対1に対応する。
つまり、対称群S4と、正6面体の回転群は同型である。
対称群S4を、素数位数の巡回群によって、より小さな部分群に分けていってみよう。
単に図形をいじっているかに見えるこの作業が、後で見るように、方程式の解法の本質を表しているのだ。
まず24通りの操作のうち、半分の12通りの操作だけを抜き出してみよう。
ここでは、“面中心タイプ”の中から、90度回転、270度回転を落として、180度回転だけを残すことにする。
これが3通り。
“対角線タイプ”の8通りは全て残す。
“辺中心タイプ”は、全て落とす。
恒等置換の1通りは残す。
残した変換は、3+8+1=12通り。
なぜ、このような恣意的な変換だけを選び取ったのか。
実は、いま残した変換には全て“偶置換”という性質が備わっている。
落とした変換には、全て“奇置換”という性質がある。
“偶置換”というのは、要素を2個ずつ 1->2, 2->1 といった具合にペアで交換していったとき、
変換全体が偶数回のペアの交換と同じになっているということなのである。
たとえば、(2, 3, 4) といった巡回置換は、2と3の交換、続いて2と4の交換、といった2回のペア交換と同じになる。
なので、(2, 3, 4) は偶置換だ。
一方、(1,2,3,4) といった巡回置換は、どうがんばっても3回のペア交換が必要となる。
なので、(1,2,3,4) は奇置換だ。
今行ったように、偶置換だけを集めてきた変換の集合は、これも1つの群となる。
対称群の中から、偶置換だけを集めてできた群のことを“交代群”と言う。
またの新しい用語に、リンの嫌がる顔が目に浮かぶようだが、これも覚えておいてほしい。
S4から作り出した交代群は、A4という記号で表す。
Aは Alternating、交互に、という意味だ。
対称群S4に立方体という形があったように、交代群A4にも、呼応する形がある。
交代群A4の形は、正4面体だ。
対称群S4から交代群A4を生み出す過程は、立方体の動きの中から際だったものを抜き出し、
抜き出した動きによって正4面体という新たな形を再構成するプロセスなのだ。
正4面体を回転して、もとの正4面体に重ね合わせるやり方は、全部で12通りある。
4つの頂点と、向かい合う面の中心を通る軸が4本。
この軸を中心に、120度回転、240度回転がある。
これで、4x2=8通り。(これを“頂点タイプ”と呼ぶことにしよう)
そして、向かい合う辺同士の中点を結ぶ軸が3本。
この軸を中心に、180度回転がある。
これで、3通り。(これを“辺中心タイプ”と呼ぶことにしよう)
最後に、全く動かない恒等置換が1通り。
全部合わせると、8+3+1=12通りとなる。
ところで正4面体の1つの面は、正三角形の板になっている。
正三角形の板と言えば、先ほどの三次方程式を思い出さないか。
実は、ここで出てくる正三角形は、もとの四次方程式で言えば、
解法の途中に出てくる三次方程式に相当しているのである。
さて、交代群A4、あるいは正4面体の回転群を、さらに小さな部分群に分けていってみよう。
ここでは“辺中心タイプ”と恒等置換だけを残して、“頂点タイプ”は全て落とす。 残った操作は、3+1=4通り。
残った操作は、3+1=4通り。
ここで残った操作の形は、3本の直交する軸についての180度回転である。
(もはや立体の多面体にはならない。)
これには“クラインの四元群”という名前が付いている。
クラインの四元群は、ちょうど2x2=4といった関係で、位数が2の巡回群を部分群に持つ。
ここまでで、最初の対称群S4は、すっかり部分群に分けられたことになる。
以上、四次方程式についての流れをまとめると、こんな風になる。
■対称群S4 = 正6面体の回転群 (位数 24 = 4!)
“面中心タイプ
90度, 270度回転 { (1,2,3,4), (1,2,4,3), (1,3,4,2), (1,3,2,4), (1,4,3,2), (1,4,2,3) }
180度回転 { (1,2)(3,4), (1,3)(2,4), (1,4)(2,3) }
“対角線タイプ”{ (1,2,3), (1,3,2), (1,2,4), (1,4,2), (1,3,4), (1,4,3), (2,3,4), (2,4,3) }
“辺中心タイプ”{ (1,2), (1,3), (1,4), (2,3), (2,4), (3,4) }
恒等置換 { e }
▲ S4/A4 = 位数2の巡回群 (24/12 = 2) ▼
■交代群A4 = 正4面体の回転群 (位数 12)
“頂点タイプ” { (1,2,3), (1,3,2), (1,2,4), (1,4,2), (1,3,4), (1,4,3), (2,3,4), (2,4,3) }
“辺中心タイプ”{ (1,2)(3,4), (1,3)(2,4), (1,4)(2,3) }
恒等置換 { e }
▲ A4/V4 = 位数3の巡回群 (12/4 = 3) ▼
■クラインの4元群V4 = 直交する3軸の180度回転 (位数 4)
{ e, (1,2)(3,4), (1,3)(2,4), (1,4)(2,3) }
▲ 位数2の巡回群 (4/2 = 2) ▼
■位数2の巡回群 = 鏡面対称 (位数 2)
{ e, (1,2)(3,4) }
▲ 位数2の巡回群 (2/1 = 2) ▼
■恒等変換
{ e }
べき根による体の拡大、巡回群はどこに相当するのかと言えば、
▲印を付けたところ、いわば“群と部分群の間の変化”に相当している。
たとえば四次方程式で、交代群A4とクラインの4元群V4の間を見ると、その間には位数3の巡回群がある。
この巡回群は、A4からV4という部分群を取り出したときにできる商群であり、
具体的には { e, (2,3,4), (2,4,3) } という、三角形の回転をイメージさせる形となっている。
実際に4次方程式までで登場するべき根は、平方根√と、立方根 3√ までだ。
なので、巡回群と言ってもイメージとしては、三角形の回転までで十分だったのだ。
途中段階にある群、たとえばクラインの4元群などが巡回群となっているわけではない。
それでは、この途中段階にある群は、部分群でありさえすれば、何でもいいのだろうか。
なぜ、上の流れのやり方でなければならないのか?
ひょっとすると、S4から部分群を取り出すやり方は、上の流れ以外にもあるかもしれない・・・
そのように、リンは疑問を感じたかもしれない。
方程式に戻って考えると、途中段階にある部分群は何でもいいという訳ではない。
1つ、外せない重要な条件がある。
それは“途中段階にある部分群が、方程式の持つ全ての答をカバーしていること”なのである。
“答をカバー”するとは、どういうことか。
一般にN次方程式には、N個の答があった。
途中段階で考えている代数体に、そのN個の答が全部含まれていなければ、その代数体は方程式の解法の役に立たない。
答が体からこぼれ落ちてしまうからである。
途中段階で考えている代数体とは、解法の途中に表れる補助方程式に対応している。
もし、途中の体から答がこぼれ落ちてしまったら、補助方程式から最終的な答に達することができなくなってしまう。
代数方程式の持つ複数の答のことを、共役数と言った。
途中段階にある部分群は、全ての共役数を含むような、体の同型写像でなければならないのだ。
代数体という側面から考えると、たとえば Q(3√2) という体は x^3 - 2 = 0 という方程式の全ての答をカバーしていない。
なので、こうした拡大は解法の上で、あまり意味が無い。(数学夜話 第10回)
Q(3√2, ω) という体には意味がある。
この体は、 x^3 - 2 = 0 という方程式の全ての答をカバーしている。
では、全ての答をカバーしているような群とは、どのような形をしているのだろうか。
結論を先に言えば、途中段階にある部分群が“正規部分群”となっているとき、方程式の答は全てカバーされる。
正規部分群とは a * H = H * a のように、元を右からかけても、左からかけても一致するような部分群のことであった。
可換群であれば、この正規部分群という条件は自ずと満たされる。
そもそも有限群は有限個の元しか持たないのだから、片っ端から掛け合わせてゆけば、いつかは一巡して元に戻る。
この一巡に合わせて、方程式のある1つの答を、体の同型写像に従って次々に変換してゆけば、
最初の1つの答は、残りの答の全てをカバーするかのように見える。(数学夜話 第10回)
これまで例に挙げてきた、+√2 → -√2 → +√2、1 → ω → ω^2 → 1 といった入れ替えがそうだ。
しかし、ここでもし仮に、一巡する経路が1つに定まらなかったとしたら、どうなるだろうか。
例えば 1 → ω → ω^2 → 1 という経路と、1 → ω' → ω'^2 → 1 の2つが存在するとしたら、
方程式の答は2種類にブレてしまって、1つに定まらなくなるだろう。
そんなことが実際に起こり得るのだろうか。
一般に、群というものは可換ではなかった。 a * b ≠ b * a
三角形の回転と裏返しを取り上げてみても、可換ではない。
もし、右回りの経路と、左回りの経路が異なるものであったなら、答は2種類にブレてしまう。
ここで、右剰余類と左剰余類という性質が思い浮かぶ。
もし右剰余類と左剰余類が異なっていたら、類別が2系統できてしまう。
それはちょうど、2種類にブレた経路が存在する状態でもある。
なので、少なくとも正規部分群でなければ、方程式の持つ全ての答はカバーできないだろう。
群という見方によって、方程式が代数的に解ける条件というものが明らかになってきた。
N次方程式の答の入れ替えが作る群は、対称群Snである。
その対称群Snが、次のような仕方で順次部分群に分けられるとき、もとの方程式は解ける。
1.もとの群から、正規部分群が取り出せること。
(答が全て、体に含まれていること)
2.正規部分群を取り出したときにできる商群が、素数位数の巡回群となっていること。
(べき根という操作によって解けること)
3.1.2.の仕方で次々と作っていった部分群の系列が、最後には恒等変換{e}に達すること。
(最後には完全に解けること)
五次方程式
これで、いよいよ最後の目標であった、五次方程式にとりかかることができる。
ここまで来るのは、本当に長い道程だったと思う。
しかも、まだ数多くの疑問を残しているかもしれない。
僕だって、全てを余すところなく説明してきたわけではない。
それでも、リンはきっと、目に見えない“五次方程式の形”について、
なんとかイメージできるところまで来ていることだろう。
五次方程式の群は、対称群S5だ。
S5を直接表せるような正多面体は存在しないが、
S5の中から偶置換を取り出した交代群A5であれば、正多面体として描くことができる。
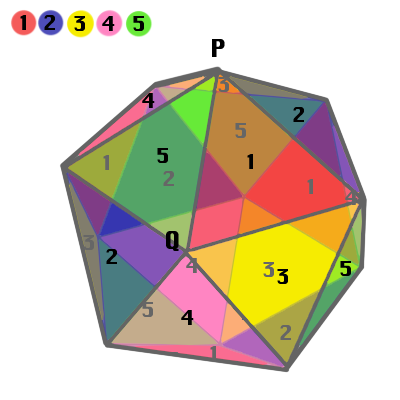
交代群A5は、正20面体に相当する。
正20面体を、A5に対応付けるルールは少々複雑だ。
正20面体のそれぞれの面を、5色に塗り分ける。
そのとき
・辺を共有して隣り合っている2つの面の色は必ず異なるように、
・1つの頂点に集まる5つの面の色が全て異なるように、
色を付ける。
そのような塗り分け方の1つを、図に示した。
ある1つの頂点Pに集まるそれぞれの色に、赤=1, 青=2, 黄=3, 桃=4, 緑=5 といった数字を割り当てる。
正20面体を回転して、Pを別の頂点に重ね合わせたとき、もともとPの周りにあった[1,2,3,4,5]という数字の並びは、
移動先の数字の並びに重なることになる。
例えば、Pを、図のQに重ねたとき、[1,2,3,4,5] は [4,3,1,5,2] に置き換わる。
このような1つの重ね合わせが、1つの置き換え操作を表すことになる。
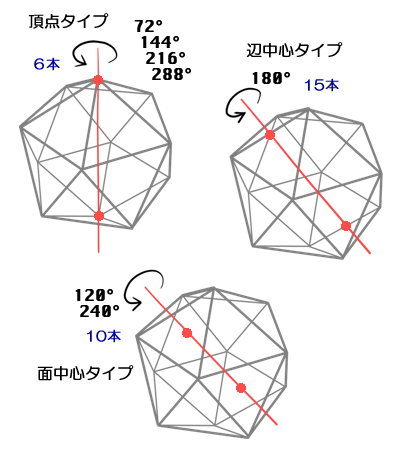
正20面体には12個の頂点がある。
各頂点について、72度=2π/5回転ずつ、5通りの回転がある。
なので、重ね合わせ操作は、全部で 12 * 5 = 60 通りとなる。
実は、塗り分けの方法は、本質的には2種類ある。
それが、ここに表れる群が対称群S5ではなくて、対称群A5となっている理由だ。
5つの要素の置き換えパターンは、全部で 5! = 120通り。
一方、1つの正20面体上で表現できる置き換えパターンは 60通りしかない。
塗り分け方の異なる、もう1つの正20面体を用意して、
この2つの正20面体の間を自由に行き来できるようにしたら、全体として対称群S5を表すことになるだろう。
正20面体を回転して、もとの正20面体に重ね合わせるやり方は、全部で60通りある。
向かい合う頂点同士を通る軸が6本。
この軸を中心に、72度回転、144度回転、216度回転、288度回転がある。
これで、6x4=24通り。(これを“頂点タイプ”と呼ぶことにしよう)
向かい合う辺同士を通る軸が15本。
この軸を中心に、180度回転がある。
これで、15x1=15通り。(これを“辺中心タイプ”と呼ぶことにしよう)
向かい合う面同士の中点を結ぶ軸が10本。
この軸を中心に、120度回転、240度回転がある。
これで、10x2=20通り。(これを“面中心タイプ”と呼ぶことにしよう)
最後に、全く動かない恒等置換が1通り。
全部合わせると、24+15+20+1=60通りとなる。
五次方程式を解くとは、この60通りの回転操作の中から、素数位数の巡回群を割り出して、正規部分群を見出す作業となる。
そして結局のところ、そのような正規部分群は見つからないのだ。
60の約数には、次のものがある。
30x2
20x3
15x4
12x5
10x6
素数位数という条件からすると、候補に挙がるのは2,3,5の3つだ。
2の場合、
60通りの回転操作の中から、30通りだけを抜き出せということなのだが、果たしてそれが可能だろうか。
下の表を見て、考えてみてほしい。
頂点タイプ: 24通り
辺中心タイプ: 15通り
面中心タイプ: 20通り
恒等置換: 1通り
どれか1つのタイプだけを取り出したところで、30通りにはならない。
タイプをまたがって、たとえば辺中心タイプの15通りと、頂点タイプの中から14通り、
それに恒等置換1通りで、合計30通りといった組み合わせが考えられるかもしれない。
(恒等置換の1通りは、必ず含まなければならない)
しかし、これだと頂点タイプの中から、どの14通りを取り出せばよいのだろうか。
5角形に回転する頂点の形から考えて、その中の一部を取り出すには、無理があるだろう。
このようにしてみると、30通りだけの操作を抜き出すことは、どうもできそうにない。
他の約数についても同様だ。
3の場合、60通りの回転操作の中から、20通りだけを抜き出すことになる。
面中心タイプの20通りではだめだ。そこには恒等置換が含まれていない。
5の場合、60通りの回転操作の中から、12通りだけを抜き出すことになる。
恒等置換を除けば、残る11通りを探すことになるのだが、あてはまる回転操作は何処にも無さそうだ。
五次方程式の謎は、正20面体の形によって解き明かされる。
驚くべきことではないか。
リンにとってはまだ、謎は依然として残ってるかもしれない。
ここに書いた直感的な説明だけでは、数学的に厳密な証明に程遠いかもしれない。
それでも、たとえ数学的な厳密さを損なっていたとしても、
僕はリンに、何よりも数学の持つ形の美しさを伝えたかった。
複素数、方程式、代数体、群。
数学は、形の美しさに満ちている。
直接目に見えない形を想像するのは、楽しく、不思議な体験だ。
最後に、もう1つだけ不思議なことを伝えておこう。
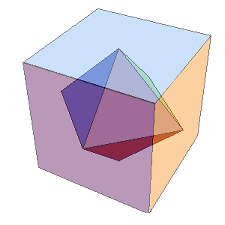
正6面体の、隣り合う面の中心同士を線で結んでゆくと、その中に正8面体が出現する。
反対に、正8面体の隣り合う面の中心同士を線で結んでゆくと、その中に正6面体が出現する。
正6面体と正8面体は、群として見れば、同じ構造を有しているのだ。
同様に、
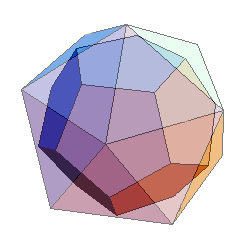
正20面体の、隣り合う面の中心同士を線で結んでゆくと、その中に正12面体が出現する。
反対に、正12面体の隣り合う面の中心同士を線で結んでゆくと、その中に正20面体が出現する。
正20面体と正12面体は、群として見れば、同じ構造を有している。
これで五次方程式までの話の中に、全ての正多面体が登場したことになる。
正4面体、正6面体、正8面体、正12面体、正20面体。
方程式に隠れた見えない形の美しさを、感じ取ってほしい。










1 Comments:
天才数学者はこう解いた、こう生きた (講談社選書メチエ) 単行本(ソフトカバー) – 2001/11/9
木村 俊一 (著)
5つ星のうち 4.0 12件のカスタマーレビュー
5つ星のうち4.0名著なのでおどろいた
2006年4月7日
形式: 単行本(ソフトカバー)Amazonで購入
この本は、出版社の意図と、著者の意図が食い違っているため、全体に構成がおかしいが、(部分的にではあるが)名著と言ってもいいと思う。特に正十二面体(それぞれの面が正五角形)と五次方程式の解の関係については目から鱗が落ちる指摘で、誰かネットで詳しく説明する人が欲しいくらいだ(文部科学省にやってもらいたい)。複素平面という一般になじみのないコンセプトもこうした教え方なら受け入れられるだろう。
部分的にではあるが、著者の代数幾何の射程の広さに数学教育の未来を垣間見せてくれた名著である。
14人のお客様がこれが役に立ったと考えています
コメントを投稿
<< Home