【数学】イーノック教授「リーマン予想を解いた」と主張

リーマン予想：
　　　　　　　　　∞？
　　　　　　虚部　｜
　　　　　　　｜　｜
　　　　　　　｜　｜
＿＿＿＿＿＿＿｜＿｜＿＿＿
　　ー１　　０｜　｜　１　　実部
　　　　　　　｜　｜
　　　　　　　｜　｜
　　　　　　　　１／２

>素数の研究の関連で特定の方程式が出て（素数自体の導出式イコールではない）、
>その式（ ｘ何ちゃら=0 になるxの値) の解はxが複素数だとたくさんあるところ、
>全部　x= 0.5 + t*i （tはいろんな値、iは虚数）になるだろう、ということ
>x= 0.35+ 23i とか、 101+5.6i　とかになることは絶対になく、
>0.5+?i というふうに0.5だけ

 ゼータ関数：
 ｙ＝１／ｘ^ｓ
 　　
ｙ｜　。
　｜　｜。
　｜　｜　　。
　｜　｜　　｜　　。　　　　
＿｜＿｜＿＿｜＿＿｜＿＿｜＿＿
０　　１　　２　　３　　４　　ｘ

Re(s)>1 の場合、
1+(1/2^s)+(1/3^s)+(1/4^s)+(1/5^s)+(1/6^s)+・・・・・
(sは複素数)
の形をゼータ関数という

http://anago.2ch.net/test/read.cgi/scienceplus/1447825632/

【数学】イーノック教授「リーマン予想を解いた」と主張　©2ch.net
17 ：名無しのひみつ＠転載は禁止：2015/11/18(水) 15:12:34.88 ID:/eaZ7taW
>>10
素数が出てくる規則を求める式をリーマンが考えた
この式が正しいことを証明すれば解決

で、OK?　数学に詳しい人確認して



71 ：名無しのひみつ＠転載は禁止：2015/11/18(水) 18:39:35.70 ID:B+SF11iA
>>17
ちょっと違うだろうな
ウィキに書いてあるとおりだが、素数の研究の関連で特定の方程式が出て（素数自体の導出式イコールではない）、
その式（ ｘ何ちゃら=0 になるxの値) の解はxが複素数だとたくさんあるところ、
全部　x= 0.5 + t*i （tはいろんな値、iは虚数）になるだろう、ということ　（ベタに数値実験するとそうなる）

x= 0.35+ 23i とか、 101+5.6i　とかになることは絶対になく、 0.5+?i というふうに0.5だけ

式の形からして、左のようないろいろ乱雑なものになっても全然よさそうなところ、0.5に統一される、というところの不思議
しかしその証明が天才数学者総がかりで一世紀半解けない

現代数学最先端の数論幾何、グロタンディークとか望月教授の分野も、ある面いずれそれを解くことを横目でにらみながら、物凄い高難度抽象システムを延々作り上げて来たといっていいほど


146 ：名無しのひみつ＠転載は禁止：2015/11/19(木) 20:49:25.55 ID:1FyUb5R1
その前に

1+(1/2^s)+(1/3^s)+(1/4^s)+(1/5^s)+(1/6^s)+・・・・・
(sは複素数)

の形をゼータ関数という、という辺りから
スレ内で説明した方が良いんじゃないかなあ？

いきなり素数の話になって
そこから更にSSL認証通信のRSA暗号が全部丸見えだぜ～って話になってもなあ


196 ：名無しのひみつ＠転載は禁止：2015/11/22(日) 08:58:45.45 ID:be4xJHc5
>>193
ゼータ関数が
ζ(s) = 1^(-s) + 2^(-s) + 3^(-s) + …
と書けるのは Re(s)>1 の場合のみよ。

http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1136066801

oga4930さん

2010/1/3116:11:10

ゼータ関数とはなんですか？

数学に興味があるので、詳しく教えてください。
他にもいろいろ教えてください。
中3でも分かりやすくお願いします。多少難しくてもいいです。

xy平面（普通の座標平面）を書いてみてください。
このグラフ上で、
x=0以外では、y=0
x=0のところだけでは、yはどこまでも大きくなる
という関数が、ゼータ関数です。
x=0のところで、yがどこまでも大きい、というのは、その平面状の、すべてのxの範囲での積分という操作をすると、面積が1になる、ということなのですが、どういうことか、おおよその説明をします。
（範囲が決まっている）積分、というのは、（定積分と呼びますが）簡単に言えば、x軸とその関数のグラフとの間にはさまれている面積を求める、ということ です。もちろん、面積、ということは、直線とか曲線とかで全方向を囲まれていなければ決まらないので、左と右の端を決めます。つまり、ある関数のグラフ （y=x^2とか）と、x軸との間で囲まれた部分の、ある範囲（x=3からx=6までの間とか）の面積を求めることを、（x=3からx=6の範囲で）積分 する、と呼ぶわけです。
このとき、横の範囲は、考えているのですが、限りなく左にある左端から、限りなく右にある右端までの範囲で積分する（つまり、その平面全体での面積を求める）と、ゼータ関数は、その値が1になります。
普通、長方形の面積って、横の長さ×縦の長さで求めますよね。
しかし、ゼータ関数というのは、はじめに言ったとおり、x=0のときだけ値が0より大きいので、横の長さがありません。というか、横の長さは0で、縦の長 さが?の長方形の面積と同じだと思えるわけですね。だから、縦の長さはいくら大きくても足りませんが、いくらでも大きければ、面積が出てくるんじゃない か、という風に思うわけです。（実際は、もっと厳密に考えるのですが、おおよそのイメージとしてはこんな感じです）。

あと、その使い道ですが、
関数f(x)に、ζ(x)をかけて、x=-∞からx=∞の範囲で積分すると、f(0)の値が出てきますね。なぜかというと、ζ（ゼータと読む）関数は、積分した時、x=0のときだけ面積が1になるからです。
という使い方ができます。

 http://mathtrain.jp/riemannyoso

リーマン予想の意味

リーマン予想の主張を解説します。

• ・ゼータ関数ζ(z)というのは1以外の複素数全体で定義された関数です。実部が1より大きい複素数zに対してはζ(z)=∑n=1∞1nzという美しい式で定義されます。→ゼータ関数の定義と基本的な話
• ζ(z)=0となる複素数zをゼータ関数の零点と言います。
• ζ(−2)=ζ(−4)=⋯=0が成立することが（ζ関数にある程度精通している人にとっては）簡単に分かるので負の偶数は自明な零点と呼ばれます。

以上を踏まえると，リーマン予想は

ζ(z)=0となるならばzは負の偶数，またはzの実部が12である。

と言うこともできます。

分かっていること

事実1：虚部が小さい方から10兆個の非自明な零点は実部が12であることが計算されています。Xavier (2004)
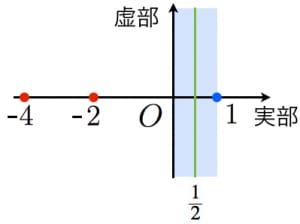
事実2：実部が12である零点が無限個存在することも証明されています（緑の直線上に零点が無限に存在する）。
事実3：非自明な零点の実部は0より大きく1より小さいことが証明されています（非自明な零点は青い領域にある）。

素数との関係

n以下の素数の個数をπ(n)と書きます（パイ関数）。
このとき，π(n)はnが十分大きいときnlognで近似できます（素数定理）。→整数論の美しい定理7つ
実は，リーマン予想よりも弱い主張（上記の事実3）を認めるだけで素数定理が比較的容易に証明できます。さらに，リーマン予想が正しいとしたら素数定理の近似精度に関するよりよい理論保証が与えられます。そのような意味でリーマン予想と素数分布は関係しています。

RSA暗号との関係

最後に，リーマン予想と暗号の関係についてです。
RSA暗号の安全性の根拠は素因数分解の難しさです。→素因数分解の難しさと素数判定
しかし，リーマン予想が証明されたからと言って大きな数の素因数分解が現実的な計算時間でできるようになる訳ではありません（少なくとも僕の知っている＆調べた限りでは）。
正：リーマン予想が証明される→素数分布の性質が（π(x)の近似精度の改善という意味で）詳しく分かる
誤：リーマン予想が証明される→RSA暗号が突破できる(^O^)

NHKスペシャル「魔性の難問 ～リーマン予想・天才たちの闘い～」という番組では上記の「誤」があたかも正しいかのような説明の仕方をしていたので残念でした。

http://mathtrain.jp/zetafunction

ゼータ関数の定義と基本的な話

分野: 解析 　レベル: ★マニアック

---

s>1なる実数に対してゼータ関数ζ(s)は以下のように定義される：
ζ(s)=∑n=1∞1ns=11s+12s+13s+⋯

（リーマンの）ゼータ関数のごく基本的な話をざっくりと解説します。

ゼータ関数の値の存在

まずは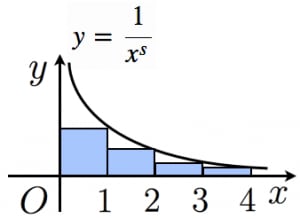1より大きい任意の実数sに対してζ(s)がちゃんと存在することを証明しておきます。すなわち，無限級数∑n=1∞1nsが収束することを示します。

証明

y=1xsのグラフを書いて1+12s+13s+⋯を図示してみると，以下の不等式が成立することが分かる：
∑n=1k1ns<1+∫k1dxxs
実際に右辺を計算すると，
1+[x1−s1−s]k1=1+k1−s−11−s
1−s<0に注意してk→∞の極限を取ると，
∑n=1∞1ns<1+1s−1
を得る。よって，ζ(s)は収束して（注）その値は1+1s−1以下。

注：単調増加で上に有界な数列は収束することを使いました。

複素数に広げる

実数の複素数乗は定義できる（→複素数の対数関数とiのi乗が実数であること）ので冒頭の式はsが複素数でも意味を持ちます。
実際，実部が1より大きい複素数sに対して∑n=1∞1nsは収束することが知られています。
すなわち，冒頭の表式を使うことで実部が1より大きい複素数全体についてゼータ関数の値が定義できました。
しかし，残念ながら実部が1以下である複素数sに対しては∑n=1∞1nsは発散してしまいます。例えばs=1のとき：調和級数1+1/2+1/3…が発散することの証明

解析接続

ゼータ関数の定義域をさらに広げるためには解析接続という方法を使います。
解析接続の詳細はここでは説明しませんが，ざっくり言うと
複素数平面上のある領域で定義された関数を，いい感じに延長して定義域を広げることです。

例えば，実軸上の一部で定義された赤い関数をいい感じに延長すると（赤＋青）という関数が得られます。（赤＋緑）もいい感じの関数に見えますが，解析接続における「いい感じの関数」とは「正則関数」という非常に強い性質のものであるため，解析接続は一意に定まります。

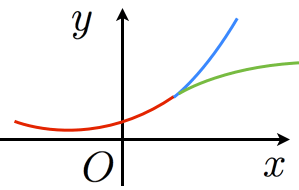
ゼータ関数の解析接続

ゼータ関数はs≠1なる複素数全体に解析接続できることが知られています。つまり，ゼータ関数の定義域はs≠1なる複素数全体。s=1はゼータ関数の極，と言うことができます。
これでゼータ関数を定義できたのですが「∑n=1∞1nsを解析接続したもの」と言っても実際の値がよく分かりません。そこで，1と異なる任意の複素数sに対してζ(s)=(sの簡単な式)みたいなものが欲しくなりますが（少なくとも自分の知識では）そのような簡単な式はありません。
解析接続をした具体的な式はベルヌーイ数を用いて表す方法や，ガンマ関数を用いて表す方法などがあるようですが，いずれも複雑だったり場合分けが必要だったりします。

ゼータ関数のいくつかの値

・ζ(2)=π26
これは平方数の逆数和の話です。→バーゼル問題の初等的な証明
・ζ(−1)=−112
ζ(s)=∑n=1∞1nsという式はsの実部が1より大きいときにしか意味を持ちませんが，この式の両辺に強引にs=−1を代入すると，
1+2+3+4+⋯=−112という奇妙な式が得られます。この奇妙な式は間違いですが，有名です。
・ζ(−2)=ζ(−4)=ζ(−6)=⋯=0
ゼータ関数に負の偶数を代入すると0になります。これを自明な零点と言います（素人にとっては全然自明じゃないですが、、）。

リーマン予想についてはそのうち別記事で書きたいなあと思っています。

追記：→リーマン予想の意味，素数分布との関係

フーリエ級数展開の公式と意味

分野: 解析 　レベル: ◎大学数学

---

フーリエ級数展開：
f(x)が周期Tの「まともな」関数なら
f(x)=a02+∑n=1∞(ancos2πnxT+bnsin2πnxT)
ただし，
an=2T∫T0f(x)cos2πnxTdx
bn=2T∫T0f(x)sin2πnxTdx

フーリエ展開の意味，係数の導出，応用例としてπ26に収束する有名な級数の話を解説。

フーリエ級数展開とは

〜やりたいこと〜
与えられた周期Tの関数を，周期T（の約数もOK）の三角関数（サインとコサイン）の和で表現したいという話です。
〜なぜ2πnxTが登場するのか〜
・g(x)=sin2πnxTの周期はTnであり，g(x+T)=g(x)を満たします。h(x)=cos2πnxTも同様です。そこで，これらの「Tズラしてもとに戻る単純な関数の無限和」で「Tズラしてもとに戻る関数f(x)」を表現します。
特に，f(x)の周期が2πの場合，使う三角関数はsinnx,cosnxとシンプルな形になります。

フーリエ級数展開の条件

冒頭では「まともな」関数と述べてぼかしました。やばい関数だとフーリエ級数展開できませんが，応用上登場する関数はだいたいフーリエ級数展開できるのでそんなに気にしなくてOKです。
例えばf(x)が連続かつ導関数も連続なら問題なしです。f(x)やf′(x)に不連続点がちょいちょいあっても問題なし（不連続点以外で各点収束）です。
フーリエ級数展開できるための詳しい条件については専門書を参照して下さい。

フーリエ係数の導出

フーリエ係数an,bnの形がなぜ冒頭の式で表されるのか説明します。三角関数の積分にある程度慣れている必要があります。

（係数の導出）
〜a0について〜
f(x)=a02+∑n=1∞(ancos2πnxT+bnsin2πnxT)
の両辺を0からTまで積分すると（右辺の周期関数の積分が全て0になるので），∫T0f(x)dt=a02T
つまり，a0=2T∫T0f(x)dt
〜an（n≥1）について〜
f(x)=a02+∑n=1∞(ancos2πnxT+bnsin2πnxT)
の両辺にcos2πnxTをかけて0からTまで積分すると，∫T0f(x)cos2πnxTdx=an2T（→注1）
よりan=2T∫T0f(x)cos2πnxTdx
〜bnについて〜
同じように両辺にsin2πnxTをかけて0からTまで積分するとOK。

注1：三角関数の直交性という積分公式を用いています。→三角関数の積の積分と直交性
この公式により右辺の各項の積分はほとんど0になり，∫T0ancos22πnxTdx=an2Tだけが生き残ります。
注2：なお，積分と無限和の順序交換が可能であることを仮定しています。この部分が厳密ではありませんが，フーリエ係数の形の意味を見るには十分でしょう。
なお，フーリエ展開には複素指数関数を用いた表現もあります。→複素数型のフーリエ級数展開とその導出

具体例

例題

y=x2(−π≤x≤π)を周期2πの関数になるように拡張した関数 f(x) のフーリエ級数展開を求めよ。

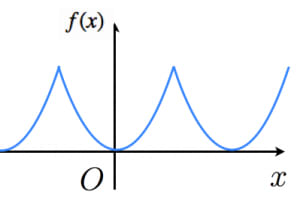
解答

フーリエ係数を求める。周期性に注意すると0から2πまでの積分値は−πからπまでの積分値と等しいことが分かる。
a0=22π∫π−πx2dx=23π2
an=22π∫π−πx2cosnxdx，瞬間部分積分を用いて計算するとan=(−1)n4n2
bn=22π∫π−πx2sinnxdxであり，被積分関数は奇関数なのでbn=0
つまり，f(x)=π23+∑n=1∞(−1)n4n2cosnx
ちなみにこの式にx=πを代入するとπ2=π23+4∑n=1∞1n2
となり，有名な級数∑n=1∞1n2=π26を得ます。→バーゼル問題の初等的な証明

フーリエ展開を使えば他にもいろいろな級数が導出できます！

調和級数1+1/2+1/3…が発散することの証明

分野: 極限，微分 　レベル: ★最難関大学

---

1+12+13+…=∑k=1∞1k=∞

1nをどんどん足していくと無限大に発散するというのは非常に有名な公式です。この公式を背景とする入試問題もたまに出題されるので証明方法と一緒に覚えておきましょう。
一般的に無限級数の評価は

1，式変形による等式変形，不等式評価
2，積分を用いた不等式評価

のいずれかの方法で行います。この公式の場合はどちらの方法も通用します。

1：1+1/2+1/3+…を不等式で下からおさえる方法

おそらく一番有名な方法です。エレガントです。

証明

1+12+13+14>1+12+(14+14)=1+12+12
1+12+13+14+15+16+17+18>1+12+(14+14)+(18+18+18+18)=1+12+12+12
この変形を一般化すると，以下の不等式が得られる：
∑k=12p1k≥1+p2
p→∞とすると右辺は発散するので左辺も発散する。
以上から題意は証明された。

2：1+1/2+1/3+…を不等式で下からおさえる方法その2

指数関数の有名不等式ex≥1+xを用いた方法もあります。（→指数関数のマクローリン型不等式）
Honsbergerによって発見された証明です。

証明

exp(1+12+13+14+⋯+1n)=exp(1)exp(12)exp(13)exp(14)⋯exp(1n)≥(1+1)(1+12)(1+13)(1+14)⋯(1+1n)=2⋅32⋅43⋅54⋅⋯⋅n+1n=n+1
よって，∑k=1n1k≥log(n+1)
n→∞とすると右辺は発散するので左辺も発散する。

ちなみに，証明で用いた不等式の差の極限は収束することが知られており，その収束先をオイラー定数といいます。

オイラー定数：γ=limn→∞(∑k=1n1k−log(n+1))=limn→∞(∑k=1n1k−logn)

ただし、最後の等号は
limn→∞(log(n+1)−logn)=limn→∞log(n+1n)=0
より成り立つ。

3：積分を用いた1+1/2+1/3+…の発散証明

無限級数の評価で積分を用いるのは定石です。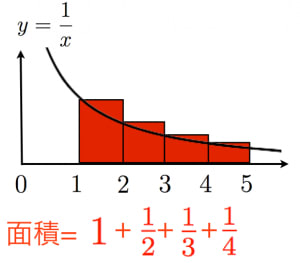

証明

右の図より，∑k=1n1k≥∫n+111xdx=log(n+1)
となり方法2で導いたものと同じ不等式が得られる。
nを無限大に飛ばすことで題意は示される。

ちなみに，図の赤い部分においてy=1xよりも上側にはみ出た部分の面積を足し上げていくとオイラー定数になります。この図からオイラー定数が0.5より大きくて1よりも小さいことが分かります。
ちなみに，分数を交互に足し引きして1−12+13−⋯とした場合には交代級数と呼ばれ，その値はlog2に収束することが知られています。
→log2に収束する交代級数の証明

小学生でも意味が分かる奥深い問題だからこそおもしろい

バーゼル問題の初等的な証明

分野: 極限，微分 　レベル: ★マニアック

---

バーゼル問題：平方数の逆二乗和はπ26に収束する。つまり，
∑k=1∞1k2=1+14+19+⋯=π26

平方数の逆二乗和はいくつに収束するのか？という問題がバーゼル問題です。高校数学で理解できるバーゼル問題の証明を解説します。

級数が収束すること

一般に，ζ(p)=∑k=1∞1kpをリーマンのゼータ関数といいます。p=1のときは発散します。→調和級数1+1/2+1/3…が発散することの証明
バーゼル問題はp=2のときのゼータ関数の値を求める問題です。
まず，この級数が発散せずに収束することは以下のように簡単に証明できます。非常に有名なテクニック：→部分分数分解など差に分解する4つの恒等式を用いて級数を上からおさえます。

証明

1+122+132+⋯+1n2<1+11⋅2+12⋅3+⋯+1(n−1)n=1+(1−12)+(12−13)+⋯+(1n−1−1n)=2−1n より，バーゼル問題の級数は収束してその値は2以下であることが分かる。

バーゼル問題の証明の道具

バーゼル問題の級数の収束先がπ26であることの証明はいろいろな方法があります。特に，サインのマクローリン展開および無限積展開を用いるオイラーの方法が有名です。
ここでは，大学数学の道具を使わず高校数学で理解できる方法で証明します。
使う道具は以下の3つです：

1：0≤x≤π2においてsinx≤x≤tanx（有名不等式）
2：(cosθ+isinθ)n=cosnθ+isinnθ（ド・モアブル）
3：解と係数の関係

1についてはsinx/xについて覚えておくべき2つのこと，
2については，ドモアブルの定理の意味と証明を参照して下さい。

バーゼル問題の証明の前半

まずは部分和1+122+⋯+1n2を上と下から三角関数ではさみます。

証明の前半

k=1,2,⋯,nに対してθk=kπ2n+1とおく。0≤θk≤π2より，
sinθk≤θk≤tanθkを得る。
各辺の逆数をとって二乗すると，
1tan2θk≤(2n+1)2k2π2≤1sin2θk
これを変形して平方数の逆数を作り出す：
π2(2n+1)2⋅1tan2θk≤1k2≤π2(2n+1)2(1+1tan2θk)
これをk=1からnまで足し合わせる：
π2(2+1n)2n2∑k=1n1tan2θk≤∑k=1n1k2≤π2(2+1n)2(1n+1n2∑k=1n1tan2θk)⋯(※)
よって，あとはlimn→∞1n2∑k=1n1tan2θk=23を証明すれば，上記の不等式の極限を取ってハサミ打ちの原理を使うことにより収束先がπ222×23=π26であることが分かる。

(※)補足：最右辺第一項は1をn個足しあわせているので，1n2∑k=1n1=nn2=1nとなっている。

証明の後半：東工大の入試問題

目標はlimn→∞Snn2=23です。ただし，Sn=∑k=1n1tan2θk
これは，1990年東工大後期第二問と本質的に同じ問題になります。（東工大の入試問題では誘導がついていました。）
ド・モアブルの定理と解と係数の関係を使います！

証明

sin(2n+1)θk=0より，
z=(cosθk+isinθk)2n+1の虚部は0である。
また，sinθk≠0なので，zをsin2n+1θkで割ることにより，
z′=(1tanθk+i)2n+1の虚部は0である。
このz′の虚部は1tan2θkのn次多項式とみなせる！
つまり，このn次多項式を
f(x)=anxn+an−1xn−1+⋯+a0=0とおくと，k=1,2,⋯,nに対して
f(1tan2θk)=0である。
すなわちn次方程式f(x)=0の解がn個全て構成できたので解と係数の関係より，
Sn=−an−1an
実際，二項定理を用いて計算すると，
an=2n+1,an−1=−(2n+1)(2n)(2n−1)6なので
Sn=n(2n−1)3
よって，limn→∞Snn2=23が示された。

なお，フーリエ展開を用いた別証もきれいです！→フーリエ級数展開の公式と意味の記事末

思ったより長く険しい証明になってしまいました。

Tag: 無限和，無限積の美しい公式まとめ