物理学:インデックス
http://nam-students.blogspot.jp/2013/02/blog-post_1381.html
Raum und Zeit (Minkowski) 1908
http://nam-students.blogspot.jp/2012/01/raum-und-zeit-minkowski1908.html
ハドロンの分類図、SU(3)の図
http://nam-students.blogspot.jp/2015/12/su.html?m=0(本頁)
NAMs出版プロジェクト: モジュラー形式:メモ
http://nam-students.blogspot.jp/2016/03/blog-post_20.html
A 1940 Letter of André Weil on Analogy in Mathematics
http://nam-students.blogspot.jp/2017/06/a-1940-letter-of-andre-weil-on-analogy.htmlハドロンの分類図:強い力
Those 8 dimensions correspond to the 8 particles in the so-called "baryon octet"
(陽子proton, 中性子neutron, Σ+, Σ0, Σ−, Ξ−, Ξ0, Λ).
(udd) Y (uud)
中性子 n0____|____P+ 陽子
/\ |1 /\
/ \ | / \
/ \ | / \
/ \|/ \
ーー〈ーーーーーーーーXーーーーーーーー〉ーー
Σ ー \ー1/2 Σ 0|λ0 ー1/2 /Σ+
ー1 \ / | \ / 1
\ / | \ /
\/___|___\/
三ー |ー1 三0
(udd) Y (uud)
中性子 n0____|____P+ 陽子
/\ |1 /\
/ \ | / \
/ \ | / \
/ \|/ \
ーー〈ーーーーーーーーXーーーーーーーー〉ーー
Σ ー \ー1/2 Σ 0|λ0 ー1/2 /Σ+
ー1 \ / | \ / 1
\ / | \ /
\/___|___\/
三ー |ー1 三0
物理
と
数学
y|
|p
____|____
/\ | /\
q/U+\ | /V+\q
/ \ | / \
/ \|/ \
ーー〈Tー ーーーーーXーーーーー T+〉ーー→
\ /|\ / t
\ / | \ /
p \Vー/ | \Uー/ p
\/___|___\/
|q
:SU(3)の図
奇妙な一致。
Y
中性子 n0____|____P+ 陽子
/\ |1 /\
/ \ | / \
/ \ | / \
__/______\|/______\__
Σ ー \ー1/2 Σ 0|\λ0 ー1/2/Σ+
ー1 \ / | \ / 1
\ / | \ /
\/___|___\/
三ー |ー1 三0
クォークモデルは、1950年代から1960年代に渡って発見された非常に多くのハドロンを系統立てて分類するために開発され、1960年代後半から現在までの実験によってその正しさが検証されている。これらの実験的証拠により、ハドロンは"基本粒子"ではなく、それを構成する"価クォーク"が基本粒子であると考えられている。クォークモデルは価クォーク単位でハドロンを分類する。価クォークとは、ハドロンの量子数の実体を担っているクォークおよび反クォークである。
これらの量子数はハドロンの種類を同定するためのラベルであり、二種類に分けることができる。一つは、ポアンカレ対称性を持つJPCである。ここで、J、PおよびCはそれぞれ全角運動量、パリティ対称性およびチャージ対称性である。二つ目は、アイソスピン、ストレンジネスおよびチャームなどのフレーバー量子数である。クォークモデルは八道説の分類法に従っている。(#中間子および#バリオン参照)
全てのクォークにはバリオン数1⁄3が割り当てられている。アップ、チャームおよびトップクォークは電荷+2⁄3を持ち、ダウン、ストレンジおよびボトムクォークは電荷−1⁄3を持つ。また、反クォークはクォークと反対の符号の量子数を持つ。クォークはスピン-1⁄2粒子、つまりフェルミ粒子である。
中間子は価クォーク-反クォークの対で構成されており、バリオン数は0となる。一方、バリオンは三つのクォークで構成されており、バリオン数は1となる。この記事の具体例では、アップ、ダウンおよびストレンジフレーバーのクォークモデル(これは近似的にSU(3)対称性を形成する)について議論する。フレーバーの数をさらに増やす一般化も存在する。

https://ja.wikipedia.org/wiki/クォークモデル
y|
|p
____|____
/\ | /\
q/U+\ | /V+\q
/ \ | / \
__/Tー____\|/____T+\_→
\ /|\ / t
\ / | \ /
p \Vー/ | \Uー/ p
\/___|___\/
|q
SU(3)の図
https://ja.wikipedia.org/wiki/特殊ユニタリ群
n次の特殊ユニタリ群(とくしゅユニタリぐん、英語: special unitary group)SU(n) とは、行列式が1のn次ユニタリ行列の為す群の事である。群の演算は行列の積で与えられる。
特殊ユニタリ群 SU(n) はユニタリ群 U(n) の部分群であり、さらに一般線型群 GL(n,C)の部分群である。
特殊ユニタリ群は素粒子物理学において、電弱相互作用のワインバーグ=サラム理論や強い相互作用の量子色力学、あるいはそれらを統合した標準模型や大統一理論などに出てくる。
 の生成子 T の基本表現は
の生成子 T の基本表現は
 はゲル-マン行列である。
はゲル-マン行列である。
____|____
/\ | /\
/ \ | / \
/ \ | / \
__/______\|/______\__
\ /|\ /
\ / | \ /
\ / | \ /
\/___|___\/
|
____|____
/ | \
/ | \
/ | \
__/_______|_______\__
\ | /
\ | /
\ | /
\____|____/
|
以下転載:
http://sci.tea-nifty.com/blog/2015/12/nhk124-8ed5.html
調和解析については第三回
以下転載:
http://sci.tea-nifty.com/blog/2015/11/nhk-1127-41d4.html
と
数学
y|
|p
____|____
/\ | /\
q/U+\ | /V+\q
/ \ | / \
/ \|/ \
ーー〈Tー ーーーーーXーーーーー T+〉ーー→
\ /|\ / t
\ / | \ /
p \Vー/ | \Uー/ p
\/___|___\/
|q
:SU(3)の図
奇妙な一致。
Y
中性子 n0____|____P+ 陽子
/\ |1 /\
/ \ | / \
/ \ | / \
__/______\|/______\__
Σ ー \ー1/2 Σ 0|\λ0 ー1/2/Σ+
ー1 \ / | \ / 1
\ / | \ /
\/___|___\/
三ー |ー1 三0
クォークモデルは、1950年代から1960年代に渡って発見された非常に多くのハドロンを系統立てて分類するために開発され、1960年代後半から現在までの実験によってその正しさが検証されている。これらの実験的証拠により、ハドロンは"基本粒子"ではなく、それを構成する"価クォーク"が基本粒子であると考えられている。クォークモデルは価クォーク単位でハドロンを分類する。価クォークとは、ハドロンの量子数の実体を担っているクォークおよび反クォークである。
これらの量子数はハドロンの種類を同定するためのラベルであり、二種類に分けることができる。一つは、ポアンカレ対称性を持つJPCである。ここで、J、PおよびCはそれぞれ全角運動量、パリティ対称性およびチャージ対称性である。二つ目は、アイソスピン、ストレンジネスおよびチャームなどのフレーバー量子数である。クォークモデルは八道説の分類法に従っている。(#中間子および#バリオン参照)
全てのクォークにはバリオン数1⁄3が割り当てられている。アップ、チャームおよびトップクォークは電荷+2⁄3を持ち、ダウン、ストレンジおよびボトムクォークは電荷−1⁄3を持つ。また、反クォークはクォークと反対の符号の量子数を持つ。クォークはスピン-1⁄2粒子、つまりフェルミ粒子である。
中間子は価クォーク-反クォークの対で構成されており、バリオン数は0となる。一方、バリオンは三つのクォークで構成されており、バリオン数は1となる。この記事の具体例では、アップ、ダウンおよびストレンジフレーバーのクォークモデル(これは近似的にSU(3)対称性を形成する)について議論する。フレーバーの数をさらに増やす一般化も存在する。

https://ja.wikipedia.org/wiki/クォークモデル
八道説(中央に二つ)
Eightfold Way (physics) - Wikipedia, the free encyclopedia
https://en.m.wikipedia.org/wiki/Eightfold_way_(physics)Flavour symmetry
Main article: Flavour (particle physics)
There is an abstract three-dimensional vector space:

and the laws of physics are approximately invariant under applying a determinant-1 unitary transformation to this space (sometimes called a flavour rotation):

Here, SU(3) refers to the Lie group of 3×3 unitary matrices with determinant 1 (Special unitary group). For example, the flavour rotation

is a transformation that simultaneously turns all the up quarks in the universe into down quarks and vice versa. More specifically, these flavour rotations are exact symmetries if youonly look at strong force interactions, but they are not truly exact symmetries of the universe because the three quarks have different masses and different electroweak interactions.
This approximate symmetry is called flavour symmetry, or more specifically flavour SU(3) symmetry.
(This is a slightly over-simplified description of flavour rotations, ignoring anti-quarks etc.)
Connection to representation theory



Main article: Particle physics and representation theory
Assume we have a certain particle—for example, a proton—in a quantum state  . If we apply one of the flavour rotations A to our particle, it enters a new quantum state which we can call
. If we apply one of the flavour rotations A to our particle, it enters a new quantum state which we can call 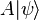 . Depending on A, this new state might be a proton, or a neutron, or a superposition of a proton and a neutron, or various other possibilities. The set of all possible quantum states spans a vector space.
. Depending on A, this new state might be a proton, or a neutron, or a superposition of a proton and a neutron, or various other possibilities. The set of all possible quantum states spans a vector space.
 . If we apply one of the flavour rotations A to our particle, it enters a new quantum state which we can call
. If we apply one of the flavour rotations A to our particle, it enters a new quantum state which we can call 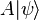 . Depending on A, this new state might be a proton, or a neutron, or a superposition of a proton and a neutron, or various other possibilities. The set of all possible quantum states spans a vector space.
. Depending on A, this new state might be a proton, or a neutron, or a superposition of a proton and a neutron, or various other possibilities. The set of all possible quantum states spans a vector space.
Representation theory is a mathematical theory that describes the situation where elements of a group (here, the flavour rotations A in the group SU(3)) are automorphisms of a vector space (here, the set of all possible quantum states that you get from flavour-rotating a proton). Therefore, by studying the representation theory of SU(3), we can learn the possibilities for what the vector space is and how it is affected by flavour symmetry.
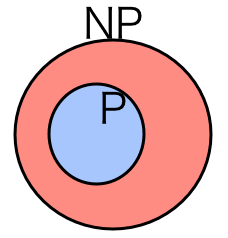
Since the flavour rotations A are approximate, not exact, symmetries, each orthogonal state in the vector space corresponds to a different particle species. In the example above, when a proton is transformed by every possible flavour rotation A, it turns out that it moves around an 8-dimensional vector space. Those 8 dimensions correspond to the 8 particles in the so-called "baryon octet" (proton, neutron, Σ+, Σ0, Σ−, Ξ−, Ξ0, Λ). This corresponds to an 8-dimensional ("octet") representation of the group SU(3). Since A is an approximate symmetry, all the particles in this octet have similar mass.
Incidentally, every Lie group has a corresponding Lie algebra, and each group representationof the Lie group can be mapped to a corresponding Lie algebra representation on the same vector space. The Lie algebra SU(3) can be written as the set of 3×3 traceless Hermitian matrices. Physicists generally discuss the representation theory of the Lie algebra SU(3) instead of the Lie group SU(3), since the former is simpler and the two are ultimately equivalent.
y|
|p
____|____
/\ | /\
q/U+\ | /V+\q
/ \ | / \
__/Tー____\|/____T+\_→
\ /|\ / t
\ / | \ /
p \Vー/ | \Uー/ p
\/___|___\/
|q
SU(3)の図
https://ja.wikipedia.org/wiki/特殊ユニタリ群
n次の特殊ユニタリ群(とくしゅユニタリぐん、英語: special unitary group)SU(n) とは、行列式が1のn次ユニタリ行列の為す群の事である。群の演算は行列の積で与えられる。
特殊ユニタリ群 SU(n) はユニタリ群 U(n) の部分群であり、さらに一般線型群 GL(n,C)の部分群である。
特殊ユニタリ群は素粒子物理学において、電弱相互作用のワインバーグ=サラム理論や強い相互作用の量子色力学、あるいはそれらを統合した標準模型や大統一理論などに出てくる。
SU(3)
 の生成子 T の基本表現は
の生成子 T の基本表現は はゲル-マン行列である。
はゲル-マン行列である。____|____
/\ | /\
/ \ | / \
/ \ | / \
__/______\|/______\__
\ /|\ /
\ / | \ /
\ / | \ /
\/___|___\/
|
____|____
/ | \
/ | \
/ | \
__/_______|_______\__
\ | /
\ | /
\ | /
\____|____/
|
以下転載:
http://sci.tea-nifty.com/blog/2015/12/nhk124-8ed5.html
2015年12月 4日 (金)
NHK 数学ミステリー白熱教室~ラングランズ・プログラムへの招待~12/4の第四回(最終回)「数学と物理学 驚異のつながり」を見た。
このシリーズも今夜で最終回。 では今日も速記メモで。
---
透明な壁にP=NP?*とナビエ・ストークス方程式**が書いてあるのが楽しいいつもの紹介からスタート。
さて今日登場するフレンケルさんはやはり半袖の黒シャツ。
数学の異なる分野の間の隠された関係について話してきた。まとめてみよう。
ジグソーパズルを思い出してほしい。数学には異なる分野がある。
これまでに登場したのはまず数論、数の研究だ。
そして調和解析、楽器からの波やモジュラー形式などを紹介した。
それから幾何学についても話した。対称性を見た。
ロバートラングランズによって提唱されたラングランズプログラム。異なる分野を統一しようとする試みだ。この一連の予想は50年の間に拡張されてきた。
今回特に話をしたいのは、量子物理学とのつながりだ。
数学とは全く異なる、物理学の世界ともつながりがありうる。
それが、この10年の間に明らかになった最先端の研究だ。10年前に講義をしたらこれは取り上げられなかった。
さて、まずは、、、、
対称性について思い出してみよう。
対称性は一連の講義をつなぐ秘密の鍵だった。
最初は雪の結晶やボトルの回転などを議論した。幾何学の話だ。
数論における対称性についても話をした。ガロア群の話だ。
調和解析の対称性についても、志村・谷山・ヴェイユ予想について話した。
では量子物理学においてどのように対称性が現れる?
まず、対称性の概念がどのような役割を演じるか見てみよう。
原子からすべての物質ができていることをしっているね?そして原子核と電子も。
原子核は陽子と中性子からなることも知っているね?
炭素原子は陽子6個、中性子6個、電子6個だ。
陽子と中性子はさらに小さな粒子に分けられることが分かっている。
素粒子を見つけるには洗練されたマシンを使うことが重要だ。大型ハドロン衝突型加速器。国境をまたぐほど巨大なもの。スイスのジュネーブにある。
この100億ドルもする機械はある発見をもたらした。
ヒッグス粒子だ。標準理論に重要なものだ。
でも1960年代に時計の針を戻そう。
当時は小さな加速器を使っていた。バークレーの研究所でも素粒子だと考えられるものが次々見つかった。
しかし困った状況になった。あまりにたくさんの素粒子が存在したからだ。
一体誰がこんなにたくさんの粒子を注文したんだ、といった人もいた。(これはRabiさんです)
ところが数学の群を使って説明することができたのだ。
その理論の発展にマレー・ゲルマンが貢献した。
SU(3)という群を使ってハドロンの分類を行い、クォークの存在を
アップ・ダウン・ストレンジというものがあることを理論で示した。
クォークは整数ではなく、分数の電荷をもつ。これまで一度も観測されていないためありえないとも考えられた。
現在、陽子と中性子は3つのクォークから成り立っていることが分かっている。
アップクォークとダウンクォークを含んでいる。
SU(3)という群が重要だ。解説しよう。
我々は非常に重要な群を知っている。球の表面の回転の群だ。
バスケットボールを持ってきて、ある軸を選んで回転させる。
SO(3)という名前だ。
3次の特殊直交群。
SU(3)は特殊ユニタリー群。
我々の住んでいる3次元と複素数の違いだ。
複素数は2乗するとマイナス1になる数を含んでいる。
実は、数学者でさえも複素数を理解するのに何世紀もかかった。カルダーノという数学者は複素数のことを精神的拷問と呼んだ。
SU(3)は複素数を使った群だ。
球の回転と似ている。でもどうしてハドロンと関係する?
粒子がグループに分類できるということに物理学者が気づいた。
8個のグループを作れる。陽子、中性子とあと6個。
数学の本に載っている図と同じだとゲルマンが思った。ウエイトダイアグラムだ。
ゲルマンは同僚に見せてもらった図を見て、これはつながりがあると。
まるで探偵がやるような仕事だ。手がかりを見つけ犯人を逮捕する。
でも数学者は全く関係ないところでこの図を見つけていたのだ。
チェンニン・ヤンの言葉を紹介したい。
”これほどミステリアスで畏敬の念を起こさせる事実がほかにあるだろうか。物理世界の構造が論理と形式の美しさをもとに作り出された数学的概念と緊密に結びついているのだ”
ところでSU(3)からどのようにクォークが見つかったのか?3から3つのクォークが見つけられた。さらにあと3つの
アップ、ダウン、ストレンジ、チャーム、トップ、ボトムを加えて6つになる。
名前の由来は聞かないで、、、
ラングランズプログラムとのつながりは何だろうか?
標準理論について話そう。
様々なものがこれに基づいて見つかっている。
さて、自然界の力には
重力、電磁気力、弱い力、強い力
がある。
すべてのものを記述する式があったらつまらないと思う?
いや、たった一つの式で表すことはできないだろう。でも近づくことはできる。地平線のようなものだ。でも私は一つの式で表されるとは思っていない。あるエネルギー領域ならある。
でも別の領域では説明できない。
スーパーストリング理論もそうだ。私の仕事でもある。
まだ実験で実証されていないし、物理学と数学がせめぎあっている。
さて、標準理論が重要だと考えているのは、それがゲージ理論だからだ。
対称性の群に基づいて力の性質を説明する。
例えば電磁気力はU(1)という群を使っている。みんなが知っている群だ。
円だ。
弱い力はSU(2)、強い力はSU(3)。
電磁双対性について注目してほしい。
異なるゲージ理論の間につながりがある。
19世紀のマックスウェルにさかのぼる。マックスウェル方程式だ。
偏微分方程式だがエレガントでシンプルに見える。
電場と磁場の間に対称性が存在する。E→B、B→-E
ボルシチのレシピを使って説明した。
材料の交換を意味する。
ジャガイモ5つと玉ねぎ5つと書いてあったら材料を交換しても変わらない。
個数が違ったら味が変わる。。。
では他のゲージ理論にも電磁気力のような双対性があるのか?
電磁気力はEとBを交換しても方程式は変わらなかった。
ある群のゲージ理論は別のゲージ理論になる。
それが、ラングランズ双対群と呼ばれるものだった。
それでラングランズプログラムとゲージ理論につながりがあると考えられた。
一方にある群があって、他方に対応する別の群がある。
U(1)の双対群はU(1)だから電磁気力は変わらない。
SU(2)、SU(3)は双対群は同じにはならない。ここで詳しく説明することは骨が折れる、、、ので実演する。
美しいショーだと思うよ。
コップのトリックと呼ばれるものだ。
まずコップを掌に載せて、種も仕掛けもございません。
腕をねじってコップを360°回転させる。さらに回転させると腕がもっとねじれて病院送りになると思うでしょ??
いや元に戻った。
SO(3)の双対群はSU(2)になるんだ。コップトリックはそれをうまく表している。
SO(3)は空間の回転なので360°回すと、さらにSU(2)は720°回転させると元に戻る。
電磁気学のような双対性がU(1)以外にも存在すると予測されている。
SO(3)の双対はSU(2)のゲージ理論になる。
なぜ物理学にラングランズ双対群が現れるのか?
80年代になって認識された。70年代の終わりに複数の物理学者が研究していた。
ラングランズの業績については知らなかったがラングランズ双対群を研究していた。
その後25年間、答えが得られなかった。しかしフランケルさんもこの発見に関与した。
数学と物理学がつながっているのだ。
つながりとは?
2004年に決定的な出来事があった。
プリンストン高等研究所が舞台だ。
ある会議が開かれた。オーガナイザーの一人としてフレンケルさんも加わった。
数学者と物理学者が集まり、ひらめいたことを話し合った。
アプローチは本当の探偵のようなものだ。
物理学者であり、数学でも大きな功績があるエドワード・ウィッテンもオーガナイザーだった。
京都賞も受賞した。
彼はあるアイデアがある。それについて話をしよう、と3日目に行った。
ビデオや音声はないが、ノートは取ってある。彼は正しかった。
そして最初の論文を書いた。学会誌の丸々一冊になるほど長い論文。
そしてフレンケルさんを含む研究者たちが発展させた。
マトリョーシカのようなものだ。中を開けるとまた中に入っていて、、、という。
ヒントを示そうと思う。
3次方程式、y^2+y=x^3-x^2、素数pを法とする三次方程式の解の個数を数えよ、
というものを前回示した。
実数でも解を、複素数でも解を求めることができる。
同じ方程式の解を複素数でも求めることができる、というのが重要。
pを法とする場合はある調和解析の関数となるが、
複素数の場合は、ある幾何学の図形になる。それはトーラス。
それは分かれ道のようなものだ。
素数を法をしたら数論となり、複素数なら幾何学になる。
これこそがつながりだ。
幾何学もこのようにしてラングランズプログラムに含まれる。
ウィッテンと共同研究者がやったことは何か?
まずは数論から幾何学へ、次に幾何学から量子物理学へ、という2ステップで繋げた。
チェンニンヤンの言葉はすでに紹介した。
数学が現実世界とつながっている素晴らしいものだということ。
しかし数学でU(1)、SU(2)、SU(3)だけではない。どの群でも意味がある。物理学では自然界において見つけられるものだけが興味の対象になる。
数学と物理学にはすでに違いが存在する。これが一つ目の違い。
次に、数学の理論が物理学の発展に先立って行われたが、それが何かに関係するとは思われなかった。
数学者がどのように見つけたかは説明できるが、、、
でも数学を発見したのか、発明したのか?
ガロアの発見や志村・谷山・ヴェイユ予想は人類の金字塔というだけでなく、人類の高い志の賜物と言える。
数学についてよい話がある。
数学で生まれた偉業のすべてが我々の手から奪われることはない、というものだ。
最高裁がある判決を出した。数式で特許を取ることはできない。
E=mc^2で特許は取れない。
数学を共有することができ、それを奪うことはできない。研究をやめさせることはできない。
講義の終わりが近づいてきた。
最後に伝えたい言葉がある。
アイザック・ニュートンの言葉だ。
私は浜辺で遊ぶ子供のようだった。浜辺ですべすべした小石や美しい貝殻を拾って喜んでいた。
しかし私の目の前には真理の大海原が発見されることなく広がっていたのだ。
すばらしい生徒であってくれてありがとう。楽しい講義だった。
---
(これまでのおさらいはこちら)
第一回目はこちら。
第二回目はこちら:
第三回目はこちら。
---調和解析については第三回
以下転載:
http://sci.tea-nifty.com/blog/2015/11/nhk-1127-41d4.html
2015年11月28日 (土)
NHK 数学ミステリー白熱教室~ラングランズ・プログラムへの招待~ 11/27の第3回 “フェルマーの最終定理”への道 ~調和解析の対称性~を見た。
第一回、第二回はこちら↓
では第三回の速記メモ、谷山豊についても話そう、とのことです。
今回も半袖シャツ(黒)で現れたフレンケルさん。
まずはここまでのおさらい。
ラングランズプログラムは異なる数学の分野をつなげ、統一しようという試み。
ラングランズが最初のアイデアを出したのは1960年後半。その後、数学の他の分野にも広がった。
まずはこの文書を観てほしい。ロバート・ラングランズがアンドレ・ヴェイユに送った手紙。。。についていたメモ。
彼のアイデアが示されている。1967年に書かれたもの。
これはプリンストン高等研究所の資料室に保管されている。
内容は、
ヴェイユ教授
講演のお招きを受け同封の手紙を書きました。
書き終えてから
私は確信を持てることがほとんどなにもないことに気づきました。
これを純然たる推測としてお読みいただけるならありがたく存じます。
そうでなければお手近にくずかごがあると思います。
---
だが、捨てられるどころか、この手紙はその後、数学の全く新しい予想を生み出した。
これから話すのはラングランズプログラムに直接関係している。
フェルマーの最終定理だ。
x^n + y^n = z^n
nは固定された整数、3,4,5,...
x,y,zがこの方程式の未知数となる。
おおよそではなく、ぴったり等しくなければいけない。
フェルマーの最終定理は、この正の整数x,y,zが存在しない、ということを表している。
ところでなぜnは3や4?2でもいいんじゃないか?
n=2のときを考えてみよう。
x^2+y^2=z^2
になる。これに見覚えはない?
最初の講義で紹介した、ピタゴラスの定理に出てくる式。直角三角形の。
ではこの式について考えてみよう。
x,y,zは存在するだろうか?
ピタゴラス数と呼ばれる数がそれにあたる。
1つ目はx=3,y=4,z=5だ。
5,12,13もそう。
これが書かれたディオファントスが書いた算術という本をフェルマーが読んでいたとき、
この式でn=2より大きいときはどうなるだろうか、と思った。
これが数学を発展させるやり方。
フェルマーはその本の余白に有名な、
”私は真に驚くべき証明を見出したが、余白が狭すぎるので書くことはできない”
と書いた。
君たち、テストで同じことをしたらだめだよ!とギャグを飛ばして笑いを取るフレンケルさん。
でもなかなかうまい手だ。その後、フェルマーは何も残していない。
n=4の証明はしたんだが、それ以外はない。
1995年に証明されたのだが、350年もかかったことになる。
しかもそれはフェルマーの最終定理を直接証明したのではなく、
志村・谷山・ヴェイユ予想を証明したのだ。
志村・谷山・ヴェイユ予想を証明すればフェルマーの最終定理を証明することになる。
実はそのことに最初に気づいたのは、1986年、フレンケルさんの同僚のケン・リベットさんだった。
カフェストラーダでコーヒーを飲んでいたときアイデアが出たそうだ。
すでにこのとき志村・谷山・ヴェイユ予想は有名だった。
最終的に、
アンドリュー・ワイルズとリチャード・テイラーが1995年に志村・谷山・ヴェイユ予想を証明した。
ここで予想とはどういうことをいうのか説明する。
どうやら真実とは思われるがはっきりとはわからない、証明がないもの。
フェルマーのは本当は予想だった。
志村・谷山・ヴェイユの場合は予想と呼ばれていた。
ラングランズプログラムも同様だ。いくつもの予想で構成されている。
なぜ、志村・谷山・ヴェイユ予想について話しているかというと、ラングランズプログラムの特殊なケースに当たるから。
---
ここで数学の概念を紹介しよう。
時計算術だ。
この目覚まし時計の電源をいれよう。
君たちを起こすためじゃないよ(とまたギャグ)
アナログ時計が良かったんだがデジタル。
最近はアナログの目覚まし時計、売ってないんだねー(そうそう、私も買いに行ったときにないことはなかったが少なくて仕方なくデジタルにした)
時計は10:00を指している。
5時間働くと?
3時になった。どうしてこうなるの?
単に足したら
10 + 5 = 15
じゃないの?
時計は1時から12時しかない。
そこで10+5=3になる。
どうなってるの?12を引いた数になる。
13は1に、14は2に、、、、
これが時計算術。
モジュロ演算とも呼ぶ。
15 = 3 (modulo 12)
12を法として15は3に等しい。
と呼ぶ。
足し算も掛け算もできる。
ところで12である必要はない。別の正の整数でもいい。
数学で最も面白い時計は素数の場合だ。
ここで最も重要な概念がでたぞ。素数だ。
素数に触れずにどうやって数論を語れるか。。。
素数とは何かを思い出すと、
1と自分自身以外で割り切れない正の整数だ。
ちなみ1は慣例として含めない。
最初の素数は2、次が3、5、7、
ここで私は9と書いて君たちが起きているかいつも試すんだが、、、今日は起きているようだからやめておこう(笑)
次は11。
偶数なのは2だけだ。
素数は数の原子のようなものだ。
すべての整数は素数から作ることができるから。
60=2^2*3*5
など。
時計に戻る。
例えば7時間時計を考える。0,1,2,,,,6と目盛りが。
解を見つけるといってもどの範囲で見つけるかが重要。
例えばフェルマーの最終定理は正の整数の範囲で。
でも違う範囲なら、例えば
y^2 = x^3 - 3*x + 5
という三次方程式の解が求まるかもしれない。
この方程式では正の整数全体から探しているのではなくて、
素数pを法とする解を求めようとしている。
ということは必ずしも右辺と左辺が等しくなくていい。pの整数倍だけ変わっていてもいい。
つまり、様々な3次方程式が素数pを法とする解を持つか?
そして解の個数はいくつか?
これが志村・谷山・ヴェイユ予想に出てくる。
あらゆる時間の時計が必要になる。素数は無限にあるので、
1つの方程式に対して無限回の計算をしないといけない、、、
志村・谷山・ヴェイユ予想ではそういう問題を考える。
例えばp=5の時。
y^2 + y = x^3 - x^2 modulo 5
を考える。
x=0,1,2,3,4を考えよう。yも同じ。
これらを入れてみたら?
25通りあるので手計算でも計算できる。
4つの解がある。
x=0,y=0
x=0,y=4 (20=0 modulo 5)
x=1,y=0
x=1,y=4
だ。
一つ一つの素数ごとに解の個数を確かめる。
表にまとめると?
素数p:2,3,5,7,11,13
解の個数S(p): 4,4,4,9,10,9
p-S(p) : -2, -1, 1, -2, 1, 4
最後のは素数から解の個数を引いたもの。
素数の値が大きくなると計算が膨大になる。
規則性はある?
一見するとないように見えるが、、、
奇跡が起きた。ランダムじゃない。
p-S(p)は調和解析に登場する、たった1行の数式で知ることができる。
もう一度言おう。
p-S(p)は調和解析に登場する、たった1行の数式で知ることができる。
だから私はこれを奇跡と呼びたい。
その数式とは、
q*(1-q)^2*(1-q^11)^2*(1-q^2)^2*(1-q^22)^2*(1-q^3)^2*(1-q^33)^2*(1-q^4)^2*(1-q^44)^2*・・・
だ。
この式はどのように作られている?
いくつかの単純な数式を組み合わせたもの。
まずはq。ただの変数だ。
次に
q*(1-q)^2*(1-q^2)^2*(1-q^3)^2
を考える。さらに11の倍数の式を掛ける。
*(1-q^22)^2*(1-q^22)^2*(1-q^33)^2
さて、この式の括弧を外して展開するとどうなるか?
=1-2q^2-1q^3+2q^4+1q^5+2^q^6-2q^7-2q^9-2q^10+1q^11-2q^12+4q^13・・・
係数を
b1, b2, b3・・・などと書く。
b1=1, b2=-2, b3=-1, b4=2
そして、この係数こそが探している数。b(n)と書いたほうがわかりやすいかな?
これを使うと、、、
p-S(p) = b(p)
となるのだ。
これが志村・谷山・ヴェイユ予想が我々に教えてくれることの一例だ。
ラングランズはこれを
「混沌の中に秩序を見いだす」
といった。
複雑だった問題に、いわばソースコードのようなものを発見したんだ。
解の個数を求めるDNAを見つけたようなもの。
さて、ここまで対称性が大きな役割を果たす、と言った。
調和解析における対称性とは?
さっきの数式は関数として捉えることもできる。
特別な変換をしても変化しない。
先ほどの形式はモジュラー形式とも呼ばれ、
単位円と呼ばれる領域で定義された関数で、非常に美しい対称性を持つ。
その一例が、
f(q) = q*(1-q)^2*(1-q^11)^2*(1-q^2)^2*(1-q^22)^2*(1-q^3)^2*(1-q^33)^2*(1-q^4)^2*(1-q^44)^2*・・・
まるで魔法のようなことが起きる。
数論の分野の問題は、調和解析という別の数学の分野で解くことができるのだ。
ではなぜモジュラー形式は調和解析ということができるのか?
最初の講義で、調和解析は三角関数で表される音に関するものだと言ったが、
重要なのは2πずらしても変化しないという対称性を持つことだった。
モジュラー形式も単位円上で定義された関数で、三角関数と似た対称性を持つ。
まとめると、
ある数論の問題
y^2 + y = x^3 - x^2
素数pを法とする三次方程式の解の個数を数えよ
というものがあり、一方では
ある調和解析の関数、単位円上で定義されたf(q)がある。
その関数は特殊な性質(対称性)を持っている。
で、志村・谷山・ヴェイユ予想とは、
あらゆる三次方程式の解を数える数論の問題に対し
その答えを導く調和関数のモジュラー形式が存在する
というもの。
なぜつながっているのか?正直なところ理由はわかっていない。
ワイルズとテイラーが証明したのだが、隠された理由があるのかもしれない。
世界の7不思議のようなものだ。どこにも出かけていく必要がないのに見つけられる。
では、志村・谷山・ヴェイユ予想にかかわった人々について話そう。
まずは
谷山豊。
1958年に亡くなった。この予想のアイデアを最初に発表したのは1955年、戦後の日本で初めて開催された数学の国際会議。
東京と日光で開かれた数論の会議で、この予想を出した。
その予想は同僚の志村五郎とアンドレ・ヴェイユによってさらに研究されることとなった。
どうしたらこんな革命的な発見ができたのか?
不思議にずっと思っていた。
谷山には深い洞察力があった。
数学の洞察とは何か?
今ではコンピュータが人間に追いついたと言われることがある。でも意義を唱えたい。
直感力が大事で、このような発見を行うとき、普通とは違うなにか別な力が働く。
谷山の話には悲しい続きがある。
予想を出してからしばらくして谷山は自ら命を絶った。
遺書にはこうかかれている
”ただ気分的に言えるのは将来に対する自信を失ってしまった。
私の行為がある種の裏切りであることは否定できませんが
最後のわがままと捉えてください。
私がこれまでの人生で行ってきたように”
彼の死からほどなく、婚約者も命を絶った、、、
”私たちは決して離れないと約束しました。だから私も一緒に行かなければなりません”と書置きを残して、、、
このことは悲劇だが、数学者も人間であり、あらゆる経験をし、様々な感情を持っていることを気づかせる。
そして死後、同僚の志村が谷山をたたえている。
”彼が生きていた時よりも今のほうがずっと強く彼の高潔な寛大さを感じる。
それなのに彼が切に支えを必要としていたとき誰も彼の支えとなれなかった
このことを思うと、私は深い悲しみに打ちのめされる”
と。
これは数学の物語であり、人生の物語でもあった。
次回は量子物理学について話そう。物理学における対称性について、そしてそこにラングランズプログラムがどのように現れるか?
第四回目(最終回)はこちら
2015年11月21日 (土)
NHK 数学ミステリー白熱教室~ラングランズ・プログラムへの招待~ 11/20の第2回「数の世界に隠された美しさ ~数論の対称性~」を見た。
第一回目の速記メモはこちら:
では今回も速記メモで:
最初の3分くらいは第一回目と同じ、フレンケル先生の紹介と講義のあらすじ。
第二回では、数論に焦点を当てる。対称性が数や方程式に対する我々の認識を変えたことを示そう。ガロアの革新的発見も。
ではフレンケル先生が半袖の軽装で登場。やはりイケメン。
前回のおさらいをしよう。強調したのは複数の異なる分野が数学にあり、ジグソーパズルに数学の研究は似ているということ。
数論、調和解析、幾何学に焦点を当てる。
ロバートラングランズの写真を見せる。彼は50年前、別の数学者にあてた手紙でそのアイデアを書いた。
興味深い話は、彼は数か国語を流暢に操る。外国語で何冊も本を書いている。フランス語、ドイツ語、ロシア語、、、大学に入るまでは英語しか話せなかった。
フレンケルさんとはロシア語でやり取りしたいと言ってきた。で彼からロシア語の本で読んだリストを送ってきたが、フレンケルさんはそこまで読んでないかも、と恥ずかしくなった。
対称性については、前回ペットボトルやミカンで幾何学については学んだ。
今回は数論だ。
まずは数について、、、
整数とはどんな数?数えることで理解できる数。
0やマイナスの数などもある。
0の存在は神秘的で、その意味を理解するのに何千年もかかった。
私の電話番号は整数、生年月日も、ATMの暗証番号も、、、将来の技術革新で変わるかもしれないが。
分数という数もある。整数どおしの比を表している。
お金がそうだ。2.95ドルは2と95/100
古代は現実にあるのは有理数しかない、と思っていた。
しかしそれには無理がある。有理数ではない数に出会ってしまうからだ。
2辺が1の直角三角形の斜辺は?
1^2 + 1^2 = c^2
だからc^2=2.
ここでルートという記号を導入しよう。二乗すると2になる数、√2.
これが有理数で表せないことは簡単に証明できる。
こういうのを無理数といい、分数で扱うことのできない数。
さて、無理数と出会ったことで有理数の世界が崩れた。
数学ではすべてを受け入れた。逃げ出したり、そんなものは存在しないということなく、広い心で受け入れた。見知らぬ他人を受け入れるようなもの。
√2には親戚のような数がある。
2√2や3√2.
数を増やすことはよくやることだ。
√2/2とか。
これはまとめて表現できる。
p/q√2 (pとqは整数)
これですべて?そうではない。
m/nは有理数。
√2の親戚は分数で表せる?いやできない。
m/n=p/q√2と書くと
mq/np=√2となって
有理数で表されるので矛盾。
数を取り扱うときに重要なことは?演算だ。足し算、掛け算、割り算、引き算。
演算ができるかどうかが家族に入るかどうかということ。
有理数どおしの演算では有理数が出る。
重要なことは我々はこれが当然と思っている。
でも整数は違う。割り算では整数にならない場合がある。
足し算と掛け算では閉じているが、割り算では閉じていない。
有理数はすべての演算で閉じている。
無理数を含んで、どうしたら演算で閉じる新しい家族を作り出せる?
家族の形を数式で表すと、
a+b√2
となる。
でフレンケルさんが計算例を間違える(笑)。あ、もちろんすぐ訂正。
この新しい数の素晴らしいところが、
有理数に対するのと同じ演算ができるということ。
これを数体とよぶ。
√3などの別の無理数でもできる。
この新しい数の対称性とは???
(ピカチュウのTシャツを着た学生が映る)
a+b√2をa-b√2に変える。
この変換をしても体系は変化しない。演算で閉じている。
でまた6を36に書き間違える。今日は36が好きだなあ、黒板に間違った話を書くのは悪くない、誰が聞いているかわかるから。というフレンケルさん。
で2回変換すると元に戻る。
√2と-√2を考えよう。入れ替えても変化しない。
なぜ?
ピタゴラスの定理で嘘をついたことを謝る。
c^2=2のときc=√2といった。長さはプラスだから。でも-√2も答えだ。
同じ方程式を満たすので、蝶の2つの羽のような対称性を持つ。
x^2=2の答えは±√2だ。
2つとも同じ方程式から生まれた答えなんだ。
解の方程式を探すことと関係している。多項方程式や代数方程式と呼ばれている。
2次方程式は係数が整数の方程式なのに、答えは有理数じゃない。こうして体系が生まれた。
ここからガロア群と呼ばれる群のお話し。
フランスのエヴァリスト・ガロアは20歳で決闘で殺された。
死の前日に、数学の原稿を完成させていた。ある理論を急いで書き残したのだ。
もう時間がない、と原稿には書かれていた。
この20歳の男についてよく考える。明日殺されるとわかっていたのだろう。
ロウソクの明かりの下で、愛する人にではなく、自分の数学の発見を書いた。
同時代の数学者と共有したかった。
共有しなければなんの価値もないからだ。共有したときに初めて、愛のように価値が生まれる。一種のラブレターだと思う。我々全員にあてた、、、
数学の勉強が感動的であるのは、新発見をしたとき、新しい概念を生み出したとき、世界中の誰も知らないことを知ったとき、、、
ガロアが解決した問題とは?
ラジカル(累乗根)を使った解の公式の問題だ。バークレーでよく聞く過激という言葉じゃない(お、またジョークを挟んできた)。
そういやルートも別の意味をもっている。根っこという。
n√a
という累乗根の表し方をする。
累乗根だけで方程式の答えを書けるか?
x^2=2はもちろんかける。
2次方程式の解の公式は覚えているかな?
ax^2+bx+c=0
ちゃんとかけるかな、、、
x=(-b±√(b^2-4ac)/2a
累乗根だけが出てきている。
問題は2次より高い方程式に対してこれが作れるか?
3次方程式は?
ax^3+bx^2+cx+d=0
解の公式はある?あるとわかっている。ここから素晴らしい物語が始まる。
2次方程式の解はアル・フワーリズミの著作に示されていた。8世紀~9世紀の数学者。
1200年ほども前だ。
ソビエトでは切手が発行された。
本のタイトルに含まれる入れ替え、に関係するアルジャブルというアラビア語。ここから代数学の語源になった。
アルゴリズミと間違って発音された彼の名前もアルゴリズムの語源になった。
3次方程式が見つかるまでにはそこから700年。
ここで黒板には特殊な場合、x^3+px+q=0の解が示された。
これは累乗根を含んでいる。カルダーノの公式。
これは大スキャンダルだった。この公式はイタリアのデル・フェッロが発見した。当時の数学者は競争相手があるので発表しなかった。勝負で勝つためだ。相手にこれを解け、といって解けなかったら負け。
こういうのも案外いい方法かもしれない、と笑うフレンケルさん。
タルタリアも解の公式を得ていた。
タルタリアは秘密の公式をカルダーノに漏らした。話がうまいペテン師。誰にも言わないという約束で、、、
4年は約束を守ったが、デル・フェッロに見せてもらった。
タルタリアのは公表しないが、デル・フェッロのを公表すると、、、
アルス・マグナという本を書いた。代数の根本という副題。
タルタリアは激怒。残りの人生を私が発見したといってまわることに費やした。
そしてそのカルダーノの弟子、フェラーリ。
4次方程式の解の公式を発見した。
そしてそのフェラーリがタルタリアを破滅させる。カルダーノとの勝負を望んだが、弟子のフェラーリとタルタリアが勝負したのだ。
フェラーリの圧勝だった。タルタリアは職を失った。
では、、、
5次方程式に解の公式はあるのか?
6次以上でも、、、
しかし300年もの間解けなかった。最終的にガロアがそのような公式が存在しないと証明した。
たまたま4次までは存在した。ラッキーだった。
ではどのように証明した?
ガロアは真正面から解かずに、ハッキングした。
5次方程式 ax^5+...=0
解の公式を見つけようとしたのではなく、問題を読み替えた。
あなた方はやり方を間違っている。方程式の答えを探そうとしているがそうではなく問うべきことは
”方程式の解の対称性とは何か?”
ということだ。
解の対称性は解を知らなくてもわかる。
x^2=2の解、√2と-√2の二通りあるが、これを入れ替えても同じ。
ガロア群は2つの物体の入れ替えに等しい。
3次方程式は3つの物体の入れ替えの群、4次方程式は
4つの物体の入れ替えの群。
ガロアのひらめきは、方程式の解の公式を累乗根で書けるか?というのは方程式の群の構造を調べればわかる、というもの。
入れ替えの群がその特性を持つかに等しい。
2個、3個、4個の入れ替えには存在するが、5個以上では存在しない。
問題をハッキングしたことで300年間わからなかったことを明らかにした。
ところで、学校では数学の授業であの公式を覚えなさい、この公式を覚えなさいと言われる。方程式の解の公式もそんなものの一つ。学生はガロアの功績をありがたいと思うだろう。たくさんの公式を覚えなくていいから。
しかし数学とは公式と計算を覚えるだけではない。概念と考え方を学ぶものだ。
ガロア群がいい例になっている。
では最終的にはどのようにやったか?
5つの物体の入れ替えの群。
ちなみにn次方程式はn個の解を持つことはわかっている。何通り入れ替え方がある?
n個の場合はn(n-1)...2*1=n!
なので5個なら120通り。
2次、3次、4次はそれぞれ2、6、24通りで構造が単純で、可解と呼ばれる。
しかし5次では120通りではるかに複雑になり可解じゃなくなる。
入れ替えは数学では対称群とも呼ばれている。
質問が出た。
解の公式があるときとないときの違いを詳しく知りたい。
説明しよう。
可解である群とはどういうものか?
それは可換か非可換か、ということと関係している。
可換とは順番を入れ替えても結果は同じ、非可換は入れ替えたら変わる。
ペットボトルの回転は可換。球の場合は違う。軸が違うもので回転させると結果が異なる。
可解である群は可換群で構成される。
可解でない群は可換群では構成されない。
ここまでをまとめる。
前回は幾何学の対称性を、今回は数論での対称性を見た。
入れ替えの群だ。方程式の解の公式が存在するのかどうか。
次回は、ラングランズが数論の問題をどのようにして調和解析に結びつけたのかについて。
(ラングランズの新聞に載った写真を見る。ガロア理論と書かれている。)
そしてフェルマーの定理についてみてみる。
2015年11月14日 (土)
NHK 数学ミステリー白熱教室~ラングランズ・プログラムへの招待~ 11/13の第1回「数学を“統一”する!」を見た。
エドワード・フレンケルさんが講義をするというので話題のシリーズ。
専門的な講義としては
なんかがありますが、これをどう素人向けに解説してくれるのか興味あるところ。
で第一回を録画したのをさっき見た。以下、速記メモ。長いよ。
---
カリフォルニア大学、バークレー校。
自由な校風で知られるこの大学に注目の研究者がいる。エドワード・フレンケル教授だ。
ラングランズ・プログラムに挑んでいる。数論、幾何学、解析学、など一見互いに無関係な分野が実はミステリアスなつながりがあることを証明しようとしている。
これが分かれば様々な数学の難問が解ける。
数学と物理学の間にも驚異のつながりがあると予想している。
さて、今回一般の学生から専門家までに向けた4回の講義を行うことになった。
おっとカップを手にもってぐるっとまわすというおなじみのあれをやっているぞ。
ガロア理論、フェルマーの定理、スーパーストリングまで登場予定とのこと。
あ、確かにイケメンだな。フレンケルさん。
数学の美しさや数学とは何か?について話すという。
第一回の今日は数学の大統一理論を紹介する。
こんにちは、みんな元気かい?
私はわくわくしている。みんなにもそうなってほしいね。
我々数学者は、数学がいかにエキサイティングかよく知っている。
このわくわくを共有したい。
君たちが思う数学と私の思う数学は、、、
ペンキ塗りとゴッホ作の”星月夜”のように違う。どちらも塗料をつかっているけど違う。
学校で教わる数学はペンキ塗りに似ていると。
数学はペンキ塗りじゃなくて偉大な画家の作品を楽しむのに近い。
ラングランズプログラムについて話したい。この50年で大発展を遂げた偉大な理論だ。
その前に、、、数学のことをもう少し紹介したい。
ガリレオ・ガリレイの言葉
「自然という書物は数学の言語で書かれている。その文字は三角形 円などの幾何学的な図形である。もし数学がなければ我々は自然をまったく理解できない 暗い迷宮を虚しく彷徨うようなものだ」
そう、確かに数学は自然を記述する。物理学の理論は常に書き換えられている。
ニュートンは重力の理論を作ったが、アインシュタインに書き換えられた。
もしかしたら君たちの誰かが書き換えるかも?
しかし数学の理論は物理と違う。
書き換えられることはない。永遠に。普遍なものだ。
ここでロシアのトルストイに触れる。もしトルストイが存在しなかったらアンナ・カレーニナなどの名作は存在しなかっただろう。
だが、数学は違う。ピタゴラスの定理。a^2+b^2=c^2.2500年前に誕生した定理だ。
でも、もしピタゴラスがいなかったら?別の誰かがこれを発見したはずだ。
実際に数多くの人が知っていたことが分かっている。
今でも子供が気づくかもしれない。。。
この定理が書き換えられることがある?a^2+b^2=c^3になる?そんなことはないだろ?
我々が生きている現実世界とは数学は違う、と考えている人もいる。
プラトンにまでさかのぼる考え方だ。
人間が作り出したものか?人間がいなくても普遍的なものか?はまだ答えはでていない。
もし、宇宙人に出会ったとする。あったことがある人もこの中にいるかも(笑、とちょっとギャグを飛ばして受けてる)。
彼らも同じ数学を持っているだろうか?
ケプラー186fなどの地球に似た惑星が発見され、知的生命体がいる可能性も出ている。
惑星ソラリスという映画見たことある?
惑星全体が一つの生命体なんだ。彼には数を発見することはできないだろう。一人しかいないから。人間はひとり、ふたりというので数を認識できる。ソラリスの数学は地球人の数学とは違う。
でも、、、フレンケルさんはソラリスでも数を発見できることを伝えたいという。
イチゴの写真だ。本物も持ってきている。
数を数えることを体験したい。どのイチゴも見た目が少しずつ違う。これを同じものとして1、2と数えるのは違和感がある?
と学生に数えてもらっている。って学生は食べてる(笑)。
でも整数を数を数えないで見つける方法がある。巻きつけ、という方法だ。
歯医者に褒められるように、今から糸ようじを使おうと思う(ちょくちょくジョーク挟んでくるな)。
というのは冗談で、糸を使って見せたいものがある。糸を時計回りに巻き付ける。1、2、3、4、巻きつけることで数を数えることができる。
マイナス1個のイチゴなんて見たことないよね?
反時計回りに巻き付ければマイナスになる。すべての整数が巻き付けで表せる。
知的生命体は糸を自分自身に巻き付ければいいんだ。
しかも級も巻き付けて包むことによって数えられる。
何重にも巻き付けられる。方向も二つある。
だからソラリスのような球状でボールのような生命体でも数を見つけられる。
この2種類の数え方は重要だ。
最初、一人しかいない人間には数は数えられないと思っただろ?でももう一つ方法があったんだ。
これが数学の奥深さだ。
数学の重要性には様々な理由がある。パソコン、スマホの裏側には様々なアルゴリズムがあり、すべて数学に結びついている。
でももう一つ、数学のミステリアスな側面がある。
優れた探偵小説を読むような。人間は答えを知りたがるものだ。
日常の暮らしでは知りえない深遠な世界を知ることができる。
チャールズ・ダーウィンの言葉、
「私は数学の偉大な導きを多少なりとも理解できるだけの勉強をしなかったことをとても後悔している 数学の能力を持つ人はあたかも第六感を持っているように見えるからだ」
を紹介。
ではその第六感で何ができる?
数学とはジグソーパズルのようなものと考えている。
一つ持ってきた。テーブルに広げて、、、あ、ゴッホのさっきの絵だ。
さあ、つなぎ始めよう。
小さなピースをつなぎはじめ、ガリレオの言葉を思い出そう。
でも完成図が入ってなかったら?
数学の研究をすることと似ている。
一人でやるのは楽しくない。友達もやってくれればうれしいだろ?
ピースを一つ一つ組み合わせていくと、小さな島ができる。
友達も別々の島を作り続ける。
これは数学の研究と似ている。数学には様々な分野がある。
数論、調和解析、幾何学。
こうやって組み立てていって、別々の島をつなぎ始めたら、、、さらに組み立てていくことができる。異なる分野のつながりを見つけることは重要。
数学に「分野」というものがあるのは、実は人間の認識不足による幻想ではないか?
(おお、大きく出ましたね)
数学は本当は一つのものかもしれない。
さて、ここでラングランズプログラムについての話をしよう。カナダの数学者、ロバート・ラングランズ(1936-)。
プリンストン高等研究所での写真が示される。今は名誉教授。あのアインシュタインが使っていた部屋を使っていた。アインシュタインは知っていても、ラングランズを知っている人はほとんどいない、なぜだろう、とよく冗談でいう。
ラングランズ・プログラムとは、数論や調和解析など、数学の異なる分野を統一しようとする試みだ。
数学は知識の寄せ集めではない。こんなことは学校では教わらない。
(おっとなんとなく吉田栄作さんのように見えてきたぞ。やっぱりイケメン)
まずは数論。数とはどういうもの?を調べる分野。
次は調和解析。音の分解の研究と思ってもいい。
クラシックの音楽をコンサートホールで聴くことを思おう。一つ一つの音、音符からなっている。それは数学的には音波としてとらえられる。三角関数で表される。
一つ一つは単なる音だが、重なり合って一つになると美しい楽曲になる。
複雑な関数などを細かな要素の重ね合わせで表そうとする分野だ。
次は幾何学。
学校で習うものを思い浮かべると思う。それはユークリッド幾何学。幾何学の一つの分野で、原論という本にまとめられている。平面についての研究。点や線、三角形など。
でもこれは2300年前の研究だ。
非ユークリッド幾何学というのもある。
形についての学問だ。バスケットボールを取り出して表面の三角形を示す。
またアインシュタインによって空間が曲がっていることを知った。
幾何学は様々な形を対象にしている。
ドーナツの表面なんかも。また食べ物で例えてしまったと(笑)。
ここで質問が。
THINKと書いてあるTシャツを着ている割と年配の男性。
分野をつなぐことができる、とわかっているんでしょうか?
と。
とてもいい質問だ、と先生。私がつなぎたいから、あるいはゲームのようにただ面白いからつなごうとしているのか?
そうではない。具体的な問題を解くのが問題。
ラングランズもある問題からこの考えに至った。
数論の問題を考えていたが、数論の分野で解けない、、、そこでこれを調和解析を結び付けた。
言語の翻訳のようなものかもしれない。
ラングランズ・プログラムはある分野で手に負えない難問を別の分野の言語に翻訳する。
突然、美しい答えを得ることもある。
例えば、フェルマーの最終定理、3以上の自然数nに対してx^n+y^n=z^nを満たす自然数x,y,zは存在しないというものがある。350年以上にわたって解けなかった。
これは異なる分野をつなげるという発想で解けた。
つながりが存在するということはわかっている。なぜそのつながりがあるのかがわからない。
ラングランズプログラムはそのつながりについての予想の集合体だ。この50年で相当の進歩があったが、どのようにつながるのか、まだ最終的な答えは明らかになっていない。
どうやってつなげるのか?
秘密の鍵を教えよう。
分野が共通して持っているもの。
それは対称性、Symmetryだ。
数学によって対称性は重要な概念。
数の数え方を思い出してみよう。数を見つける一番簡単な方法は数えることだ。
あ、イチゴみんな食べられちゃってる(笑)
もうひとつ方法はあった。糸を巻き付ける方法だ。
隠された方法ともいえる。
ある視点から見たら当たり前でも、別の視点では隠されていることもある。
分野ごとに対称性はわかりやすかったり隠されていることがある。
対称性が最も重要な概念だ。
誰かに、対称性と聞いて何を思い浮かべる?と聞くとみんな様々な例を挙げてくれる。
雪の結晶なんかが多い。次は蝶。人間の体を例に出す人もいる。
ここでレオナルド・ダ・ヴィンチのあの有名な人体の絵(ウィトルウィウス的人体図)を例に挙げる。なぜ対象だと感じる?
ペットボトルの水を2つ持ち出す。底が丸くてふたが白いもの、底が四角でふたが青いもの。ここでききたい。手を挙げて。
どちらが対称性が高い?まるいほうと思う人?たくさん。四角いほう?これは少ない。
ちゃんとした証明が必要だ。
対称性とは物体の形や位置を変えない動かし方、変換のこと。
またはある変換に対して不変である性質。
丸いボトルで形や位置が変わらないようにするには?軸を基準にしてどのように回転させても変わらない。
四角いボトルでは回したら90、180、270°の時だけ変わらない。
まとめると、
丸いボトルはあらゆる角度で変化しない。無限の対称性。
四角いボトルは4つの対称性しかない。
つまり丸いボトルのほうがより多くの対称性を持つ。
次のステップに進もう。
このことを抽象的な図形で表せないか?
丸いボトルはどんな図形として表せる?
円。と学生が答える。
正解。
円として表せる、それが数学だ。
ボトルの底が丸いから、それをなぞって円になったわけではないことに注意しよう。
この円は現実に実態があるものではない。頭の中にだけ存在する、抽象的なものだ。
同じように四角いボトルを見てみると、4つの点で表せる。四角形じゃない。
この図形をより深く理解できないか?
ボトルを30°回転させてみる。形は変わらない。さらに20°。最終的に50°の回転をしたことになる。つまり、回転は足し合わせることができる。円上のどの2点をとっても3点目が作れるということになる。これを合成と呼ぶ。
そこから群として捉えられる。
円の場合の合成は0°~360°の値になるが、これが隠されていた性質だ。もう一つのペットボトルを取り出す。底は丸い。
同じ対称性の群を持っている。底が丸いボトルは同じ対称性の群を共通に持っている。丸いテーブルでも、丸いグラスでも。
対称性の群が円になるものが丸い、ということになる。
対称性の群は他にもある。
入れ替えという変換をする。また食べ物の登場だ。
今度はオレンジだ。健康的な生活の秘訣は野菜や果物を食べること、今日は学生も多いからそのことを伝えたかったとまたジョーク。
いくつかあれば入れ替えの操作ができる。
あるものと他のものを入れ替える。黒板に書いたほうがわかりやすい。
三つの物体がある。
① ② ③
例えば①が②に、②は①に、③はそのまま。
これが一つの入れ替え方。オレンジでもやってみる。
3つの場合は何通りある?
一つ目には3つの選択肢がある。二つ目には2つの、三つ目には選択肢ないので、6個だ。
N個の場合は?
n(n-1)(n-2)・・・1=n!、階乗だ。
物体の数よりも入れ替えの数のほうが多い。
立て続けに回転させることでボトルは合成できた。
では入れ替えは?
入れ替えも立て続けに行っても新しい入れ替え方ができる。
ここまで何を学んだかをまとめて今日の終わりにしたい。
数論・調和解析・幾何学が対称性という同じ性質を持っている。
今日は幾何学について回転などをさせてどのように対称性が現れるか見てみた。
数を数えるのに2種類あったように、対称性の現れ方は他にもある。
次回は数論の対称性についてみてみる。ガロアが登場する。
次は調和解析、そして次は物理。
対称性の理解がラングランズプログラムにつながっている。
※番組に協力されているのは
小山伸也さんだそうです。
**
*
ミレニアム問題とは,解決したら100万ドルもらえる重大な7つの問題です。7つのうちポアンカレ予想だけは既に解かれています。
残り6つのうち,主張が比較的理解しやすいのはP≠NP予想とリーマン予想です。そこでこのページではP≠NP予想の主張について解説します。
残り6つのうち,主張が比較的理解しやすいのはP≠NP予想とリーマン予想です。そこでこのページではP≠NP予想の主張について解説します。
大雑把な解説
P≠NP予想は計算量理論の話になります。
問題の集合(クラス)PとNPが等しくないという予想です。
問題の集合(クラス)PとNPが等しくないという予想です。
- 「P」というのは多項式時間で解ける問題のクラス,つまり,「パソコンで解きやすい」問題です。
- 「NP」というのは多項式時間で正解が本当に正しいか判定できる問題のクラスです。
もし,P=NPなら今まで解けなかったNPの問題が全て多項式時間で解けるようになってしまうのでそんな都合の良いことはないだろうという予想です。ちなみに,P=NPだと素因数分解の難しさを利用した現代の主要な暗号は破られてしまいます。
クラスPとは
Pというのは入力サイズに対して多項式時間で解ける問題のクラスです。
多項式時間かどうかというのは,四則演算や比較などのコンピュータ上での基本的な演算の回数で見積もります。
多項式時間かどうかというのは,四則演算や比較などのコンピュータ上での基本的な演算の回数で見積もります。
コンピュータを用いて指数時間かかってしまうような問題は現実的な時間で解くことができないのです。
(n2 回計算が必要な問題はn=10000 くらいでも余裕で計算できるが,2n 回計算が必要な問題はn=100 でも到底計算できない)
(
例1
与えられたグラフが一筆書きできるか判定する問題はPである。なぜなら,各頂点の次数が偶数かどうかを調べればよいので,高々「頂点の数×辺の数」くらいの演算をすればよい。→オイラーグラフの定理とその証明
クラスNPとは
NPというのは多項式時間で正解が本当に正しいか判定できる問題のクラスです。
答えを見つけるのは難しいかもしれないが,答えの正しさを証明するのなら簡単だ,という問題です。
答えを見つけるのは難しいかもしれないが,答えの正しさを証明するのなら簡単だ,という問題です。
例2
ハミルトン閉路問題(頂点を1回ずつ通って元に戻ってくる道があるのか判定する問題)はNPである。実際にそのような道を探すのは難しい(多項式時間で解く方法は発見されていない)が,答えが与えられたらそれが確かに正しいということは簡単に確認できる。
オイラー閉路問題(例1)とハミルトン閉路問題(例2)は一見似ていますが,例1は簡単で例2は難しいというのは不思議ですね。
ちなみに,ハミルトン閉路問題は有名な巡回セールスマン問題の特殊ケースとみなすことができます。
PとNPの包含関係

多項式時間で解けるなら,多項式時間で確認できるので,Pに属する問題はNPにも属します。つまりNPはPを含んでいます。
よって,P≠NP予想は,「NPに属するのにPに属さない問題(図の赤い部分)」があるのかどうかをめぐる問題ということになります。
そして,ハミルトン閉路問題など実際に図の赤い部分に属すると思われる問題が何千も見つかっているのです。しかし,それらがPに属さないことは証明されていません。
よって,P≠NP予想は,「NPに属するのにPに属さない問題(図の赤い部分)」があるのかどうかをめぐる問題ということになります。
そして,ハミルトン閉路問題など実際に図の赤い部分に属すると思われる問題が何千も見つかっているのです。しかし,それらがPに属さないことは証明されていません。
P≠NP予想が解けたら約一億円もらえるのでみなさん挑戦してみてください



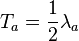


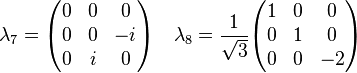
![[T_a,T_b]=i\sum_{c=1}^8 f_{abc}T_c](https://upload.wikimedia.org/math/6/0/e/60e7e83ecbff9c42c430882c423028df.png)


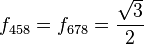
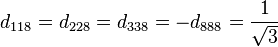
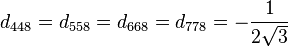
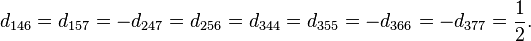








12 Comments:
(udd) Y (uud)
中性子 n0____|____P+ 陽子
/\ |1 /\
/ \ | / \
/ \ | / \
/ \|/ \
--〈--------X--------〉-
Σ ー \ー1/2 Σ 0|λ0 ー1/2 /Σ+
ー1 \ / | \ / 1
\ / | \ /
\/___|___\/
三ー |ー1 三0
3Dを平面に直すと上のような図になる。
時間は左から右か?
一方、ミンコフスキー時空図が非対称性を示す。
NAMs出版プロジェクト: ハドロンの分類図、SU(3)の図
http://nam-students.blogspot.jp/2015/12/su.html
感想: NHK数学ミステリー白熱教室 - とね日記
http://blog.goo.ne.jp/ktonegaw/e/b0d53d030bf82e8016a1071fadb16063
第4回の放送でようやくラングランズ・プログラムの鍵となる「ラングランズ双対群」が紹介され、物理学を含めて4つの世界のつながり方の説明が完結した。対称性は直観的に理解しやすい概念だが、双対性の概念についてもボルシチのレシピの例をあげるなど、一般視聴者にもイメージできるように説明されていたのがよかったと思う。
最終回まで見てみると、今回の番組は僕の期待をはるかに超えた中身のあるものだったと思う。今後の数学や物理学の発展も楽しみだが、このような科学教養番組もこれからどのようなものが作られていくのかについても楽しみだ。
今回の番組で取り上げられたのは「対称性」と「双対性」であり、ともに群論であらわされる性質だ。著書では番組で取り上げられていたことをより深く知ることができ、数学の統一という大目標が夢物語ではないことを実感できるだろう。放送を見逃した方にもこの本はありがたい。
「数学の大統一に挑む:エドワード・フレンケル」(Kindle版)(紹介記事)
0061 名無しのひみつ@転載は禁止 2016/03/19 05:23:20
因みに学び直すなら最初は物理に絡めた数学がお勧め
例えば、テンソル解析は相対論と結びつけて
関数空間論や連続群論は量子論と結びつけて理解すると分かり易いかも
返信 ID:1YwHORcl(25)
0062 名無しのひみつ@転載は禁止@転載は禁止 2016/03/19 05:25:28
そこだね
テンソル解析を相対論とか弾性体理論なしに作った数学者のすごさなんだな
尋常じゃないよ
0066 名無しのひみつ@転載は禁止 2016/03/19 05:35:27
>>62
いや、それはちょっと違うと思う
例えば、テンソル解析の‟主流”は解析力学に動機づけされて現れて
一般相対論の定式化ととも発展しているよ
まあ天才リーマンは偉大な例外だけどね
1 ID:1YwHORcl(25)
0067 名無しのひみつ@転載は禁止 2016/03/19 05:38:30
物理学者自身がオーダーメイドで新しい数学を創始するという事もあるしな。
それで、ペレルマンのように後から数学が物理学に近づくという事もある。
1 ID:sBA9vSHD(36)
0068 名無しのひみつ@転載は禁止 2016/03/19 05:38:45
>>66追加
いわゆるリーマン幾何学は数学では浸透せずに一般相対論のcontextで「再発見」されましたから
ID:1YwHORcl(25)
0069 名無しのひみつ@転載は禁止 2016/03/19 05:39:36
>>1
>> 国際数学界はその翌日、彼の証明を公式に認めた。
講演発表のは間違いがあったんだろ?
ID:OF4OqpuC(1)
0070 名無しのひみつ@転載は禁止 2016/03/19 05:41:59
>>67
その顕著な例の1つが超関数論だね
ディラックのデルタ関数から始まった
今では子供でも知っているこの超関数が数学界では受け入れられなかったわけだから
http://itest.2ch.net//test/read.cgi/scienceplus/1458321239/-100
>>29
任意の数を6で割った余り0〜5のうち、0,2,4になるものは2の倍数、3も全体として3の倍数、よって1か5(-1)のみになる
で、こういう剰余の方法は超高等なものだが>>1も含めて数論、現代数学一般で駆使される
返信 4 ID:uKp/47tP(1)
0049 名無しのひみつ@転載は禁止 2016/03/19 05:03:48
>>42
同じ賞でもレベルの違いはあるだろうな。
正確には数学が物理学よりも上位にあると思うと言うべきだったのかな。
ID:sBA9vSHD(36)
0050 名無しのひみつ@転載は禁止 2016/03/19 05:04:11
数学のノーベル賞ってフィールズ賞じゃないの?
ID:O/ul2tvB(1)
0051 名無しのひみつ@転載は禁止 2016/03/19 05:06:14
>>48
美しい・・・・・
1 ID:hMVgNyEJ(4)
0052 名無しのひみつ@転載は禁止 2016/03/19 05:08:14
>>48
言い忘れたがこれは2と3を除いての話な。
例えば5と7は6の前後、11と13は12の前後だ。
それ以降のどの素数も6n+1か6n-1で表される。
1 ID:sBA9vSHD(36)
数学の大統一に挑む (文春e-book)
Kindle版
販売: 株式会社 文藝春秋
谷山の自殺、三島の映画、人種差別
不合理なものが数学の美しさを際立たせる
【インタビュー】 宇宙の謎に迫る 世界最先端の “すごい実験” ~究極の物の“中身”、素粒子を知る~ 素粒子物理学者・多田将 さん [無断転載禁止]©2ch.net
29コメント13KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1朝一から閉店までφ ★@無断転載は禁止2017/08/05(土) 08:41:25.96ID:CAP_USER>>18>>20
宇宙の謎に迫る
世界最先端の
“すごい実験”
~究極の物の“中身”、素粒子を知る~
素粒子物理学者・多田将 さん
茨城県東海村。太平洋を臨むこの小さな村に、高エネルギー加速器研究機構と日本原子力開発研究機構が共同運営する、世界最先端の大強度陽子加速施設、J-PARCはある。なかでも、日本に3度ノーベル賞をもたらした素粒子物理学の分野で、誰にもマネのできない“すごい実験”を行っているのが、ニュートリノ実験施設だ。
多田将さんは、この施設を設計した素粒子物理学者で、宇宙の謎に迫る壮大な実験を積み重ねている。
金髪に迷彩服姿という外見もさることながら、わかりやすい語り口で年間30回もの講演をこなしたり、実験施設をイチから設計するなど、その仕事ぶりも型破りだ。「好き嫌いでは生きてこなかったからでしょうね」――プロフェッショナルに徹する多田さんの人生哲学に迫った。
取材・文:高松夕佳/写真:仲田絵美/編集:川村庸子
世紀の大発見を目指して
「素粒子物理学」というと、とてつもなく難しく感じてしまうのですが、そもそも「素粒子」って何ですか?
多田 素粒子とは、自然界に存在するものを分解していったときにこれ以上分割できない最も小さな粒子のことです。
自然界で最も大きなものは、宇宙です。人間が観測できる宇宙の大きさは、1,000,000,000,000,000,000,000,000,000(一千抒「じょ」)メートル。途方もない大きさですよね。これを扱うのは宇宙物理学です。我々の住む地球の直径は10,000,000メートル。この太陽系の星々を扱うのが惑星物理学です。
人間の大きさは約1メートル、その中の内臓は約0.1メートルで、これが医学の領域です。内臓を構成する細胞(0.00001メートル)は生物学、その細胞を形作る分子の大きさまでを扱うのが化学です。分子を分解してできるのが原子で、その中身の原子核は原子核物理学が扱います。
素粒子物理学はさらにその先、0.000000000000000001メートルよりも小さい素粒子を相手にする学問です。
===== 後略 =====
全文は下記URLで
http://toshin-sekai.com/interview/20/
物理学において素粒子(そりゅうし、英: elementary particle)とは、物質を構成する最小の単位のことである。基本粒子とほぼ同義語である。
目次
概要 編集
標準模型による素粒子の相互作用の説明
素粒子はそれが従う統計によって二種類に分類され、フェルミ統計に従う粒子をフェルミ粒子、ボース統計に従う粒子をボース粒子と呼ぶ。現時点で存在が知られているフェルミ粒子はクォークとレプトンとに分類される。一方、現時点で知られているボース素粒子には、素粒子間の相互作用を伝達するゲージ粒子と、素粒子に質量を与えるヒッグス機構に関連して現れるヒッグス粒子とがある。ゲージ粒子のうち、重力を媒介するとされる重力子は未発見である。
素粒子の大きさは分かっておらず、大きさが無い(点粒子)とする理論と、非常に小さいがある大きさを持つとする理論がある。
標準模型(標準理論)では素粒子には大きさが無い(点粒子)ものとして扱っており、現時点では実験結果と矛盾が生じていない。ただし、点粒子は空間が最小単位の存在しない無限に分割可能な連続体であることを前提としているが、標準模型で扱うスケールより15桁以上小さいスケール(プランク長スケール)においては、空間が連続的であるか離散的であるかは判明していない。離散的である場合には点粒子として扱えない。
超弦理論においては全ての素粒子は有限の大きさを持つひもの振動状態であるとされる。
我々が普段目にする物質は(微小な、あるいは大きさが無い)素粒子からできているにも関わらず、有限の大きさを持っている。それは、複数の素粒子が運動する有限の領域が、ハドロンや原子などの大きさを持つ粒子を構成することによる。
素粒子のうちほとんどのものは、自然界に単独で安定的に存在しているわけではないので、宇宙線の観測や加速器による生成反応により発見・研究された。素粒子の様々な性質を実験で調べ、それを理論的に体系化していくこと、及び理論的に予言される素粒子を実験で探索していくことが、素粒子物理学の研究目的である。
クォーク(quark)とは、素粒子のグループの一つである。レプトンとともに物質の基本的な構成要素であり、クォークはハドロンを構成する。クオークと表記することもある[1]。
クォーク
Quark structure proton.svg
ハドロンである陽子は、2つのアップ (u) と1つのダウン (d) による3つのクォークからなる。
型数 6 (アップ、ダウン、チャーム、ストレンジ、トップ、ボトム)
組成 素粒子
粒子統計 フェルミ粒子
グループ クォーク
世代 第一、第二、第三世代
相互作用 強い相互作用
弱い相互作用
電磁相互作用
重力相互作用
反粒子 反クォーク (q)
記号 q
崩壊粒子 安定
電荷 +2⁄3 e, −1⁄3 e
色荷 持つ
スピン 1⁄2
バリオン数 1⁄3
クォークという名称は、1963年にモデルの提唱者の一人であるマレー・ゲルマンにより、ジェイムズ・ジョイスの小説『フィネガンズ・ウェイク』中の一節 "Three quarks for Muster Mark" から命名された[2][3] 。
(udd) Y (uud)
中性子 n0____|____P+ 陽子
/\ |1 /\
/ \ | / \
/ \ | / \
/ \|/ \
--〈--------X--------〉-
Σ ー \ー1/2 Σ 0|λ0 ー1/2 /Σ+
ー1 \ / | \ / 1
\ / | \ /
\/___|___\/
三ー |ー1 三0
クォーク=素粒子の一種
クォークモデルは、1950年代から1960年代に渡って発見された非常に多くのハドロンを系統立てて分類するために
開発され、1960年代後半から現在までの実験によってその正しさが検証されている。これらの実験的証拠により、
ハドロンは"基本粒子"ではなく、それを構成する"価クォーク"が基本粒子であると考えられている。クォークモデル
は価クォーク単位でハドロンを分類する。価クォークとは、ハドロンの量子数の実体を担っているクォークおよび
反クォークである。
これらの量子数はハドロンの種類を同定するためのラベルであり、二種類に分けることができる。一つは、ポアンカレ
対称性を持つJPCである。ここで、J、PおよびCはそれぞれ全角運動量、パリティ対称性およびチャージ対称性である。
二つ目は、アイソスピン、ストレンジネスおよびチャームなどのフレーバー量子数である。クォークモデルは八道説の
分類法に従っている。(#中間子および#バリオン参照)
全てのクォークにはバリオン数1⁄3が割り当てられている。アップ、チャームおよびトップクォークは電荷+2⁄3を持ち、ダウン、
ストレンジおよびボトムクォークは電荷-1⁄3を持つ。また、反クォークはクォークと反対の符号の量子数を持つ。クォークは
スピン-1⁄2粒子、つまりフェルミ粒子である。
中間子は価クォーク-反クォークの対で構成されており、バリオン数は0となる。一方、バリオンは三つのクォークで構成されており、
バリオン数は1となる。この記事の具体例では、アップ、ダウンおよびストレンジフレーバーのクォークモデル(これは近似的にSU(3)
対称性を形成する)について議論する。フレーバーの数をさらに増やす一般化も存在する。
【素粒子】「クォーク融合」は核融合に対し約8倍強力との研究結果。研究者「発表すべきでないかもと思った」
120コメント29KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1しじみ ★2017/11/08(水) 22:07:02.57ID:CAP_USER>>4>>58>>59>>89
爆弾はつくれないと判明
テルアビブ大学とシカゴ大学からなる研究チームが、クォークとして知られる素粒子グループどうしを融合させた際に放出されるエネルギー量が、
核融合反応の約8倍にものぼることがわかったと発表しました。
クォークとは、物質を構成する原子、を構成する陽子と中性子など、を構成する素粒子、を構成する粒子のグループのひとつ。
クォークにも6つの種類があるとされます。クォーク自体も6つのフレーバーと呼ばれる種類があり、
それぞれアップ、ダウン、ストレンジ、チャーム、トップ、ボトムに分類することができます。
スイス・ジュネーブ郊外にあるCERNの大型ハドロン衝突型加速器(Large Hadron Collider : LHC)では、
原子を高速で衝突させてこうした素粒子に分離させ、それぞれの粒子に関する研究が行われています。
そしてこれまでの研究では、クォークどうしが結合してバリオンなど複合粒子を構成する際に、
大きなエネルギーが関わっていることが示されていました。
研究者らは、バリオン生成の研究をすすめるうちに、
チャームクォーク2つを融合させてバリオンを構成するためには130MeV(1億3000万電子ボルト)のエネルギーが必要であることを発見しました。
そして、その際には12MeVの余剰エネルギーが放出されることがわかりました。
研究者らはこの放出エネルギーに興味を持ち、より重い、つまりエネルギーを持つと考えられるボトムクォーク2つを使って同様の実験をしてみました。
すると230MeVのエネルギーで発生したボトムクォークの融合時には約138MeVが放出され、
残りはより軽いクォークからなるバリオンに変化することを突き止めました。
これは水素爆弾のエネルギー放出源となる水素核融合に対して8倍以上という莫大なエネルギー量です。
あまりのエネルギーの大きさに、研究者らはこの研究結果は公表すべきではないとさえ感じたとしています。
しかし、その後の研究の結果、このエネルギーの放出時間はわずかに1ピコ秒ほどしかなく、
これでは水素爆弾のような連鎖的な反応を引き起こすには至らないことがわかりました。
研究者らは、現状ではこの研究結果が完全に理論上の話だと認めています。
そしてLHCでこの現象を実験することも可能だとしつつも、現状ではそれを実行しようとは考えていないとのことです。
ちなみに、電子ボルトとは自由空間内で1つの電子が1Vの電圧で加速される際のエネルギーのこと。
LHCでは2013~2015年にかけて実施された強化工事により、13TeV(13兆電子ボルト)ものエネルギーを扱えるようになっています。
関連ソース画像
http://o.aolcdn.com/hss/storage/midas/ca2bf8325aa5e8ea80c07ce795e8bfaf/205842199/nature.jpg
engadgetjp
http://japanese.engadget.com/2017/11/08/8/
(udd) Y (uud)
中性子 n0____|____P+ 陽子
/\ |1 /\
/ \ | / \
/ \ | / \
/ \|/ \
--〈--------米--------〉-
Σ ー \ー1/2 Σ 0|λ0 ー1/2 /Σ+
ー1 \ / | \ / 1
\ / | \ /
\/___|___\/
三ー |ー1 三0
クォーク=素粒子の一種
クォークモデルは、1950年代から1960年代に渡って発見された非常に多くのハドロンを系統立てて分類するために
開発され、1960年代後半から現在までの実験によってその正しさが検証されている。これらの実験的証拠により、
ハドロンは"基本粒子"ではなく、それを構成する"価クォーク"が基本粒子であると考えられている。クォークモデル
は価クォーク単位でハドロンを分類する。価クォークとは、ハドロンの量子数の実体を担っているクォークおよび
反クォークである。
これらの量子数はハドロンの種類を同定するためのラベルであり、二種類に分けることができる。一つは、ポアンカレ
対称性を持つJPCである。ここで、J、PおよびCはそれぞれ全角運動量、パリティ対称性およびチャージ対称性である。
二つ目は、アイソスピン、ストレンジネスおよびチャームなどのフレーバー量子数である。クォークモデルは八道説の
分類法に従っている。(#中間子および#バリオン参照)
全てのクォークにはバリオン数1⁄3が割り当てられている。アップ、チャームおよびトップクォークは電荷+2⁄3を持ち、ダウン、
ストレンジおよびボトムクォークは電荷-1⁄3を持つ。また、反クォークはクォークと反対の符号の量子数を持つ。クォークは
スピン-1⁄2粒子、つまりフェルミ粒子である。
中間子は価クォーク-反クォークの対で構成されており、バリオン数は0となる。一方、バリオンは三つのクォークで構成されており、
バリオン数は1となる。この記事の具体例では、アップ、ダウンおよびストレンジフレーバーのクォークモデル(これは近似的にSU(3)
対称性を形成する)について議論する。フレーバーの数をさらに増やす一般化も存在する。
物理と数学の奇妙な一致
y|
|p
____|____
/\ | /\
q/U+\ | /V+\q
/ \ | / \
__/Tー____\|/____T+\_→
\ /|\ / t
\ / | \ /
p \Vー/ | \Uー/ p
\/___|___\/
|q
SU(3)の図
https://ja.wikipedia.org/wiki/特殊ユニタリ群
n次の特殊ユニタリ群(とくしゅユニタリぐん、英語: special unitary group)SU(n) とは、行列式が1のn次ユニタリ行列の為す群の事である。群の演算は行列の積で与えられる。
特殊ユニタリ群 SU(n) はユニタリ群 U(n) の部分群であり、さらに一般線型群 GL(n,C)の部分群である。
特殊ユニタリ群は素粒子物理学において、電弱相互作用のワインバーグ=サラム理論や強い相互作用の量子色力学、あるいはそれらを統合した標準模型や大統一理論などに出てくる。
【物理学】反物質の「陽電子」、雷から生成…証拠を発見
60コメント18KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1しじみ ★2017/11/23(木) 16:48:31.90ID:CAP_USER
論文が23日、英科学誌ネイチャーに掲載される。
チームは2006年から、雷が多発する日本海沿岸などで、
落雷時に放出されるガンマ線(放射線)について調べる地上観測を実施。
今年2月、新潟県柏崎市の沖合数百メートルで発生した落雷の後、反物質ができたことを示す微弱なガンマ線を検出した。
データの分析から、この現象は
〈1〉雷から放出された強力なガンマ線が大気中の窒素の原子核に当たり、中性子が1個飛び出る
〈2〉中性子を失った窒素が別の物質に変化する間、通常の電子と逆にプラスの電気を帯びた反物質の「陽電子」を放出する
〈3〉陽電子が大気中の電子と衝突し、微弱なガンマ線が出た――と考えられるという。
窒素が別の物質に変化するまでの約10分間、雲の中には数兆個の陽電子が存在したとみられる。
続きはソースで
読売新聞
http://www.yomiuri.co.jp/science/20171122-OYT1T50107.html
【物理】「マヨラナ粒子」 80年以上前に予言された幻の粒子の存在を世界で初めて実証…京大グループ
60コメント21KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1野良ハムスター ★2018/07/12(木) 09:06:54.38ID:CAP_USER>>34
80年以上前に存在が予言された幻の「マヨラナ粒子」が実際に存在することを世界で初めて実証したと、京都大などのグループが12日付の英科学誌ネイチャーに発表した。電気を通さない固体の中で、電子があたかもマヨラナ粒子のようにふるまう現象を観測したという。将来的には量子コンピューターなどへの応用が期待される。
マヨラナ粒子は、粒子とも反粒子とも区別のつかない「幻の粒子」と言われ、1937年にイタリアの物理学者、エットーレ・マヨラナが理論的に存在を予言した。電気を帯びず極めて質量の小さな素粒子「ニュートリノ」がその本命と考えられているが、証明には至っていない。一方、特殊な条件下の超電導体などでは、電子がマヨラナ粒子のようにふるまう可能性が指摘され、その決定的証拠をつかもうと各国で研究が本格化している。
笠原裕一・京大准教授(物性物理学)らは、東京工業大のチームが合成した磁性絶縁体「塩化ルテニウム」を用い、その内部を伝わる熱の流れが磁場によってどの程度曲がりやすくなるかを、磁場を変化させながら測定した。
その結果、ある範囲の磁場では、磁場や温度を変えても、曲がりやすさの値が普遍的な値の2分の1で一定になった。熱を運ぶ粒子が電子の半分の自由度を持っていることを意味し、そのような性質があるマヨラナ粒子が現れたと考えないと説明が付かないという。
マヨラナ粒子は外部からの影響に対して強く、粒子が持つ情報を安定的に保てるため、量子コンピューターの素子としての応用に期待がかかる。笠原准教授は「これが普遍的な現象なのか、他の物質でも確かめたい。量子コンピューターの実現につながるか今は全く分からないが、その基盤を発見したと言えるのではないか」と話す。【菅沼舞、阿部周一】
■ノーベル賞級の成果
木村昭夫・広島大教授(物性物理学)の話 世界で発見レースが繰り広げられる中、大半の研究がターゲットにしていた超電導体とは別の物質、別の方法を用いてマヨラナ粒子の存在を直接的に示したインパクトは大きい。液体ヘリウムで冷却可能な温度(5ケルビン)で観測できたことも、今後の実験や応用に期待を広げる。ノーベル賞に値する重要な成果だ。
【ことば】粒子と反粒子
電子に対する陽電子、陽子に対する反陽子のように、物質を構成する粒子には質量は同じだが電荷が正負逆の反粒子がある。両者は出合うと消滅する。宇宙誕生時は粒子と反粒子が同数できたはずだが、今の宇宙は粒子ばかり。もし宇宙で最も数が多いニュートリノが粒子と反粒子の区別がつかないマヨラナ粒子だとすると、粒子と反粒子の数が非対称になった謎に説明が付くと期待されている。
毎日新聞2018年7月12日 02時30分(最終更新 7月12日 02時38分)
https://cdn.mainichi.jp/vol1/2018/07/12/20180712ddm001010024000p/9.jpg
https://mainichi.jp/articles/20180712/k00/00m/040/178000c
コメントを投稿
<< Home