1 :
2016/06/14(火) 12:23:18.75 ID:CAP_USER
共同発表:ガラスの「形」を数学的に解明~トポロジーで読み解く無秩序の中の秩序~
http://www.jst.go.jp/pr/announce/20160614/index.html
ポイント
東北大学 原子分子材料科学高等研究機構(WPI-AIMR)の平岡 裕章 准教授、中村
壮伸 助教を中心とした研究グループは、統計数理研究所(ISM)および科学技術振興機構(JST)と共同で数学的手法を開発することで、ガラスに含まれ
る階層的な幾何構造を解明することに成功しました。
周期性を持たないガラスの原子配置構造は非常に複雑であり、その構造を理解するために、適切な記述法を開発することが長年求められていました。本研究グ
ループは、トポロジー注1)を応用することでこの問題を解決することに成功しました。さらに、ここで開発された数学手法は物質に特化しない普遍的なもので
あることから、情報ストレージや太陽光パネルなどのガラス開発に加え、マテリアルズインフォマティックス注2)なども含めた幅広い材料開発への応用が期待
されます。
本成果は、平成28年6月13日の週(米国東部時間)に、米国科学アカデミー紀要(PNAS)「Proceedings of the National Academy of Sciences」オンライン速報版に掲載されます。
(以下略)
2 :
名無しのひみつ@無断転載は禁止
2016/06/14(火) 12:40:45.21 ID:20q5TdAn
無秩序にも「秩序」がある。それを数学的に記述するんだね。
3 :
名無しのひみつ@無断転載は禁止
2016/06/14(火) 12:41:22.81 ID:dxSRlr6i
全然分からんがや
4 :
名無しのひみつ@無断転載は禁止
2016/06/14(火) 12:48:43.97 ID:iKII4TRq
材料系は東北大学強いなぁ
5 :
名無しのひみつ@無断転載は禁止
2016/06/14(火) 12:52:15.54 ID:4nJtOAw1
http://www.jst.go.jp/pr/announce/20160614/icons/zu1.jpg
意外に面白いな。
> 純粋に「データの形」を扱う今回の手法は、ガラスに限らないその他の材料やより一般のデータ解析への応用も可能とします。
> 膨大な原子配置データや実験画像データに対するマテリアルズインフォマティックスへの展開や、ビッグデータ解析へブレークスルーをもたらす手法に発展することが予想されます。
発展性もある。
_______________
平成28年6月14日
東北大学 原子分子材料科学高等研究機構(WPI-AIMR)
情報・システム研究機構 統計数理研究所(ISM)
科学技術振興機構(JST)
ガラスの「形」を数学的に解明
~トポロジーで読み解く無秩序の中の秩序~
東北大学 原子分子材料科学高等研究機構(WPI-AIMR)の平岡 裕章 准教授、中村
壮伸 助教を中心とした研究グループは、統計数理研究所(ISM)および科学技術振興機構(JST)と共同で数学的手法を開発することで、ガラスに含まれ
る階層的な幾何構造を解明することに成功しました。
周期性を持たないガラスの原子配置構造は非常に複雑であり、その構造を理解するために、適切な記述法を開発することが長年求められていました。本研究グループは、
トポロジー注1)を応用することでこの問題を解決することに成功しました。さらに、ここで開発された数学手法は物質に特化しない普遍的なものであることから、情報ストレージや太陽光パネルなどのガラス開発に加え、
マテリアルズインフォマティックス注2)なども含めた幅広い材料開発への応用が期待されます。
本成果は、平成28年6月13日の週(米国東部時間)に、米国科学アカデミー紀要(PNAS)「Proceedings of the National Academy of Sciences」オンライン速報版に掲載されます。
<研究の背景>
ガラスは結晶とは異なり原子配列に周期性を持たないことから、構造を適切に表現する記述法としていまだ満足なものが得られていません。従来の手法では、各
原子の近傍に関する短距離構造について調べることは可能ですが、ガラスのように乱れた3次元原子配置をもつ系に対しては有効ではありません。特に近年の研
究では、ガラスの構造を理解するには、より広範囲の原子で構成される中距離構造を理解する必要性が報告されており、現在多くの研究者が実験的・理論的にガ
ラス構造の解明に取り組んでいます。このような新たな記述法の開発は、基礎科学としては「ガラスとは何か」という長年の大問題への理解を深めるものであ
り、また産業的には情報ストレージや太陽光パネルなどのガラス材料開発に直結する重要な意味を持ちます。中距離構造を記述する難しさは、(1)多くの原子
からなる多体系の特徴をどのように記述するか、および(2)短距離から中距離までのマルチスケール性をどのように扱うかにあり、このような困難を克服しか
つ材料に依存しない普遍的な新手法の開発が強く望まれていました。
<研究の内容>
このたび、東北大学 原子分子材料科学高等研究機構を中心とした研究グループは、ガラスの原子配置に含まれる中距離秩序構造を記述できる数学的手法を開発し、それを用いてガラスの階層的な幾何構造を抽出することに成功しました。開発された数学的手法は
パーシステントホモロジー注3)と呼ばれるトポロジーにおける概念を用いており、原子配置を空間内の点の集まりとみなし、そこに含まれるリングや空洞といった「穴」に着目するマルチスケールデータ解析を可能とします。これにより酸化物ガラスや金属ガラスの代表的な例(SiO
2やCuZr)に対して、
分子動力学法注4)を用いて各物質の原子配置を構成しパーシステントホモロジーを適用することで、液体とガラス状態の内部構造の違いを幾何学的に特徴付けることに成功しました(
図1、
図2)。特に、ガラス状態では原子配置のリング構造に階層性を持った秩序構造が存在することを見出しました。ここで得られた新たな知見をもとに、
第一シャープ回折ピーク(FSDP)注5)の実空間幾何構造としての特徴づけや、ガラスの硬さの起源にあたる中距離秩序構造の記述にも成功しました。
<今後の展望>
今回の数学的手法を用いたガラスの構造解析に関する成果は、ガラスの基礎研究から応用研究までの広い分野に大きなインパクトを与えるものです。今後基礎研
究としては、パーシステントホモロジーを用いたガラス転移の特徴づけや、剛性や粘性をはじめとした物性と原子配置の相関について理解が進むことが予想され
ます。また応用の立場からは、ガラス材料を用いた高機能な記録材料・記録媒体や太陽光パネルなどの開発へ適用されることが期待されます。さらに数学的手法
の最大の特徴はその普遍性であり、純粋に「データの形」を扱う今回の手法は、ガラスに限らないその他の材料やより一般のデータ解析への応用も可能としま
す。膨大な原子配置データや実験画像データに対するマテリアルズインフォマティックスへの展開や、ビッグデータ解析へブレークスルーをもたらす手法に発展
することが予想されます。
なお、本成果は、文部科学省 世界トップレベル研究拠点プログラム(WPI)、JST
CREST「ソフトマター記述言語の創造に向けた位相的データ解析理論の構築」(研究代表者:平岡 裕章)、JST
さきがけ「トポロジカルデータ解析に基づくアモルファス構造の包括的記述と特徴抽出」(研究者:中村 壮伸)、JST
SIP「マテリアルズインテグレーションへの数学的アプローチ技術開発」(研究責任者:西浦 廉政)などの援助によって得られました。
<参考図>
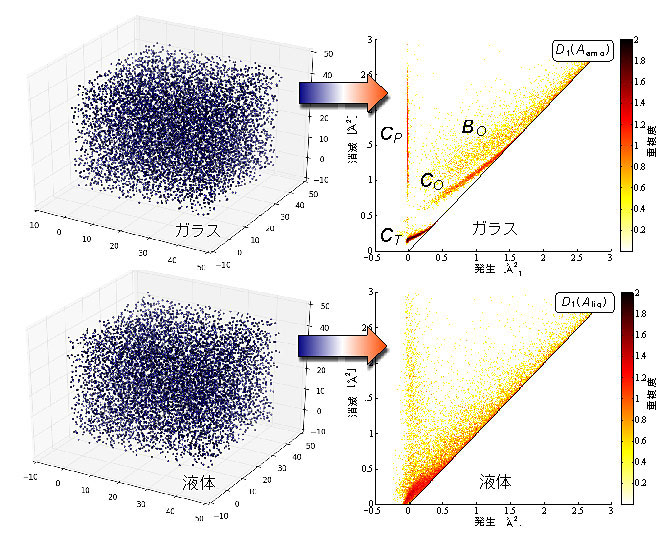
図1 SiO2の原子配置(左)とそのパーシステントホモロジー(右)
ガラスは液体と異なり3つの曲線CP、CT、COとBOのような帯状領域を持つ。数学解析を行うことでこれらの曲線がガラスの形を特徴づけていることがわかる。
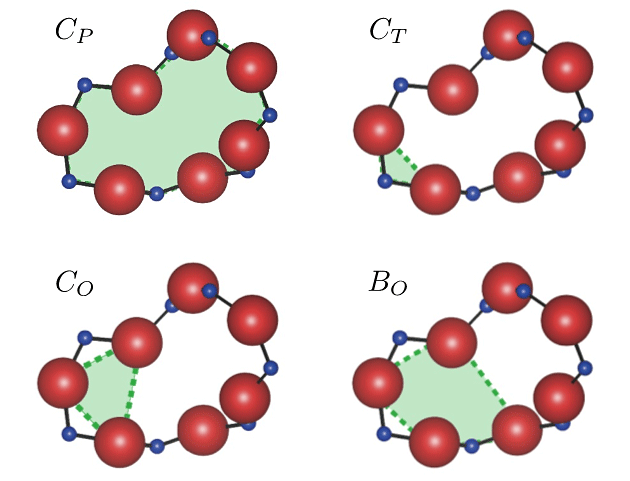
図2 SiO2ガラスのパーシステントホモロジー(図1右上)に対応する典型的なリング構造
パーシステントホモロジーは緑色のリングを捉えている。ここで赤球はO原子、青球はSi原子を表す。
<用語解説>
- 注1) トポロジー
- 物の形を連続変形した際に保たれる性質に着目した数学の1分野です。例えば輪ゴムとコーヒーカップは、互いにリング形状を保ちながら移り合うので
同じものと見なされます。位相的データ解析に代表されるように、近年では数学的な研究に加えて、トポロジーを諸科学・産業へ応用する「応用トポロジー」と
呼ばれる新分野が開拓されています。
- 注2) マテリアルズインフォマティックス
- 計算機性能の飛躍的な発達にともない、これまで蓄積されてきた膨大な材料データに計算科学・数理的な手法を適用することで新物質・新材料を開発する取り組み。従来の試行錯誤的な材料開発とくらべて開発期間や資源の大幅な削減につながることが期待されています。
- 注3) パーシステントホモロジー
- 図形や画像、さらにはより一般の「データの形」をマルチスケールで特徴付ける数学的手法。位相的データ解析と呼ばれるトポロジーを応用したデータ
解析手法の1つです。その起源は19世紀フランスの数学者ポアンカレによって考案されたホモロジーにあり、21世紀になってデータ解析への応用の可能性を
指摘され新たな展開を迎えています。現在、数学研究のみならず諸科学への応用研究が急速に進められています。
- 注4) 分子動力学法
- 古典力学に基づいて、多数の原子の運動方程式を数値的に解き、材料物性を評価する方法。実験や量子力学に基づいて決められる原子間相互作用を与え
る事で化学的性質を表現する事が出来ます。また、実験とつじつまがあうような妥当な原子配置を推定する際に役立ちます。本研究ではガラスの原子配置を求め
る際に使用しています。
- 注5) 第一シャープ回折ピーク(FSDP)
- ガラス構造から得られるX線あるいは中性子散乱プロファイルで低散乱角側(つまり1番目)に出現するシャープな回折ピーク。プロファイルの低散乱角側にあることから、実空間の構造としては比較的長い距離に対応し、ガラスの中距離構造と関係があると言われています。
<論文情報>
| タイトル |
“Hierarchical structures of amorphous solids characterized by persistent homology” |
| 著者名 |
Yasuaki Hiraoka, Takenobu Nakamura, Akihiko Hirata, Emerson G. Escolar, Kaname Matsue, and Yasumasa Nishiura |
| 掲載誌 |
Proceedings of the National Academy of Sciences |




0 Comments:
コメントを投稿
<< Home