追記:
3つの平均
「相加相乗平均の関係」を視覚的に理解する!
追記20190225
無料で使える数学アプリ、GeoGebra スライダーの使い方と教材共有方法
__________________________
3つの平均
3種類の“平均”を紹介します(相加平均・相乗平均・調和平均)
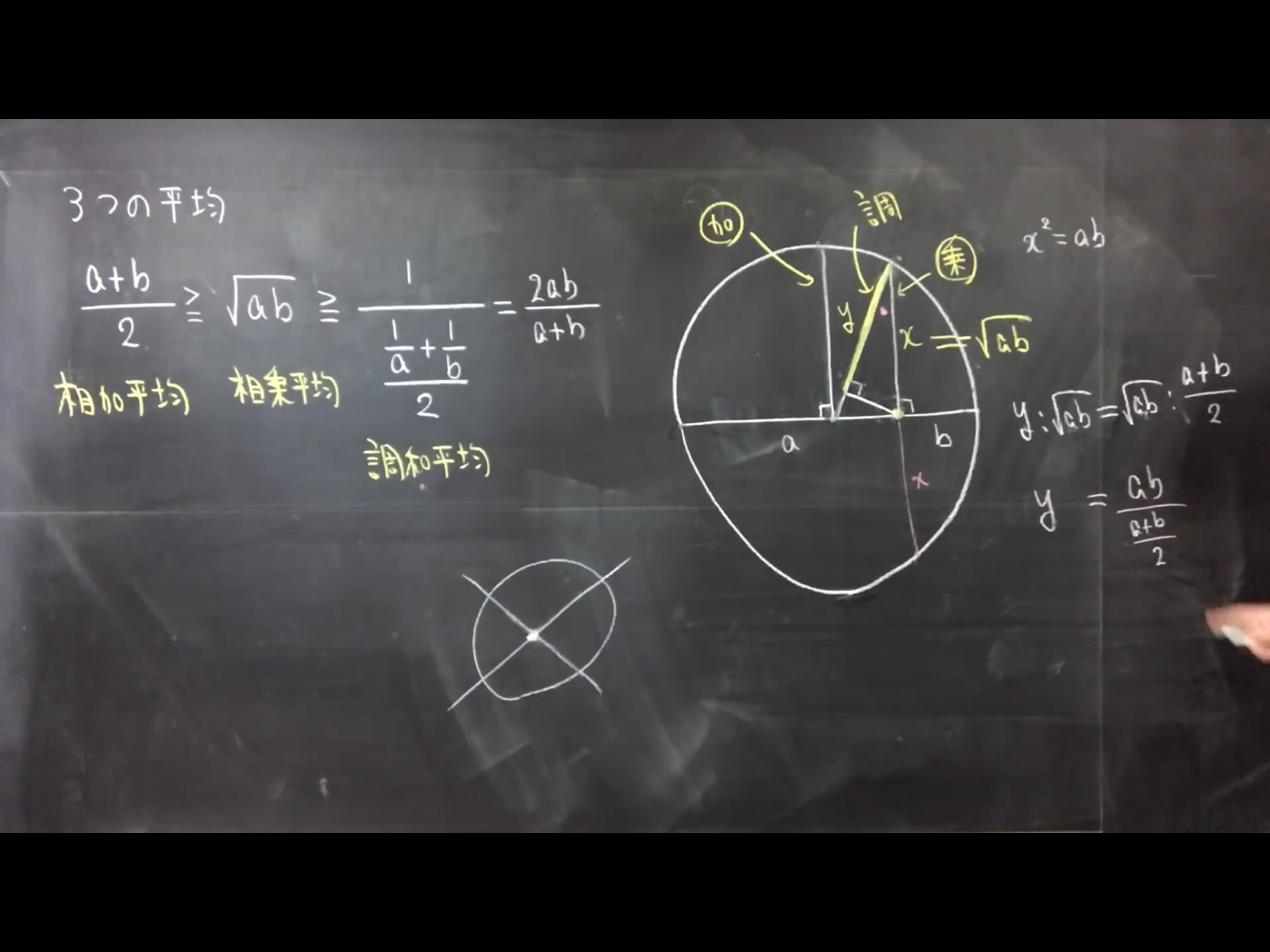
__
7:30
https://ja.wikipedia.org/wiki/%E6%96%B9%E3%81%B9%E3%81%8D%E3%81%AE%E5%AE%9A%E7%90%86
が成り立つ。
が成り立つ。
______
方べきの定理は以下のデカルトによるルートの意味づけと関連して重要
これがなければ座標、図形そのものが代数学的裏付けを持たず無効になりかねない
○ ○
○ | ○
○ √a ○
○___|______○
1 a
=単位線分
これがなければ座標、図形そのものが代数学的裏付けを持たず無効になりかねない
○ ○
○ | ○
○ √a ○
○___|______○
1 a
=単位線分
参考:
デカルトによる量の次元の統一
http://nam-students.blogspot.jp/2012/10/blog-post_16.html
[平方根の抽出]
「…GH[図]の平方根を出さねばならぬとすれば、それと一直線上に単位であるFGを加え、FHを点Kで二等分して、Kを中心とする円FIHを描き、点Gか らFHと直角にIまで立てる。GIは求める根である。立方根その他についてはあとで述べる方が都合がいいから、いまは何も言わないでおく。」
(「幾何学」邦訳『デカルト著作集1』4頁より)
___________________
ただし、このデカルトの説明だけでは初学者にはわからないかもしれない。それは以下の書籍で紹介されているユークリッド第二巻の証明が前提になっているのに、その説明が自明なものだとして省略されているからだ。
以下、 日本の数学西洋の数学―比較数学史の試み (中公新書) ... より
「量の次元の統一の要求」28−29頁
D
|
x
|
A_____B___C
a b
x^2 = ab の幾何学的解法
AB=a,BC=b として、AC=a+bを直径とする半円を描き、
Bに垂線を立てて半円との交点をDとすると、BDが求める長さ x
である。
このことは △ABDと△DBCとが相似となることから、
a:x= x : b すなわち x^2=ab
として証明される。
ただし『原論』第2巻では、まだ相似の理論が示されていないので、
この定理も第2巻の定理を使って別の形で証明されている。
(日本の数学西洋の数学―比較数学史の試み (中公新書 ): 村田全 29頁)
代数学と幾何学の邂逅
http://hooktail.sub.jp/algebra/Descartes/
…デカルト以前の数学者にとって,  が辺の長さを表わす場合,
が辺の長さを表わす場合, 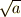 は幾何学的意味を持ちませんでした.『二乗したら辺の長さになる』ような幾何学的量は存在しないからです.ところが,デカルトは次の図を描き,
は幾何学的意味を持ちませんでした.『二乗したら辺の長さになる』ような幾何学的量は存在しないからです.ところが,デカルトは次の図を描き,  と
と 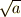 のどちらも単に辺の長さを表わす例を示しました.
のどちらも単に辺の長さを表わす例を示しました.
 が辺の長さを表わす場合,
が辺の長さを表わす場合, 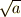 は幾何学的意味を持ちませんでした.『二乗したら辺の長さになる』ような幾何学的量は存在しないからです.ところが,デカルトは次の図を描き,
は幾何学的意味を持ちませんでした.『二乗したら辺の長さになる』ような幾何学的量は存在しないからです.ところが,デカルトは次の図を描き,  と
と 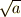 のどちらも単に辺の長さを表わす例を示しました.
のどちらも単に辺の長さを表わす例を示しました.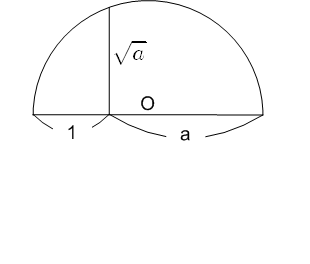
○ ○
○ √a ○
○ | ○
○___|_____○
1 a
単位線分
ここから,直径 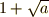 の円を描いて同じ操作を繰り返していくことも可能ですから,結局
の円を描いて同じ操作を繰り返していくことも可能ですから,結局 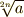 は全て辺の長さとして作図可能になります.これらの図は,デカルトの書いた『 幾何学 』(原題は
は全て辺の長さとして作図可能になります.これらの図は,デカルトの書いた『 幾何学 』(原題は 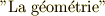 )に出ているものです.
)に出ているものです.
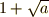 の円を描いて同じ操作を繰り返していくことも可能ですから,結局
の円を描いて同じ操作を繰り返していくことも可能ですから,結局 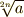 は全て辺の長さとして作図可能になります.これらの図は,デカルトの書いた『 幾何学 』(原題は
は全て辺の長さとして作図可能になります.これらの図は,デカルトの書いた『 幾何学 』(原題は 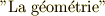 )に出ているものです.
)に出ているものです.代数学と幾何学の邂逅
代数的演算と幾何的演算の橋渡しがされた歴史を紹介します.
フェルマーの幾何学
フェルマーの定理などで有名なフランスの数学者ピエール・ド・フェルマー(  )は,古代ギリシャの数学者アポロニウス(
)は,古代ギリシャの数学者アポロニウス( 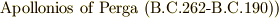 の著した『 円錐曲線論 』(原題は
の著した『 円錐曲線論 』(原題は 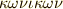 )を研究し,図形を方程式で表現することを始めた最初の数学者です.それまでは,数式の計算と図形の問題は全く別々のものだと考えられていましたので,これは非常に画期的な手法でした.古代バビロニアや古代ギリシャでも,限定的に幾何学の計算に代数学を応用することはありましたが,例えば面積や体積を
)を研究し,図形を方程式で表現することを始めた最初の数学者です.それまでは,数式の計算と図形の問題は全く別々のものだと考えられていましたので,これは非常に画期的な手法でした.古代バビロニアや古代ギリシャでも,限定的に幾何学の計算に代数学を応用することはありましたが,例えば面積や体積を 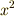 や
や 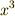 に対応させて方程式を解くといった程度のもので,このレベルを越えることはありませんでした.座標という概念や,より一般的な曲線や軌跡の表現にも代数方程式を使ったのはフェルマーの功績です.
に対応させて方程式を解くといった程度のもので,このレベルを越えることはありませんでした.座標という概念や,より一般的な曲線や軌跡の表現にも代数方程式を使ったのはフェルマーの功績です.
 )は,古代ギリシャの数学者アポロニウス(
)は,古代ギリシャの数学者アポロニウス( 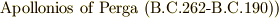 の著した『 円錐曲線論 』(原題は
の著した『 円錐曲線論 』(原題は 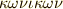 )を研究し,図形を方程式で表現することを始めた最初の数学者です.それまでは,数式の計算と図形の問題は全く別々のものだと考えられていましたので,これは非常に画期的な手法でした.古代バビロニアや古代ギリシャでも,限定的に幾何学の計算に代数学を応用することはありましたが,例えば面積や体積を
)を研究し,図形を方程式で表現することを始めた最初の数学者です.それまでは,数式の計算と図形の問題は全く別々のものだと考えられていましたので,これは非常に画期的な手法でした.古代バビロニアや古代ギリシャでも,限定的に幾何学の計算に代数学を応用することはありましたが,例えば面積や体積を 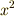 や
や 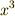 に対応させて方程式を解くといった程度のもので,このレベルを越えることはありませんでした.座標という概念や,より一般的な曲線や軌跡の表現にも代数方程式を使ったのはフェルマーの功績です.
に対応させて方程式を解くといった程度のもので,このレベルを越えることはありませんでした.座標という概念や,より一般的な曲線や軌跡の表現にも代数方程式を使ったのはフェルマーの功績です.
(本職の数学者ではなかったフェルマー)
フェルマーは,座標系を設定するのに,原点と,原点を通る軸を一本定め,平面上の一点から,その軸へ引いた線分の長さ(図中の 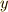 )と,原点から線分の足までの長さ(図中の
)と,原点から線分の足までの長さ(図中の  )を座標
)を座標 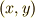 と定義しました.これは今日,斜交座標と呼ばれているもので,今日の私達から見ると少し変わった座標の取り方です.
と定義しました.これは今日,斜交座標と呼ばれているもので,今日の私達から見ると少し変わった座標の取り方です.
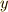 )と,原点から線分の足までの長さ(図中の
)と,原点から線分の足までの長さ(図中の  )を座標
)を座標 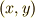 と定義しました.これは今日,斜交座標と呼ばれているもので,今日の私達から見ると少し変わった座標の取り方です.
と定義しました.これは今日,斜交座標と呼ばれているもので,今日の私達から見ると少し変わった座標の取り方です.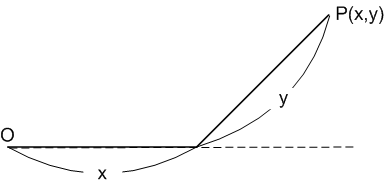
フェルマーはこの座標を用いて,線分の方程式と円錐曲線を代数方程式として表わすことに成功しました.また逆に,方程式を満たす座標の軌跡をその方程式の表わす図形と対応させ,曲線の分類を行うという,のちに解析幾何学へと発展する研究を行いました.解析幾何学への道を拓いたという点で,フェルマーの功績は非常に大きなものがありますが,フェルマーは古代ギリシャ人同様, 方程式の同次性 にこだわり,異なる次数の項を含む方程式を幾何学の文脈で認めることを潔しとしませんでした.
例えば,文字  が辺の長さを表わす場合,二次の項
が辺の長さを表わす場合,二次の項 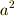 は面積,三次の項
は面積,三次の項 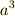 は体積を表わすと考えることができます.(簡単な代数方程式に,面積や体積などの図形的イメージを対応させることは古代バビロニアでも既に行われていました. 平方完成の図形的イメージ を参照してみてください.) 例えば,
は体積を表わすと考えることができます.(簡単な代数方程式に,面積や体積などの図形的イメージを対応させることは古代バビロニアでも既に行われていました. 平方完成の図形的イメージ を参照してみてください.) 例えば, 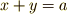 は『辺の長さの和
は『辺の長さの和 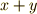 が,長さ
が,長さ  に等しい』ことを示し,
に等しい』ことを示し, 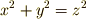 は『面積の和
は『面積の和 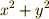 が面積
が面積 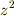 に等しい』ことを意味するといった具合です.しかし,この視点に固執すると,例えば
に等しい』ことを意味するといった具合です.しかし,この視点に固執すると,例えば 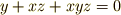 という式は,『長さと面積と体積を足す(!?)』という幾何学的にナンセンスな主張を表わしていることになり,無意味な式だと考えざるをえません.実は,次節に見るように,次数の違う項の混じった方程式が,幾何学的に無意味だというわけではないのですが,フェルマーも古代ギリシャ以来の"同次式の呪縛"に囚われていましたので,代数的演算を自由自在に幾何学的演算に役立てるには至りませんでした.
という式は,『長さと面積と体積を足す(!?)』という幾何学的にナンセンスな主張を表わしていることになり,無意味な式だと考えざるをえません.実は,次節に見るように,次数の違う項の混じった方程式が,幾何学的に無意味だというわけではないのですが,フェルマーも古代ギリシャ以来の"同次式の呪縛"に囚われていましたので,代数的演算を自由自在に幾何学的演算に役立てるには至りませんでした.
 が辺の長さを表わす場合,二次の項
が辺の長さを表わす場合,二次の項 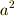 は面積,三次の項
は面積,三次の項 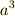 は体積を表わすと考えることができます.(簡単な代数方程式に,面積や体積などの図形的イメージを対応させることは古代バビロニアでも既に行われていました. 平方完成の図形的イメージ を参照してみてください.) 例えば,
は体積を表わすと考えることができます.(簡単な代数方程式に,面積や体積などの図形的イメージを対応させることは古代バビロニアでも既に行われていました. 平方完成の図形的イメージ を参照してみてください.) 例えば, 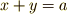 は『辺の長さの和
は『辺の長さの和 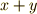 が,長さ
が,長さ  に等しい』ことを示し,
に等しい』ことを示し, 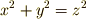 は『面積の和
は『面積の和 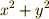 が面積
が面積 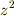 に等しい』ことを意味するといった具合です.しかし,この視点に固執すると,例えば
に等しい』ことを意味するといった具合です.しかし,この視点に固執すると,例えば 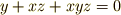 という式は,『長さと面積と体積を足す(!?)』という幾何学的にナンセンスな主張を表わしていることになり,無意味な式だと考えざるをえません.実は,次節に見るように,次数の違う項の混じった方程式が,幾何学的に無意味だというわけではないのですが,フェルマーも古代ギリシャ以来の"同次式の呪縛"に囚われていましたので,代数的演算を自由自在に幾何学的演算に役立てるには至りませんでした.
という式は,『長さと面積と体積を足す(!?)』という幾何学的にナンセンスな主張を表わしていることになり,無意味な式だと考えざるをえません.実は,次節に見るように,次数の違う項の混じった方程式が,幾何学的に無意味だというわけではないのですが,フェルマーも古代ギリシャ以来の"同次式の呪縛"に囚われていましたので,代数的演算を自由自在に幾何学的演算に役立てるには至りませんでした.| [*] | そういえば,有名なフェルマーの大定理に出てくる式 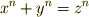 も同次式ですね! も同次式ですね! |
デカルトの幾何学
古代ギリシャ以来,フェルマーも含めて,幾何学における式は『同次式でなければ意味がない』と考えられていたわけですが,この呪縛を解いたのがデカルト( 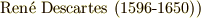 です.デカルトは幾何学的文脈においてでさえ,辺,面積,体積などの区別を問題にせず,数そのものを研究しました.これは計算における大きな視点の転換だったに違いありません.
です.デカルトは幾何学的文脈においてでさえ,辺,面積,体積などの区別を問題にせず,数そのものを研究しました.これは計算における大きな視点の転換だったに違いありません.
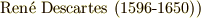 です.デカルトは幾何学的文脈においてでさえ,辺,面積,体積などの区別を問題にせず,数そのものを研究しました.これは計算における大きな視点の転換だったに違いありません.
です.デカルトは幾何学的文脈においてでさえ,辺,面積,体積などの区別を問題にせず,数そのものを研究しました.これは計算における大きな視点の転換だったに違いありません.
(『我思う故に我あり』(cogito ergo sum)の一文はあまりにも有名)
例を二つ挙げましょう.デカルト以前の数学者にとって,  と
と  が辺の長さを表わす場合,
が辺の長さを表わす場合, 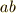 は
は  ,
,  を辺の長さとする長方形の面積を表わす量でした.これに対しデカルトは,
を辺の長さとする長方形の面積を表わす量でした.これに対しデカルトは, 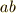 も単にある数を表すだけであり,次の比例式の第四項を表わすに過ぎないと考えたのです.
も単にある数を表すだけであり,次の比例式の第四項を表わすに過ぎないと考えたのです.
 と
と  が辺の長さを表わす場合,
が辺の長さを表わす場合, 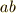 は
は  ,
,  を辺の長さとする長方形の面積を表わす量でした.これに対しデカルトは,
を辺の長さとする長方形の面積を表わす量でした.これに対しデカルトは, 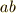 も単にある数を表すだけであり,次の比例式の第四項を表わすに過ぎないと考えたのです.
も単にある数を表すだけであり,次の比例式の第四項を表わすに過ぎないと考えたのです.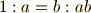
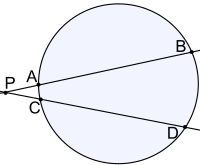
この式の第四項が必ずしも面積を意味しているのではないことは,次の図から分かります.図中, 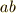 も
も  や
や  同様,辺の長さを表わしています.(線分
同様,辺の長さを表わしています.(線分 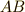 と線分
と線分 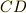 が平行なので,
が平行なので, 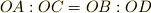 が成り立つのは大丈夫ですね.)
が成り立つのは大丈夫ですね.) 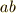 に対してさらに同様の図を描けば,今度は三次の項で辺の長さを表わすものが求められます.この操作は無限回繰り返せますので,結局,辺の長さであっても
に対してさらに同様の図を描けば,今度は三次の項で辺の長さを表わすものが求められます.この操作は無限回繰り返せますので,結局,辺の長さであっても 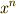 の形の項は幾らでも存在しており,これらの和や差も幾何学的に無意味ではなくなります.
の形の項は幾らでも存在しており,これらの和や差も幾何学的に無意味ではなくなります.
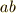 も
も  や
や  同様,辺の長さを表わしています.(線分
同様,辺の長さを表わしています.(線分 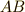 と線分
と線分 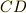 が平行なので,
が平行なので, 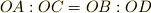 が成り立つのは大丈夫ですね.)
が成り立つのは大丈夫ですね.) 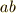 に対してさらに同様の図を描けば,今度は三次の項で辺の長さを表わすものが求められます.この操作は無限回繰り返せますので,結局,辺の長さであっても
に対してさらに同様の図を描けば,今度は三次の項で辺の長さを表わすものが求められます.この操作は無限回繰り返せますので,結局,辺の長さであっても 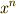 の形の項は幾らでも存在しており,これらの和や差も幾何学的に無意味ではなくなります.
の形の項は幾らでも存在しており,これらの和や差も幾何学的に無意味ではなくなります.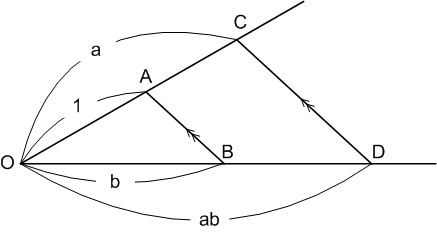
(図1)
同様に,デカルト以前の数学者にとって,  が辺の長さを表わす場合,
が辺の長さを表わす場合, 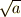 は幾何学的意味を持ちませんでした.『二乗したら辺の長さになる』ような幾何学的量は存在しないからです.ところが,デカルトは次の図を描き,
は幾何学的意味を持ちませんでした.『二乗したら辺の長さになる』ような幾何学的量は存在しないからです.ところが,デカルトは次の図を描き,  と
と 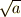 のどちらも単に辺の長さを表わす例を示しました.
のどちらも単に辺の長さを表わす例を示しました.
 が辺の長さを表わす場合,
が辺の長さを表わす場合, 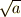 は幾何学的意味を持ちませんでした.『二乗したら辺の長さになる』ような幾何学的量は存在しないからです.ところが,デカルトは次の図を描き,
は幾何学的意味を持ちませんでした.『二乗したら辺の長さになる』ような幾何学的量は存在しないからです.ところが,デカルトは次の図を描き,  と
と 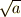 のどちらも単に辺の長さを表わす例を示しました.
のどちらも単に辺の長さを表わす例を示しました.
(図2)
ここから,直径 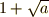 の円を描いて同じ操作を繰り返していくことも可能ですから,結局
の円を描いて同じ操作を繰り返していくことも可能ですから,結局 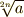 は全て辺の長さとして作図可能になります.これらの図は,デカルトの書いた『 幾何学 』(原題は
は全て辺の長さとして作図可能になります.これらの図は,デカルトの書いた『 幾何学 』(原題は 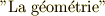 )に出ているものです.
)に出ているものです.
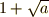 の円を描いて同じ操作を繰り返していくことも可能ですから,結局
の円を描いて同じ操作を繰り返していくことも可能ですから,結局 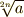 は全て辺の長さとして作図可能になります.これらの図は,デカルトの書いた『 幾何学 』(原題は
は全て辺の長さとして作図可能になります.これらの図は,デカルトの書いた『 幾何学 』(原題は 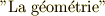 )に出ているものです.
)に出ているものです.
上の二例により,線分の長さの  乗や
乗や 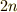 乗根もやはり線分の長さを表わす(ことができる)ことがわかりました.ここに至って,次数が違う文字同士の計算や,高次の代数方程式でも,幾何学的意味を失わずに文字計算を行える道が拓けました.これ以後,代数的演算と幾何学的演算の対応はより自由になり,代数学の成果を幾何学に存分に応用できるようになります.今の私達にとっては何でもないことのように思えますが,幾何学的方程式が『同次式の呪縛』から逃れるのに数千年の時間を要したことに思いを致してみましょう.
乗根もやはり線分の長さを表わす(ことができる)ことがわかりました.ここに至って,次数が違う文字同士の計算や,高次の代数方程式でも,幾何学的意味を失わずに文字計算を行える道が拓けました.これ以後,代数的演算と幾何学的演算の対応はより自由になり,代数学の成果を幾何学に存分に応用できるようになります.今の私達にとっては何でもないことのように思えますが,幾何学的方程式が『同次式の呪縛』から逃れるのに数千年の時間を要したことに思いを致してみましょう.
 乗や
乗や 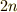 乗根もやはり線分の長さを表わす(ことができる)ことがわかりました.ここに至って,次数が違う文字同士の計算や,高次の代数方程式でも,幾何学的意味を失わずに文字計算を行える道が拓けました.これ以後,代数的演算と幾何学的演算の対応はより自由になり,代数学の成果を幾何学に存分に応用できるようになります.今の私達にとっては何でもないことのように思えますが,幾何学的方程式が『同次式の呪縛』から逃れるのに数千年の時間を要したことに思いを致してみましょう.
乗根もやはり線分の長さを表わす(ことができる)ことがわかりました.ここに至って,次数が違う文字同士の計算や,高次の代数方程式でも,幾何学的意味を失わずに文字計算を行える道が拓けました.これ以後,代数的演算と幾何学的演算の対応はより自由になり,代数学の成果を幾何学に存分に応用できるようになります.今の私達にとっては何でもないことのように思えますが,幾何学的方程式が『同次式の呪縛』から逃れるのに数千年の時間を要したことに思いを致してみましょう.| [†] | ここで例示した二つの図は,『定規とコンパスだけで作図できる図形にはどのようなものがあるか?』という問題に深く関係します.例えば, 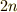 乗根で表わされる長さが作図可能なことは例に見ましたが, 乗根で表わされる長さが作図可能なことは例に見ましたが, 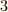 乗根は作図できないのでしょうか?この問題に取り組むには少し準備が要ります.いずれ体論で,この作図可能性の問題を取り上げる予定です. 乗根は作図できないのでしょうか?この問題に取り組むには少し準備が要ります.いずれ体論で,この作図可能性の問題を取り上げる予定です. |
練習問題
定規とコンパスで,正五角形を作図する方法を考えてみましょう.
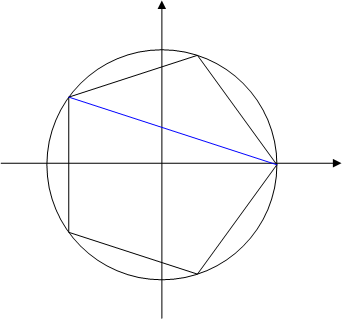
(ヒント:この方法をいきなり思いつくのは大変ですが,円の半径を 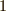 として解析的に辺や対角線の長さを計算してみると,一辺の長さは
として解析的に辺や対角線の長さを計算してみると,一辺の長さは 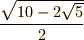 ,図中青線で表わされる対角線の長さは
,図中青線で表わされる対角線の長さは 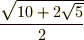 と分かります.根号・和・差は,どんなに大変でも必ずコンパスと定規で描けるはずです.まずはピタゴラスの定理を使って,辺の長さが
と分かります.根号・和・差は,どんなに大変でも必ずコンパスと定規で描けるはずです.まずはピタゴラスの定理を使って,辺の長さが 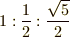 の直角三角形を描いてみましょう.)
の直角三角形を描いてみましょう.)
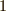 として解析的に辺や対角線の長さを計算してみると,一辺の長さは
として解析的に辺や対角線の長さを計算してみると,一辺の長さは 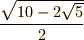 ,図中青線で表わされる対角線の長さは
,図中青線で表わされる対角線の長さは 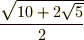 と分かります.根号・和・差は,どんなに大変でも必ずコンパスと定規で描けるはずです.まずはピタゴラスの定理を使って,辺の長さが
と分かります.根号・和・差は,どんなに大変でも必ずコンパスと定規で描けるはずです.まずはピタゴラスの定理を使って,辺の長さが 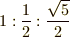 の直角三角形を描いてみましょう.)
の直角三角形を描いてみましょう.)
正五角形の作図法は古代ギリシャで既にユークリッド( 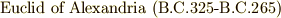 )やトレミー(
)やトレミー( 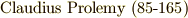 )によって知られていました.正五角形の辺と対角線の長さの比は,黄金比と呼ばれる値
)によって知られていました.正五角形の辺と対角線の長さの比は,黄金比と呼ばれる値 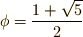 になります.
になります.
 )やトレミー(
)やトレミー(  )によって知られていました.正五角形の辺と対角線の長さの比は,黄金比と呼ばれる値
)によって知られていました.正五角形の辺と対角線の長さの比は,黄金比と呼ばれる値 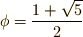 になります.
になります.





8 Comments:
1テストの平均点
2会社の成長率
3スピード
デカルト以前では,aが線分であると考えると√aは意味を持っていなかった。しかし,デカルトにとっては,1とaを表す線分が与えられた場合√aを表す線分は図3の作図で与えられる線分の長さとして考えることができる。
二重の円が描ける
一という単位の設定で1つの円になる
方べきの定理は以下のデカルトによるルートの意味づけと関連して重要
これがなければ座標、図形そのものが代数学的裏付けを持たず無効になりかねない
○ ○
○ √a ○
○ | ○
○___|_____○
1 a
=単位線分
方べきの定理は以下のデカルトによるルートの意味づけと関連して重要
これがなければ座標、図形そのものが代数学的裏付けを持たず無効になりかねない
○| ○
○ √a ○
○ | ○
○___|_____○
1 a
=単位線分
方べきの定理は以下のデカルトによるルートの意味づけと関連して重要
これがなければ座標、図形そのものが代数学的裏付けを持たず無効になりかねない
○ ○
○ | ○
○ √a ○
○___|______○
1 a
=単位線分
正規分布のおもちゃ【GALTON BOARD】
https://youtu.be/lpMLo9z_Xjw
https://vt.tiktok.com/ZSeBhYyGe/
コメントを投稿
<< Home