渋滞の原因を数学的に分析すると自動運転カーの登場で移動にかかる時間が減る理屈がよくわかる
自動運転カー(自律走行車)が普及すると、交差点での無駄がなくなり待ち時間解消によって効率化が進むと考えられてます。それだけでなく、道路上の自動車が増え過密化することで全体のペースが大きく下がるという現象が解消されたり、理想的な道路選択をサポートすることで、交通渋滞が劇的に解消するということがStanford Artificial Intelligence Laboratory(SAIL)の数学的な検証によって示されています。
Altruistic Autonomy: Beating Congestion on Shared Roads | SAIL Blog
http://ai.stanford.edu/blog/altruistic-autonomy/
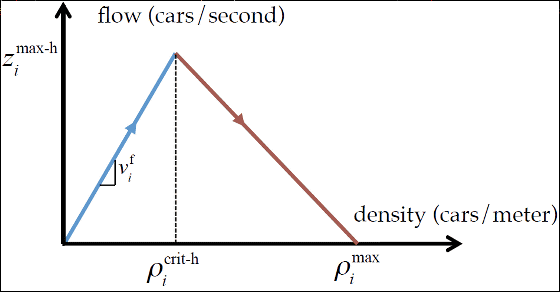
以下のグラフは理想的な道路交通条件を研究するFundamental Diagram of Traffic(FDT)において作成された道路交通状態を表すグラフで、縦軸に道路上のある地点を1秒間に通過する自動車の数(flow)、横軸に1メートルあたりに存在する自動車の数(density)をプロットしたもの(FDT1)です。グラフが山のような形状を持ち、右肩上がりの青色部分と右肩下がりの赤い部分になるのが特徴です。
上記FDT1の内容を説明すると、原点は道路上に自動車が0台の状態で、周りを走る自動車がないため最高速度でスイスイ快適に走ることが可能です。自動車の数が増えたとしても十分なスペースがある青色部分の間は全車が最高速度で快適に走ることができるので、自動車の台数(densityと等価)に比例してflowも高まっていきます。
しかし、自動車が走行する場合、一般的に前を走る自動車との間に最低2秒分の距離をあける必要があります。これは前方の車両が急ブレーキをかけても事故を起こさないように最低限必要となる車間距離で、自動車の数が増えてdensityが増えるとすべての自動車が2秒間隔では走れなくなるポイント(飽和点)に到達します。これが上記グラフの山の頂上であり、車間距離で2秒分を保つためには道路上の自動車は台数が増えるとともにスピードを落とさざるを得なくなります。そのため、densityが飽和点を超えるとflowは右肩下がりの状態(赤色部分)になってしまいます。
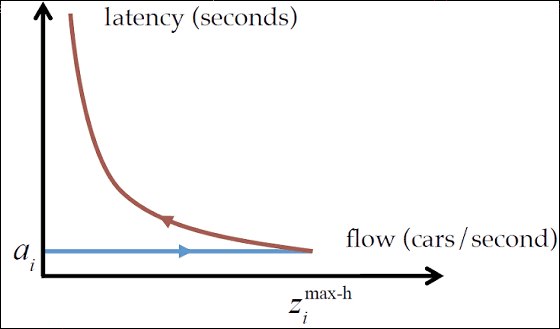
以下のグラフは縦軸に道路上のある地点から別の地点移動するのにかかる待ち時間(latency)、横軸にflowをとったグラフ(FDT2)。青色部分では、前車が最高速で走行できるためlatencyは一定です。ただし、飽和点に到達すると速度が低下することでlatencyは上昇してしまいます。なお、飽和点以降の赤色部分はflowも低下していくので、グラフは双曲線状になります。つまり、飽和点を境として自動車の台数が増えるほど、目的地への到達時間が長くなることがわかります。
現実世界では自動車は全車が一定速度で走るわけもなく、車間距離もまちまちであるため上記2つのグラフは理想状態の理論値ですが、自動車の数が増えるとある時点で急に目的地まで到達するのにかかる時間が長くなり始めるという特徴は理解しやすいといえます。
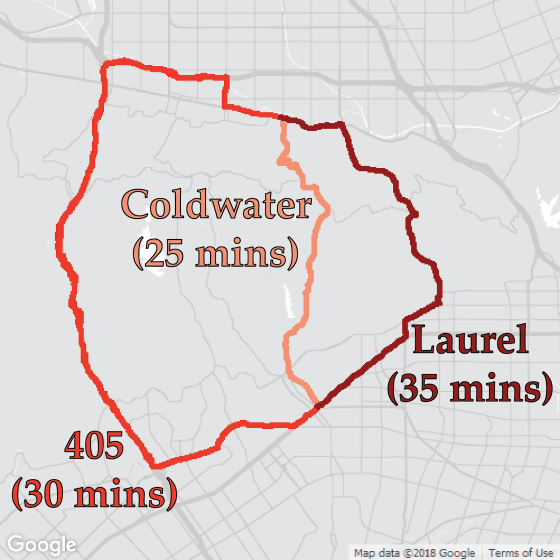
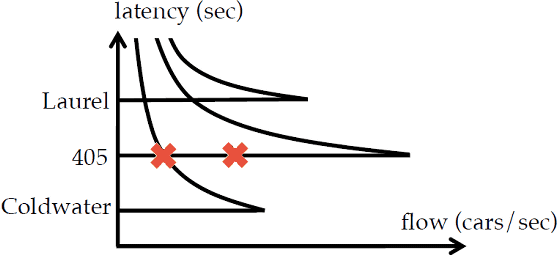
さらに、現実の世界では「利己主義的」な人間の特性のため、道路交通にはより複雑な力学が働くことになります。ロサンゼルスのBeverly Hillsからthe Valleyに自動車で移動する場合を検討してみます。経路は3通りあり、最短経路の「Coldwater」なら25分、「ハイウェイ405号線」なら30分、距離の長い「Laurel」なら35分かかります。
もちろんコースごとに渋滞しやすい時間帯などもあるため一概にはいえませんが、数分の時短のためにColdwaterを選択するドライバーは多いはずです。しかし、このように考えるのはみな同じで、多くのドライバーがColdwaterを選択するせいでColdwaterのdensityが高まり、飽和点を超えてしまい結果的に移動時間が長くなる……ということが日常的に起こっています。ここで重要なことは、交通量の多いColdwaterで移動時間が伸びたことが社会的な損失として規模が大きいということ。もしもLaurelを選ぶドライバーがもう少し多ければ、Coldwaterで失われる全体的な経済的損失は小さく済み、結果としてLaurelを走行するドライバーの犠牲の下、より大きな利益が生み出されたかもしれないというわけです。このような道路上でのコモンズの悲劇類似の現象が起こっています。
どの道を選択するのかについて、ドライバーは他のドライバーの「戦略」も検討して決定します。仮に、どの道を選んだとしても同じ時間かかるならば他の道に切り替えようというインセンティブは働かなくなり、ナッシュ均衡が発生します。当然ながらナッシュ均衡が生じる条件は1つではなく、さまざまな状態があり得ます。
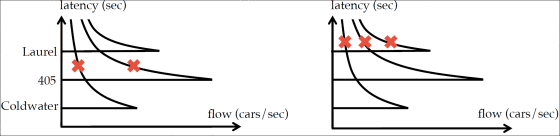
ナッシュ均衡の状態を図示したのが以下のグラフ。3路線ごとにFDT2のグラフをプロットしており、図の中の「×」は現実の道路状況を示してます。両方ともにナッシュ均衡が生じた状態ですが、左の図の方が縦軸のlatencyの値が小さいので、目的地までの到着時間は短いことになります。ここで重要なのは、両方のグラフが同じ台数の自動車が走行している場合についてのものだということ。つまり、同じ台数の自動車を移動させる場合でも、ナッシュ均衡が起こる場所次第で目的地到着までにかかる時間が長くなったり短くなったりするということです。
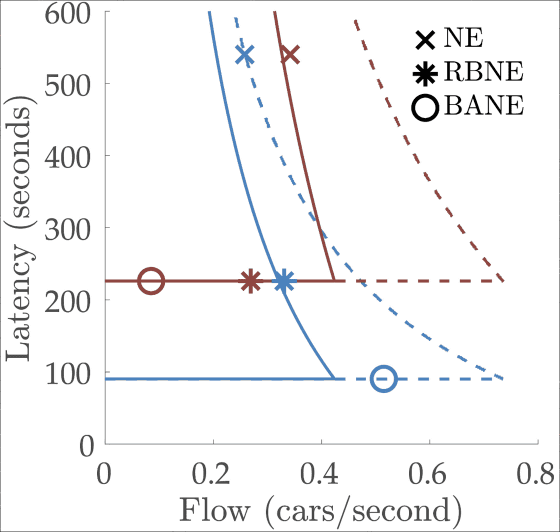
上記のグラフと同じ条件で、さらにlatencyが短くなる状態が以下のグラフ。このグラフの状態では405号線は十分な空きがある状態で、別の自動車が加わったとしても最高速で走行できる状況です。すぐに飽和してしまうColdwaterではなくキャパの大きな405号線を走るドライバーが多いほど、結果として待ち時間は短くなるというわけです。
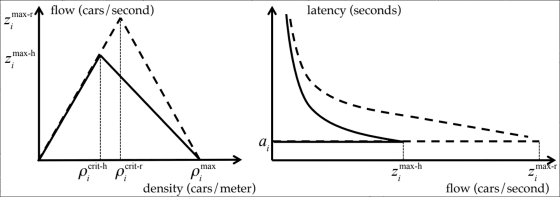
以上の通り走行できる最高スピードは道路の混み具合に関わってくること、車間距離を維持するための時間が重要であることは明らかです。この点、人間は2秒分の車間距離が必要ですが、自動運転カー(自律走行カー)であれば、より短い車間距離での走行が可能です。技術が高まれば、1秒未満の車間距離で安定走行できるようになるのはほぼ確実です。
仮に、道路上のすべての自動車が自動運転カーだと仮定すると、FDT1とFDT2のグラフは、以下のグラフの破線のように大きく変化します。最高速度を維持して快適に走れる台数が増え、飽和点に達するまでの限界点が伸びるというわけです。
まったく同じナッシュ均衡状態の道路でも、走行する自動車の一般車と自動運転カーの比率によって、スピードダウンへの耐性(堅牢性)に差は生まれます。たとえは、以下の2つのFDT2グラフは、一般車と自動運転カーがそれぞれ同じ台数混ざって走行する状態で、latencyも同じ状態なので、目的地までの到着時間は同じです。しかし、右のグラフはただでさえキャパの大きい405号線により多くの自動運転カーが集まることで、飽和点までの限界をより広げているため、latency(移動時間)を上げることなく多くの自動車を追加できることになり、スピードダウンまでの耐性が高いといえます。つまり、右の状況の方が堅牢性が高く、「渋滞に強い(渋滞しにくい)」といえます
SAILの研究者は、あるナッシュ均衡状態(NE)を、latencyを最も下げる理想的なナッシュ均衡状態(BANE)と堅牢性が最も大きな状態(RBNE)という2つの条件に誘導することで、latencyを大幅に下げられることをシミュレーションで確認したそうです。
以上の通り、一般車であれ自動運転カーであれ、また両者が混在する条件であれ、各道路に適切に自動車を分配することで、全体として到着時間が短くなるようなベストな条件を作り出すことは可能です。理想状態を作り出す妨げになっているのは人間が持つ利己主義的な考えですが、自動運転カーが普及して、道路を走る全ての車両が連携するようなシステムを作り上げることで、渋滞が少なく経済的な損失の少ない交通事情を作りだすことができるようになるかもしれません。




0 Comments:
コメントを投稿
<< Home