http://mathtrain.jp/mugentouhi ☆
1
___________________/___
| | |16| ... |
| | 1/4 |__|__|
| | | 1/8 |
| 1 |_____|_____|
| | |
| | 1/2 |
| | |
|___________|___________|
_________
全体で1
_______________________
| | |
| | |
| | |
| | 1/4 |
| | |
| | |
| | |
| 1/2 |___________|
| | | |
| | |1/16 |
| | | |
| | 1/8 |_____|
| | | 1|1/62
| | | /|__|
| | |32| ... |
|___________|_____|__|__|
_______________________
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| |___________|
| | | |
| | | |
| | | |
| | |_____|
| | | | |
| | | |__|
| | | | |
|___________|_____|__|__|
___________
全体で3?
/\
/ \
/ \
/ \
/ 1/3 \
/ \
/ \
/______________\
/\///////////////\
/ \///////////// \
/1/9 \/////////// \
/______\///////// \
1/27\///////\/////// \
/__\///// \///// \
/\///\/// \/// \
/__\/__\/______\/______________\
(これはフラクタルだが収束しない。)
________________
参考:
極限>数列の極限と級数
極限
数列の極限と級数
高校数学下8:pp.106-7
極限>数列の極限と級数
↑ S
| /
| /|
| / |
| / |
| / ↓
| ̄-_ / |
|  ̄-__→/ |
P|____|_ ̄-| |
| | /  ̄-_ |
| |/__←___ ̄-|
| /  ̄-_D
| /
_|______________→量
0|
価格
↑
| \ S
| \ _- ̄
| \____→__ _- ̄
| |\ _- ̄
P| | \ _- ̄ |
| |_-\| |
| _- ̄___\ |
|_- ̄ \ ↓
| \ |
| ←_________\|
| \D
_|______________→量
0|
_________
ピラミッドを廻りながら登って行くイメージ。
横から見るか、
上から見るか。
最初のイメージも、巻貝のようにデザインすれば2番目のイメージに近くなる。
_________
☆
高校数学 無限等比級数の収束,発散の条件と証明など
http://mathtrain.jp/mugentouhi
a=0 の場合は全ての項が0 となりつまらない(明らかに0 に収束する)のでこの記事ではa≠0 の場合を考えます。
高校数学で扱う最も簡単な無限級数である無限等比級数について。公式の証明や諸注意などを解説。
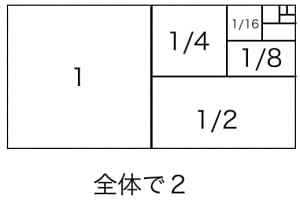
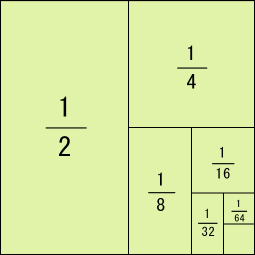
a=1,r=12 の場合を考えてみます。公式より無限級数は11−12=2 に収束します。
 右の図を見れば
右の図を見れば1+12+14+18+⋯=2 は納得できるでしょう。
この図は非常に有名です。無限個の正の数を足しても無限大に発散せず有限の値に収束することがあることがひと目で納得できます。
r=1 の場合は等比数列の和の形が異なるので場合分けをする必要があります。
r=1 のとき,求める無限級数の値はa+a+a+⋯ となり発散。
・r≠1 のとき,無限等比級数の第n 項目までの和をSn とおく:
Sn=a+ar+ar2+⋯+arn−1
これは等比数列の和の公式より簡単に計算できる→等比数列の和の公式の証明といろんな例:
Sn=a−arn1−r
求める無限級数の値はlimn→∞Sn である。
これは,−1<r<1 のときa1−r に収束,
r≤−1,1<r のときに発散する。
注:ここで言う発散とは「収束しない」の意味です。より詳しく言うと,
arn の項が消えます。その結果,等比数列の和の公式よりも無限等比級数の公式の方が綺麗になります!
・「無限級数」という言葉は「無限項の和」を表します。「無限級数の和」という言葉にはやや違和感を感じます(頭痛が痛いみたいな感じ)。
・a1−r に収束する場合について,
1.無限等比級数の値が初項a に比例する
2.公比r が1 に近いほど(絶対値が)大きくなりr→1 で発散する
というのは直感的にも納得できます。
☆
高校数学 無限等比級数の収束,発散の条件と証明など
http://mathtrain.jp/mugentouhi
無限等比級数の収束,発散の条件と証明など
無限等比級数a+ar+ar2+⋯ は
−1<r<1 のとき収束し,その値はa1−r
r≤−1,1≤r のときに発散する。
初項高校数学で扱う最も簡単な無限級数である無限等比級数について。公式の証明や諸注意などを解説。
収束すること
具体例として
この図は非常に有名です。無限個の正の数を足しても無限大に発散せず有限の値に収束することがあることがひと目で納得できます。
無限等比級数の公式の証明
無限級数の値とは有限和の極限のことです。等比数列の和の公式を知っていれば,極限を取るだけで簡単に証明できます。ただし,証明
・・
これは等比数列の和の公式より簡単に計算できる→等比数列の和の公式の証明といろんな例:
求める無限級数の値は
これは,
a>0,r≥1 のとき正の無限大に発散a<0,r≥1 のとき負の無限大に発散r≤−1 のとき振動
諸注意
・極限を取る操作のおかげで・「無限級数」という言葉は「無限項の和」を表します。「無限級数の和」という言葉にはやや違和感を感じます(頭痛が痛いみたいな感じ)。
・
1.無限等比級数の値が初項
2.公比
というのは直感的にも納得できます。
参考:
経済学で出る数学 高校数学からきちんと攻める 2008年 10月号 [雑誌]: 本
http://www.amazon.co.jp/dp/B001HWCR2Y/67,75頁参照





1 Comments:
/\
/ \
/ \
/ \
/ 1/4 \
/ \
/ \
/______________\
/\ /\
/ \ / \
/1/16\ / \
/______\ / \
1/64\ /\ / \
/__\ / \ / \
/\ /\ / \ / \
/__\/__\/______\/______________\
コメントを投稿
<< Home