対角線論法:メモ

https://mathtrain.jp/cantor

B={a∣a∉f(a)}$$ という集合を用いた上記のような証明手法を対角線論法と言います。上の証明を以下のように言い換えると「対角線論法」と呼ばれることが納得できるでしょう。

証明（言い換え）

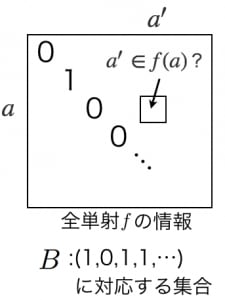
全単射 f$$ が存在すると仮定する。

各行、各列がそれぞれ A$$ の要素に対応した（無限のサイズの）行列を考える。行が a$$，列が a′${}^{}$に対応する部分には a′∈f(a)${}^{}$ なら 1$\mathrm{}$ を格納し，そうでないなら 0$\mathrm{}$ を格納する。

対角成分の 0$\mathrm{}$ と 1$\mathrm{}$ とを反転させたものを並べたベクトル B→$\stackrel{}{}$ に対応する集合を B$$ とする。すると，B→$\stackrel{}{}$ は行列のどの行とも一致しないので，いかなる a∈A$$ に対しても f(a)≠B$$ である。

一方，背理法の仮定より，f$$ は A$$ から 2A${\mathrm{}}^{}$ への全単射なので f(b)=B$$ となる b∈A$$ が存在しなくてはならない。

これは矛盾である。よって，背理法により全単射が存在しないことが証明された。