http://nam-students.blogspot.jp/2016/01/blog-post_26.html
ルベーグ積分
数学において関数の積分はその関数と x 軸の間の図形の面積とみなすことができる。ルベーグ積分(ルベーグせきぶん、Lebesgue integral)とは、より広い種類の関数が積分できるように拡張したものである。ルベーグ積分においては、被積分関数は連続である必要はなく、至るところ不連続でもよいし、関数値として無限大をとることがあってもよい。さらに、関数の定義域も拡張され、測度空間と呼ばれる空間で定義された関数を被積分関数とすることもできる。
このような積分の拡張が必要となった背景には、フーリエ級数などの関数列の極限として表される関数に対して、積分と極限操作が可換となるかどうかをリーマン積分で考えるために非常に繊細な議論が必要だったということがある。この点について、ルベーグ積分では、関数列の極限が被積分関数として適当かどうかを考える必要がなく、積分と極限操作の交換も簡単な十分条件が分かっている。
ルベーグ積分の名前は、数学者のアンリ・ルベーグ(Henri Lebesgue、1875年 - 1941年)に由来している。
概要
積分を厳密なものにしようという動きは、19世紀に始まる。ベルンハルト・リーマンが提案したリーマン積分は大きな前進であった。リーマンは関数の積分を「簡単に計算できる積分」で近似することによって定義した。この定義による積分は、それまで解答が知られていた問題に対して予想通りの結果をもたらしたし、他の問題に対しても新しい結果を与えることになった。
しかし、リーマン積分は関数列の極限との相性が悪く、そのような極限と積分が同時にあらわれるような局面では困難な解析を必要とする場合があった。それに対して、ルベーグ積分においては、積分記号のもとでの極限がより扱いやすくなっている。ルベーグ積分では、リーマンとは異なる形の「簡単に計算できる積分」を考えており、このことがルベーグ積分がリーマン積分よりよく振舞う理由となっている。さらに、ルベーグ積分ではリーマン積分より広い種類の関数に対して積分を定義することが可能になっている。例えば、無理数で 0 を有理数で 1 をとる関数(ディリクレの関数)はリーマン積分では積分が定義されないが、ルベーグ積分では積分できる。
ルベーグ積分の構成
以下ルベーグ積分のよく知られた構成法を示す。この方法は二つの章に分けられる。
- 可測集合と測度
- 可測関数と積分
この二つの章の内容は、直感的には円柱や三角柱の体積を計算する前に底面積を計算し、ついで、高さをかけるという作業に似ている。すべての平面図形の面積を定義するのが最初の章であり、その図形を底面とする複雑な立体の体積を計算するのが第二の章である。
測度論
当初、測度論は線分、平面図形、立体などの長さ、面積、体積などの精密な解析のために考え出されたものである。特に 実数全体の集合R の部分集合について、その部分集合の長さとは何か、という問いに対して整然とした解答を与えるものであった。 集合論の発展によって、自然な加法性を持ち、平行移動不変になるように、実数体R のすべての部分集合に長さを定義することが不可能であることがわかった。このことにより、可測集合と呼ばれる種類の部分集合にのみ長さを定義する必要が生まれた。
当然であるが、リーマン積分においても長さというものを暗黙に使用している。そうではあるが、実際のところは、リーマン積分では長方形 [a, b] × [c, d] の面積が (b - a)(d - c) で計算できることだけを基礎としている。リーマン積分は積分を近似するための「簡単に計算できる積分」として、このような長方形を並べたものだけを使っており、測度に関するより深い議論を必要としなかったのである。
現代では測度と積分は公理的に定義される。測度というのは、集合 X の適当な条件を満たす部分集合の族 Σ 上で定義された適当な条件を満たす関数 μ であれば何でもよく、X がユークリッド空間であったり、Σ の元が面積を計算したい図形であったりする必要はないし、μ の値が面積とかけ離れたものでもよい。そこで、ユークリッド空間の図形の面積を与える測度は特別にルベーグ測度という名前がついている。測度が満たすべき適当な条件については測度論を参照されたい。
積分
測度空間として (X, M, μ) が与えられたとする。例えば、X としてユークリッド空間、M をルベーグ可測集合全体、μ としてルベーグ測度などが考えられる。確率論においては測度空間としてμ(X)=1であるような測度空間(確率空間)を使う。
ルベーグ積分において、被積分関数になる関数は可測関数と呼ばれる関数である。X上で定義された実数または±∞に値をとる関数 f が可測関数あるいはM-可測関数であるとは、任意の実数aについて(a,+∞]=(a,+∞)∪{+∞}のfによる逆像がMに属すること:
が成り立つことである。複素数値関数は、その実部と虚部が共に可測関数のとき、可測関数あるいはM-可測関数であるという。このように関数の可測性を定めれば、可測関数の全体からなる集合は代数的な操作(和、差、積、商、実数倍または複素数倍)に関して閉じていることが分かる。可測関数の全体の集合は、実数体または複素数体の上の線型空間を成すことも分かる。また、完全加法族Mの性質から、R∪{+∞,-∞}の全ての部分集合Iの可測関数fによる逆像f-1(I)もMに属することも分かる。重要なことは、多くの関数列の極限に関して閉じていることである。例えば、可測関数の列 fk に対して
で与えられる関数もまた可測関数になる。従って、可測関数列が各点収束していれば極限関数もまた可測関数である。
可測関数 f に対して、そのX上での測度μについての積分
を以下の手順で構成する。
- 集合の定義関数の場合
- 可測集合 S に対して、S の定義関数
 の積分を
の積分を - で定める。これがルベーグ積分における「簡単に計算できる積分」である。
- 非負値可測単関数(simple function)の場合
- 可測集合の定義関数の有限個の線型結合
- で書ける関数を可測単関数という。
- 全てのkに対しak≧0であるとき非負値可測単関数と呼ぶ。
- その積分を
- で定める。
- 非負値可測関数の場合
- 非負値可測関数(+∞ も値として許す) f の積分を
- で定める。
- 実数値可測関数の場合
- 実数値可測関数(±∞ も値として許す) f の積分を定義する。まず f を
- と分解する。ここで
- である。このとき、両者とも非負可測関数である。さらに、
- も非負値可測関数である。
以上の準備を基に、実数値可測関数 f がルベーグ可積分であるとは
を充たす事である。このときfのμによる積分を
によって定める。
複素数値可測関数の積分は、その実部uと虚部vがルベーグ可積分であるならば、u,vの積分をα,βとするとき、α+iβで定義される。
可測集合E⊆Xでのfのルベーグ積分はf1EのX上での積分として定義される。
直感的な解釈
積分の定義方法の違いを直感的に理解できるように、山の(海抜より上の部分の)体積を計算する例を考えよう。この山の境界ははっきりと定まっているとする(これが積分範囲である)。
- リーマン積分による方法
- ケーキを切るときのように、山を縦方向に切り分けて細分する。このとき、各パーツの底面は長方形になるようにする。次に、各パーツで最も標高が高いところを調べ、底面の面積とその標高を掛け合わせる。各パーツごとに計算したその値を足したものを、上リーマン和と呼ぶことにする。同様のことを、最も標高が低いところに対して行い、下リーマン和と呼ぶことにする。分割を細かくしていったときに、上・下のリーマン和が同じ値に収束するときに、リーマン積分可能であるといい、その極限値が山の体積になる。
- ルベーグ積分による方法
- 山の等高線を地図にする。等高線にそって地図を裁断して、地図をいくつかのパーツに分解する。各パーツは面積を計算できる平面図形なので(測度が分かっているので)、パーツの面積とそのパーツの最も低い点の標高を掛け合わせる。各パーツのこの値を足したものを「ルベーグ和」と呼ぶことにする。この「ルベーグ和」はルベーグ積分の構成にあった、単関数の積分に相当する。等高線の間隔を半分にしていったときの「ルベーグ和」の極限値が山の体積になる。
例
有理数体 Q の定義関数 1Q(ディリクレの関数)を考える。この関数は至るところ不連続である。
- 1Q は [0,1] 上でリーマン可積分ではない: [0,1] をどのように区間に分割しても、各区間には有理数と無理数の両方が少なくともひとつは入っている。よって、上積分は常に 1 であり、下積分は常に 0 になり、リーマン可積分ではない。
- 1Q は [0,1] 上でルベーグ可積分である: 集合の定義関数の積分は定義より
ルベーグ積分における定理
ルベーグ積分においては零集合の上でのみ異なる値をとる関数を区別しない。 正確に言うと、関数 f と g がほとんど至るところ等しいとは
をみたすことであり、
とも書く。
- 非負値可測関数(+∞ を関数値として許す)f と g がほとんど至るところ等しいならば
- 可測関数(±∞ を関数値として許す) f と g がほとんど至るところ等しいならば、f が可積分であることと g が可積分であることは同値であり、可積分のときは積分の値も等しい。
ルベーグ積分は以下の性質を持っている。
線型性: 可積分関数 f、g と実数 a、b に対して、af + bg も可積分になり
単調性: 0≤f≤g ならば
単調収束定理: {fk}k∈N を非負値可測関数の増大列とする。つまり
このとき
が成立する。
注意: 左辺または右辺の一方が正の無限大に発散すれば、もう一方の辺も同様である。
ファトゥーの補題: {fk}k∈N を非負値可測関数の列とする。このとき
が成立する。
この定理においては左辺が正の無限大に発散すれば、右辺も正の無限大に発散する。
ルベーグの収束定理: {fk}k∈N を可測関数の列で f に概収束するとし、可積分関数 g によって、 任意の k に対して|fk| ≤ g a.e.と上下から押さえられているとする。このとき、極限関数f も可積分であり
が成立する。
他の定式化
可測関数についての分布関数の広義リーマン積分によってルベーグ積分を定義することもある。
(X,Σ,μ)を測度空間、E∈Σとするとき、任意のt≧0と非負値Σ-可測関数fに対して、Eの点で, そこでの値>tなる点全体の集合の測度をfの分布関数L(t)=μ({x∈E : f(x)>t})といい、その無限区間[0,+∞)での広義リーマン積分(=I とする)を、非負値Σ-可測関数fの可測集合E上でのルベーグ積分という。即ち、
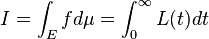 .
.
f(x)が有界(∃M≧0,∀x∈E, |f(x)|≦M)であるとき、t≧Mならば、L(t)=0である。このとき、fの本質的上限(essential supremum)ess sup(f)=inf{t∈R : L(t)=0}=mとすれば、定義式の広義リーマン積分は有界な閉区間[0,m]上でのL(t)のリーマン積分に等しくなる:
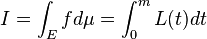 .
.
これはリーマン積分の積分区間についての加法性などから分かる。
fが有界ならばこの積分 I は必ず存在する。fが有界でない場合や、或る t に対してL(t)=+∞である場合にも、+∞も値として許せば、 I は必ず存在する。非負値Σ-可測関数の積分から、上記と全く同様に実数値Σ-可測関数と複素数値Σ-可測関数の積分も定義される。
この積分 I が有限値(I <+∞)であるとき、fはE上でルベーグ可積分またはルベーグ積分可能であるという。
この定義によるルベーグ積分に於いても、上記と同じ性質、例えば線型性や単調性、単調収束定理、ファトゥの補題、ルベーグの収束定理などが成り立つ。
測度論を全く使わない方法としては、リーマン積分はコンパクトな台を持つ任意の連続関数に対して定まっているので、関数解析の手法を用いることでより一般の関数にこの積分を拡張する方法がある。Cc を R 上定義された実数値関数でコンパクトな台を持つもの全体とする。ノルムをリーマン積分を用いて
により定める。
これにより Cc は線形ノルム空間となる。距離空間の完備化(Hausdorff completions)によって完備な空間に拡張したものを L1 とする。この空間はルベーグ可積分な関数からなる空間と(ほとんど至るところ等しい関数は同一視したとして)同型となる。さらに、リーマン積分は Cc 上の連続な線形汎関数であり、Cc は L1 の稠密な部分空間であるから、L1 上の線形汎関数にただ一通りに拡張できる。 この拡張は、ルベーグ積分と一致する。
この方法の問題点は可測関数を完備化により抽象的に得られた空間の点として定めていることであり、この抽象的な点を関数として表現する方法が自明ではないことである。とりわけ、関数列の各点収束と積分との関係を示すことは非常に難しい。This approach can be generalised to build the theory of integration with respect to Radon measures on locally compact spaces. It is the approach adopted by Bourbaki (2004); for more details see Radon measures on locally compact spaces.
参考
- "Does anyone believe that the difference between the Lebesgue and Riemann integrals can have physical significance, and that whether say, an airplane would or would not fly could depend on this difference? If such were claimed, I should not care to fly in that plane."「ルベーグ積分とリーマン積分に物理的な意味の違いがあると、たとえばそれで飛行機が飛ぶか飛ばないかが決まるなどと、誰が思う? そんなことがあったら、私は飛行機になど乗らないよ。」 リチャード・ハミング
参考文献
- 高木貞治『定本解析概論』岩波書店
- 寺澤順『はじめてのルベーグ積分』日本評論社
- 猪狩惺『実解析入門』岩波書店
- 「数学セミナー」2010年8月号、日本評論社(「実解析」とは何か)
- 新井仁之『ルベーグ積分講義』日本評論社
- 森真『ルベーグ積分超入門』共立出版
- 松浦武信・高橋宣明・吉田正廣『物理・工学のためのルベーグ積分入門』東海大学出版会
- 谷島賢二『ルベーグ積分と関数解析』朝倉書店
- R. M. Dudley, Real Analysis and Probability, Wadsworth & Brookes/Cole, 1989. Very thorough treatment, particularly for probabilists with good notes and historical references.
- P. R. Halmos, Measure Theory, D. van Nostrand Company, Inc. 1950. A classic, though somewhat dated presentation.
- L. H. Loomis, An Introduction to Abstract Harmonic Analysis, D. van Nostrand Company, Inc. 1953. Includes a presentation of the Daniell integral.
- H. Lebesgue, Oeuvres Scientifiques, L'Enseignement Mathématique, 1972
- M. E. Munroe, Introduction to Measure and Integration, Addison Wesley, 1953. Good treatment of the theory of outer measures.
- W. Rudin, Principles of Mathematical Analysis Third edition, McGraw Hill, 1976. Known asLittle Rudin, contains the basics of the Lebesgue theory, but does not treat material such asFubini's theorem.
- W. Rudin, Real and Complex Analysis, McGraw Hill, 1966. Known as Big Rudin. A complete and careful presentation of the theory. Good presentation of the Riesz extension theorems. However, there is a minor flaw (in the first edition) in the proof of one of the extension theorems, the discovery of which constitutes exercise 21 of Chapter 2.
関連項目
ディリクレの関数(ディリクレの-かんすう)とは、実数全体の成す集合 R上で定義される次のような関数のことである。
ただし、Q は有理数全体の成す集合である。 式から分かるように、この関数はいたるところで不連続である。さらに、
が成り立つから、(sup∫ を上積分、inf∫ を下積分という)ディリクレの関数はリーマン積分不可能であることが分かる。(ルベーグ積分は可能で、その値は 0 である。これは、可算無限集合である Q はルベーグ測度に関して零集合であることによる)
____
数学の実解析の分野において、リーマン積分(リーマンせきぶん、英:Riemann integral)とは、区間上の関数の積分の最初の厳密な定式化であり、ベルンハルト・リーマンによって創始された[1]。多くの関数や実際的な応用に対しては、リーマン積分は微分積分学の基本定理による計算や数値積分による近似計算が可能である。
リーマン積分は Rn の有界集合上の関数に対して定義されるが、積分範囲にある種の極限を考えることにより、広義リーマン積分が定義される。広義リーマン積分との対比で、通常のリーマン積分を狭義リーマン積分とも呼ぶ。
リーマン積分は積分の多くの性質を示すのに有効であるが、積分と極限との交換に関係する性質を示すには理論的困難を伴うなど、いくつかの技術的欠点がある。この為こうした欠点を補うべくリーマン=スティルチェス積分やルベーグ積分など積分概念の別の定式化方法も提案されている。
同じ海の体積でも
海の深さから測るのと(ルベーグ)
海の広さから測るのと(リーマン)
道具を使い分けましょう、ということ
________________
/|・・・・・・・・・・・・・・・/|
/・|・・・・・・・・・・・・・・/・|
/・・|・・・・・・・・・・・・・/・・|
/___|___________ /・・・|
|・・・・|・⇩・・・・・・・・・|・⇩・・|
|・・・・|・・・・・・・・・・・|・・・・|
|・・・・|・・・・・・⇩・・・・|・・・・|
|・・・⇩|・・・・・・・・・・・|・・・・|
|・・・・|___________|____|
|・・・/|(・・)・・・・・・・|(・)/|
|・・/・|・・・・・(・・)・・|・・/ |
|・/(・)・・・・・・・・・・・|・/ |
|/___|___________|/・ |
| | ・ | |
| | ・ ・ | ・ |
| ・| ・ | |
| | ・ | |
1| ・| ・ | |
| | | ・ |
| |_/\___/\___|____|y
| / / \ / \ |/\ /
| /・ \__// \ |--/
| / /\ \____/ | / 1
|/__--___________|/
________________
/|・・・・・・・・・・・・・・・/|
/・|・・・・・・・・・・・・・・/・|
/・・|・・・・・・・・・・・・・/・・|
/___|___________ /・・・|
|・・・・|・・・・・・・・・・・|・・・・|
|・・・・|・・・・・・・・・・・|・・・・|
|・・・・|・・・・・・・・・・・|・・・・|
|・・・・|・・・・・・・・・・・|・・・・|
|・・・・|___________|____|
|・・・/|・・・・・・・・・・・|(・)/|
|・・/・|・・・・・(・・)・・|・・/ |
|・/・・|・・・・・・・・・・・|・/ |
|/___|___________|/・ |
| | | |
| | ・ | ・ |
| | ・ | |
| | | |
| | ・ | |
| | | ・ |
| |______/\___|____|
| / / \ |/\ /
| / / \ |--/
| / \____/ | /
|/_______________|/

![f^{-1}((a,\infty]) \in M](https://upload.wikimedia.org/math/4/f/1/4f14a90c04dffbcdedab840b418b2e01.png)

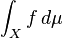

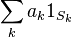


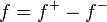

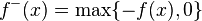

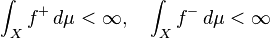
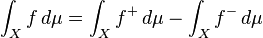
![\int_{[0,1]} 1_{\mathbf{Q}} \, d \mu = \mu(\mathbf{Q} \cap [0,1]) = 0](https://upload.wikimedia.org/math/7/6/5/765bbdb3ee46ca29e0b5b6eaf3b596ce.png)
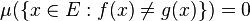


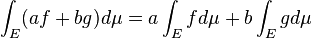












9 Comments:
wikiより
直感的な解釈
積分の定義方法の違いを直感的に理解できるように、山の(海抜より上の部分の)体積を計算する例
を考えよう。この山の境界ははっきりと定まっているとする(これが積分範囲である)。
リーマン積分による方法
ケーキを切るときのように、山を縦方向に切り分けて細分する。このとき、各パーツの底面は長方形に
なるようにする。次に、各パーツで最も標高が高いところを調べ、底面の面積とその標高を掛け合わせ
る。各パーツごとに計算したその値を足したものを、上リーマン和と呼ぶことにする。同様のことを、
最も標高が低いところに対して行い、下リーマン和と呼ぶことにする。分割を細かくしていったときに、
上・下のリーマン和が同じ値に収束するときに、リーマン積分可能であるといい、その極限値が山の
体積になる。
||
||||
||||||
||||||||
ルベーグ積分による方法
山の等高線を地図にする。等高線にそって地図を裁断して、地図をいくつかのパーツに分解する。
各パーツは面積を計算できる平面図形なので(測度が分かっているので)、パーツの面積とそのパーツ
の最も低い点の標高を掛け合わせる。各パーツのこの値を足したものを「ルベーグ和」と呼ぶことに
する。この「ルベーグ和」はルベーグ積分の構成にあった、単関数の積分に相当する。等高線の間隔
を半分にしていったときの「ルベーグ和」の極限値が山の体積になる。
__
____
______
________
■『量の測度 新装版』(最終得票数 12票)
http://www.fukkan.com/fk/CartSearchDetail?i_no=68325293&tr=s
――――――――――――――――――――――――――――――――――
【著者】アンリ・ルベーグ 著 / 柴垣和三雄 訳
【発行】みすず書房
【予価】4,104円(税込み)※予価の為、価格が変更する場合がございます。
【発送時期】2016/11/中旬
復刊リクエストコメントは
こちら
http://www.fukkan.com/fk/VoteDetail?no=37380&tr=s
『図書館で借りて読みましたが、随所に感動的な言葉が出てきます。大学の
数学科に入学したら、2年生になったぐらいには、是非読んでいただきたい本
です。数学科でなくても、解析学に興味を持つ全ての人に勧めたい本です。
また、現代の社会科学系では測度論の必要となる学問は多いですから、商、
経、社などの院に進んだ人にもお勧めです。』
『数学に興味がある。そして「数学は経験的な学問である。論理的というわ
けではない。ただ、他の学問より、あいまいな部分が少ないというだけであ
る。」などの名言も気になる。』
『歴史的な著作。復刊してください。』
(以上、リクエストコメントより)
――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――
■『量の測度 新装版』(最終得票数 12票)
http://www.fukkan.com/fk/CartSearchDetail?i_no=68325293&tr=s
――――――――――――――――――――――――――――――――――
【著者】アンリ・ルベーグ 著 / 柴垣和三雄 訳
【発行】みすず書房
【予価】4,104円(税込み)※予価の為、価格が変更する場合がございます。
【発送時期】2016/11/中旬
本書は、数学と数学教育との接点における「量」の根本原理を、著者自身の教
育経験にもとづいて明快に解説したものである。著者ルベーグは、ルベーグ積
分の創始者としてはもとより、フーリエ級数論、ポテンシャル論などの分野で
も輝かしい貢献をなしたことで著名な20世紀フランス最大の解析学者である。
長さ・面積・体積など量の概念を明確にするためには、まず量そのものと量を
表わす数とを論理的に区別しなければならない。そのうえで、量を利用して数
の概念を導入し、これをより一般の数へと拡張することが必要になる。
本書において、ルベーグは長さの測定に即して十進法にもとづく数の概念を導
入し、「相等」「和」「積」などを定義しなおす。ついで、面積、体積、およ
び曲線の長さ、曲面の面積を論じ、必然的に公理の組立てに向かわざるをえな
い理由を示す。こうした基盤のもとに量一般および微分積分法の基本をまとめ
る。
数学教育のあり方への提言として示唆に富む数学史上の古典的著作である。
▼目次
序
I 集団の比較.整数
1. 数えること
2. 算術は実験的科学である
3. 算術の応用について
4. 十進法を用いる教育学的理由
5. 続き
6. 形而上学を授業から引き離すこと
II 長さと数
7. 長さの測定によって整数から最も一般な数に移行すること
8. 数の過大近似値と過小近似値
9. 数の加法
10. 数の乗法
11. 数の減法と除法
12. 単位線分に関係しないこと
13. 数の「数学」学級での取扱いに対する教育学的批評
14. 続き.なぜ「数学」学級で無理数を避けることになるのか
15. 切断の考えを使うこと
16. 私の提案した説明法の利点
17. 続き.その意義
18. きっかりとした計算の意義について
19. 通約不能な距離の比
20. 距離の比は数である
21. 私の説明法によるタレスの定理などの証明
22. 角と弧の取扱いと数
23. 標準尺度による間接的比較
III 面積
24. 面分の面積の概念.第一の説明法.正方形網目
25. 長方形の面積
26. 多角形の面積(第一の説明法による)
27. 続き
28. 面分が面積を持つための条件
29. 合同な面分の面積
30. 長さの単位の変更
31. 面積の公理的定義
32. 多角形の面積の古典的評価式
33. 多角形の面積の第二の説明法
34. 二つの説明法の比較
35. 多角形の面積の第三の説明法(測量師の方法)
36. 教授上の問題と教師への注意
37. 面積の第四の説明法.有限同値な多角形
38. 証明には一般的な数概念に訴えることが必要
39. 続き
40. 教育学的な諸注意
41. 線分と円弧で限られた面分の面積に第一法の適用
42. ここの説明と教科書のそれとの比較
43. もっと一般な面分への適用.具体から抽象へ
IV 体積
44. 第一の説明法.立方体網目
45. 合同な立体の体積
46. 多面体の体積
47. 立体の体積の変位に対する不変性(第一の方法の変形)
48. 体積計算の簡単化
49. 続き.角錐台の体積の公式
50. 第一の説明法.面積に対する射影定理
51. 第二および第三の説明法
52. 薄片による公理α,β,γの検証
53. 教育学的諸注意.丸みを持った立体の体積
54. 面積や体積を定義する数とその数値計算について
55. ni, Niについて計算するのでなく推論することの必要性
56. 計算か推論か
57. 積分法による説明法の教育学的批判
58. 続き
59. 抽象的関数概念の困難性
60. 体積の積分法による推論の困難性
61. 整数の平方の和の計算に対する注意
V 曲線の長さと曲面の面積
62. 前置きと教育学的注意
63. 歴史的要約.幾何学的概念のコーシーによる代数化
64. 内接多角形と内接多面体の面積の極限について.シュワルツの逆説
65. 面積の古典的解析学的定義と逆説解明のためなされた諸努力
66. 長さに対する類比な逆説とそれに基づく反省
67. 曲線の長さの一般定義の提案について
68. 長さの実験的決定とその古典的解析学的定義の間の接合
69. 曲線の長さの古典的解析学的定義の汎関数概念による意味づけ
70. 曲線の長さの第一の説明法
71. 曲線の長さの存在
72. 曲線の長さの積分表示
73. 曲面積の第一の説明法とその円柱・円錐・球への適用
74. ジラールの定理の証明への応用
75. §73の面積の定義の論理的正当化
76. 続き
77. 曲面の面積の積分表示
78. 批判
79. 平面曲線の長さの第二の説明法
80. 同じく空間曲線の長さ
81. 同じく曲線の面積
82. 第二の説明法に基づく諸量の積分表示
83. 結論
VI 測定可能な量
84. 序論
85. 量とは何かを考えるにあたってのいろいろな反省
86. 物体族に定義される量の第一公理 a)
87. 続き.量の第二公理 b)
88. 関数関係にある二量についての基本的定理
89. 量の第三公理 c)
90. 諸公理についての反省
91. 比例する二量
92. ジラールの定理などへの応用
93. 幾つかの数に比例する数.古典的陳述の批判
VII 積分法と微分法
94. 序論.量(物体関数)と誘導量(点関数)
95. k次元幾何学の概要
96. 諸領域の定義
97. k次求積可能領域の定義.k次の面積とその存在条件
98. k次の面積が諸公理を満たすこと
99. 単純領域の求積可能性
100. 任意の求積可能領域の面積が公理γを満足すること
101. 面積の連続性
102. 求積可能領域Δの加法的関数f(Δ)
103. 領域関数f(Δ)の正の領域V(Δ)に関する導来数
104. 連続な点関数φ(P)のf(Δ)に関するΔの上に取られた積分
105. 平均値の定理と有限増分の定理
106. f(Δ)が積分問題の解であることの証明.記号Δφ(P)dV
107. 積分の多重積分による表現
108. 積分の累次積分による計算
109. 続き.単一積分
110. 積分法における変数変更
111. 諸領域の向き
112. 向きのある領域の上での積分の定義
113. 向きのある多様体の上の積分
114. グリーンの公式
115. 曲線の長さ・曲面の面積の諸概念の一般化
VIII 結論
本書で訂正した原著のミスプリントその他
訳者あとがき
索引
――――――――――――――――――――――――――――――――――
■キーワード『ルベーグ』商品ページ
http://www.fukkan.com/list/isearch/?tagid=4376&tr=s
ルベーグ積分30講
ルベーグ積分については以下の書がいい。
ルベーグ積分30講 1990年09月20日 志賀浩二 著
#18より
日常的な例で,関数列fnがfにー様収束しないような状況を感じとってもらおう。
図は,xy-平面上に底面がおかれた,1辺が1の立方体で,上面には大きさの違う
細かい穴が隙間のないほどいっぱいあいている.この上から細かい砂をー様に落とし
ていくとする,あるいは立方体の上面に箱を乗せ,そこに砂を詰めたと思ってもよ
い.砂は穴から下の立方体ヘと落ちていくが,穴の大きいところでは,砂はどんどん
高くなり,穴の小さいところでは,砂はごく微少な量だけ積もってくる.砂はあまり
崩れないとすると,この状況は図31で察せられるだろう.数学的に考えるときに
は,穴の大きさは(そしてまた砂粒の大きさも)いくらでも小さくとってもよいとす
る.このとき,立方体の底面(x , y)から測ったn秒後における,砂の高さをfn(x,y)
とすると,n→∞のとき,fn(x,y)→1である.これは,どの点(x,y)をとっても,
点(x,y)上で砂はいつかは立方体の上面にまで達するということである,しかし,
たとえば点(a,b)で上面の穴が小さければ,砂はごくわずかずつしか落ちないから
1万秒たっても,まだそこでの砂の高さは,1/1000に達していないかもしれない,
そのことは
f10000(a, b) < 1000
を示す,すなわち,非常に速く砂の高さが1に達する場所と,恐ろしいほど長時間た
ってから高さが1に達する場所とが散在している.このようなとき,fn(x , y)は1に
一様に収束していない.
n秒後の砂の体積を測ってみても,これが究極的には立方体を埋めつくし,体積1
となることは予想できないだろう.
________________
/|・・・・・・・・・・・・・・・/|
/・|・・・・・・・・・・・・・・/・|
/・・|・・・・・・・・・・・・・/・・|
/___|___________ /・・・|
|・・・・|・⇩・・・・・・・・・|・⇩・・|
|・・・・|・・・・・・・・・・・|・・・・|
|・・・・|・・・・・・⇩・・・・|・・・・|
|・・・⇩|・・・・・・・・・・・|・・・・|
|・・・・|___________|____|
|・・・/|(・・)・・・・・・・|(・)/|
|・・/・|・・・・・(・・)・・|・・/ |
|・/(・)・・・・・・・・・・・|・/ |
|/___|___________|/・ |
| | ・ | |
| | ・ ・ | ・ |
| ・| ・ | |
| | ・ | |
1| ・| ・ | |
| | | ・ |
| |_/\___/\___|____|y
| / / \ / \ |/\ /
| /・ \__// \ |--/
| / /\ \____/ | / 1
|/__--___________|/
x 1
あるいは以下の説明がいい、
wikiより
直感的な解釈
積分の定義方法の違いを直感的に理解できるように、山の(海抜より上の部分の)体積を計算する例
を考えよう。この山の境界ははっきりと定まっているとする(これが積分範囲である)。
リーマン積分による方法:
||
||||
||||||
||||||||
ケーキを切るときのように、山を縦方向に切り分けて細分する。このとき、各パーツの底面は長方形に
なるようにする。次に、各パーツで最も標高が高いところを調べ、底面の面積とその標高を掛け合わせ
る。各パーツごとに計算したその値を足したものを、上リーマン和と呼ぶことにする。同様のことを、
最も標高が低いところに対して行い、下リーマン和と呼ぶことにする。分割を細かくしていったときに、
上・下のリーマン和が同じ値に収束するときに、リーマン積分可能であるといい、その極限値が山の
体積になる。
ルベーグ積分による方法:
__
____
______
________
山の等高線を地図にする。等高線にそって地図を裁断して、地図をいくつかのパーツに分解する。
各パーツは面積を計算できる平面図形なので(測度が分かっているので)、パーツの面積とそのパーツ
の最も低い点の標高を掛け合わせる。各パーツのこの値を足したものを「ルベーグ和」と呼ぶことに
する。この「ルベーグ和」はルベーグ積分の構成にあった、単関数の積分に相当する。等高線の間隔
を半分にしていったときの「ルベーグ和」の極限値が山の体積になる。
伊藤清三「ルベーグ積分入門」は名著なのかも知れないが初心者にはピンと来ない
ルベーグ積分については以下の書がいい。
ルベーグ積分30講 1990年 志賀浩二 #18より
日常的な例で,関数列fnがfにー様収束しないような状況を感じとってもらおう。
図は,xy-平面上に底面がおかれた,1辺が1の立方体で,上面には大きさの違う
細かい穴が隙間のないほどいっぱいあいている.この上から細かい砂をー様に落とし
ていくとする,あるいは立方体の上面に箱を乗せ,そこに砂を詰めたと思ってもよ
い.砂は穴から下の立方体ヘと落ちていくが,穴の大きいところでは,砂はどんどん
高くなり,穴の小さいところでは,砂はごく微少な量だけ積もってくる.砂はあまり
崩れないとすると,この状況は図で察せられるだろう.数学的に考えるときに
は,穴の大きさは(そしてまた砂粒の大きさも)いくらでも小さくとってもよいとす
る.このとき,立方体の底面(x , y)から測ったn秒後における,砂の高さをfn(x,y)
とすると,n→∞のとき,fn(x,y)→1である.これは,どの点(x,y)をとっても,
点(x,y)上で砂はいつかは立方体の上面にまで達するということである,しかし,
たとえば点(a,b)で上面の穴が小さければ,砂はごくわずかずつしか落ちないから
1万秒たっても,まだそこでの砂の高さは,1/1000に達していないかもしれない,
そのことは
f10000(a, b) < 1000
を示す,すなわち,非常に速く砂の高さが1に達する場所と,恐ろしいほど長時間た
ってから高さが1に達する場所とが散在している.このようなとき,fn(x , y)は1に
一様に収束していない.
n秒後の砂の体積を測ってみても,これが究極的には立方体を埋めつくし,体積1
となることは予想できないだろう.
________________
/|・・・・・・・・・・・・・・・/|
/・|・・・・・・・・・・・・・・/・|
/・・|・・・・・・・・・・・・・/・・|
/___|___________ /・・・|
|・・・・|・・・・・・・・・・・|・・・・|
|・・・・|・・・・・・・・・・・|・・・・|
|・・・・|___________|____|
|・・・/|(・・)・・・・・・・|(・)/|
|・・/・|・・・・・(・・)・・|・・/ |
|・/(・)・・・・・・・・・・・|・/ |
|/___|___________|/・ |
| | ・ | |
| | ・ ・ | ・ |
1| ・| ・ | |
| | | ・ |
| |_/\___/\___|____|y
| / / \ / \ |/\ /
| /・ \__// \ |--/
| / /\ \____/ | / 1
|/__--___________|/
x 1
ルベーグ積分については以下の書がいい。
ルベーグ積分30講 1990年 志賀浩二 #18より
日常的な例で,関数列fnがfにー様収束しないような状況を感じとってもらおう。
図は,xy-平面上に底面がおかれた,1辺が1の立方体で,上面には大きさの違う
細かい穴が隙間のないほどいっぱいあいている.この上から細かい砂をー様に落とし
ていくとする,あるいは立方体の上面に箱を乗せ,そこに砂を詰めたと思ってもよ
い.砂は穴から下の立方体ヘと落ちていくが,穴の大きいところでは,砂はどんどん
高くなり,穴の小さいところでは,砂はごく微少な量だけ積もってくる.砂はあまり
崩れないとすると,この状況は図で察せられるだろう.数学的に考えるときに
は,穴の大きさは(そしてまた砂粒の大きさも)いくらでも小さくとってもよいとす
る.このとき,立方体の底面(x , y)から測ったn秒後における,砂の高さをfn(x,y)
とすると,n→∞のとき,fn(x,y)→1である.これは,どの点(x,y)をとっても,
点(x,y)上で砂はいつかは立方体の上面にまで達するということである,しかし,
たとえば点(a,b)で上面の穴が小さければ,砂はごくわずかずつしか落ちないから
1万秒たっても,まだそこでの砂の高さは,1/1000に達していないかもしれない,
そのことは
f10000(a, b) < 1000
を示す,すなわち,非常に速く砂の高さが1に達する場所と,恐ろしいほど長時間た
ってから高さが1に達する場所とが散在している.このようなとき,fn(x , y)は1に
一様に収束していない.
n秒後の砂の体積を測ってみても,これが究極的には立方体を埋めつくし,体積1
となることは予想できないだろう.
________________
/|・・・・・・・・・・・・・・・/|
/・|・・・・・・・・・・・・・・/・|
/・・|・・・・・・・・・・・・・/・・|
/___|___________ /・・・|
|・・・・|・・・・・・・・・・・|・・・・|
|・・・・|・・・・・・・・・・・|・・・・|
|・・・・|___________|____|
|・・・/|(・・)・・・・・・・|(・)/|
|・・/・|・・・・・(・・)・・|・・/ |
|・/(・)・・・・・・・・・・・|・/ |
|/___|___________|/・ |
| | ・ | |
| | ・ ・ | ・ |
1| ・| ・ | |
| | | ・ |
| |_/\___/\___|____|y
| / / \ / \ |/\ /
| /・ \__// \ |--/
| / /\ \____/ | / 1
|/__--___________|/
x 1
あるいは以下の説明がいい、
wikiより
直感的な解釈
積分の定義方法の違いを直感的に理解できるように、山の(海抜より上の部分の)体積を計算する例
を考えよう。この山の境界ははっきりと定まっているとする(これが積分範囲である)。
リーマン積分による方法:
||
||||
||||||
||||||||
ケーキを切るときのように、山を縦方向に切り分けて細分する。このとき、各パーツの底面は長方形に
なるようにする。次に、各パーツで最も標高が高いところを調べ、底面の面積とその標高を掛け合わせ
る。各パーツごとに計算したその値を足したものを、上リーマン和と呼ぶことにする。同様のことを、
最も標高が低いところに対して行い、下リーマン和と呼ぶことにする。分割を細かくしていったときに、
上・下のリーマン和が同じ値に収束するときに、リーマン積分可能であるといい、その極限値が山の
体積になる。
ルベーグ積分による方法:
__
____
______
________
山の等高線を地図にする。等高線にそって地図を裁断して、地図をいくつかのパーツに分解する。
各パーツは面積を計算できる平面図形なので(測度が分かっているので)、パーツの面積とそのパーツ
の最も低い点の標高を掛け合わせる。各パーツのこの値を足したものを「ルベーグ和」と呼ぶことに
する。この「ルベーグ和」はルベーグ積分の構成にあった、単関数の積分に相当する。等高線の間隔
を半分にしていったときの「ルベーグ和」の極限値が山の体積になる。
伊藤清三「ルベーグ積分入門」は名著なのかも知れないが初心者にはピンと来ない
伊藤清三「ルベーグ積分入門」は名著なのかも知れないが初心者にはピンと来ない
以下の説明がいい、
wikiより
直感的な解釈
積分の定義方法の違いを直感的に理解できるように、山の(海抜より上の部分の)体積を計算する例
を考えよう。この山の境界ははっきりと定まっているとする(これが積分範囲である)。
リーマン積分による方法:
||
||||
||||||
||||||||
ケーキを切るときのように、山を縦方向に切り分けて細分する。このとき、各パーツの底面は長方形に
なるようにする。次に、各パーツで最も標高が高いところを調べ、底面の面積とその標高を掛け合わせ
る。各パーツごとに計算したその値を足したものを、上リーマン和と呼ぶことにする。同様のことを、
最も標高が低いところに対して行い、下リーマン和と呼ぶことにする。分割を細かくしていったときに、
上・下のリーマン和が同じ値に収束するときに、リーマン積分可能であるといい、その極限値が山の
体積になる。
ルベーグ積分による方法:
__
____
______
________
山の等高線を地図にする。等高線にそって地図を裁断して、地図をいくつかのパーツに分解する。
各パーツは面積を計算できる平面図形なので(測度が分かっているので)、パーツの面積とそのパーツ
の最も低い点の標高を掛け合わせる。各パーツのこの値を足したものを「ルベーグ和」と呼ぶことに
する。この「ルベーグ和」はルベーグ積分の構成にあった、単関数の積分に相当する。等高線の間隔
を半分にしていったときの「ルベーグ和」の極限値が山の体積になる。
コメントを投稿
<< Home