例題で学ぶ 初歩からの計量経済学 白砂堤津耶(統計学初歩他)
http://nam-students.blogspot.jp/2016/03/blog-post_7.html(本頁)NAMs出版プロジェクト: 最小二乗法(直線)の簡単な説明
http://nam-students.blogspot.jp/2017/10/blog-post_6.html例題で学ぶ 初歩からの計量経済学
版情報 第2版
著者名等 白砂堤津耶/著
著者等紹介 1957年広島県生まれ。81年慶應義塾大学経済学部卒。86年慶應義塾大学大学院商
学研究科博士課程修了。現在、東京女子大学教授。専攻:計量経済学。
出版者 日本評論社
出版年 2007.3
大きさ等 22cm 298p
NDC分類 331.19
件名 計量経済学
要旨
現実経済に題材をとった例題を解くことで、計量経済学の理論とテクニックを無理なく学ぶことがでぎる画期的な入門書。ロングセラー、待望の第2版。
版情報 第2版
著者名等 白砂堤津耶/著
著者等紹介 1957年広島県生まれ。81年慶應義塾大学経済学部卒。86年慶應義塾大学大学院商
学研究科博士課程修了。現在、東京女子大学教授。専攻:計量経済学。
出版者 日本評論社
出版年 2007.3
大きさ等 22cm 298p
NDC分類 331.19
件名 計量経済学
要旨
現実経済に題材をとった例題を解くことで、計量経済学の理論とテクニックを無理なく学ぶことがでぎる画期的な入門書。ロングセラー、待望の第2版。
目次
序章.計量経済学とはどんな学問か
1.統計学の基礎知識(1)
序章.計量経済学とはどんな学問か
1.統計学の基礎知識(1)
2.統計学の基礎知識(2)
3.単純回帰モデル
4.重回帰モデル
5.回帰モデルの仮説検定と予測
6.ダミー変数
7.系列相関
8.連立方程式モデル
9.産業連関分析
10.コンピュータによる計量経済分析―TSPの基礎
目次
計量経済学とはどんな学問か
統計学の基礎知識
単純回帰モデル
重回帰モデル
回帰モデルの仮説検定と予測
ダミー変数
系列相関
連立方程式モデル
産業連関分析
コンピュータによる計量経済分析―TSPの基礎
内容
計量経済学の基本的方法を、できるだけ平易明快な表現で説明。現実経済に題材をとった例題を解くことを通じて、計量経済学の理論とテクニックを無理なく学ぶことができる画期的な入門書。ロングセラー、待望の改訂。
3.単純回帰モデル
4.重回帰モデル
5.回帰モデルの仮説検定と予測
6.ダミー変数
7.系列相関
8.連立方程式モデル
9.産業連関分析
10.コンピュータによる計量経済分析―TSPの基礎
目次
計量経済学とはどんな学問か
統計学の基礎知識
単純回帰モデル
重回帰モデル
回帰モデルの仮説検定と予測
ダミー変数
系列相関
連立方程式モデル
産業連関分析
コンピュータによる計量経済分析―TSPの基礎
内容
計量経済学の基本的方法を、できるだけ平易明快な表現で説明。現実経済に題材をとった例題を解くことを通じて、計量経済学の理論とテクニックを無理なく学ぶことができる画期的な入門書。ロングセラー、待望の改訂。
________
例題で学ぶ 初歩からの統計学
版情報 第2版
著者名等 白砂堤津耶/著
著者等紹介 1957年生まれ。81年慶應義塾大学経済学部卒。86年慶應義塾大学大学院商学研究科博士課程修了。現在、東京女子大学教授。専攻、計量経済学。主著「中国農業の計量経済分析」など。
出版者 日本評論社
出版年 2015.4
大きさ等 22cm 291p
NDC分類 417
件名 数理統計学
要旨 最短の時間で「使える統計学」がみるみる身につく!1問1問、達成感を楽しみながら学べるテキスト。さらに学習効率をアップさせた、改訂第2版。
目次
度数分布表とヒストグラムのつくり方
データの中心をはかる指標
例題で学ぶ 初歩からの統計学
版情報 第2版
著者名等 白砂堤津耶/著
著者等紹介 1957年生まれ。81年慶應義塾大学経済学部卒。86年慶應義塾大学大学院商学研究科博士課程修了。現在、東京女子大学教授。専攻、計量経済学。主著「中国農業の計量経済分析」など。
出版者 日本評論社
出版年 2015.4
大きさ等 22cm 291p
NDC分類 417
件名 数理統計学
要旨 最短の時間で「使える統計学」がみるみる身につく!1問1問、達成感を楽しみながら学べるテキスト。さらに学習効率をアップさせた、改訂第2版。
目次
度数分布表とヒストグラムのつくり方
データの中心をはかる指標
データの散らばりをはかる指標
順列と組合せ
確率
確率変数と確率分
母平均の区間推定
母比率の区間推定
仮説検定の方法(母平均の検定母比率・母平均の差・母比率の差の検定)
母標準偏差の区間推定と検定―カイ2乗分布
相関分析
回帰分析
内容
統計学の重要事項を、初歩から簡潔にわかりやすく解説し、例題を通じて「使える統計学」を短期間にマスターできる、実戦的なテキスト。さらに学習効率をアップさせ、カイ2乗分布の章を加えた第2版。
ISBN等 4-535-55790-X
ISBN等 978-4-535-55790-1
順列と組合せ
確率
確率変数と確率分
母平均の区間推定
母比率の区間推定
仮説検定の方法(母平均の検定母比率・母平均の差・母比率の差の検定)
母標準偏差の区間推定と検定―カイ2乗分布
相関分析
回帰分析
内容
統計学の重要事項を、初歩から簡潔にわかりやすく解説し、例題を通じて「使える統計学」を短期間にマスターできる、実戦的なテキスト。さらに学習効率をアップさせ、カイ2乗分布の章を加えた第2版。
ISBN等 4-535-55790-X
ISBN等 978-4-535-55790-1
_____
マンガでわかる統計学 | 高橋 信, トレンドプロ | 2004
http://www.amazon.co.jp/dp/4274065707/





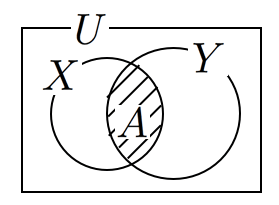
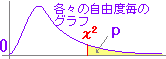 (pは右片側面積)
(pは右片側面積)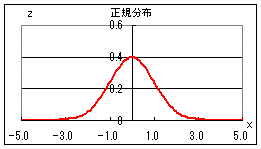
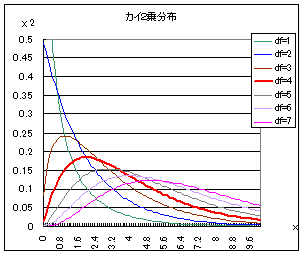
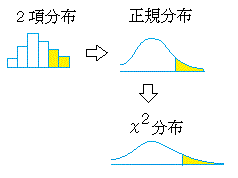
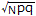 の正規分布で近似され,
の正規分布で近似され,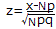
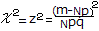 ・・・(1)
・・・(1)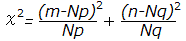 ・・・(2)
・・・(2)

 を加えたもの
を加えたもの
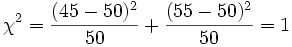

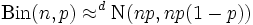
 個の変数
個の変数 から、各二乗の合計を求めると、自由度
から、各二乗の合計を求めると、自由度


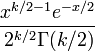
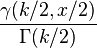


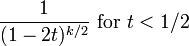




6 Comments:
例題で学ぶ初歩からの計量経済学 (単行本) の詳細
出版社: 日本評論社
レーベル:
作者: 白砂堤津耶
サイズ: 単行本
ISBN: 453555093X
発売日: 1998/03/01 関連商品リンク : 白砂堤津耶 日本評論社
【IT】日本IBM、統計解析ソフト「SPSS Statistics 25」発売--ベイズ推論の新機能 [無断転載禁止]©2ch.net
37コメント10KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1ノチラ ★2017/08/15(火) 17:31:19.41ID:CAP_USER
日本IBMは8月9日、統計解析ソフトウェア製品の最新版「IBM SPSS Statistics 25」を発売した。データの「t検定」、相関検定、線型回帰、一元配置分散分析などのベイズ統計機能を提供する。
最新版では、新しいデータ分析手法を活用するための分析機能の強化とデータ分析の生産性を高めるための機能が強化され、ユーザーの適切な意思決定を支援するという。具体的には、統計解析アルゴリズムの新機能としてベイズ推論を搭載した。
ベイズ推論はアカデミックやビジネスを問わず、近年注目されているアルゴリズム。事象が起こると考える確率(事前確率)を、その後に観測された事実によって、より客観的な確率(事後確率)を推定していく。SPSS Statistics 25では、二項検定、データの「t検定」、相関検定、線型回帰、一元配置分散分析などの機能を提供する
またユーザーのリクエストに基づき、従来の統計機能も強化。例えば、混合モデルにおける経験最良線形不偏予測量の利用や、時系列データの共変量設定も可能となり、独立および対応する現実データを分析に取り入れやすくなったという。加えて、一般線型モデルにおけるプロファイルプロット内のエラーバーの表示や、不均一分散性検定、ロバスト標準誤差などを取り入れた分析が搭載された。
さらに、データ分析の生産性を高めるため、他社アプリケーションとの連携やレポート機能も強化。図表ビルダー機能を刷新し、SPSS Statisticsで作成したグラフをMicrosoftグラフィック・オブジェクトとして利用することができるようになった。
SPSSは社会調査の統計解析ツールとして1968年にスタンフォード大学で開発され、40年以上にわたって改良が続けられている。
https://japan.zdnet.com/article/35105696/
https://www.amazon.co.jp/dp/4797366575/
図解・ベイズ統計「超」入門 あいまいなデータから未来を予測する技術 (サイエンス・アイ新書) 涌井 貞
https://images-na.ssl-images-amazon.com/images/I/618AOhMQIHL.jpg
ベイズの定理のイメージ
Bが起こったときにAの起こる確率×Bの起こる確率
=Aが起こったときにBの起こる確率×Aの起こる確率
_____ _____ _____ _____
|A尚| B| | B | |A尚|(B) | |//|
|且B| |x|_____|=|且B|//|x| |//|
|//://| |/////| | |//| |A |//|
(A)://| |//全体/| |_A|//| |__全体/|
横を縦に…
_____ __
| | | |
|_____|→| |
| |
|__|
ベン図だと3つ以上の条件が描きにくい。
上記『図解・ベイズ統計「超」入門』ではモンティ・ホール問題などもベイズ統計学で説明される。
【突き抜けた極限頭脳を持つ世界の天才スペシャル】1
https://youtu.be/D9em4Ox3ukQ?t=42m
*モンティ・ホール問題
アメリカの人気テレビ番組で行われた3つの扉から当たりを選ぶゲーム
__ __ __
| || || |
| || || |
| || || |
|__||__||__|
『実証分析のための計量経済学』山本勲、中央経済社、2015年
『計量経済学の第一歩――実証分析のススメ』田中隆一、有斐閣ストゥディア、2015年
【統計学】高校数学での統計学必修化は間違っている まったく異なる原理を持つ「数学」と「統計学」[03/05]
470コメント174KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1しじみ ★2018/03/06(火) 17:30:50.98ID:CAP_USER>>3>>18>>34>>51>>77>>84
2022年度から施行される新指導要領の案が公開され、高校の数学教育に携わる人々に激震が走っている。
最も衝撃的なのは、統計学が数学B(高校2年、理文共通)において事実上必修化され、
その割を食ってベクトルが数学C(高校3年、理系のみ)にはね飛ばされる、という変更点だ。
数学Bで必修化される統計学とは、「仮説検定」や「区間推定」などの「統計的推定」と呼ばれる方法論である。
これは小学校や中学校の統計の授業では学ばない、統計学の核心といって良い部分だ。
これまで普通は大学に入ってから学ぶものだった。
これについて、批判点は二つある。第一は、ベクトルが理系のみの学習で良いのか、という点。
第二は、統計学を数学で必修化するのは正しいか、という点。
筆者の意見では、第二の点は大問題であり、その意味で第一の点にも批判的とならざるを得ない。
■数学は「演繹的」、統計学は「帰納的」
ベクトルというのは、2次元や3次元の数を扱う代数の方法論だ。
確かに、経済学でもベクトルは必須の道具であるから、文系も学習したほうがいいという意見には同意できる。
しかし、ベクトルの計算自体は、そんなに難しいものではなく、
大学生になってから教わっても障壁が大きいわけではない。
むしろ、文系の高校生が数学という抽象的分野の中で教わるより、大学の経済学において、
経済現象という具体的なモデルをもって教わるほうがイメージよく理解できるように思える。
だから、文系にとってもっと有益な分野があるなら、ベクトルを排除しても仕方ないが、
統計学にはその価値はない。なぜなら、統計学は決して数学ではないからだ。
数学は「演繹(えんえき)的」な理論である。
これは、仮定から結論を、数理論理(「かつ」「または」「ならば」「でない」「すべて」「存在する」から展開される論理)だけで導く学問である。
だから、数学で証明された法則(定理)は常に正しい(真である)。
たとえ話で言えば、「すべてのカラスは黒い」を前提として、「だから、このカラスは黒い」を導くのが「演繹」である。
かたや、統計学は「帰納的」な理論である。
これは、観測された現象から「たぶんこうだろう」という推論を導く技術だ。
言い換えると、経験的な推論を行う理論である。
カラスのたとえで言えば、「これまで見たカラスは黒かった」を前提として、
「だからきっと、カラスというのはみんな黒いのだろう」という推論を行うのが「帰納」である。
したがって、統計学の結論では間違い(偽であること)が必然的に起きる。
このように数学と統計学は全く異なる性質の論理なのである。
続きはソースで
関連ソース画像
http://img.chess443.net/S2010/upload/2018022700003_1.jpg
WEBRONZA - 朝日新聞社の言論サイト
http://webronza.asahi.com/science/articles/2018022700003.html/
https://econ101.jp/%E3%82%A2%E3%83%AC%E3%83%83%E3%82%AF%E3%82%B9%E3%83%BB%E3%82%BF%E3%83%
90%E3%83%AD%E3%83%83%E3%82%AF%E3%80%8C%E3%83%A2%E3%83%B3%E3%83%86%E3%82%A3%E3%83%B
B%E3%83%9B%E3%83%BC%E3%83%AB%E5%95%8F%E9%A1%8C/
アレックス・タバロック「モンティ・ホール問題の直観的にわかりやすいバージョン」(2019年9月19日)
optical_frog
[Alex Tabarrok, “The Intuitive Monty Hall Problem,” Marginal Revolution, September 19, 2019]
いろんなパズルは,ある角度から眺めたときには解きにくいのに視座を変えてみたらかんたんになることがよくある.Q&Aサイトの StackExchange に,モンティ・ホール問題と本質は同じで正解を切り替えるかどうかの正しい選択が一目瞭然なものはなにか,という質問があがっている.ジョシュア・B・ミラーが,見事な回答を寄せている.おさらいしておくと,もともとのモンティ・ホール問題では,3つ並んだドアのうち1つにすてきな賞品が待っていて,回答者がどれか1つを選ぶと,司会者のモンティ・ホールが残り2つのうち1つを開けてハズレなのを見せる(開けるのは必ずハズレの方だ).これを見たあとで,ドアの選択を切り替えるか,それとも最初に選んだままにしておくか? たいていの人は,切り替えるべき理由を見出さない.あのポール・エルデシュですら,切り替えない派だった.さらに,切り替えると答える人も,たいていは,直観的にわかりにくいベイズの確率計算をやってその結論にたどり着く.
さて,その直観バージョンは次のとおり:
3人のボクサーがいる.そのうち2人は,これまでの勝敗が拮抗している(引き分けはない).あと1人のボクサーは,この2人のどちらにも必ず勝つ.
キミは当てずっぽうでボクサー A が最強だと推測して,残る2人を戦わせる.
すると,ボクサー B が C に勝利を収めた.
さて,ボクサー A と B の決戦で,キミはこのまま A 最強説をとり続けるだろうか,それとも,B の勝利に切り替えるだろうか?
Journal of Economic Perspectives にミラーが載せた論文では,モンティ・ホール問題とホットハンド・パズルを検討している.
コメントを投稿
<< Home