シュレーディンガーの猫 - Wikipedia
https://ja.wikipedia.org/wiki/シュレーディンガーの猫シュレーディンガーの猫(シュレーディンガーのねこ、英: Schrödinger's cat)またはシュレディンガーの猫は、射影公準における収縮がどの段階で起きるのかが明確でないことによって引き起こされる矛盾を示すことを狙いとした思考実験のことである[1]。
概要
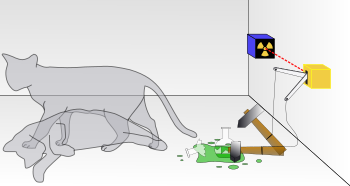
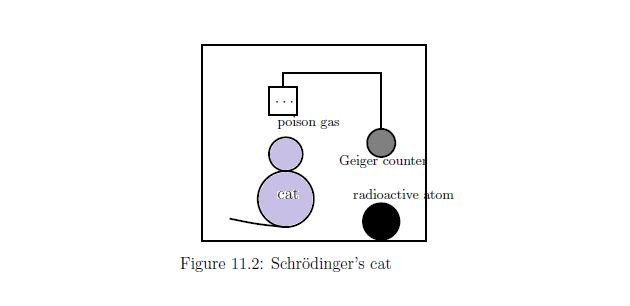
まず、蓋のある箱を用意して、この中に猫を一匹入れる。箱の中には猫の他に、放射性物質のラジウムを一定量と、ガイガーカウンターを1台、青酸ガスの発生装置を1台入れておく。もし、箱の中にあるラジウムがアルファ粒子を出すと、これをガイガーカウンターが感知して、その先についた青酸ガスの発生装置が作動し、青酸ガスを吸った猫は死ぬ。しかし、ラジウムからアルファ粒子が出なければ、青酸ガスの発生装置は作動せず、猫は生き残る。一定時間経過後、果たして猫は生きているか死んでいるか。
この系において、猫の生死はアルファ粒子が出たかどうかのみにより決定すると仮定する。そして、アルファ粒子は原子核のアルファ崩壊にともなって放出される。このとき、例えば箱に入れたラジウムが1時間以内にアルファ崩壊してアルファ粒子が放出される確率は50 %だとする。この箱の蓋を閉めてから1時間後に蓋を開けて観測したとき、猫が生きている確率は50 %、死んでいる確率も50 %である。したがって、この猫は、生きている状態と死んでいる状態が1:1で重なりあっていると解釈しなければならない。
我々は経験上、猫が生きている状態と猫が死んでいる状態という二つの状態を認識することができるが、このような重なりあった状態を認識することはない。これが科学的に大きな問題となるのは、たとえ実際に妥当な手法を用いて実験を行ったとしても、観測して得られた実験結果は既に出た結果であり、本当に知りたいことである観測の影響を受ける前の状態ではないため、実験結果そのものには意味がなく、検証のしようがないということである。
この思考実験は、(「波動関数の収縮」が、人間の「意識」によるものとした)「ノイマン-ウィグナー理論」に対する批判として、シュレーディンガーによって提出された[2]。まず、量子力学の確率解釈を容易な方法で巨視的な実験系にすることができることを示し、そこから得られる結論の異常さを示して批判したのである。シュレーディンガーは、これをパラドックスと呼んだ。
渡部鉄兵は、量子力学の標準理論の射影公準では猫の運命は認識過程によることなく測定過程としてのアルファ粒子とガイガーカウンターの相互作用が終了する時刻に決まる、測定過程に関する理論的研究は情報科学の知見も取り込んで量子測定理論と呼ばれているとしている[1]。
現在では「シュレーディンガーの猫」のような巨視的に量子力学の効果が現れる実験系が知られており、「シュレーディンガーの猫」は量子力学が引き起こす奇妙な現象を説明する際の例示に用いられる。[要出典]
「重なりあった状態」と「確率解釈」
量子力学(コペンハーゲン解釈)において粒子は、様々な状態が「重なりあった状態」で存在しうる。この「重なりあった状態」は、観測機器によって粒子を観測することで、いずれかの状態に収束すると考える。例えば、原子のスピンは、上向きの状態と下向きの状態が重なりあった状態で存在しうる。ところが、人間が観測機器によって粒子を観測すると、スピンは上向きか下向きのいずれかの状態に収束する。また、シュレーディンガー方程式は、原子の位置を一定の範囲に広がった確率分布(波動関数)として与えるが、観測されると、ある位置にあることが確定する。この実験で猫の生死を決定するアルファ粒子も同様である。
アルファ粒子は、原子核のアルファ崩壊にともなって放出される。そして、ラジウムに起こるアルファ崩壊は、量子力学によって確率解釈されなければならない。原子核は、陽子と中性子によって構成されている。正電荷をもった陽子同士は斥力によって反発するはずなのに、正電荷をもった陽子と電荷のない中性子が原子核スケールの範囲にとどまっていられるのは、核力によって引き合っているからである。原子量の小さい鉄などの原子核は、核力が支配的であるために安定しているが、原子量の大きなラジウムのような原子は、原子核のサイズが大きくなることによって核力よりも静電気力の効果が現れてくる。さて、量子力学では原子核スケールの範囲にある陽子や中性子の位置に不確定性が現れ、それらの位置は確率的にのみ決定することになる。このため、陽子や中性子は原子核の中で一定位置にあるとは考えない。しかし、陽子や中性子の位置関係によっては陽子間の斥力が核力を上回ってしまい原子核が崩壊する。このように量子力学的な揺らぎによって引き起こされる現象がアルファ崩壊であり、ラジウムのような放射性核種の原子核崩壊は量子力学的に確率解釈すべき現象である。
この実験において、ある時間内にラジウムがアルファ粒子を出すかどうかは基礎方程式(シュレーディンガー方程式の解)によって確率のみが計算でき、量子力学における確率解釈によれば、現象を観測するまでは原子核がひとつ以上崩壊した状態と原子核が全く崩壊していない状態の重ね合わせ状態で存在する。
「シュレーディンガーの猫」は粒子のようなミクロの系の重ね合わせが、猫のようなマクロの系の重ね合わせを導きうることを指摘した。[要出典] なお、現在ではシュレーディンガーの猫のように(猫ではないが)、巨視的に量子力学的現象が観測されたと報告されることがある[3][出典無効] 。
背景
量子論は、多くの科学者から、その実用的な側面で受け入れられたが、一方で量子の単一過程(たとえば、一つの原子がいつ光を輻射するか)については確率的にしかわからない、という側面を持つ。それを "不完全さ" だと主張する向きがあり、代表的な例としてはアインシュタイン=ポドルスキー=ローゼンのパラドックス(EPRパラドックス)が挙げられる。以下M.ヤンマーの解釈に従って解説する。
M.ヤンマーはこのEPRパラドックスがシュレーディンガーが猫のパラドックスを発表する背景にあった事をその著書[4]の中に記している。シュレーディンガーはその論文[5]の初めの部分にこのEPRパラドックスの結果を再確認し、それを量子力学の深刻な欠陥の一つの表れと見なした。 さらに、シュレーディンガーはこの論文でEPRパラドックスとは違った、量子力学の"欠陥"についての指摘を行った。それがシュレーディンガーの猫のパラドックスである。
シュレーディンガーの猫が指摘したもの
イリヤ・プリゴジンは、量子論としての結論は「観測結果に観測者の積極的な役割を取り入れるべきだ」というものだとしている[6]。つまり、量子的な系と観測装置まで含めた全系の状態は観測されないかぎりもつれ合ったままの関数によって記述される。 一方、量子測定理論では、理想測定と見なせる境目(Heisenberg cut)までは観測装置も量子論に従う系の一部として扱い、そこから先は射影公準により遮断できるとされる[7][8][1]。 仮に、Heisenberg cut以降を遮断できないと仮定した場合、観測装置自体を箱で囲い、観測されないようにしてしまえばどうなるであろうか。
今、量子的な系で知られるある放射性原子を考えると、原子の状態を表す関数は
|原子の状態|=|放射線を放出する|+|放射線を放出しない|
という二つの状態の重ね合わせによって表される。この放射性原子を上に示したような装置と猫とともに箱の中にしまった場合、上の主張が正しいならば、
|箱の中の状態|=|放射線が放出され猫が死んでいる|+|放射線が放出されず猫は生きている|
という重ね合わせの状態になっているはずである。つまり、箱の中では、箱を開けてそれを確認するまで、猫が死んでいるのと生きているのとが重ね合った状態になっているというのである。もし、これが現実であるとするならば、「巨視的な観測をすれば別々の状態とはっきり認める事が出来るはずの巨視的な系の諸状態は観測されていようといまいと区別される」という“状態見分けの原理”と矛盾し[9]、現実と照らし合わせて受け入れがたい。これを、M.ヤンマーは量子力学的記述が完成されていないと表現した。
このような重ね合わせの不思議さは、シュレーディンガー以前から考えられていたことであるが、M.ヤンマーはこの例が他の例と違うところは、観測という過程によって行き着く先が猫の生と死という相互に排他的でかつ相矛盾する性質を持った二つの間の選択になっているということである、と指摘している。
実用的な解決
量子測定理論によりHeisenberg cut以降は遮断できるとされており[7][8]、渡部鉄兵は、猫の運命はアルファ粒子とガイガーカウンターの相互作用が終了する時刻に決まるとしている[1]。 尚、渡部鉄兵は、観測問題の解決手段として次の条件(B)を否定した場合の批判がこの思考実験だとしている[1]。
- (A)固有値と固有状態のリンク
- (B)孤立系のシュレーディンガー方程式に従った波動関数の時間的発展
- (C)測定により測定値が得られる事実
M.ヤンマーはヒラリー・パトナムの言葉を引用している。要約すると、「たいていの物理学者はマクロスコピックな観測はつねにはっきりした値を保持していることを受け入れている。猫の例でいえば、マクロな観測とは猫が電気的に殺されるとするならばそれ自体がマクロな観測であり、猫がその電気を感じるか感じないかというそのときなのである。」
しかし、一方でパトナムはこのようにも述べている: 「しかし、シュレーディンガーの猫の持つ知的な意義は、そうしたことによって損なわれるわけではない。マクロスコピックな観測がいついかなる時もはっきりとした値を保持するという原理は量子力学という基礎から導きだされるのではなく、むしろそれは付加的な仮定として引き入れられている、ということである。」
観測問題
パトナムが指摘したように、マクロスコピックな観測がいつもはっきりした値であるという原理は、経験的に得られた仮定でしかない。つまり、実用的な問題は無いにしてもシュレーディンガーが示した量子力学の不完全性が克服されたわけではない。このことは、EPRパラドックスなどと併せて観測問題と呼ばれる。この観測問題は物質の認識や実在性と関わり科学・哲学の分野において未だ議論の続いている問題として残っている。
また、シュレーディンガーの猫を変形したものに、ウィグナーの友人のパラドックス[10]がある。これは、ガスの発生装置をランプに、猫をウィグナーの友人に置き換えたものである。この場合、箱の外の観測者が箱の中の友人に観測結果を尋ねることが観測であるのか、それとも箱の中の友人がすでに観測を終えているのかという問題が生じる。
哲学への影響
この思考実験は哲学の次の二つの分野でもしばしば議題に上る。ひとつは量子力学の解釈問題の議論の前提となる科学的定義に関する科学哲学においてである[11]。この場合は、量子力学の理論的枠組みが、従来の科学哲学に基づいた定義にそぐわないことを指摘する上で、この思考実験が引用される。そしてもうひとつは心の哲学において心の因果作用(→物理領域の因果的閉鎖性の項を参照)を議論するにあたって、量子力学の確率過程が問題となってくる場合においてである[12]。
参考文献
- ^ a b c d e 白井仁人, 東克明,森田邦久,渡部鉄兵『量子という謎 量子力学の哲学入門』勁草書房2012年ISBN978-4-326-70075-2 p3-16
- ^ 並木美喜雄(1992)「量子力学入門」岩波新書 120頁
- ^ Creation of a six-atom 'Schrödinger cat' state, Nature 438, 639-642 (1 December 2005) | doi:10.1038/nature04251, http://www.nature.com/nature/journal/v438/n7068/abs/nature04251.html
- ^ マックス・ヤンマー著/井上健訳「量子力学の哲学」p.p.245〜260
- ^ E. Schrödinger, "Die gegenwärtige Situation in der Quantenmechanik" Naturwissenschaften, 23(1935) pp.807-812 [1], pp. 823-828 [2], pp. 844-849 [3], 英訳 Proceedings of American Philosophical Society 124 (1980) pp. 323-338 [4] [5]
- ^ I.プリゴジン著/小出昭一郎・安孫子誠訳「存在から発展へ」p.p.76〜78
- ^ a b Modern Theory of Quantum Measurement and its Applications清水明/東京大学大学院
- ^ a b 「量子測定の原理とその問題点」清水明/数理科学NO.469,JULY 2002
- ^ マックス・ヤンマー著/井上健訳『量子力学の哲学』p.251
- ^ 並木美喜雄(1992)「量子力学入門」岩波新書 167頁
- ^ 高林武彦 著、保江邦夫 編 『量子力学 観測と解釈問題』 海鳴社 2001年 ISBN 4-87525-204-8
- ^ 『デイヴィッド・チャーマーズ著, 林 一訳 「意識する心」2001 ISBN 4-8269-0106-2』の407-435頁。「量子力学の解釈」
関連項目
- 量子力学
- 観測問題
- コペンハーゲン解釈
- エヴェレット解釈
- 重ね合わせ
- 量子デコヒーレンス
- pop'n music - コナミが発売した音楽シミュレーション。舟木智介(Cait Sith名義)の「シュレーディンガーの猫」という楽曲が使われている。
シュレーディンガーの猫、ウィグナーの友人とラプラスの悪魔
http://www.math.keio.ac.jp/~ishikawa/QLEJ/indexj088.html「シュレーディンガーの猫」のパラドックスを, シュレーディンガー描像の下に説明する.
「シュレーディンガーの猫」 は 量子力学で最も有名なパラドックスである. これを問題形式で説明する.
問題11.11 [シュレーディンガーの猫]
| 箱の中に猫を入れておく. 放射性元素,ガイガーカウンター,毒ガスの入っている小さい箱も入れておく. 1時間後に放射性元素からは放射能が出る可能性は 半々 とする. もし放射能が出ると,ガイガーカウンターが 鳴って,それが引き金になって 毒ガスの入っている小さい箱の扉が開く. そうすれば,毒ガスが充満して,必然的に猫が死ぬという 仕掛けである. また,放射能が出なければ,猫は 元気に生きているというわけである. もちろん,箱の窓は閉じているので,あなたは猫がどうなっているのか を知らない。 |
| 一時間後に、あなたが箱の中を見たとして,猫はどうなっているのだろうか? 生きているのか? 死んでいるのか? もちろん, 「半々」 に違いないが,この 「半々」 の意味を明確にせよ. |
[ウィグナーの友人]: 上の(b)の代わりに
|
11.5.2: 通常の解答
解答 11.12 [通常の解答 (i.e.,量子言語を使わない解答)].
として,
量子力学を 信じるとしたならば,上のシュレーディンガー方程式(11.16)を解けばよい. すなわち,
| 一時間後(秒後)のが計算できたとしよう. したがって,一時間後の箱の中の状態は, は となる (ここに, ). |
さて,内の次は観測量を次のように定める.
| つまり, として, は閉部分空間への射影作用素,また,, すなわち, 閉部分空間への射影作用素 と定める. |
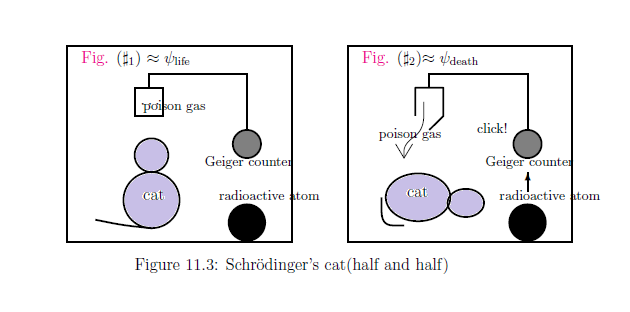
| 測定を考える. 測定値 「生」,「死」を得る確率は, 「半々」 なのだから, となるはずである. |
一時間後に,猫は「(11.18)式の意味で半死半生」の状態である。 誤解を恐れずに書くならば,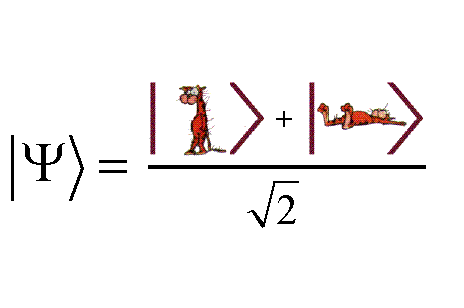 のような状態である. |
| 一時間後に,箱の窓を開けて中を見た瞬間(すなわち,測定した瞬間)に, 「元気に生きている」か 「死んでいる」かのどちらかが決定する.すなわち, |
解答 11.13 [量子言語による解答]
量子言語では量子デコヒーレンスを認めるので,,
| 時間発展して,一時間後には は, のような混合状態になったとしてもよい. |
| 測定を考える. 測定値 「生」,「死」を得る確率は, となる. |
もっと正確には, 非決定的因果作用素 を
| 測定を考える. 測定値 「生」,「死」を得る確率は, となる. |
また,
「測定した瞬間」とか「波動関数の収縮」とかは,量子言語では禁忌であるが,()は言える.
11.5.4: 要約 (Laplace's demon)
さて,
- 解答11.12(通常解答) v.s. 解答11.13(量子言語による解答)
| 通常の解答(A5)を主張して,頑張れば頑張り切る |
いかなる理論にも,「適用範囲」ある. たとえば,
|
次の二つの理論:
|
| [ラプラスの魔]: 宇宙全体のすべての物体の運動でも 国の経済成長でも, 所詮は,(無限に近い)多数の粒子系の運動方程式で 厳密に記述できて,しかも, それを解析することができる知性が存在するならば, この知性にとっては, 不確実なことは何もなくなり,その目には未来も過去も 全て見えていると考えて, このような「知性」のことを ラプラスの魔と呼ぶ. ラプラスの魔は, 「度が過ぎた実在的科学観 (すなわち,極端な物理至上主義)」 の象徴として, しばしば議論される.すなわち、 で、これと式(11.19)は比較されるべきであるが、科学の常識は、式(11.19)を選んだ。 |






0 Comments:
コメントを投稿
<< Home