Recursive Macroeconomic Theory, Thomas J. Sargent.トーマス・サージェント教授ら『再帰的マクロ経済理論』
http://nam-students.blogspot.jp/2015/07/blog-post_25.html @ (統合政府使用例)
The Big Problem of Small Change Thomas J. Sargent, François R. Velde 2002
小額貨幣にかかわる重要な問題
『物価水準の財政理論』 (FTPL, Fiscal Theory of Price Level)http://www.asyura2.com/16/hasan117/msg/112.html
http://nam-students.blogspot.com/2018/09/ftpl.html
ある不愉快なマネタリスト算術
Sargent, Thomas J. and Neil Wallace (1981), “Some Unpleasant Monetarist Arithmetic,” Federal Reserve Bank of Minneapolis Quarterly Review, Vol. 9, Fall, pp. 1-17.
(1981年のこの論考が統合政府概念のターニングポイントか)
中央銀行と政府の統合バランスシートという考えが明示されたは20c後半かもしれない
1981年のサージェント論考(後述)がターニングポイントか
1988年の邦訳では統合政府という訳語を使っていない
制約が主眼なので邦訳が間違いというわけではない
統合政府(consolidated government )再考
https://nam-students.blogspot.com/2019/12/blog-post_98.html
概念ではなく用語としての統合政府
用語としてはクラーク1937?,バルナ1945年にすでにある中央銀行と政府の統合バランスシートという考えが明示されたは20c後半かもしれない
1981年のサージェント論考(後述)がターニングポイントか
1988年の邦訳では統合政府という訳語を使っていない
制約が主眼なので邦訳が間違いというわけではない
合理的期待とインフレーション 単行本 – 1988/11
M・ウッドフォード
http://nam-students.blogspot.com/2018/09/doing-without-money-controlling-ination.html
クリストファー・シムズ - 2011年 ノ ーベル経済学賞受賞
http://nam-students.blogspot.jp/2016/11/wikipedia.html
アセモグル
http://nam-students.blogspot.com/2017/12/blog-post_22.html
サージェントが語る『経済学の12の教訓』Tom Sargent Summarizes Economics
http://nam-students.blogspot.jp/2018/03/12.html
沙金特(Dr. Thomas J. Sargent)專題講座
https://youtu.be/VWdbyd2GOw4
Prize Lecture by Thomas J. Sargent(33 minutes)
https://old.nobelprize.org/mediaplayer/index.php?id=1741
Nobel Prize Lectures of Thomas Sargent and Christopher Sims
https://youtu.be/Cl0QYkez-BE
Published on Dec 8, 2011
Nobel Prize Lectures given in Stockholm.
United States Then, Europe Now
Thomas J. Sargent, New York University, New York, NY, USA
http://bfi.uchicago.edu/files/Sargent_Sweden_11.pdf
Statistical Modeling of Monetary Policy and its Effects
Christopher A. Sims, Princeton University, Princeton, NJ, USA
http://sims.princeton.edu/yftp/Nobel/NobelLect.pdf
United States Then, Europe Now
Thomas J. Sargent, New York University, New York, NY, USA
http://bfi.uchicago.edu/files/Sargent_Sweden_11.pdf
Statistical Modeling of Monetary Policy and its Effects
Christopher A. Sims, Princeton University, Princeton, NJ, USA
http://sims.princeton.edu/yftp/Nobel/NobelLect.pdf
[マネタリストにとっては少々不愉快な算術,ある不愉快なマネタリスト算術]邦訳あり,後述
https://www.minneapolisfed.org/research/qr/qr531.pdf 全19頁
"The Stability of Models of Money and Growth with Perfect Foresight", with N. Wallace 1973, Econometrica
https://www.jstor.org/stable/1914034?seq=1#page_scan_tab_contents 有料
Thomas J. Sargent and Neil Wallace
Econometrica
Vol. 41, No. 6 (Nov., 1973), pp. 1043-1048
https://ja.wikipedia.org/wiki/%E3%83%88%E3%83%BC%E3%83%9E%E3%82%B9%E3%
83%BB%E3%82%B5%E3%83%BC%E3%82%B8%E3%82%A7%E3%83%B3%E3%83%88
トーマス・ジョン・サージェント(Thomas John Sargent、1943年7月19日 - )は、カリフォルニア州パサデナ生まれのアメリカ合衆国の経済学者。ニューヨーク大学バークレー経済学・経営学教授。専門はマクロ経済学、貨幣経済学、計量経済学における時系列分析。
1970年代から1980年代にかけて合理的期待仮説の考え方を導入し、マクロ経済学の革新を主導してきた経済学者の一人として知られる。1987年からはカリフォルニア州スタンフォードにあるフーヴァー研究所の上級フェローを務めている。
https://cruel.org/econthought/profiles/sargent.html
…
「再帰的(Recursive)」…
- いわゆる新しい古典派(ニュー・クラシカル)の第1世代に属する経済学者と一般的には見なされており、ロバート・ルーカス、ニール・ウォーレス、ロバート・バローらと共に合理的期待の考え方を取り入れ新しいマクロ経済学の手法の基礎を築いた。サージェントは典型的な合理的期待均衡を共産主義のモデル[1]と評し、鞍点経路が最適経路であり、またその鞍点経路は安定であって他の経路は排除されるという命題を発展させた。
- またマクロ経済政策についていかなる裁量的な財政・金融政策も効果が無いとする政策無効命題を提示し、従来のマクロ経済学の学説に対して真っ向から挑戦した。この挑戦はマクロ経済学及びマクロ経済政策に関して激しい論争を巻き起こし、その論争の結果サージェントらの提唱した新しいマクロ経済学の手法が受容され定着することとなった。
- また彼は貨幣的な要因に基づく景気循環理論を構築し、後の研究に大きな影響を与えた。
https://cruel.org/econthought/profiles/sargent.html
…
- "Expectations at the Short End of the Yield Curve", 1971, in Guttentag, editor, Essays on Interest Rates
- "Rational Expectations, the Real Rate of Interest and the Natural Rate of Unemployment", 1973, BPEA.
- "The Stability of Models of Money and Growth with Perfect Foresight", with N. Wallace 1973, Econometrica
- "Rational Expectations and the Dynamics of Hyperinflation", with N. Wallace, 1973, IER
- ""Rational" Expectations, the Optimal Monetary Instrument and the Optimal Money Supply Rule", with N. Wallace, 1975, JPE.
- "Rational Expectations and the Theory of Economic Policy", with N. Wallace, 1976, JME.
- "Some Unpleasant Monetarist Arithmetic", with N. Wallace, 1981, FRB Minneapolis QR
「再帰的(Recursive)」…
静的と揶揄されるケインズ、その美人コンテスト理論こそ彼らの起源である(ルーカスの島モデルの直接の手本はサミュエルソンにあるが)。ただし、マネタリズムにとどまる限り、それは無責任の体系と呼ぶべきものだ。量子力学やゲーデルと違うのは、限界を見極めるという意思の不在である。
徹頭徹尾彼らは責任を取らない。(1970年代にはルーカスとともに合理的期待形成学派をつくったが)1981年サージェントはそうした状況に以下の論文で楔を入れた…
シムズそうだがニュートラルな計量経済学的な計測によって彼らはマネタリズムから脱した。
さらに大学院生向きの教科書LSの方は、#24. Fiscal-Monetary Theories of Inflationが画期的。
必要な人は英語で読んでいるだろうが、邦訳が待たれる。
Sargent & Wallace “Some Unpleasant Monetarist Arithmetic” (1981)
[マネタリストにとっては少々不愉快な算術、ある不愉快なマネタリスト算術]
*
合理的期待とインフレーション 単行本 – 1988/11
- Rational Expectations and Inflation, 1986.
2011年ノーベル経済学賞受賞者のトーマス・J・サージェントの論文集です。
収録論文
1.「合理的期待とマクロ経済学の再構築」
2.「レーガノミックスとクレディビリティ」
3.「4大インフレーションの終焉」
4.「緩やかなインフレーションの抑制」
5.「ある不愉快なマネタリスト算術」ウォレスとの共著
6.「香港ドル投機についての考察」ビアーズとウォレスとの共著
収録論文
1.「合理的期待とマクロ経済学の再構築」
2.「レーガノミックスとクレディビリティ」
3.「4大インフレーションの終焉」
4.「緩やかなインフレーションの抑制」
5.「ある不愉快なマネタリスト算術」ウォレスとの共著
6.「香港ドル投機についての考察」ビアーズとウォレスとの共著
分析することで財政政策の重要性がわかる。マネタリストの間違いもわかる。
財政政策の役割:
物価水準を上下させる。
FTPLでは財政への見方が物価水準を決める
物価高 貨幣価値小
-------------------
⬆︎ 財政赤字は拡大するだろう
___________________________物価水準
⬇︎ 財政が再建されていくだろう
-------------------
-------------------
⬆︎ 財政赤字は拡大するだろう
___________________________物価水準
⬇︎ 財政が再建されていくだろう
-------------------
現在 将来
物価低 貨幣価値大
金融政策の役割:
名目金利が物価の“坂”を作る
物価高 貨幣価値小
 ̄-_ _- ̄
 ̄-_ _- ̄
金利引き下げ⬆︎  ̄-_ _- ̄
___________ _- ̄____________物価水準
金利引き上げ⬇︎ _- ̄  ̄-_
_- ̄  ̄-_
_- ̄  ̄-_
現在 将来
 ̄-_ _- ̄
 ̄-_ _- ̄
金利引き下げ⬆︎  ̄-_ _- ̄
___________ _- ̄____________物価水準
金利引き上げ⬇︎ _- ̄  ̄-_
_- ̄  ̄-_
_- ̄  ̄-_
現在 将来
物価低 貨幣価値大
穏やかな物価上昇[下降]を取り戻す手段
(名目金利が物価の“坂”を作る)
[金利引き下げすぐに物価上昇⬆︎] 物価高 貨幣価値小
 ̄-_ _- ̄穏やかな
 ̄-_  ̄-_ _- ̄ 物価上昇②
 ̄-_  ̄-_ _- ̄ 物価上昇②
 ̄-_  ̄-_ _- ̄
_______ ̄-__ _- ̄____________物価水準
②金利引き上げて⬇︎ _- ̄_ ⬆︎  ̄-_ (財政政策が全体を上[下])
物価上昇を _- ̄  ̄-_  ̄-_
先送り_- ̄ ①  ̄-_  ̄-_
財政への見方の変化 ̄-_
 ̄-_デフレの現状
現在 将来
物価低 貨幣価値大
全体の底上げで財政政策①の有効性を表している。
左右、現在将来のバランスで貨幣の中立性を前提としたフィッシャー*的な金利政策②の
効果を表している。
デフレでは財政政策①が重要。公共政策による一時的財政悪化は必ずしも悪いとは限らない。
*フィッシャー方程式:
(1+名目金利)÷(1+自然利子率)=(1+予想物価上昇率)
《物価の「水準」を上下させるのが財政への見方で、「坂」を動かすのが金融政策とすると矛盾は解消されるというのが私たちの整理だった。金融政策の役割とは、物価に加わる圧力を、現在から将来にかけて分散させることに過ぎないわけだ。》岩村充2017
「インフレは財政拡張だけでは生じない」物価水準の財政理論(FTPL)とは 岩村充 2017
https://www.weekly-economist.com/2017/01/31/インフレは財政拡張だけでは生じない-財政と物価の理論とは-岩村充-早稲田大学大学院教授インタビュー/
《[s0=W-1/P0のような]「追加的な条件式」の援けを借りないと均衡物価が決定されない…Ljungqvist and Sargent(2000)の第17章[2004年第2版では#24]はこの点についてわかりやすく解説している。》渡辺努、岩村充『新しい物価理論』2004年#2,52頁(1981年論文に関しては171頁)
#24. Fiscal-Monetary Theories of Inflation 857
Ljungquist_Recursive_macroeconomic_theory - LARS LJUNGQVIST THOMAS J.
以下の第三版2012年版は#14.Asset Pricing Empirics,#24. Credible Government Policies II, #39 .Foundations of Aggregate Labor Supplyが追加された。
__
Recursive Macroeconomic Theory (英語) ハードカバー – 2012/8/31
- Recursive Macroeconomic Theory Lars Ljungqvist
- ハードカバー
- 出版社: The MIT Press; third版 (2012/8/31)
¥ 12,042
OFF:
¥ 169 (1%)
¥ 169 (1%)

(類書)
Recursive Methods in Economic Dynamics
Nancy L. Stokey Nancy L. Stokey (著), Robert E. Lucas Jr. (著), Edward C. Prescott (著)
ちなみに、こちらは通称SLP
__________________
以下、両方second ed.になっているのでまぎらわしい。
2000
http://www.econ.yale.edu/smith/econ510a/sargent3.pdf (リンク切れ?)
Recursive Macroeconomic Theory
http://pages.stern.nyu.edu/~dbackus/Identification/LS%20RMT2ed%2004.pdf
Exercises in Recursive Macroeconomic Theory
(Adobe PDF)
Introduction. This is a first version of the solutions to the exercises in Recursive Macroeco- nomic Therory, First Edition, 2000, MIT press, by Lars Ljungqvist and Thomas J. Sargent. This solution manuscript is currently only available on the web.
LS recursive macroeconomic theory SECOND EDITION
目次
Unformatted text preview: LARS LJUNGQVIST THOMAS J. SARGENT r ecursive macroeconomic theory SECOND EDITION Recursive Macroeconomic Theory Second edition 2004(1st.2000)
第1版は下記url
http://www.econ.yale.edu/smith/econ510a/sargent3.pdf
第1版は下記url
http://www.econ.yale.edu/smith/econ510a/sargent3.pdf
Contents
Acknowledgements xvii Preface to the second edition xviii
Part I: The imperialism of recursive methods
1. Overview 3
1.1. Warning. 1.2. A common ancestor. 1.3. The savings problem. 1.3.1. Linear quadratic permanent income theory. 1.3.2. Precautionary saving. 1.3.3. Complete markets, insurance, and the distribution of wealth. 1.3.4. Bewley models. 1.3.5. History dependence in standard consumption models. 1.3.6. Growth theory. 1.3.7. Limiting results from dynamic optimal taxation. 1.3.8. Asset pricing. 1.3.9. Multiple assets. 1.4. Recursive methods. 1.4.1. Methodology: dynamic programming issues a challenge. 1.4.2. Dynamic programming challenged. 1.4.3. Imperialistic response of dynamic programming. 1.4.4. History dependence and dynamic programming squared. 1.4.5. Dynamic principal-agent problems. 1.4.6. More applications. v vi Contents
Part II: Tools
2. Time Series 29
2.1. Two workhorses. 2.2. Markov chains. 2.2.1. Stationary distributions. 2.2.2. Asymptotic stationarity. 2.2.3. Expectations. 2.2.4. Forecasting functions. 2.2.5. Invariant functions and ergodicity. 2.2.6. Simulating a Markov chain. 2.2.7. The likelihood function. 2.3. Continuousstate Markov chain. 2.4. Stochastic linear dierence equations. 2.4.1. First and second moments. 2.4.2. Impulse response function. 2.4.3. Prediction and discounting. 2.4.4. Geometric sums of quadratic forms. 2.5. Population regression. 2.5.1. The spectrum. 2.5.2. Examples. 2.6. Example: the LQ permanent income model. 2.6.1. Invariant subspace approach. 2.7. The term structure of interest rates. 2.7.1. A stochastic discount factor. 2.7.2. The log normal bond pricing model. 2.7.3. Slope of yield curve depends on serial correlation of log mt+1 . 2.7.4. Backus and Zins stochastic discount factor. 2.7.5. Reverse engineering a stochastic discount factor. 2.8. Estimation. 2.9. Concluding remarks. A. A linear dierence equation. 2.11. Exercises.
3. Dynamic Programming 85
3.1. Sequential problems. 3.1.1. Three computational methods. 3.1.2. Cobb-Douglas transition, logarithmic preferences. 3.1.3. Euler equations. 3.1.4. A sample Euler equation. 3.2. Stochastic control problems. 3.3. Concluding remarks. 3.4. Exercise.
4. Practical Dynamic Programming
4.1. The curse of dimensionality. 4.2. Discretization of state space. 4.3. Discrete-state dynamic programming. 4.4. Application of Howard improvement algorithm. 4.5. Numerical implementation. 4.5.1. Modied policy iteration. 4.6. Sample Bellman equations. 4.6.1. Example 1: calculating expected utility. 4.6.2. Example 2: risk-sensitive preferences. 4.6.3. Example 3: costs of business cycles. 4.7. Polynomial approximations. 4.7.1. Recommended computational strategy. 4.7.2. Chebyshev polynomials. 4.7.3. Algorithm: summary. 4.7.4. Shape-preserving splines. 4.8. Concluding remarks. 95 Contents
5. Linear Quadratic Dynamic Programming vii 109
5.1. Introduction. 5.2. The optimal linear regulator problem. 5.2.1. Value function iteration. 5.2.2. Discounted linear regulator problem. 5.2.3. Policy improvement algorithm. 5.3. The stochastic optimal linear regulator problem. 5.3.1. Discussion of certainty equivalence. 5.4. Shadow prices in the linear regulator. 5.4.1. Stability. 5.5. A Lagrangian formulation. 5.6. The Kalman lter. 5.6.1. Muths example. 5.6.2. Jovanovics example. 5.7. Concluding remarks. A. Matrix formulas. B. Linear quadratic approximations. 5.B.1. An example: the stochastic growth model. 5.B.2. Kydland and Prescotts method. 5.B.3. Determination of z . 5.B.4. Log linear approximation. 5.B.5. Trend removal. ¯ 5.10. Exercises.
6. Search, Matching, and Unemployment 139
6.1. Introduction. 6.2. Preliminaries. 6.2.1. Nonnegative random variables. 6.2.2. Mean-preserving spreads. 6.3. McCalls model of intertemporal job search. 6.3.1. Eects of mean preserving spreads. 6.3.2. Allowing quits . 6.3.3. Waiting times. 6.3.4. Firing . 6.4. A lake model. 6.5. A model of career choice. 6.6. A simple version of Jovanovics matching model. 6.6.1. Recursive formulation and solution. 6.6.2. Endogenous statistics. 6.7. A longer horizon version of Jovanovics model. 6.7.1. The Bellman equations. 6.8. Concluding remarks. A. More numerical dynamic programming. 6.A.1. Example 4: search. 6.A.2. Example 5: a Jovanovic model. 6.10. Exercises.
Part III: Competitive equilibria and applications
7. Recursive (Partial) Equilibrium
7.1. An equilibrium concept. 7.2. Example: adjustment costs. 7.2.1. A planning problem. 7.3. Recursive competitive equilibrium. 7.4. Markov perfect equilibrium. 7.4.1. Computation. 7.5. Linear Markov perfect equilibria. 7.5.1. An example. 7.6. Concluding remarks. 7.7. Exercises. 191 viii Contents
8. Equilibrium with Complete Markets 208
8.1. Time 0 versus sequential trading. 8.2. The physical setting: preferences and endowments. 8.3. Alternative trading arrangements. 8.3.1. History dependence. 8.4. Pareto problem. 8.4.1. Time invariance of Pareto weights. 8.5. Time 0 trading: Arrow-Debreu securities. 8.5.1. Equilibrium pricing function. 8.5.2. Optimality of equilibrium allocation. 8.5.3. Equilibrium computation. 8.5.4. Interpretation of trading arrangement. 8.6. Examples. 8.6.1. Example 1: risk sharing. 8.6.2. Example 2: no aggregate uncertainty. 8.6.3. Example 3: periodic endowment processes. 8.7. Primer on asset pricing. 8.7.1. Pricing redundant assets. 8.7.2. Riskless consol. 8.7.3. Riskless strips. 8.7.4. Tail assets. 8.7.5. Pricing one-period returns. 8.8. Sequential trading: Arrow securities. 8.8.1. Arrow securities. 8.8.2. Insight: wealth as an endogenous state variable. 8.8.3. Debt limits. 8.8.4. Sequential trading. 8.8.5. Equivalence of allocations. 8.9. Recursive competitive equilibrium. 8.9.1. Endowments governed by a Markov process. 8.9.2. Equilibrium outcomes inherit the Markov property. 8.9.3. Recursive formulation of optimization and equilibrium. 8.10. j -step pricing kernel. 8.10.1. Arbitrage-free pricing. 8.11. Consumption strips and the cost of business cycles. 8.11.1. Link to business cycle costs. 8.12. Gaussian asset-pricing model. 8.13. Recursive version of Pareto problem. 8.14. Static models of trade. 8.15. Closed economy model. 8.15.1. Two countries under autarky. 8.15.2. Welfare measures. 8.16. Two countries under free trade. 8.16.1. Small country assumption. 8.17. A tari. 8.17.1. Nash tari. 8.18. Concluding remarks. 8.19. Exercises.
9. Overlapping Generations Models
9.1. Endowments and preferences. 9.2. Time 0 trading. 9.2.1. Example equilibrium. 9.2.2. Relation to the welfare theorems. 9.2.3. Nonstationary equilibria. 9.2.4. Computing equilibria. 9.3. Sequential trading. 9.4. Money. 9.4.1. Computing more equilibria. 9.4.2. Equivalence of equilibria. 9.5. Decit nance. 9.5.1. Steady states and the Laer curve. 9.6. Equivalent setups. 9.6.1. The economy. 9.6.2. Growth. 9.7. Optimality and the existence of monetary equilibria. 9.7.1. Balasko-Shell criterion for optimality. 9.8. Within-generation heterogeneity. 9.8.1. Nonmonetary equilibrium. 9.8.2. Monetary equilibrium. 9.8.3. Nonstationary equilibria. 9.8.4. The real bills doctrine. 9.9. Gift-giving equilibrium. 9.10. Concluding remarks. 9.11. Exercises. 264 Contents
10. Ricardian Equivalence ix 312
10.1. Borrowing limits and Ricardian equivalence. 10.2. Innitely lived agent economy. 10.2.1. Solution to consumption/savings decision. 10.3. Government. 10.3.1. Eect on household. 10.4. Linked generations interpretation. 10.5. Concluding remarks.
11. Fiscal Policies in the Growth Model 323
11.1. Introduction. 11.2. Economy. 11.2.1. Preferences, technology, information. 11.2.2. Components of a competitive equilibrium. 11.2.3. Competitive equilibria with distorting taxes. 11.2.4. The household: no-arbitrage and asset-pricing formulas. 11.2.5. User cost of capital formula. 11.2.6. Firm. 11.3. Computing equilibria. 11.3.1. Inelastic labor supply. 11.3.2. The equilibrium steady state. 11.3.3. Computing the equilibrium path with the shooting algorithm. 11.3.4. Other equilibrium quantities. 11.3.5. Steady-state R and s/q . 11.3.6. Lump-sum taxes available. 11.3.7. No lump-sum taxes available. 11.4. A digression on back-solving. 11.5. Eects of taxes on equilibrium allocations and prices. 11.6. Transition experiments. 11.7. Linear approximation. 11.7.1. Relationship between the λi s. 11.7.2. Once-and-for-all jumps. 11.7.3. Simplication of formulas. 11.7.4. A one-time pulse. 11.7.5. Convergence rates and anticipation rates. 11.8. Elastic labor supply. 11.8.1. Steady-state calculations. 11.8.2. A digression on accuracy: Euler equation errors. 11.9. Growth. 11.10. Concluding remarks. A. Log linear approximations. 11.12. Exercises.
12. Recursive Competitive Equilibria
12.1. Endogenous aggregate state variable. 12.2. The stochastic growth model. 12.3. Lagrangian formulation of the planning problem. 12.4. Time 0 trading: Arrow-Debreu securities. 12.4.1. Household. 12.4.2. Firm of type I. 12.4.3. Firm of type II. 12.4.4. Equilibrium prices and quantities. 12.4.5. Implied wealth dynamics. 12.5. Sequential trading: Arrow securities. 12.5.1. Household. 12.5.2. Firm of type I. 12.5.3. Firm of type II. 12.5.4. Equilibrium prices and quantities. 12.5.5. Financing a type II rm. 12.6. Recursive formulation. 12.6.1. Technology is governed by a Markov process. 12.6.2. Aggregate state of the economy. 12.7. Recursive formulation of the planning problem. 12.8. Recursive formulation of sequential trading. 12.8.1. A Big K , little k trick. 12.8.2. Price system. 12.8.3. Household problem. 12.8.4. Firm of type I. 12.8.5. Firm of type II. 12.9. Recursive competitive equilibrium. 366 x Contents 12.9.1. Equilibrium restrictions across decision rules. 12.9.2. Using the planning problem. 12.10. Concluding remarks.
13. Asset Pricing 392
13.1. Introduction. 13.2. Asset Euler equations. 13.3. Martingale theories of consumption and stock prices. 13.4. Equivalent martingale measure. 13.5. Equilibrium asset pricing . 13.6. Stock prices without bubbles. 13.7. Computing asset prices. 13.7.1. Example 1: logarithmic preferences. 13.7.2. Example 2: a nite-state version. 13.7.3. Example 3: asset pricing with growth. 13.8. The term structure of interest rates. 13.9. State-contingent prices. 13.9.1. Insurance premium. 13.9.2. Man-made uncertainty. 13.9.3. The Modigliani-Miller theorem. 13.10. Government debt. 13.10.1. The Ricardian proposition. 13.10.2. No Ponzi schemes. 13.11. Interpretation of risk-aversion parameter. 13.12. The equity premium puzzle. 13.13. Market price of risk. 13.14. HansenJagannathan bounds. 13.14.1. Inner product representation of the pricing kernel. 13.14.2. Classes of stochastic discount factors. 13.14.3. A Hansen-Jagannathan bound. 13.14.4. The Mehra-Prescott data. 13.15. Factor models. 13.16. Heterogeneity and incomplete markets. 13.17. Concluding remarks. 13.18. Exercises.
14. Economic Growth 449
14.1. Introduction. 14.2. The economy. 14.2.1. Balanced growth path. 14.3. Exogenous growth. 14.4. Externality from spillovers. 14.5. All factors reproducible. 14.5.1. One-sector model. 14.5.2. Two-sector model. 14.6. Research and monopolistic competition. 14.6.1. Monopolistic competition outcome. 14.6.2. Planner solution. 14.7. Growth in spite of nonreproducible factors. 14.7.1. Core of capital goods produced without nonreproducible inputs. 14.7.2. Research labor enjoying an externality. 14.8. Concluding comments. 14.9. Exercises.
15. Optimal Taxation with Commitment
15.1. Introduction. 15.2. A nonstochastic economy. 15.2.1. Government. 15.2.2. Households. 15.2.3. Firms. 15.3. The Ramsey problem. 15.4. Zero capital tax. 15.5. Limits to redistribution. 15.6. Primal approach to the Ramsey problem. 15.6.1. Constructing the Ramsey plan. 15.6.2. Revisiting a zero capital tax. 15.7. Taxation of initial capital. 15.8. Nonzero capital tax due to incomplete taxation. 15.9. A stochastic economy. 15.9.1. Government. 15.9.2. Households. 15.9.3. Firms. 478 Contents xi 15.10. Indeterminacy of state-contingent debt and capital taxes. 15.11. The Ramsey plan under uncertainty. 15.12. Ex ante capital tax varies around zero. 15.12.1. Sketch of the proof of Proposition 2. 15.13. Examples of labor tax smoothing . 15.13.1. Example 1: gt = g for all t 0 . 15.13.2. Example 2: gt = 0 for t = T , and gT > 0 . 15.13.3. Example 3: gt = 0 for t = T , and gT is stochastic. 15.14. Lessons for optimal debt policy. 15.15. Taxation without state-contingent debt. 15.15.1. Future values of {gt } become deterministic. 15.15.2. Stochastic {gt } but special preferences. 15.15.3. Example 3 revisited: gt = 0 for t = T , and gT is stochastic. 15.16. Zero tax on human capital. 15.17. Should all taxes be zero?. 15.18. Concluding remarks. 15.19. Exercises.
Part IV: The savings problem and Bewley models
Part IV: The savings problem and Bewley models
16. Self-Insurance 545
16.1. Introduction. 16.2. The consumers environment. 16.3. Nonstochastic endowment. 16.3.1. An ad hoc borrowing constraint: nonnegative assets. 16.3.2. Example: periodic endowment process. 16.4. Quadratic preferences. 16.5. Stochastic endowment process: i.i.d. case. 16.6. Stochastic endowment process: general case. 16.7. Economic intuition. 16.8. Concluding remarks. A. Supermartingale convergence theorem. 16.10. Exercises.
17. Incomplete Markets Models
17.1. Introduction. 17.2. A savings problem. 17.2.1. Wealth-employment distributions. 17.2.2. Reinterpretation of the distribution λ . 17.2.3. Example 1: a pure credit model. 17.2.4. Equilibrium computation. 17.2.5. Example 2: a model with capital. 17.2.6. Computation of equilibrium. 17.3. Unication and further analysis. 17.4. Digression: the nonstochastic savings problem. 17.5. Borrowing limits: natural and ad hoc. 17.5.1. A candidate for a single state variable. 17.5.2. Supermartingale convergence again. 17.6. Average assets as a function of r. 17.7. Computed examples. 17.8. Several Bewley models. 17.8.1. Optimal stationary allocation. 17.9. A model with capital and private IOUs. 17.10. Private IOUs only. 17.10.1. Limitation of what credit can achieve. 17.10.2. Proximity of r to ρ . 17.10.3. Inside money or free banking interpretation. 17.10.4. Bewleys basic model of at money. 17.11. A model of seigniorage. 17.12. Exchange rate indeterminacy. 17.12.1. Interest on 566 xii Contents currency. 17.12.2. Explicit interest. 17.12.3. The upper bound on M . p 17.12.4. A very special case. 17.12.5. Implicit interest through deation. 17.13. Precautionary savings. 17.14. Models with uctuating aggregate variables. 17.14.1. Aiyagaris model again. 17.14.2. Krusell and Smiths extension. 17.15. Concluding remarks. 17.16. Exercises.
Part V: Recursive contracts
18. Dynamic Stackelberg Problems 615
18.1. History dependence. 18.2. The Stackelberg problem. 18.3. Solving the Stackelberg problem. 18.3.1. Step 1: solve an optimal linear regulator. 18.3.2. Step 2: use the stabilizing properties of shadow price P yt . 18.3.3. Stabilizing solution. 18.3.4. Step 3: convert implementation multipliers. 18.3.5. History-dependent representation of decision rule. 18.3.6. Digression on determinacy of equilibrium. 18.4. A large rm with a competitive fringe. 18.4.1. The competitive fringe. 18.4.2. The monopolists problem. 18.4.3. Equilibrium representation. 18.4.4. Numerical example. 18.5. Concluding remarks. A. The stabilizing µt = P yt . B. Matrix linear dierence equations. C. Forecasting formulas. 18.9. Exercises.
19. Insurance Versus Incentives
19.1. Insurance with recursive contracts. 19.2. Basic environment. 19.3. One-sided no commitment. 19.3.1. Self-enforcing contract. 19.3.2. Recursive formulation and solution. 19.3.3. Recursive computation of contract . 19.3.4. Prots. 19.3.5. P (v ) is strictly concave and continuously dierentiable. 19.3.6. Many households. 19.3.7. An example. 19.4. A Lagrangian method. 19.5. Insurance with asymmetric information. 19.5.1. Eciency implies bs1 bs , ws1 ws . 19.5.2. Local upward and downward constraints are enough. 19.5.3. Concavity of P . 19.5.4. Local downward constraints always bind. 19.5.5. Coinsurance. 19.5.6. P (v ) is a martingale. 19.5.7. Comparison to model with commitment problem. 19.5.8. Spreading continuation values. 19.5.9. Martingale convergence and poverty. 19.5.10. Extension to general equilibrium. 19.5.11. Comparison with self-insurance. 19.6. Insurance with unobservable storage. 19.6.1. Feasibility. 19.6.2. Incentive compatibility. 19.6.3. Ecient allocation. 19.6.4. The case of two periods ( T = 2 ). 19.6.5. Role of the planner. 19.6.6. Decentralization in a 636 Contents xiii closed economy. 19.7. Concluding remarks. A. Historical development. 19.A.1. Spear and Srivastava. 19.A.2. Timing. 19.A.3. Use of lotteries. 19.9. Exercises.
20. Equilibrium without Commitment 697
20.1. Two-sided lack of commitment. 20.2. A closed system. 20.3. Recursive formulation. 20.4. Equilibrium consumption. 20.4.1. Consumption dynamics. 20.4.2. Consumption intervals cannot contain each other. 20.4.3. Endowments are contained in the consumption intervals. 20.4.4. All consumption intervals are nondegenerate (unless autarky is the only sustainable allocation). 20.5. Pareto frontier and ex ante division of the gains. 20.6. Consumption distribution. 20.6.1. Asymptotic distribution. 20.6.2. Temporary imperfect risk sharing. 20.6.3. Permanent imperfect risk sharing. 20.7. Alternative recursive formulation. 20.8. Pareto frontier revisited. 20.8.1. Values are continuous in implicit consumption. 20.8.2. Dierentiability of the Pareto frontier. 20.9. Continuation values a la Kocherlakota. 20.9.1. Asymptotic distribution ` is nondegenerate for imperfect risk sharing (except for when S = 2 ). 20.9.2. Continuation values do not always respond to binding participation constraints. 20.10. A two-state example: amnesia overwhelms memory. 20.10.1. Pareto frontier. 20.10.2. Interpretation. 20.11. A three-state example. 20.11.1. Perturbation of parameter values. 20.11.2. Pareto frontier. 20.12. Empirical motivation. 20.13. Generalization . 20.14. Decentralization. 20.15. Endogenous borrowing constraints. 20.16. Concluding remarks. 20.17. Exercises.
21. Optimal Unemployment Insurance
21.1. History-dependent unemployment insurance. 21.2. A one-spell model. 21.2.1. The autarky problem. 21.2.2. Unemployment insurance with full information. 21.2.3. The incentive problem. 21.2.4. Unemployment insurance with asymmetric information. 21.2.5. Computed example. 21.2.6. Computational details. 21.2.7. Interpretations. 21.2.8. Extension: an on-the-job tax. 21.2.9. Extension: intermittent unemployment spells. 21.3. A multiple-spell model with lifetime contracts. 21.3.1. The setup. 21.3.2. A recursive lifetime contract. 21.3.3. Compensation dynamics when unemployed. 21.3.4. Compensation dynamics while employed. 21.3.5. Summary. 21.4. Concluding remarks. 21.5. Exercises. 751 xiv Contents
22. Credible Government Policies 773
22.1. Introduction. 22.2. Dynamic programming squared: synopsis. 22.3. The one-period economy. 22.3.1. Competitive equilibrium. 22.3.2. The Ramsey problem. 22.3.3. Nash equilibrium. 22.4. Examples of economies. 22.4.1. Taxation example. 22.4.2. Black-box example with discrete-choice sets. 22.5. Reputational mechanisms: General idea. 22.5.1. Dynamic programming squared. 22.6. The innitely repeated economy. 22.6.1. A strategy prole implies a history and a value. 22.6.2. Recursive formulation. 22.7. Subgame perfect equilibrium (SPE). 22.8. Examples of SPE. 22.8.1. Innite repetition of one-period Nash equilibrium. 22.8.2. Supporting better outcomes with trigger strategies. 22.8.3. When reversion to Nash is not bad enough. 22.9. Values of all SPEs. 22.9.1. The basic idea of dynamic programming squared. 22.10. Self-enforcing SPE. 22.10.1. The quest for something worse than repetition of Nash outcome. 22.11. Recursive strategies. 22.12. Examples of SPE with recursive strategies. 22.12.1. Innite repetition of Nash outcome. 22.12.2. Innite repetition of a better-than-Nash outcome. 22.12.3. Something worse: a stick-and-carrot strategy. 22.13. The best and the worst SPE values. 22.13.1. When v1 is outside the candidate set. 22.14. Examples: alternative ways to achieve the worst. 22.14.1. Attaining the worst, method 1. 22.14.2. Attaining the worst, method 2. 22.14.3. Attaining the worst, method 3. 22.14.4. Numerical example. 22.15. Interpretations. 22.16. Concluding remarks. 22.17. Exercises.
23. Two Topics in International Trade
23.1. Two dynamic contracting problems. 23.2. Lending with moral hazard and dicult enforcement. 23.2.1. Autarky. 23.2.2. Investment with full insurance. 23.2.3. Limited commitment and unobserved investment. 23.2.4. Optimal capital outows under distress. 23.3. Gradualism in trade policy. 23.3.1. Closed-economy model. 23.3.2. A Ricardian model of two countries under free trade. 23.3.3. Trade with a tari. 23.3.4. Welfare and Nash tari. 23.3.5. Trade concessions. 23.3.6. A repeated tari game. 23.3.7. Time-invariant transfers. 23.3.8. Gradualism: time-varying trade policies. 23.3.9. Baseline policies. 23.3.10. Multiplicity of payos and continuation values. 23.4. Concluding remarks. A. Computations for Atkesons model. 23.6. Exercises. 820 Contents xv
Part VI: Classical monetary economics and search
Part VI: Classical monetary economics and search
24. Fiscal-Monetary Theories of Inflation 857
24.1. The issues. 24.2. A shopping time monetary economy. 24.2.1. Households. 24.2.2. Government. 24.2.3. Equilibrium. 24.2.4. Short run versus long run. 24.2.5. Stationary equilibrium. 24.2.6. Initial date (time 0). 24.2.7. Equilibrium determination. 24.3. Ten monetary doctrines. 24.3.1. Quantity theory of money. 24.3.2. Sustained decits cause ination. 24.3.3. Fiscal prerequisites of zero ination policy. 24.3.4. Unpleasant monetarist arithmetic. 24.3.5. An open market operation delivering neutrality. 24.3.6. The optimum quantity of money. 24.3.7. Legal restrictions to boost demand for currency. 24.3.8. One big open market operation. 24.3.9. A scal theory of the price level. 24.3.10. Exchange rate indeterminacy . 24.3.11. Determinacy of the exchange rate retrieved . 24.4. An example of exchange rate (in)determinacy. 24.4.1. Trading before sunspot realization. 24.4.2. Fiscal theory of the price level. 24.5. Optimal ination tax: the Friedman rule. 24.5.1. Economic environment. 24.5.2. Households optimization problem. 24.5.3. Ramsey plan. 24.6. Time consistency of monetary policy. 24.6.1. Model with monopolistically competitive wage setting. 24.6.2. Perfect foresight equilibrium. 24.6.3. Ramsey plan. 24.6.4. Credibility of the Friedman rule. 24.7. Concluding discussion. 24.8. Exercises.
25. Credit and Currency
25.1. Credit and currency with long-lived agents. 25.2. Preferences and endowments. 25.3. Complete markets. 25.3.1. A Pareto problem. 25.3.2. A complete markets equilibrium. 25.3.3. Ricardian proposition. 25.3.4. Loan market interpretation. 25.4. A monetary economy. 25.5. Townsends turnpike interpretation. 25.6. The Friedman rule. 25.6.1. Welfare. 25.7. Inationary nance. 25.8. Legal restrictions. 25.9. A two-money model. 25.10. A model of commodity money. 25.10.1. Equilibrium. 25.10.2. Virtue of at money. 25.11. Concluding remarks. 25.12. Exercises. 904 xvi Contents
26. Equilibrium Search and Matching 940
26.1. Introduction. 26.2. An island model. 26.2.1. A single market (island). 26.2.2. The aggregate economy. 26.3. A matching model. 26.3.1. A steady state. 26.3.2. Welfare analysis. 26.3.3. Size of the match surplus. 26.4. Matching model with heterogeneous jobs. 26.4.1. A steady state. 26.4.2. Welfare analysis. 26.4.3. The allocating role of wages I: separate markets. 26.4.4. The allocating role of wages II: wage announcements. 26.5. Model of employment lotteries . 26.6. Lotteries for households versus lotteries for rms. 26.6.1. An aggregate production function. 26.6.2. Time-varying capacity utilization. 26.7. Employment eects of layo taxes. 26.7.1. A model of employment lotteries with layo taxes. 26.7.2. An island model with layo taxes. 26.7.3. A matching model with layo taxes. 26.8. Kiyotaki-Wright search model of money. 26.8.1. Monetary equilibria. 26.8.2. Welfare. 26.9. Concluding comments. 26.10. Exercises.
Part VII: Technical appendixes
A. Functional Analysis 1005
A.1. Metric spaces and operators. A.2. Discounted dynamic programming. A.2.1. Policy improvement algorithm. A.2.2. A search problem.
B. Control and Filtering 1017
B.1. Introduction. B.2. The optimal linear regulator control problem. B.3. Converting a problem with cross products in states and controls to one with no such cross products. B.4. An example. B.5. The Kalman lter. B.6. Duality. B.7. Examples of Kalman ltering. B.8. Linear projections. B.9. Hidden Markov models. B.9.1.
Optimal ltering.
1. References 1044
2. Index 1072
3. Author Index 1077
4. Matlab Index 1082
Acknowledgments
_____________
簡易目次:
LS
Recursive Macroeconomic Theory 2nd EDITION
目次
Unformatted text preview: LARS LJUNGQVIST THOMAS J. SARGENT r ecursive macroeconomic theory SECOND EDITION Recursive Macroeconomic Theory 2nd.2004
Contents
Acknowledgements
Part I: The imperialism of recursive methods
1. Overview
Part II: Tools
2. Time Series
3. Dynamic Programming
4. Practical Dynamic Programming
5. Linear Quadratic Dynamic Programming
6. Search, Matching, and Unemployment
Part III: Competitive equilibria and applications
7. Recursive (Partial) Equilibrium
8. Equilibrium with Complete Markets
9. Overlapping Generations Models
10. Ricardian Equivalence
11. Fiscal Policies in the Growth Model
12. Recursive Competitive Equilibria
13. Asset Pricing
14. Economic Growth
15. Optimal Taxation with Commitment
Part IV: The savings problem and Bewley models
16. Self-Insurance
17. Incomplete Markets Models
Part V: Recursive contracts
18. Dynamic Stackelberg Problems
19. Insurance Versus Incentives
20. Equilibrium without Commitment ←第二版2004年から追加
21. Optimal Unemployment Insurance
22. Credible Government Policies
23. Two Topics in International Trade
Part VI: Classical monetary economics and search
24. Fiscal-Monetary Theories of Ination
25. Credit and Currency
26. Equilibrium Search and Matching
Part VII: Technical appendixes
References
Index
Acknowledgments
内容物
謝辞
パートI:再帰的な方法の帝国主義
1.概要
パートII:ツール
2.時系列
3.動的計画
4.実用的な動的計画
5.線形二次ダイナミック・プログラミング
6.検索、マッチング、失業
パートIII:競争均衡とアプリケーション
7.再帰的(部分的な)均衡
8.均衡 完全な市場
9.世代重複モデル
10.リカード等価
11.財政政策 成長モデル
12.再帰的な競争力の均衡
13.資産価格
14.経済成長
15.最適課税コミットメント
パートIV:貯蓄問題とビューリーズモデル
16.自己保険
17.不完全な市場モデル
パートV:再帰的な契約
18.ダイナミックケル問題
19.保険インセンティブ対
20.平衡コミットメントなし
21.最適失業保険
22.信頼できる政府の政策
23.国際貿易の二つのトピック
パートVI:クラシック金融経済学と検索
24.年度ネーションの金融理論
25.信用と通貨
26.均衡検索とマッチング
第VII部:技術の付録
参考文献
インデックス
謝辞
_______________________
第1版?(第二版と記載あり)2000簡易目次
http://www.econ.yale.edu/smith/econ510a/sargent3.pdf
Contents
Acknowledgements xvi
Preface xvii
Part I: The imperialism of recursive methods
1. Overview 1
Part II: Tools
2. Time series 24
3. Dynamic Programming 78
4. Practical Dynamic Programming 88
5. Linear Quadratic Dynamic Programming 101
6. Search, Matching, and Unemployment 131
Part III: Competitive equilibria and applications
7. Recursive (Partial) Equilibrium 178
8. Equilibrium with Complete Markets 194
9. Overlapping Generations Models 244
10. Ricardian Equivalence 290
11. Fiscal policies in the nonstochastic growth model 300
12. Recursive competitive equilibria 340
13. Asset Pricing 358
14. Economic Growth 411
15. Optimal Taxation with Commitment 441
Part IV: The savings problem and Bewley models
16. Self-Insurance 504
17. Incomplete Markets Models 524
Part V: Recursive contracts
18. Dynamic Stackelberg problems 571
19. Insurance Versus Incentives 590
20. Optimal unemployment insurance 671
21. Credible Government Policies 693
22. Two topics in international trade 740
Part VI: Classical monetary economics and search
23. Fiscal-Monetary Theories of Inflation 774
24. Credit and Currency 816
25. Equilibrium Search and Matching 854
Part VII: Technical appendixes
A. Functional Analysis 912
B.
26. References 949
27. Index 977
28. Author Index 983
29. Matlab Index 988
内容物謝辞のXVIはじめにxviiパートI:再帰的な方法の帝国主義1.概要1パートII:ツール2.時系列243.ダイナミック・プログラミング784.実用的な動的計画法885。線形二次ダイナミック・プログラミング1016.検索、マッチング、失業131パートIII:競争均衡とアプリケーション7.再帰的(部分的な)均衡1788。
完全な市場との均衡1949.世代重複モデル24410.リカード等価29011。非確率成長モデルにおける財政政策30012.再帰的な競争力の均衡34013.資産価格35814.経済成長41115。コミットメントと最適課税
441パートIV:貯蓄問題とビューリーズモデル16.自己保険50417.不完全な市場モデル524パートV:再帰的な契約18.ダイナミックケルの問題57119.保険インセンティブ590対20.最適失業保険67121.信頼できる政府の政策69322.国際貿易740で二つのトピックパートVI:クラシック金融経済学と検索23。
インフレ774の財政・金融理論24.信用と通貨81625.均衡検索と854のマッチング第VII部:技術の付録A.機能解析912B.26.参考文献94927.インデックス97728.著者索引98329. Matlabのインデックス988
__________________
詳細目次
書式なしテキストプレビュー:LARS LJUNGQVISTトーマスJ. S ARGENTはecursiveマクロ経済理論第二版再帰的マクロ経済理論第2版(2004年1st.2000)は、R
内容物
謝辞第二版のXVIIIの序文XVII
パートI:再帰的な方法の帝国主義
1.概要3
1.1。 警告。 1.2。 共通の祖先。 1.3。 貯蓄の問題。 1.3.1。 線形二次恒常所得理論。 1.3.2。 予備的貯蓄。 1.3.3。 市場、保険、富の分配を完了します。 1.3.4。 ビューリーズモデル。 1.3.5。 標準消費モデルで履歴依存性。 1.3.6。 成長理論。 1.3.7。 動的な最適課税の結果を制限します。 1.3.8。 資産価格。 1.3.9。 複数の資産。 1.4。 再帰的な方法。 1.4.1。 方法:動的プログラミングは、チャレンジを発行します。 1.4.2。 ダイナミックプログラミングが挑戦しました。 1.4.3。 動的計画法の帝国主義的応答。 1.4.4。 履歴依存性と動的なプログラミングが乗。 1.4.5。 ダイナミック主要なエージェントの問題。 1.4.6。 より多くのアプリケーション。 V VI目次
パートII:ツール
2.時系列29
2.1。 二つの主力。 2.2。 マルコフ連鎖。 2.2.1。 文房具分布。 2.2.2。 漸近定常。 2.2.3。 期待。 2.2.4。 機能を予測。 2.2.5。 不変の機能とエルゴード性。 2.2.6。 マルコフ連鎖をシミュレートします。 2.2.7。 尤度関数。 2.3。 Continuousstateマルコフ連鎖。 2.4。 確率的線形dierence方程式。 2.4.1。 第一及び第二の瞬間。 2.4.2。 インパルス応答関数。 2.4.3。 予測と割引。 2.4.4。 二次形式の幾何学的な和。 2.5。 人口回帰。 2.5.1。 スペクトル。 2.5.2。 例。 2.6。 例:LQ恒常所得モデル。 2.6.1。 不変部分空間アプローチ。 2.7。 金利の期間構造。 2.7.1。 確率的割引率。 2.7.2。 対数正規債券価格モデル。 2.7.3。 イールドカーブの傾きは、ログのmt + 1の系列相関に依存しています。 2.7.4。 バッカスとZins確率的割引率。 2.7.5。 確率的割引率をリバースエンジニアリング。 2.8。 推定。 2.9。 おわり。 A.線形dierence方程式。 2.11。 演習。
3.ダイナミック・プログラミング85
3.1。 シーケンシャル問題。 3.1.1。 三つの計算方法。 3.1.2。 コブ・ダグラス遷移、対数好み。 3.1.3。 オイラー方程式。 3.1.4。 サンプルオイラー方程式。 3.2。 確率制御問題。 3.3。 おわり。 3.4。 運動。
4.実用的な動的計画
4.1。 次元の呪い。 4.2。 状態空間の離散化。 4.3。 離散状態の動的計画。 4.4。 ハワード改善アルゴリズムの応用。 4.5。 数値実施。 4.5.1。 Modied政策反復。 4.6。 サンプルベルマン方程式。 4.6.1。 例1:期待効用を計算します。 4.6.2。 例2:リスクに敏感な好み。 4.6.3。 例3:ビジネスサイクルのコストを削減できます。 4.7。 多項式近似。 4.7.1。 推奨計算戦略。 4.7.2。 チェビシェフ多項式。 4.7.3。 アルゴリズム:概要。 4.7.4。 形状保存スプライン。 4.8。 おわり。 95目次
5.線形二次動的プログラミングVII 109
5.1。 導入。 5.2。 最適な線形レギュレータ問題。 5.2.1。 価値関数の繰り返し。 5.2.2。 割引リニアレギュレータ問題。 5.2.3。 ポリシー改善アルゴリズム。 5.3。 確率的に最適なリニア・レギュレータの問題。 5.3.1。 確実性等価の議論。 5.4。 リニア・レギュレータのシャドウ価格。 5.4.1。 安定。 5.5。 ラグランジュ法。 5.6。 カルマンLTER。 5.6.1。 Muths例。 5.6.2。 Jovanovics例。 5.7。 おわり。 A.マトリックス式。 B.線形二次近似。 5.B.1。 例:確率論的成長モデル。 5.B.2。 KydlandとPrescotts方法。 5.B.3。 Zの決意。 5.B.4。 線形近似を記録します。 5.B.5。 トレンド除去。 5.10¯。 演習。
6.検索、マッチング、失業139
6.1。 導入。 6.2。 予選。 6.2.1。 非負の確率変数。 6.2.2。 平均保存スプレッド。 6.3。 異時点間の就職のマッコールズモデル。 6.3.1。 平均保存スプレッドのEects。 6.3.2。 許可終了します。 6.3.3。 回を待っています。 6.3.4。 焼成。 6.4。 湖のモデル。 6.5。 職業選択のモデル。 6.6。 Jovanovicsマッチングモデルの簡易版。 6.6.1。 再帰的製剤およびソリューション。 6.6.2。 内因性の統計。 6.7。 Jovanovicsモデルの長い地平線バージョン。 6.7.1。 ベルマン方程式。 6.8。 おわり。 A.その他の数値動的計画。 6.A.1。 例4:検索。 6.A.2。 例5:ヨバノビッチモデル。 6.10。 演習。
パートIII:競争均衡とアプリケーション
7.再帰的(部分的な)均衡
7.1。 均衡概念。 7.2。 例:調整コスト。 7.2.1。 計画問題。 7.3。 再帰的な競争均衡。 7.4。 マルコフ完全均衡。 7.4.1。 計算。 7.5。 リニアマルコフ完璧な平衡。 7.5.1。 例。 7.6。 おわり。 7.7。 演習。 191 VIII内容
完全な市場208 8.平衡
8.1。 シーケンシャル取引時間対0。 8.2。 物理的な設定:好みや基金。 8.3。 代替取引の手配。 8.3.1。 履歴依存性。 8.4。 パレート問題。 8.4.1。 パレートの重みの時間不変。 8.5。 時間0取引:アロー・ドブリュー証券。 8.5.1。 均衡価格設定機能。 8.5.2。 均衡配分の最適。 8.5.3。 平衡計算。 8.5.4。 取引配置の解釈。 8.6。 例。 8.6.1。 例1:リスク分担。 8.6.2。 例2:いいえ集計不確実性。 8.6.3。 例3:定期的な寄付を処理します。 8.7。 資産価格の入門。 8.7.1。 冗長な資産価格設定。 8.7.2。 無リスク卓。 8.7.3。 無リスクのストリップ。 8.7.4。 テール資産。 8.7.5。 価格1周期に戻ります。 8.8。 シーケンシャル取引:アロー証券。 8.8.1。 証券を矢印。 8.8.2。 インサイト:内因性の状態変数として富。 8.8.3。 債務限度。 8.8.4。 シーケンシャル取引。 8.8.5。 割り当ての等価。 8.9。 再帰的な競争均衡。 8.9.1。 マルコフ過程によって支配基金。 8.9.2。 均衡の結果は、マルコフ性を継承します。 8.9.3。 最適化と均衡の再帰的製剤。 8.10。 J -step価格カーネル。 8.10.1。 アービトラージフリー価格。 8.11。 消費ストリップとビジネスサイクルのコスト。 8.11.1。 ビジネスサイクルコストへのリンク。 8.12。 ガウス資産価格モデル。 8.13。 パレート問題の再帰的なバージョン。 8.14。 貿易の静的モデル。 8.15。 閉鎖経済モデル。 8.15.1。 アウタルキー下に2つの国。 8.15.2。 福祉対策。 8.16。 自由貿易下に2つの国。 8.16.1。 小国の仮定。 8.17。 タリ。 8.17.1。 ナッシュタリ。 8.18。 おわり。 8.19。 演習。
9.世代重複モデル
9.1。 基金や好み。 9.2。 時間0取引。 9.2.1。 例平衡。 9.2.2。 福祉定理との関係。 9.2.3。 非定常均衡。 9.2.4。 コンピューティング平衡。 9.3。 シーケンシャル取引。 9.4。 お金。 9.4.1。 より均衡の計算。 9.4.2。 平衡の等価性。 9.5。 Decitンス。 9.5.1。 定常状態とラーアー曲線。 9.6。 同等のセットアップ。 9.6.1。 経済。 9.6.2。 成長。 9.7。 最適と金銭的均衡の存在。 9.7.1。 最適のためのBalaskoシェル基準。 9.8。 内世代異質。 9.8.1。 非貨幣均衡。 9.8.2。 金融均衡。 9.8.3。 非定常均衡。 9.8.4。 実際の手形の教義。 9.9。 贈答平衡。 9.10。 おわり。 9.11。 演習。 264目次
312 IX 10.リカードの等価
10.1。 借入限度とリカード等価。 10.2。 Innitelyエージェント経済に住んでいました。 10.2.1。 消費/貯蓄決定するソリューション。 10.3。 政府。 10.3.1。 家庭でEect。 10.4。 リンクされた世代の解釈。 10.5。 おわり。
成長モデル323 11.財政政策
11.1。 導入。 11.2。 経済。 11.2.1。 環境、技術、情報。 11.2.2。 競争均衡のコンポーネント。 11.2.3。 歪曲税と競争力の均衡。 11.2.4。 家庭:無裁定と資産価格決定式。 11.2.5。 資本式のユーザー・コスト。 11.2.6。 当社。 11.3。 コンピューティング平衡。 11.3.1。 非弾性労働供給。 11.3.2。 平衡定常状態。 11.3.3。 撮影アルゴリズムと平衡パスを計算します。 11.3.4。 他の平衡量。 11.3.5。 定常状態のR及びS / Q。 11.3.6。 一括税入手できます。 11.3.7。 ノー一括税が利用できます。 11.4。 バック解決に脱線。 11.5。 均衡配分と価格の税のEects。 11.6。 遷移実験。 11.7。 線形近似。 11.7.1。 λiをSとの関係。 11.7.2。 一度-と何でもジャンプ。 11.7.3。 式のSimplication。 11.7.4。 一回のパルス。 11.7.5。 収束速度と期待速度。 11.8。 弾性労働供給。 11.8.1。 定常状態計算。 11.8.2。 精度に余談:オイラー方程式エラー。 11.9。 成長。 11.10。 おわり。 A.ログ線形近似。 11.12。 演習。
12.再帰的な競争力の均衡
12.1。 内因性集合状態変数。 12.2。 確率的成長モデル。 12.3。 計画問題のラグランジュ法。 12.4。 時間0取引:アロー・ドブリュー証券。 12.4.1。 家庭。 12.4.2。 I型12.4.3の事務所。 II型の事務所。 12.4.4。 均衡価格と数量。 12.4.5。 暗黙の富のダイナミクス。 12.5。 シーケンシャル取引:アロー証券。 12.5.1。 家庭。 12.5.2。 I型12.5.3の事務所。 II型の事務所。 12.5.4。 均衡価格と数量。 12.5.5。 II型RMを融資。 12.6。 再帰的製剤。 12.6.1。 技術は、マルコフ過程によって支配されます。 12.6.2。 経済の集合状態。 12.7。 計画問題の再帰的製剤。 12.8。 シーケンシャル取引の再帰的製剤。 12.8.1。 ビッグK、K少しトリック。 12.8.2。 価格システム。 12.8.3。 家庭の問題。 12.8.4。 I型12.8.5の事務所。 II型の事務所。 12.9。 再帰的な競争均衡。 366 X 12.9.1内容。 決定ルール全体の均衡の制限。 12.9.2。 計画問題を用いて。 12.10。 おわり。
13.資産価格392
13.1。 導入。 13.2。 資産オイラー方程式。 13.3。 消費と株価のマーチンゲール理論。 13.4。 同値マルチンゲール測度。 13.5。 均衡資産価格。 13.6。 泡なしの株価。 13.7。 資産価格を計算します。 13.7.1。 例1:対数好み。 13.7.2。 例2:有限状態のバージョン。 13.7.3。 例3:成長と資産価格。 13.8。 金利の期間構造。 13.9。 状態依存的な価格。 13.9.1。 保険料。 13.9.2。 人工の不確実性。 13.9.3。 MM定理。 13.10。 政府の借金。 13.10.1。 リカードの命題。 13.10.2。 いいえポンジースキームません。 13.11。 リスク回避度パラメータの解釈。 13.12。 株式プレミアムパズル。 13.13。 リスクの市場価格。 13.14。 HansenJagannathan境界です。 13.14.1。 価格カーネルの内積表現。 13.14.2。 確率的割引因子のクラス。 13.14.3。 ハンセン-Jagannathanが結合しました。 13.14.4。 Mehra-プレスコットデータ。 13.15。 ファクターモデル。 13.16。 異質性と不完全な市場。 13.17。 おわり。 13.18。 演習。
14.経済成長449
14.1。 導入。 14.2。 経済。 14.2.1。 バランスのとれた成長経路。 14.3。 外因性成長。 14.4。 波及効果の外部性。 14.5。 再現性のあるすべての要因。 14.5.1。 ワンセクター・モデル。 14.5.2。 二部門モデル。 14.6。 研究独占的競争。 14.6.1。 独占的競争の結果。 14.6.2。 プランナーソリューション。 14.7。 再現不能な要因にもかかわらず成長。 14.7.1。 資本財のコアは再現不能の入力なしで製造。 14.7.2。 外部性を楽しんで研究労働。 14.8。 コメントを締結。 14.9。 演習。
コミットメント15.最適課税
15.1。 導入。 15.2。 非確率経済。 15.2.1。 政府。 15.2.2。 世帯。 15.2.3。 企業。 15.3。 ラムゼイルール。 15.4。 ゼロ資本税。 15.5。 再配布に制限します。 15.6。 ラムゼイルールにプライマルアプローチ。 15.6.1。 ラムジープランを構築。 15.6.2。 ゼロ資本税を再訪。 15.7。 初期投資の課税。 15.8。 不完全な課税のためにゼロ以外の資本税。 15.9。 確率的経済。 15.9.1。 政府。 15.9.2。 世帯。 15.9.3。 企業。 478内容は15.10をXI。 状態偶発負債と資本税の不確定性。 15.11。 不確実性の下でラムジー計画。 15.12。 事前の資本税はゼロの周りに変化します。 15.12.1。 命題2 15.13の証明のスケッチ。 労働税の平滑化の例。 15.13.1。 例1:GT = G全てのT 0のため。 15.13.2。 例2:GT = 0、T = T、およびGT> 0のため。 15.13.3。 例3:tの場合= 0、GT = T、およびGTは確率的です。 15.14。 最適な負債政策への教訓。 15.15。 状態偶発債務なしで課税。 15.15.1。 {GT}の将来値が確定的になります。 15.15.2。 確率{GT}が、特別な設定。 15.15.3。 例3は、再訪:GT tに対して= 0 = T、およびGTは確率的です。 15.16。 人的資本のゼロ税。 15.17。 すべての税金はゼロであるべき? 15.18。 おわり。 15.19。 演習。 パートIV:貯蓄問題とビューリーズモデル
16.自己保険545
16.1。 導入。 16.2。 消費者の環境。 16.3。 非確率寄付。 16.3.1。 アドホック借入制約:非負の資産。 16.3.2。 例:定期的な寄付プロセス。 16.4。 二次好み。 16.5。 確率的養老プロセス:IID場合。 16.6。 確率的養老プロセス:一般的なケース。 16.7。 経済直感。 16.8。 おわり。 A. Supermartingale収束定理。 16.10。 演習。
17.不完全な市場モデル
17.1。 導入。 17.2。 貯蓄の問題。 17.2.1。 富雇用分布。 17.2.2。 分布λの再解釈。 17.2.3。 例1:純粋な信用モデル。 17.2.4。 平衡計算。 17.2.5。 例2:資本金を持つモデル。 17.2.6。 平衡の計算。 17.3。 Unication、さらに分析します。 17.4。 余談:非確率貯蓄問題。 17.5。 借入限度:自然とアドホック。 17.5.1。 単一の状態変数の候補。 17.5.2。 再び収束をSupermartingale。 17.6。 rの関数としての平均資産。 17.7。 計算例。 17.8。 いくつかのビューリーズモデル。 17.8.1。 最適な静止割り当て。 17.9。 資本と民間のIOUを持つモデル。 17.10。 プライベートIOUのだけ。 17.10.1。 何信用の制限を達成することができます。 17.10.2。 ρrとの近接。 17.10.3。 インサイドお金や自由な銀行の解釈。 17.10.4。 お金でのビューリーズ基本モデル。 17.11。 シニョレッジのモデル。 17.12。 為替レートの不確定。 17.12.1。 566 XII目次通貨の金利。 17.12.2。 明示的な関心。 17.12.3。 Mの上限。 p 17.12.4。 非常に特殊なケース。 17.12.5。 deationを通じて利子。 17.13。 予備的貯蓄。 17.14。 集計変数をuctuating付きモデル。 17.14.1。 再びAiyagarisモデル。 17.14.2。 Krusellとスミス延長。 17.15。 おわり。 17.16。 演習。
パートV:再帰的な契約
18.ダイナミックケル問題615
18.1。 履歴依存性。 18.2。 ケルの問題。 18.3。 シュタッケルベルクの問題を解決します。 18.3.1。 ステップ1:最適なリニア・レギュレータを解決します。 18.3.2。 ステップ2:影の価格PのYTの安定化特性を使用しています。 18.3.3。 溶液を安定化させます。 18.3.4。 ステップ3:実施乗数を変換します。 18.3.5。 決定ルールの履歴依存表現。 18.3.6。 均衡の決定性に余談。 18.4。 競争力のフリンジを持つ大規模なRM。 18.4.1。 競争力のフリンジ。 18.4.2。 独占の問題。 18.4.3。 平衡表現。 18.4.4。 数値例。 18.5。 おわり。 A.安定μT= PのYTに。 B.マトリックス線形dierence方程式。 C.は、数式を予測します。 18.9。 演習。
19.保険インセンティブ対
19.1。 再帰的な契約を結んでいる保険。 19.2。 基本的な環境。 19.3。 何のコミットメントを片側ません。 19.3.1。 自己強制契約。 19.3.2。 再帰的製剤およびソリューション。 19.3.3。 契約の再帰的計算。 19.3.4。 Prots。 19.3.5。 P(V)は、厳密に凹と連続dierentiableです。 19.3.6。 多くの世帯。 19.3.7。 例。 19.4。 ラグランジュの方法。 19.5。 非対称情報と保険。 19.5.1。 EciencyはBS1のBS、WS1 WSを意味します。 19.5.2。 ローカル上下制約が十分にあります。 19.5.3。 Pの陥凹。 19.5.4。 ローカル下向きの制約は、常にバインド。 19.5.5。 共同保険。 19.5.6。 P(V)がマルチンゲールです。 19.5.7。 コミットメント問題をモデル化するための比較。 19.5.8。 継続値を拡散。 19.5.9。 マーチンゲール収束と貧困。 19.5.10。 一般均衡への拡張。 19.5.11。 自己保険との比較。 19.6。 観察不能なストレージと保険。 19.6.1。 フィージビリティ。 19.6.2。 インセンティブの互換性。 19.6.3。 Ecient割り当て。 19.6.4。 2つの期間(T = 2)の場合。 19.6.5。 プランナーの役割。 19.6.6。 636目次XIIIにおける地方分権化は経済を閉じました。 19.7。 おわり。 A.歴史的発展。 19.A.1。 スピアとSrivastava氏。 19.A.2。 タイミング。 19.A.3。 宝くじの使用。 19.9。 演習。
コミットメント697なし20均衡
20.1。 コミットメントの両面欠如。 20.2。 クローズドシステム。 20.3。 再帰的製剤。 20.4。 平衡消費。 20.4.1。 消費ダイナミクス。 20.4.2。 消費間隔はお互いを含めることはできません。 20.4.3。 基金は、消費間隔に含まれています。 20.4.4。 (アウタルキーが唯一の持続可能な割り当てでない限り)すべての消費間隔が非縮退しています。 20.5。 パレートフロンティアと利益の事前部門。 20.6。 消費分布。 20.6.1。 漸近分布。 20.6.2。 一時的な不完全なリスク分担。 20.6.3。 パーマネント不完全なリスク分担。 20.7。 代替再帰的製剤。 20.8。 パレートフロンティアを再訪します。 20.8.1。 値は、暗黙的な消費で連続しています。 20.8.2。 パレートフロンティアのDierentiability。 20.9。 継続はラKocherlakota値。 20.9.1。 漸近分布は、 `(ときS = 2を除く)不完全なリスク・シェアリングのための非退化です。 20.9.2。 継続値は、常に参加制約を結合に応答しません。 20.10。 二状態例:記憶喪失、メモリを圧倒する。 20.10.1。 パレートフロンティア。 20.10.2。 解釈。 20.11。 スリーステート例。 20.11.1。 パラメータ値の摂動。 20.11.2。 パレートフロンティア。 20.12。 実証的動機。 20.13。 汎化。 20.14。 地方分権。 20.15。 内因性借入制約。 20.16。 おわり。 20.17。 演習。
21.最適失業保険
21.1。 履歴依存失業保険。 21.2。 ワンスペルモデル。 21.2.1。 アウタルキー問題。 21.2.2。 完全な情報と失業保険。 21.2.3。 インセンティブ問題。 21.2.4。 情報の非対称性と失業保険。 21.2.5。 計算例。 21.2.6。 計算の詳細。 21.2.7。 解釈。 21.2.8。 拡張:オン・ザ・ジョブ税。 21.2.9。 拡張:断続的な失業呪文。 21.3。 生涯契約を結んで複数のスペルモデル。 21.3.1。 セットアップ。 21.3.2。 再帰的な生涯契約。 21.3.3。 報酬ダイナミクスとき失業者。 21.3.4。 報酬ダイナミクスを採用しています。 21.3.5。 概要。 21.4。 おわり。 21.5。 演習。 751 XIV内容
22.信頼できる政府の政策773
22.1。 導入。 22.2。 ダイナミックプログラミングは乗:概要を。 22.3。 1周期経済。 22.3.1。 競争均衡。 22.3.2。 ラムゼイルール。 22.3.3。 ナッシュ均衡。 22.4。 経済の例。 22.4.1。 課税例。 22.4.2。 離散選択セットを持つブラックボックスの例。 22.5。 評判のメカニズム:一般的な考え。 22.5.1。 ダイナミックプログラミングは二乗しました。 22.6。 innitely繰り返し経済。 22.6.1。 戦略PROLE歴史と価値を意味します。 22.6.2。 再帰的製剤。 22.7。 完全均衡(SPE)をサブゲーム。 22.8。 SPEの例。 22.8.1。 1周期ナッシュ均衡のInnite繰り返し。 22.8.2。 トリガー戦略とのより良い成果をサポートします。 22.8.3。 ナッシュへの復帰は十分に悪いわけではないとき。 22.9。 すべてのSPEの値。 22.9.1。 動的プログラミングの基本的な考え方は、乗。 22.10。 自己強制SPE。 22.10.1。 ナッシュ結果の繰り返しよりも悪い何かのための探求。 22.11。 再帰的な戦略。 22.12。 再帰的な戦略とSPEの例。 22.12.1。 ナッシュ結果のInnite繰り返し。 22.12.2。 良いナッシュ結果のInnite繰り返し。 22.12.3。 さらに悪い何か:スティック・アンド・ニンジン戦略。 22.13。 最良と最悪のSPE値。 22.13.1。 V1は候補セットの外にある場合。 22.14。 例:最悪の事態を達成するための代替方法。 22.14.1。 最悪の場合、この方法1. 22.14.2を実現。 最悪の場合、方法2 22.14.3を実現。 最悪の場合、方法3 22.14.4を実現。 数値例。 22.15。 解釈。 22.16。 おわり。 22.17。 演習。
23.国際貿易の二つのトピック
23.1。 2つのダイナミック請負問題。 23.2。 モラルハザードとdicult執行で貸出。 23.2.1。 アウタルキー。 23.2.2。 完全保険と投資。 23.2.3。 限定コミットメントと観測されない投資。 23.2.4。 最適な資本は苦痛の下outows。 23.3。 貿易政策における漸進主義。 23.3.1。 クローズド・経済モデル。 23.3.2。 自由貿易の下で、両国のリカードモデル。 23.3.3。 タリとの貿易。 23.3.4。 福祉・ナッシュタリ。 23.3.5。 貿易譲歩。 23.3.6。 繰り返しタリゲーム。 23.3.7。 時間不変転送。 23.3.8。 漸進主義:時間的に変化する貿易政策。 23.3.9。 ベースラインポリシー。 23.3.10。 payosと継続値の多重度。 23.4。 おわり。 AtkesonsモデルのA.計算。 23.6。 演習。 クラシック金融経済学と検索:820内容はパートVIをXV
ネーション857の24年度、金融理論
24.1。 問題。 24.2。 ショッピング時間貨幣経済。 24.2.1。 世帯。 24.2.2。 政府。 24.2.3。 平衡。 24.2.4。 長期対短期。 24.2.5。 定常均衡。 24.2.6。 最初の日付(時間0)。 24.2.7。 平衡決意。 24.3。 テン金銭的教義。 24.3.1。 貨幣数量説。 24.3.2。 持続decitsはネーションの原因となります。 24.3.3。 ゼロネーション政策の財政の前提条件。 24.3.4。 不快なマネタリスト演算。 24.3.5。 公開市場操作は、中立性を実現します。 24.3.6。 お金の最適量。 24.3.7。 通貨の需要を後押しする法的規制。 24.3.8。 一つの大きなオープン市場操作。 24.3.9。 物価水準の年度理論。 24.3.10。 為替レートの不確定。 24.3.11。 検索された為替レートの決定性。 24.4。 為替レート(中)決定性の例。 24.4.1。 太陽黒点の実現の前に取引。 24.4.2。 物価水準の財政理論。 24.5。 最適ネーション税:フリードマン・ルール。 24.5.1。 経済環境。 24.5.2。 家計の最適化問題。 24.5.3。 ラムジー計画。 24.6。 金融政策の時間の一貫性。 24.6.1。 独占的競争賃金が設定されたモデル。 24.6.2。 完全予見均衡。 24.6.3。 ラムジー計画。 24.6.4。 フリードマン・ルールの信頼性。 24.7。 議論を総括。 24.8。 演習。
25.信用と通貨
25.1。 長寿命の薬と信用と通貨。 25.2。 設定と基金。 25.3。 完全な市場。 25.3.1。 パレート問題。 25.3.2。 完全な市場の均衡。 25.3.3。 リカードの命題。 25.3.4。 ローン市場の解釈。 25.4。 貨幣経済。 25.5。 Townsendsは解釈をターンパイク。 25.6。 フリードマン・ルール。 25.6.1。 福祉。 25.7。 Inationaryンス。 25.8。 法的規制。 25.9。 2マネー・モデル。 25.10。 商品金のモデル。 25.10.1。 平衡。 25.10.2。 お金での美徳。 25.11。 おわり。 25.12。 演習。 904 XVIの内容
26.均衡検索と940のマッチング
26.1。 導入。 26.2。 島モデル。 26.2.1。 単一市場(島)。 26.2.2。 集計経済。 26.3。 マッチングモデル。 26.3.1。 定常状態。 26.3.2。 厚生分析。 26.3.3。 試合黒字のサイズ。 26.4。 異種の仕事でモデルをマッチング。 26.4.1。 定常状態。 26.4.2。 厚生分析。 26.4.3。 独立した市場:賃金私の割り当て役割。 26.4.4。 賃金IIの割り当て役割:賃金発表。 26.5。 雇用宝くじのモデル。 26.6。 RMSの宝くじ対世帯宝くじ。 26.6.1。 集計生産関数。 26.6.2。 時変の稼働率。 26.7。 layo税の雇用eects。 26.7.1。 layo税と雇用宝くじのモデル。 26.7.2。 layo税と島モデル。 26.7.3。 layo税とのマッチングモデル。 26.8。 お金の清滝・ライトの検索モデル。 26.8.1。 金融平衡。 26.8.2。 福祉。 26.9。 コメントを締結。 26.10。 演習。
第VII部:技術の付録
A.機能解析1005
A.1。 距離空間と演算子。 A.2。 割引動的計画。 A.2.1。 ポリシー改善アルゴリズム。 A.2.2。 探索問題。
B.コントロールとフィルタリング1017
B.1。 導入。 B.2。 最適なリニア・レギュレータの制御の問題。 B.3。 そのようなクロス製品と一つにクロス状態で製品とコントロールの問題を変換します。 B.4。 例。 B.5。 カルマンLTER。 B.6。 双対性。 B.7。 カルマンlteringの例。 B.8。 線状突起。 B.9。 隠れマルコフモデル。 B.9.1。
最適ltering。
1.参照1044
2.インデックス1072
3.著者索引1077
4. Matlabのインデックス1082
謝辞
以下引用。
////////
RIETI - 「期待」どこまで解明?
小林慶一郎
http://www.rieti.go.jp/jp/papers/contribution/kobayashi/50.html
////////
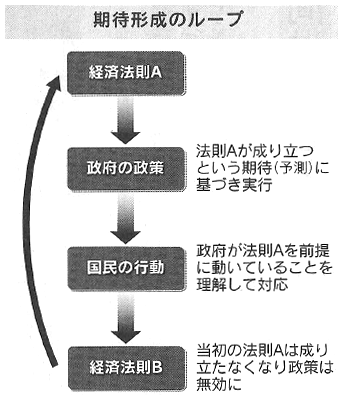
↑ 筆者注、こんなものができると思いますか????? なぜ、従来モデルに、こんなものを取り入れれば「実践に耐えるモデル」になるなど、夢物語を語るのでしょうか、経済学者は? 小林慶一郎「『期待』どこまで解明?」日経経済教室 H25.10.21 …合理的期待の本質は経済における期待が「自己言及性」を持つという点…、自己言及性とは、期待が巡り巡って自分自身(期待)を決める性質のことである。 では、解説します。 ルーカス批判です。 「インフレは家計に賃金が増えて豊かになったと錯覚を起こさせ、消費を増やす」 について、 政府が景気を良くしようとインフレを起こしても、「国民はその意図を知っているので、インフレに備えて消費を減らす」→その結果、「インフレでも消費は増えない」とするものです。 「期待(筆者注:誤訳で、本当は「予想」のこと)に基づき行動すると、結果的に「期待(予測)」そのものも、変わる」これが、「自己言及性」です。 だから、経済法則なんて、いつまでたっても、「本当は決まらない」のです。 ところが、これを「動かない」と仮定させます。「家計や企業は、完全情報を持ち、合理的に行動する」とするのです。
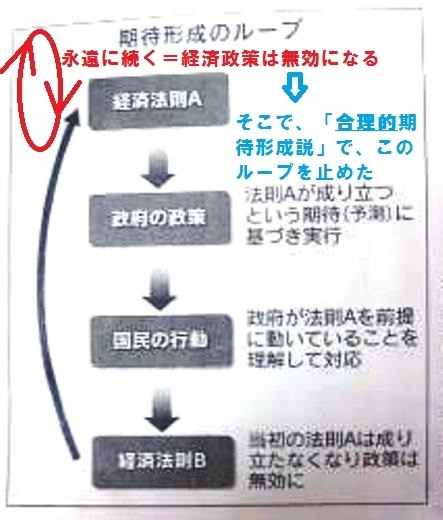 経済学は、これを「合理的期待(予想)」と名付け、「仮定」させて、自分たちの理論を展開(これなら簡単です)、正当化させてきたのです。 こんなもの、そもそも成り立ちません。 で、大学院レベル(例:トーマス・サージェント『再帰的マクロ経済理論』)では、「自己言及性」に「再帰」しようと試みています。ですが、そこでもまだ、非現実的な仮定が、使われ続けています。 過去10年、中央銀行がモデルとして使ってきた、動学的確率的一般均衡:DSGEも同じです。「家計や企業は合理的・・・しかもすべての家計や企業」です。そうすると、景気変動も「合理的」となり、不況さえ、家計や企業にとって「最適」という結論になります。 だから、リーマン・ショックを前に、このモデルでは、歯が立たないのです。DSGEモデルでは、不況克服ではなく、「価格の自由自在な伸縮による効率性」しか、追及できないのです。 これを克服する動きとして、米プリンストン大学の清滝宏教授と英ロンドン・スクール・オブ・エコノミクスのジョン・ムーア教授の12年の論文のように合理的期待の仮定を維持したまま、異質な経済主体の相互作用を分析…。 …シカゴ大のラース・ハンセン教授…「経済の真の構造が分からない」という条件下で、経済法則を推測する…。 …どれも合理的期待仮説の本質(筆者注:動かないと仮定)を覆すものではない。…マクロ経済学に決定打はまだない。 「まだない」のではなく、そんなもの、「あり得ない=存在できず=不可能」なのです。 70億人の行動を「予想」することは、永遠に不可能ですし、1人/70億人(ミクロ)をいくら研究しても、70億人からなるマクロ経済は、分析できません。 吉川洋『過去40年間のマクロ経済学は間違った路線だった』週刊エコノミスト13.9.10号 …ルーカス理論の一番の問題は、特定の資産市場には有効かもしれない合理的期待の概念を、労働市場や賃金といったマクロ経済に無反省に適用したことだ。マクロ経済では、家計や企業などミクロの経済主体はそれぞれ異なる世界で行動している。一つの「マクロ経済」を共有していない。 …代表的な企業や家計の行動をそう相似拡大し…日本国内の「ザ・企業」と「ザ・家計」という二つの経済主体を相手に…だがそもそもこんなモデルを誰も正しいとは思わないだろう。
経済学は、これを「合理的期待(予想)」と名付け、「仮定」させて、自分たちの理論を展開(これなら簡単です)、正当化させてきたのです。 こんなもの、そもそも成り立ちません。 で、大学院レベル(例:トーマス・サージェント『再帰的マクロ経済理論』)では、「自己言及性」に「再帰」しようと試みています。ですが、そこでもまだ、非現実的な仮定が、使われ続けています。 過去10年、中央銀行がモデルとして使ってきた、動学的確率的一般均衡:DSGEも同じです。「家計や企業は合理的・・・しかもすべての家計や企業」です。そうすると、景気変動も「合理的」となり、不況さえ、家計や企業にとって「最適」という結論になります。 だから、リーマン・ショックを前に、このモデルでは、歯が立たないのです。DSGEモデルでは、不況克服ではなく、「価格の自由自在な伸縮による効率性」しか、追及できないのです。 これを克服する動きとして、米プリンストン大学の清滝宏教授と英ロンドン・スクール・オブ・エコノミクスのジョン・ムーア教授の12年の論文のように合理的期待の仮定を維持したまま、異質な経済主体の相互作用を分析…。 …シカゴ大のラース・ハンセン教授…「経済の真の構造が分からない」という条件下で、経済法則を推測する…。 …どれも合理的期待仮説の本質(筆者注:動かないと仮定)を覆すものではない。…マクロ経済学に決定打はまだない。 「まだない」のではなく、そんなもの、「あり得ない=存在できず=不可能」なのです。 70億人の行動を「予想」することは、永遠に不可能ですし、1人/70億人(ミクロ)をいくら研究しても、70億人からなるマクロ経済は、分析できません。 吉川洋『過去40年間のマクロ経済学は間違った路線だった』週刊エコノミスト13.9.10号 …ルーカス理論の一番の問題は、特定の資産市場には有効かもしれない合理的期待の概念を、労働市場や賃金といったマクロ経済に無反省に適用したことだ。マクロ経済では、家計や企業などミクロの経済主体はそれぞれ異なる世界で行動している。一つの「マクロ経済」を共有していない。 …代表的な企業や家計の行動をそう相似拡大し…日本国内の「ザ・企業」と「ザ・家計」という二つの経済主体を相手に…だがそもそもこんなモデルを誰も正しいとは思わないだろう。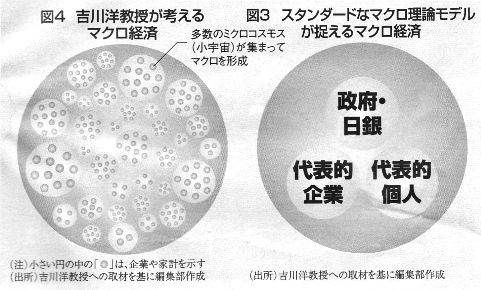 …マクロ経済を代表的な経済主体の動きでとらえるモデルでは、経済主体が合理的である限り…適当な変数を動かせば、期待をどのようにでも動かせる。しかし、そんなモデルに意味があるのか。 …自然科学の分野…多数のミクロが集まったマクロ系の分析…では個々のミクロの動きを追っても意味がないとしている。ミクロの動きはばらばらでわからないからだ。 …一つの部屋。この部屋のマクロ…温度を調べるために、一つの代表的な酸素を選び出し、それを詳しく調べても何の意味もない。 …マクロは、「ミクロの動きを抑えることが基本」と、代表的企業、代表的家計を想定して、マクロはその相似拡大としてきた。…酸素の動きを通して部屋の状態(マクロ)を理解しようとしているのと同じだ。こうした方法論は間違っている。ミクロとマクロは別、昔の二刀流(筆者注:新古典派のミクロ経済学とケインズ経済学の共存)が正しい…。 ロバート・J・シラー 「数字より結果重視?経済学は『科学』なのか」週刊東洋経済H25.11.23 p116 …経済学の問題の一つは、どうしても基本原理の発見よりも政策に焦点を合わせるということだ。…経済政策に焦点を合わせると、科学でないことが多くかかわってくることだ。政治が関与し始め、政治的なジェスチャーが人々の注目という見返りを受ける。 「新自由主義」「市場原理主義」など、経済学にはない概念を作り出し、「小泉改革」で格差が拡大したなど、本当に科学(事実)とちがう物語が作られます。そのエセ事実が拡散します。 …「科学」とつけるのは、評判の悪い類縁と区別をつけるためだ。 …「政治科学(政治学)」という用語…真実の追求よりも影響力の行使や票の確保を目当てにした…小冊子から一線を画した。 …「天文科学」…占星術や星座に関する古代神話の研究と区別しようとしたものだ。 …「天文科学」…20世紀…ほぼ消滅した。 それらの用語も、徐々に消えてなくなります。 …「化学科学」という用語…19世紀…錬金術や怪しい特効薬作りと一線を画そうとしていた。…真の科学と疑似科学を区別する…この用語を使う必要は1901年にノーベル賞が創設された頃までにほぼなくなっていた。 …「天文科学」…20世紀…ほぼ消滅した。…占星術…星が私たちの運命を決めるという考え方は、知的にはまったく通用しなくなった。…「天文科学」という用語は必要なくなった。 さて、経済学です。 …「経済科学」を批判する人々は…難解な数字を見せびらかすだけの「疑似科学」の発展だ、と指摘している。…「統制された実験などないので、誰にも暴けない」…。 シラー教授は言います。 …妥当性が明らかになることがないモデルに対して経済学のほうが物理科学よりもいくぶん脆弱だ。 え?「いくぶん」ですか? …というのは、経済学モデルは人間を対象としており、近似の必要性が物理科学の場合よりもずっと高い。 近似(似ている)が必要だ。対象が、「何をしでかすかわからない人間」だからです。CO2とか、真空なら、理論通りですが、何しろ相手が「気まぐれ」な人間です。CO2を対象とした理論・実験のように「静止」してくれません。 …人間は気持ちが変わりやすく、まったく違った振る舞いをすることがある。神経症やアイデンティティの問題を持つ人もおり…。 このような、「ヒト」というものを対象にする限り、「普遍妥当性」を求める科学など、土台、成立しません。 …複雑な現象が経済成果を理解することと関係があると行動経済学の分野で分かりつつある。 …単純化できない経済の人間的要素に合ったモデル(筆者補足:DSGEモデルなど)を作るために必要な調整と、数学的洞察を結合させるのは課題のままだ。 課題のままですか・・・そんなもの、永遠に課題のままで、整合性は取れないのです。普遍的妥当性など、経済学には無理なのです。 …行動経済学の進歩は…現在はやりの数学的な経済モデル(筆者補足DSGEモデル)の一部と矛盾する可能性はある。そして経済学はそれ自体の方法論上の問題を抱えている…。 矛盾する可能性・・・矛盾ばかりです。なぜかと言うと、前提(ここが経済学の致命傷)が違うので、絶対に交わることができないのです。 ミクロ経済学では、ヒトは合理的だというのが「前提」です。 清水書院 新政治・経済 p93 平成21年 三版
…マクロ経済を代表的な経済主体の動きでとらえるモデルでは、経済主体が合理的である限り…適当な変数を動かせば、期待をどのようにでも動かせる。しかし、そんなモデルに意味があるのか。 …自然科学の分野…多数のミクロが集まったマクロ系の分析…では個々のミクロの動きを追っても意味がないとしている。ミクロの動きはばらばらでわからないからだ。 …一つの部屋。この部屋のマクロ…温度を調べるために、一つの代表的な酸素を選び出し、それを詳しく調べても何の意味もない。 …マクロは、「ミクロの動きを抑えることが基本」と、代表的企業、代表的家計を想定して、マクロはその相似拡大としてきた。…酸素の動きを通して部屋の状態(マクロ)を理解しようとしているのと同じだ。こうした方法論は間違っている。ミクロとマクロは別、昔の二刀流(筆者注:新古典派のミクロ経済学とケインズ経済学の共存)が正しい…。 ロバート・J・シラー 「数字より結果重視?経済学は『科学』なのか」週刊東洋経済H25.11.23 p116 …経済学の問題の一つは、どうしても基本原理の発見よりも政策に焦点を合わせるということだ。…経済政策に焦点を合わせると、科学でないことが多くかかわってくることだ。政治が関与し始め、政治的なジェスチャーが人々の注目という見返りを受ける。 「新自由主義」「市場原理主義」など、経済学にはない概念を作り出し、「小泉改革」で格差が拡大したなど、本当に科学(事実)とちがう物語が作られます。そのエセ事実が拡散します。 …「科学」とつけるのは、評判の悪い類縁と区別をつけるためだ。 …「政治科学(政治学)」という用語…真実の追求よりも影響力の行使や票の確保を目当てにした…小冊子から一線を画した。 …「天文科学」…占星術や星座に関する古代神話の研究と区別しようとしたものだ。 …「天文科学」…20世紀…ほぼ消滅した。 それらの用語も、徐々に消えてなくなります。 …「化学科学」という用語…19世紀…錬金術や怪しい特効薬作りと一線を画そうとしていた。…真の科学と疑似科学を区別する…この用語を使う必要は1901年にノーベル賞が創設された頃までにほぼなくなっていた。 …「天文科学」…20世紀…ほぼ消滅した。…占星術…星が私たちの運命を決めるという考え方は、知的にはまったく通用しなくなった。…「天文科学」という用語は必要なくなった。 さて、経済学です。 …「経済科学」を批判する人々は…難解な数字を見せびらかすだけの「疑似科学」の発展だ、と指摘している。…「統制された実験などないので、誰にも暴けない」…。 シラー教授は言います。 …妥当性が明らかになることがないモデルに対して経済学のほうが物理科学よりもいくぶん脆弱だ。 え?「いくぶん」ですか? …というのは、経済学モデルは人間を対象としており、近似の必要性が物理科学の場合よりもずっと高い。 近似(似ている)が必要だ。対象が、「何をしでかすかわからない人間」だからです。CO2とか、真空なら、理論通りですが、何しろ相手が「気まぐれ」な人間です。CO2を対象とした理論・実験のように「静止」してくれません。 …人間は気持ちが変わりやすく、まったく違った振る舞いをすることがある。神経症やアイデンティティの問題を持つ人もおり…。 このような、「ヒト」というものを対象にする限り、「普遍妥当性」を求める科学など、土台、成立しません。 …複雑な現象が経済成果を理解することと関係があると行動経済学の分野で分かりつつある。 …単純化できない経済の人間的要素に合ったモデル(筆者補足:DSGEモデルなど)を作るために必要な調整と、数学的洞察を結合させるのは課題のままだ。 課題のままですか・・・そんなもの、永遠に課題のままで、整合性は取れないのです。普遍的妥当性など、経済学には無理なのです。 …行動経済学の進歩は…現在はやりの数学的な経済モデル(筆者補足DSGEモデル)の一部と矛盾する可能性はある。そして経済学はそれ自体の方法論上の問題を抱えている…。 矛盾する可能性・・・矛盾ばかりです。なぜかと言うと、前提(ここが経済学の致命傷)が違うので、絶対に交わることができないのです。 ミクロ経済学では、ヒトは合理的だというのが「前提」です。 清水書院 新政治・経済 p93 平成21年 三版 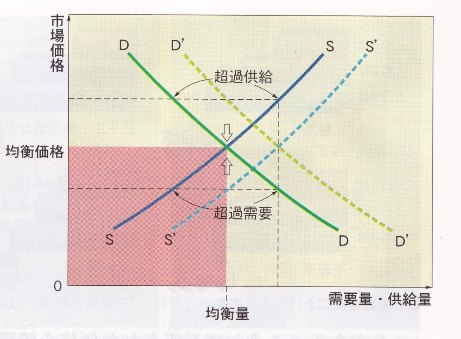 おなじみの、中学校の教科書にさえ掲載されている、経済学の基礎の基礎、「供給・需要」曲線が成立するには、箱庭のような条件が必要です。 (1)財・サービスの内容について完全に知っている、無数の消費者 (2)財・サービスの内容について完全に知っている、無数の生産者 (3)完全競争市場であること(寡占・独占やカルテルを結ばない) (4)消費者は、効用を最大限にするように行動する (5)生産者は利益を最大限にするように行動する ミクロ経済学を基礎にしたマクロ経済学は、この前提を継承します。 池田和人「連続講義・デフレと経済政策―アベノミクスの経済分析」 ・・・1982年、キッドランドとプレスコットが・・・これまで述べてきたような要素を持ったマクロ経済学モデル・・・を示しました。・・・動学的で確率論なモデルです。・・・各時点ですべての市場で需要と供給が一致(均衡)が達成されていると想定され・・・動学的(dynamic)で確率論的(stochastic)な一般均衡(general equilibrium)モデル・・・DSGEと呼ばれるモデル群の先駆けです。 ところが、行動経済学では、ヒトは不合理ではないか?を前提とします。 山岡 道男, 浅野 忠克「ガブッ!とわかる世界一やさしい行動経済学の教室」 P018 人間を不合理のかたまり(限定合理的)としてとらえた上で、現実の経済活動においてどのようにふるまうかを観察、分析する学問が行動経済学です。行動経済学では、「人の嗜好や好みは状況や雰囲気に応じて、その都度変化する」と考えます。 合理的ではない例です。 「選択肢が多いほど効用を最大化できる」とするのが伝統的経済学です。ですが実際には、「選択肢が多すぎると、混乱する」のです。選択麻痺という状態です。 ジャムの試食が、6種類の場合と、24種類の場合の実験です。当然後者の方が「選択肢が多い」のですが、売れたのは前者の6種類の方でした。人間は選択肢が多すぎるとかえって選択そのものをあきらめてしまうのです。これは「ジャムの法則」といいます。 「松」「竹」「梅」のすしセットがあります。 加えて「ホタテ盛り」「日替わり限定セット」「マグロ尽くし」「海鮮丼」「ちらし・・」と増えれば増えるほど、「分からなく」なってきます。 「無数が参加する市場」など、そもそも幻想なのです。 …経済学が発展するにつれて方法論のレパートリーと証拠の情報源が拡大し、経済学という科学はさらに強大となり、いかさま師は暴かれることになるだろう。 そうですね。「科学」は細分化しますから、「普遍妥当性」ではなく、局所的に妥当する「科学的経済学」は、強大(ますますさかん)になるでしょうね。「この理論が完璧で、普遍妥当性がある=いつでもどこでも成り立つ」などという「いかさま経済学師」は排除されるでしょう。 でも、そこまでです。「科学」というものの限界です。 経済学は、最低でも、2つ以上の視点が必要です。 「需要」と「供給」 「生産者」と「消費者」 「価格」と「量」 「短期」と「長期」 「経常黒字」と「資本赤字」 「金融資産」と「金融負債」 国債は「国民資産」と「政府の負債」 「実物経済」と「貨幣経済」 そして、永遠の課題である、 「経済的自由」と「経済的平等」・・・・ この「2つ以上の視点」という原理原則を外すと、トンでも論になります。 ありましたよね、「不況になると、生産者は価格を下げて対応する、だからデフレになる」・・・。生産調整という「量」の視点が欠けています。 デフレは「供給に需要が追いつかないデフレギャップに原因がある(実物経済)」、「日銀による金融政策に原因がある(貨幣経済)」、どちらかに偏っているのは、「いかさま経済学師」です。 こんなもの、100年も前に、ワルラスの「一般均衡」理論で、論証済みです。どちらか一方なんて、あり得ません。 「金融緩和をすると、国際暴落で、ハイパーインフレになる」→アホです。「資産」面が見えていません。 「貿易赤字は官民挙げて取り組まなければいけない課題だ」→勘弁してください。 「消費税の軽減税率は、弱者救済のために必要だ、欧州では常識だ」→詭弁です。 これからも、「一面的」な見方で、国民を惑わす、「いかさま経済学師」はなくなりそうもありません。「科学的経済学者」さん、よろしくお願いします。 ちなみに、「自由」と「平等」は、政治の世界では、次のように論じられます。ただし、判断基準にはなりますが、絶対基準ではありません。 ジョン・ロールズの2つの正義原理 第1原理 政治的自由、言論の自由、思想的自由などの基本的な自由の権利は、すべての人へ平等に分配されること 第2原理 以下の2つの条件を満たす不平等は正義にかなう。公正な機会均等のもとで、正当な競争により生じた不平等であること、そのうえで、社会で最も恵まれない人々にとって最大限の利益になる場合であること。 負けた人の再チャレンジが常に可能なことですね。 一方、批判もあります。 アマルティア・セン 第1に、単なる資源配分の平等性だけでなく、人々が多様な資源を活用して生活の質を高め、一定程度の望ましい生を平等に確保できること、言いかえれば、人間が現実に受ける権利の平等を保障するものでなければならない。 第2に、人間が自らの生の質を高め、福利を実現するための能力、すなわち潜在能力の平等化を目指すべき もう、「べき論(価値判断=正しいか正しくないか、善か悪か、美か醜か、美味か不味いか)」の世界に入り込んでいるので、永遠に答は出ません。 あれ、そういえば、 …経済学の問題の一つは、どうしても基本原理の発見よりも政策に焦点を合わせるということだ。…経済政策に焦点を合わせると、科学でないことが多くかかわってくることだ。政治が関与し始め、政治的なジェスチャーが人々の注目という見返りを受ける。ですね。最初から、「べき論」の世界にさらされるという「大前提」があるので、「経済学」って、可哀想です。 Y=C+G+I+EX-IM Gなんて、「べき論」どっぷりの世界です。農業を守るべきか、漁業を守るべきか、図書館でただの本を貸すべきか・・・G予算など、「価値観調整」の結果そのものです。 供給するのは、「財・サービス」ですが、「財」を英語で言うと「goods=善きもの」です。もう、最初から「価値観」の世界にどっぷりと浸っています。ちなみに、「good」は、当然ですが、「The God」から来ています。 自由を追求すると、「古典派経済学」、平等を追求すると、「共産主義」です。折衷案で、「修正資本主義」があります。 生産者であり、消費者である・・・会社を一歩出ると、コンビニで買い物する消費者。ウーン、見事な「2元統一」です。 哲学の世界では、「生産者(正)-消費者(反)→実在(合)」・・・マルクスですね。あるいは、「絶対矛盾の自己統一(西田幾多郎)」ですね。 人間なんて、そもそも、矛盾のかたまりです。でも平然と「存在」し続けています。不思議です。 人間とは何か・・・古代からの永遠の課題です。これを解明しようとして、科学(細分化)が発展してきました。 と、結論は、 松尾 匡 『対話でわかる 痛快明解 経済学史』 日経BP社 と、正反対になってしまいました(笑)。 松尾先生は、メタ理論(一つの理論で、全てを説明する)はあるといいます。相対的経済学の時代は終わるといいます。 ですが・・・現実は・・・ 経常赤字で財政黒字国(チリ)、経常赤字で財政赤字国(米英)、経常黒字で財政赤字国(日中)、経常黒字で財政黒字国(UAE)。 基軸通貨国(米)と、資本非自由化国(中)・・・ マリファナ製造販売を合法化したウクライナと、大麻禁止の日本、吸うのは自由なオランダ・・・ 豚肉を禁止されるイスラム教徒、牛を禁忌し、高カーストほど菜食主義なインド・・・ 飲酒が原則禁止されるイスラム教国、なければ実験用アルコールにまで手を出したロシア。 売春が合法化される欧米、姦淫(特に女性)が石打の刑で殺害される中東イスラム、女性性器切除が行われるアフリカ。 24時間休まないコンビニ国日本、日曜日に商店は全休するキリスト教国ドイツ。 医者もパイロットも薄給公務員だが、医療も大学も介護も無料のキューバと、体制維持のため、見せしめ処刑する北朝鮮。 銃の所持(防衛)を、自由権とし、その自由権を守るために憲法をつくったアメリカ、刀狩以来、庶民が武器を持たない日本。 利子を教義で禁じる(原理に忠実であればあるほど)イスラム教徒は、すでにキリスト教徒よりも多くなっています。増える一方です。世界の1/3以上が、教義上「利子」を禁止している世界で、「利子は結果(新古典派)」だの、「利子は手段(ケインジアン)」だの、文字通り、「空理空論」です。 これを、経済学で、分析する? それも、一つの経済理論で説明する? これらのばらばらな現実を、一つの理論で、説明できる・・・やはり、無理です(笑)。
おなじみの、中学校の教科書にさえ掲載されている、経済学の基礎の基礎、「供給・需要」曲線が成立するには、箱庭のような条件が必要です。 (1)財・サービスの内容について完全に知っている、無数の消費者 (2)財・サービスの内容について完全に知っている、無数の生産者 (3)完全競争市場であること(寡占・独占やカルテルを結ばない) (4)消費者は、効用を最大限にするように行動する (5)生産者は利益を最大限にするように行動する ミクロ経済学を基礎にしたマクロ経済学は、この前提を継承します。 池田和人「連続講義・デフレと経済政策―アベノミクスの経済分析」 ・・・1982年、キッドランドとプレスコットが・・・これまで述べてきたような要素を持ったマクロ経済学モデル・・・を示しました。・・・動学的で確率論なモデルです。・・・各時点ですべての市場で需要と供給が一致(均衡)が達成されていると想定され・・・動学的(dynamic)で確率論的(stochastic)な一般均衡(general equilibrium)モデル・・・DSGEと呼ばれるモデル群の先駆けです。 ところが、行動経済学では、ヒトは不合理ではないか?を前提とします。 山岡 道男, 浅野 忠克「ガブッ!とわかる世界一やさしい行動経済学の教室」 P018 人間を不合理のかたまり(限定合理的)としてとらえた上で、現実の経済活動においてどのようにふるまうかを観察、分析する学問が行動経済学です。行動経済学では、「人の嗜好や好みは状況や雰囲気に応じて、その都度変化する」と考えます。 合理的ではない例です。 「選択肢が多いほど効用を最大化できる」とするのが伝統的経済学です。ですが実際には、「選択肢が多すぎると、混乱する」のです。選択麻痺という状態です。 ジャムの試食が、6種類の場合と、24種類の場合の実験です。当然後者の方が「選択肢が多い」のですが、売れたのは前者の6種類の方でした。人間は選択肢が多すぎるとかえって選択そのものをあきらめてしまうのです。これは「ジャムの法則」といいます。 「松」「竹」「梅」のすしセットがあります。 加えて「ホタテ盛り」「日替わり限定セット」「マグロ尽くし」「海鮮丼」「ちらし・・」と増えれば増えるほど、「分からなく」なってきます。 「無数が参加する市場」など、そもそも幻想なのです。 …経済学が発展するにつれて方法論のレパートリーと証拠の情報源が拡大し、経済学という科学はさらに強大となり、いかさま師は暴かれることになるだろう。 そうですね。「科学」は細分化しますから、「普遍妥当性」ではなく、局所的に妥当する「科学的経済学」は、強大(ますますさかん)になるでしょうね。「この理論が完璧で、普遍妥当性がある=いつでもどこでも成り立つ」などという「いかさま経済学師」は排除されるでしょう。 でも、そこまでです。「科学」というものの限界です。 経済学は、最低でも、2つ以上の視点が必要です。 「需要」と「供給」 「生産者」と「消費者」 「価格」と「量」 「短期」と「長期」 「経常黒字」と「資本赤字」 「金融資産」と「金融負債」 国債は「国民資産」と「政府の負債」 「実物経済」と「貨幣経済」 そして、永遠の課題である、 「経済的自由」と「経済的平等」・・・・ この「2つ以上の視点」という原理原則を外すと、トンでも論になります。 ありましたよね、「不況になると、生産者は価格を下げて対応する、だからデフレになる」・・・。生産調整という「量」の視点が欠けています。 デフレは「供給に需要が追いつかないデフレギャップに原因がある(実物経済)」、「日銀による金融政策に原因がある(貨幣経済)」、どちらかに偏っているのは、「いかさま経済学師」です。 こんなもの、100年も前に、ワルラスの「一般均衡」理論で、論証済みです。どちらか一方なんて、あり得ません。 「金融緩和をすると、国際暴落で、ハイパーインフレになる」→アホです。「資産」面が見えていません。 「貿易赤字は官民挙げて取り組まなければいけない課題だ」→勘弁してください。 「消費税の軽減税率は、弱者救済のために必要だ、欧州では常識だ」→詭弁です。 これからも、「一面的」な見方で、国民を惑わす、「いかさま経済学師」はなくなりそうもありません。「科学的経済学者」さん、よろしくお願いします。 ちなみに、「自由」と「平等」は、政治の世界では、次のように論じられます。ただし、判断基準にはなりますが、絶対基準ではありません。 ジョン・ロールズの2つの正義原理 第1原理 政治的自由、言論の自由、思想的自由などの基本的な自由の権利は、すべての人へ平等に分配されること 第2原理 以下の2つの条件を満たす不平等は正義にかなう。公正な機会均等のもとで、正当な競争により生じた不平等であること、そのうえで、社会で最も恵まれない人々にとって最大限の利益になる場合であること。 負けた人の再チャレンジが常に可能なことですね。 一方、批判もあります。 アマルティア・セン 第1に、単なる資源配分の平等性だけでなく、人々が多様な資源を活用して生活の質を高め、一定程度の望ましい生を平等に確保できること、言いかえれば、人間が現実に受ける権利の平等を保障するものでなければならない。 第2に、人間が自らの生の質を高め、福利を実現するための能力、すなわち潜在能力の平等化を目指すべき もう、「べき論(価値判断=正しいか正しくないか、善か悪か、美か醜か、美味か不味いか)」の世界に入り込んでいるので、永遠に答は出ません。 あれ、そういえば、 …経済学の問題の一つは、どうしても基本原理の発見よりも政策に焦点を合わせるということだ。…経済政策に焦点を合わせると、科学でないことが多くかかわってくることだ。政治が関与し始め、政治的なジェスチャーが人々の注目という見返りを受ける。ですね。最初から、「べき論」の世界にさらされるという「大前提」があるので、「経済学」って、可哀想です。 Y=C+G+I+EX-IM Gなんて、「べき論」どっぷりの世界です。農業を守るべきか、漁業を守るべきか、図書館でただの本を貸すべきか・・・G予算など、「価値観調整」の結果そのものです。 供給するのは、「財・サービス」ですが、「財」を英語で言うと「goods=善きもの」です。もう、最初から「価値観」の世界にどっぷりと浸っています。ちなみに、「good」は、当然ですが、「The God」から来ています。 自由を追求すると、「古典派経済学」、平等を追求すると、「共産主義」です。折衷案で、「修正資本主義」があります。 生産者であり、消費者である・・・会社を一歩出ると、コンビニで買い物する消費者。ウーン、見事な「2元統一」です。 哲学の世界では、「生産者(正)-消費者(反)→実在(合)」・・・マルクスですね。あるいは、「絶対矛盾の自己統一(西田幾多郎)」ですね。 人間なんて、そもそも、矛盾のかたまりです。でも平然と「存在」し続けています。不思議です。 人間とは何か・・・古代からの永遠の課題です。これを解明しようとして、科学(細分化)が発展してきました。 と、結論は、 松尾 匡 『対話でわかる 痛快明解 経済学史』 日経BP社 と、正反対になってしまいました(笑)。 松尾先生は、メタ理論(一つの理論で、全てを説明する)はあるといいます。相対的経済学の時代は終わるといいます。 ですが・・・現実は・・・ 経常赤字で財政黒字国(チリ)、経常赤字で財政赤字国(米英)、経常黒字で財政赤字国(日中)、経常黒字で財政黒字国(UAE)。 基軸通貨国(米)と、資本非自由化国(中)・・・ マリファナ製造販売を合法化したウクライナと、大麻禁止の日本、吸うのは自由なオランダ・・・ 豚肉を禁止されるイスラム教徒、牛を禁忌し、高カーストほど菜食主義なインド・・・ 飲酒が原則禁止されるイスラム教国、なければ実験用アルコールにまで手を出したロシア。 売春が合法化される欧米、姦淫(特に女性)が石打の刑で殺害される中東イスラム、女性性器切除が行われるアフリカ。 24時間休まないコンビニ国日本、日曜日に商店は全休するキリスト教国ドイツ。 医者もパイロットも薄給公務員だが、医療も大学も介護も無料のキューバと、体制維持のため、見せしめ処刑する北朝鮮。 銃の所持(防衛)を、自由権とし、その自由権を守るために憲法をつくったアメリカ、刀狩以来、庶民が武器を持たない日本。 利子を教義で禁じる(原理に忠実であればあるほど)イスラム教徒は、すでにキリスト教徒よりも多くなっています。増える一方です。世界の1/3以上が、教義上「利子」を禁止している世界で、「利子は結果(新古典派)」だの、「利子は手段(ケインジアン)」だの、文字通り、「空理空論」です。 これを、経済学で、分析する? それも、一つの経済理論で説明する? これらのばらばらな現実を、一つの理論で、説明できる・・・やはり、無理です(笑)。
_____
追記:
以下の初版2000は章が少ない。
本文へのリンクは切れている。
Recursive Macroeconomic Theory
http://web.stanford.edu/~sargent/ljungqvist.htmlRecursive Macroeconomic Theory
by Lars Ljungqvist (Stockholm School of Economics)
and Thomas J. Sargent (Hoover Institution and Stanford University)
Final April 28 draft. This book is virtually complete and to be published by MIT Press in Fall 2000. It will be withdrawn from this web page in about three weeks. The subject is recursive methods and their applications in macroeconomics and monetary economics. Some chapters are more tentative than others. You can e-mail us at sargent@leland.stanford.edu (sargent).
- Title page greentit.ps
- Preface redintr.ps
- Table of Contents contentsfinal.ps
- Part 1 part1.ps (pages 1-100)
- Part 2 part2.ps (pages 101-200)
- Part 3 part3.ps (pages 201-300)
- Part 4 part4.ps (pages 301-400)
- Part 5 part5.ps (pages 401-end)
- Author Index glossaryfinal.ps
- Subject ndex indexfinal.ps
- Matlab programs index progindexfinal.ps
- References redref.ps
- Time Series red1.ps
- Dynamic Programming red2.ps
- Practical Dynamic Programming red3.ps
- Linear Quadratic Dynamic Programming red4.ps
- Search, Matching and Unemployment red5.ps
- Rational Expectations Equilibrium red6.ps
- Competitive Equilibrium red7.ps
- Overlapping Generations red8.ps
- Ricardian Equivalence red9.ps
- Asset Pricing red10.ps
- Growth red11.ps
- Optimal Taxation with Commitment red12.ps
- Self-Insurance red13.ps
- Incomplete Markets Models red14.ps
- Insurance with Recursive Contracts red15.ps
- Credible Government Policies red16.ps
- Fiscal-Monetary Theories of Inflation red17.ps
- Credit and Currency red18.ps
- Equilibrium Search and Matching red19.ps
- Appendix on Functional Analysis blue15.ps
- Appendix on Dual Filtering and Control blue16.ps
Exercises in Recursive Macroeconomic Theory (Adobe PDF)初版用演習
マドリックは世界を破綻…でサージェントも批判している
#7
13 ルーカスの合理的期待形成仮説が予測を誤ったことについては、次のウェブサイトのまとめを参照。http://www.huppi.com/kangaroo/L-chilucas.htm.
ルーカスらとともに合理的期待形成仮説を確立したトマス・サージェントも、「実質的な経済生産をほとんど損なうことなく」インフレを抑え込むことは可能だと強く主張していた(14)。
14 Sargent, "Stopping Moderate Inflations." 1981
「民主党員は、市民の生活を改善するために、連邦政府の活動領域を拡大させることを望む傾向があり、共和党員[マンキュー?]はそれよりも、集権化が権力の乱用と説明責任の欠如をもたらすことを恐れる傾向がある」と、マンキューは述べている。
15 Mankiw, "Politics Aside."
サージェントが語る『経済学の12の教訓』2014
http://econ101.jp/ノア・スミス-「サージェントが語る『経済学の12/
Tom Sargent Summarizes Economics - Marginal REVOLUTION
1. 仮に実現されたとしたら望ましいのだが(残念ながら)実現可能ではないという例は数多い。
2. 個人も社会もともにトレードオフに直面している。
3. 誰もが自らの能力や努力、好みについて他人よりも多くの情報を持ち合わせている。
4. 誰もがインセンティブに反応する。あなたが助けの手を差し伸べたいと考えている人たちもその例外ではない。セーフティネットが必ずしも意図した通りの結果をもたらさないのはそのためだ。
5. 平等(公平)と効率の間にはトレードオフが存在する。
6. ゲームの均衡においては(あるいは経済が均衡に落ち着いている状況においては)人々は皆自らの選択に満足している。善意ある第三者がやって来て状況を変えようと試みても(いい方向/悪い方向のどちらであれ)なかなか事態に変化が表れないのはそのためだ。
7. 誰もがインセンティブに反応するのは今(現時点)だけに限られるわけではない。将来においてもまたそうである。約束したいという思いはあってもそうはいかない(約束できない)というケースがあるのはそのためだ。例えば、時間が経って約束を果たさないといけなくなった時にその通りに行動する(約束を守る)ことがその人の得にはならないとしよう。そのことが広く知れ渡っている場合、一体誰がその人の約束を信じるだろうか? このことから次のような教訓が導かれる。約束をする前に一旦立ち止まって次のように自問してみよう。(約束する時に想定していたのとは)状況が変わっても自分はその約束を守り抜く気はあるだろうか?、と。このことを実践していれば名声(reputation)を手にすることができるはずだ。
8. 政府や投票者もインセンティブに反応する。時に政府がデフォルトを宣言したり約束を反故にすることがあるのはそのためだ。
9. 次の世代(将来世代)に費用の負担を押し付けることは可能だ。国債(の発行を通じた財政赤字の埋め合わせ)やアメリカの社会保障制度(シンガポールの社会保障制度は別)などはそのための典型的な方法だと言える。
10. 政府による支出はいずれは国民がその費用を負担することになる。費用を負担するのは今日かもしれないし明日かもしれない。税金の支払いといったはっきりと目につくかたちでの負担となるかもしれないし、インフレーションを通じた目につきにくいかたちでの負担となるかもしれない。どういうかたちであれ、政府が行う支出はいずれは国民がその費用を負担することになるのだ。
11. 大半の人は公共財の供給や移転支出(特に自分が受け取る移転支出)に要する費用を他人に負担させたがるものだ。
12. 市場で成り立っている価格は多くの取引参加者の持つ情報を集約している。だからこそ、株価や金利、為替レートの今後の行方を予測することは困難なのだ。
Tom Sargent Summarizes Economics
1. Many things that are desirable are not feasible.
2. Individuals and communities face trade-offs.
3. Other people have more information about their abilities, their efforts, and their preferences than you do.
4. Everyone responds to incentives, including people you want to help. That is why social safety nets don’t always end up working as intended.
5. There are tradeoffs between equality and efficiency.
6. In an equilibrium of a game or an economy, people are satisfied with their choices. That is why it is difficult for well meaning outsiders to change things for better or worse.
7. In the future, you too will respond to incentives. That is why there are some promises that you’d like to make but can’t. No one will believe those promises because they know that later it will not be in your interest to deliver. The lesson here is this: before you make a promise, think about whether you will want to keep it if and when your circumstances change. This is how you earn a reputation.
8. Governments and voters respond to incentives too. That is why governments sometimes default on loans and other promises that they have made.
9. It is feasible for one generation to shift costs to subsequent ones. That is what national government debts and the U.S. social security system do (but not the social security system of Singapore).
10. When a government spends, its citizens eventually pay, either today or tomorrow, either through explicit taxes or implicit ones like inflation.
11. Most people want other people to pay for public goods and government transfers (especially transfers to themselves).
12. Because market prices aggregate traders’ information, it is difficult to forecast stock prices and interest rates and exchange rates.
トーマス・ジョン・サージェント(Thomas John Sargent、1943年7月19日 - )は、カリフォルニア州パサデナ生まれのアメリカ合衆国の経済学者。ニューヨーク大学バークレー経済学・経営学教授。専門はマクロ経済学、貨幣経済学、計量経済学における時系列分析。
1970年代から1980年代にかけて合理的期待仮説の考え方を導入し、マクロ経済学の革新を主導してきた経済学者の一人として知られる。1987年からはカリフォルニア州スタンフォードにあるフーヴァー研究所の上級フェローを務めている。
1970年代から1980年代にかけて合理的期待仮説の考え方を導入し、マクロ経済学の革新を主導してきた経済学者の一人として知られる。1987年からはカリフォルニア州スタンフォードにあるフーヴァー研究所の上級フェローを務めている。
- いわゆる新しい古典派(ニュー・クラシカル)の第1世代に属する経済学者と一般的には見なされており、ロバート・ルーカス、ニール・ウォーレス、ロバート・バローらと共に合理的期待の考え方を取り入れ新しいマクロ経済学の手法の基礎を築いた。サージェントは典型的な合理的期待均衡を共産主義のモデル[1]と評し、鞍点経路が最適経路であり、またその鞍点経路は安定であって他の経路は排除されるという命題を発展させた。
- またマクロ経済政策についていかなる裁量的な財政・金融政策も効果が無いとする政策無効命題を提示し、従来のマクロ経済学の学説に対して真っ向から挑戦した。この挑戦はマクロ経済学及びマクロ経済政策に関して激しい論争を巻き起こし、その論争の結果サージェントらの提唱した新しいマクロ経済学の手法が受容され定着することとなった。
- また彼は貨幣的な要因に基づく景気循環理論を構築し、後の研究に大きな影響を与えた。
- 近年では主にラース・ハンセンと共にロバスト制御を経済学に応用する研究を行っている。
















52 Comments:
合理的期待とインフレーション
著者名等 トーマス・J.サージェント/著 ≪再検索≫
著者名等 国府田桂一/〔ほか〕訳 ≪再検索≫
出版者 東洋経済新報社
出版年 1988.11
大きさ等 22cm 206p
注記 Rational expectations and inflation./の翻訳
NDC分類 337.9
件名 インフレーション ≪再検索≫
件名 合理的期待 ≪再検索≫
目次 第1章 合理的期待とマクロ経済学の再構築;第2章 レーガノミックスとクレディビリ
ティ;第3章 四大インフレーションの終焉;第4章 緩やかなインフレーションの抑制
―ポアンカレとサッチャーの方法;第5章 ある不愉快なマネタリスト算術;第6章 香
港ドル投機についての考察
内容 各章末:参考文献
Recursive Methods in Economic Dynamics — Nancy L. Stokey, Robert E. Lucas, Jr. | Harvard University Press
http://www.hup.harvard.edu/catalog.php?isbn=9780674750968&content=toc
Recursive Methods in Economic Dynamics
Nancy L. Stokey
Robert E. Lucas, Jr.
With Edward C. Prescott
Add to Cart
Product Details
HARDCOVER
$95.50 • £70.95 • €86.00
ISBN 9780674750968
Publication: October 1989
Short
608 pages
6-1/8 x 9-1/4 inches
27 line illustrations
World
Related Subjects
BUSINESS & ECONOMICS: Economics: General
Share This
Facebook TwitterPinterest Email
About This BookAbout the AuthorsReviewsTable of Contents
Preface
Symbols Used
I. The Recursive Approach
1. Introduction
2. An Overview
2.1 A Deterministic Model of Optimal Growth
2.2 A Stochastic Model of Optimal Growth
2.3 Competitive Equilibrium Growth
2.4 Conclusions and Plans
II. Deterministic Models
3. Mathematical Preliminaries
3.1 Metric Spaces and Normed Vector Spaces
3.2 The Contraction Mapping Theorem
3.3 The Theorem of the Maximum
4. Dynamic Programming under Certainty
4.1 The Principle of Optimality
4.2 Bounded Returns
4.3 Constant Returns to Scale
4.4 Unbounded Returns
4.5 Euler Equations
5. Applications of Dynamic Programming under Certainty
5.1 The One-Sector Model of Optimal Growth
5.2 A “Cake-Eating” Problem
5.3 Optimal Growth with Linear Utility
5.4 Growth with Technical Progress
5.5 A Tree-Cutting Problem
5.6 Learning by Doing
5.7 Human Capital Accumulation
5.8 Growth with Human Capital
5.9 Investment with Convex Costs
5.10 Investment with Constant Returns
5.11 Recursive Preferences
5.12 Theory of the Consumer with Recursive Preferences
5.13 A Pareto Problem with Recursive Preferences
5.14 An (s, S) Inventory Problem
5.15 The Inventory Problem in Continuous Time
5.16 A Seller with Unknown Demand
5.17 A Consumption-Savings Problem
6. Deterministic Dynamics
6.1 One-Dimensional Examples
6.2 Global Stability: Liapounov Functions
6.3 Linear Systems and Linear Approximations
6.4 Euler Equations
6.5 Applications
III. Stochastic Models
7. Measure Theory and Integration
7.1 Measurable Spaces
7.2 Measures
7.3 Measurable Functions
7.4 Integration
7.5 Product Spaces
7.6 The Monotone Class Lemma
7.7 Conditional Expectation
8. Markov Processes
8.1 Transition Functions
8.2 Probability Measures on Spaces of Sequences
8.3 Iterated Integrals
8.4 Transitions Defined by Stochastic Difference Equations
9. Stochastic Dynamic Programming
9.1 The Principle of Optimality
9.2 Bounded Returns
9.3 Constant Returns to Scale
9.4 Unbounded Returns
9.5 Stochastic Euler Equations
9.6 Policy Functions and Transition Functions
10. Applications of Stochastic Dynamic Programming
10.1 The One-Sector Model of Optimal Growth
10.2 Optimal Growth with Two Capital Goods
10.3 Optimal Growth with Many Goods
10.4 Industry Investment under Uncertainty
10.5 Production and Inventory Accumulation
10.6 Asset Prices in an Exchange Economy
10.7 A Model of Search Unemployment
10.8 The Dynamics of the Search Model
10.9 Variations on the Search Model
10.10 A Model of Job Matching
10.11 Job Matching and Unemployment
11. Strong Convergence of Markov Processes
11.1 Markov Chains
11.2 Convergence Concepts for Measures
11.3 Characterizations of Strong Convergence
11.4 Sufficient Conditions
12. Weak Convergence of Markov Processes
12.1 Characterizations of Weak Convergence
12.2 Distribution Functions
12.3 Weak Convergence of Distribution Functions
12.4 Monotone Markov Processes
12.5 Dependence of the Invariant Measure on a Parameter
12.6 A Loose End
13. Applications of Convergence Results for Markov Processes
13.1 A Discrete-Space (s, S) Inventory Problem
13.2 A Continuous-State (s, S) Process
13.3 The One-Sector Model of Optimal Growth
13.4 Industry Investment under Uncertainty
13.5 Equilibrium in a Pure Currency Economy
13.6 A Pure Currency Economy with Linear Utility
13.7 A Pure Credit Economy with Linear Utility
13.8 An Equilibrium Search Economy
14. Laws of Large Numbers
14.1 Definitions and Preliminaries
14.2 A Strong Law for Markov Processes
IV. Competitive Equilibrium
15. Pareto Optima and Competitive Equilibria
15.1 Dual Spaces
15.2 The First and Second Welfare Theorems
15.3 Issues in the Choice of a Commodity Space
15.4 Inner Product Representations of Prices
16. Applications of Equilibrium Theory
16.1 A One-Sector Model of Growth under Certainty
16.2 A Many-Sector Model of Stochastic Growth
16.3 An Economy with Sustained Growth
16.4 Industry Investment under Uncertainty
16.5 Truncation: A Generalization
16.6 A Peculiar Example
16.7 An Economy with Many Consumers
17. Fixed-Point Arguments
17.1 An Overlapping-Generations Model
17.2 An Application of the Contraction Mapping Theorem
17.3 The Brouwer Fixed-Point Theorem
17.4 The Schauder Fixed-Point Theorem
17.5 Fixed Points of Monotone Operators
17.6 Partially Observed Shocks
18. Equilibria in Systems with Distortions
18.1 An Indirect Approach
18.2 A Local Approach Based on First-Order Conditions
18.3 A Global Approach Based on First-Order Conditions
References
Index of Theorems
General Index
RELATED LINKS
View the companion volume, Solutions Manual for Recursive Methods in Economic Dynamics
ルベーグ積分
変数の値がaからbに変化する時における関数fの積分は、図の青く塗られた部分の面積として表される
数学において関数の積分はその関数と x 軸の間の図形の面積とみなすことができる。ルベーグ積分(ルベーグせきぶん、Lebesgue integral)とは、より広い種類の関数が積分できるように拡張したものである。ルベーグ積分においては、被積分関数は連続である必要はなく、至るところ不連続でもよいし、関数値として無限大をとることがあってもよい。さらに、関数の定義域も拡張され、測度空間と呼ばれる空間で定義された関数を被積分関数とすることもできる。
このような積分の拡張が必要となった背景には、フーリエ級数などの関数列の極限として表される関数に対して、積分と極限操作が可換となるかどうかをリーマン積分で考えるために非常に繊細な議論が必要だったということがある。この点について、ルベーグ積分では、関数列の極限が被積分関数として適当かどうかを考える必要がなく、積分と極限操作の交換も簡単な十分条件が分かっている。
ルベーグ積分の名前は、数学者のアンリ・ルベーグ(Henri Lebesgue、1875年 - 1941年)に由来している。
…
直感的な解釈 編集
積分の定義方法の違いを直感的に理解できるように、山の(海抜より上の部分の)体積を計算する例を考えよう。この山の境界ははっきりと定まっているとする(これが積分範囲である)。
リーマン積分による方法
ケーキを切るときのように、山を縦方向に切り分けて細分する。このとき、各パーツの底面は長方形になるようにする。次に、各パーツで最も標高が高いところを調べ、底面の面積とその標高を掛け合わせる。各パーツごとに計算したその値を足したものを、上リーマン和と呼ぶことにする。同様のことを、最も標高が低いところに対して行い、下リーマン和と呼ぶことにする。分割を細かくしていったときに、上・下のリーマン和が同じ値に収束するときに、リーマン積分可能であるといい、その極限値が山の体積になる。
ルベーグ積分による方法
山の等高線を地図にする。等高線にそって地図を裁断して、地図をいくつかのパーツに分解する。各パーツは面積を計算できる平面図形なので(測度が分かっているので)、パーツの面積とそのパーツの最も低い点の標高を掛け合わせる。各パーツのこの値を足したものを「ルベーグ和」と呼ぶことにする。この「ルベーグ和」はルベーグ積分の構成にあった、単関数の積分に相当する。等高線の間隔を半分にしていったときの「ルベーグ和」の極限値が山の体積になる。
LS Ⅲ章には測度論と積分論、マルコフ過程から始まっている。
だけど、測度論なら伊藤清三の方が詳しいということ。
ルベーグ積分に関しては、LSより伊藤清三『ルベーグ積分入門』の方が解説詳しいし良い。
純粋数学に関しては日本語でたくさんいい本がある。
Amazon.co.jp: Recursive Macroeconomic Theory: Lars Ljungqvist, Thomas J. Sargent: 洋書
http://www.amazon.co.jp/gp/product/0262018748/
愛称LS
Amazon.co.jp: Recursive Methods in Economic Dynamics 電子書籍: Nancy L. Stokey, Edward C. Prescott: Kindleストア
http://www.amazon.co.jp/Recursive-Methods-Economic-Dynamics-Stokey-ebook/dp/B00J8CVOHO/
愛称SLP
Recursive Macroeconomic Theory: Lars Ljungqvist, Thomas J. Sargent: 洋書
http://www.amazon.co.jp/gp/product/0262018748/
Recursive Macroeconomic Theory 電子書籍: Lars Ljungqvist, Thomas J. Sargent: Kindleストア
http://www.amazon.co.jp/Recursive-Macroeconomic-Theory-Lars-Ljungqvist-ebook/dp/B00B74ACEW/
愛称LS
Recursive Methods in Economic Dynamics 電子書籍: Nancy L. Stokey, Edward C. Prescott: Kindleストア
http://www.amazon.co.jp/Recursive-Methods-Economic-Dynamics-Stokey-ebook/dp/B00J8CVOHO/
愛称SLP
まぎらわしい
ケインズに先立ち有効需要の概念を定式化した、
カレツキ『資本主義経済の動態理論』(日本経済評論社)
未来の社会を予見した、
ゲゼル『自然的経済秩序』(ぱる出版)
ケインズ『一般理論』もいいがどうしてもこの2冊になる。
(ケインズによる超国家通貨案=バンコールの元ネタはゲゼルのIVAだ。)
西村和雄『まんがDE入門経済学』(日本評論社)もなかなかいい。
超初心者かつ野球ファンには薦める。稚拙な漫画から欲望が現代経済学の基本だということがわかる。
ここら辺↓を読んでも経済学者が合理的な代表的個人を信じている限り、
大したことは出来ないし、やっていないことがわかる。
Recursive Macroeconomic Theory
Lars Ljungqvist , Thomas J. Sargent
http://pages.stern.nyu.edu/~dbackus/Identification/LS%20RMT2ed%2004.pdf
様々なショックは時間が経てば吸収される(長期的には死んでいる)…
ノイマンによる均斉成長の幻想…に惑わされ、
現代経済学はラムゼー成長理論と最適課税論文の周辺をまわり続けている。
(むしろラムゼーによるケインズ確率論批判がより重要になるだろう。)
質問失礼します。外国部学部2年です。現在独学でミクロ(神取2014→ヴァリアン入門)、マクロ(齊藤他→マンキューマクロ経済学)と勉強しました。
この先のテキストを調べたところ、次のテキストがよさそうだと分かり、この矢印の流れで学習していきたいのですが、いかがでしょうか?
ミクロ:ヴァリアン分析→Silberberg&Suen→MWG、マクロ:Romer→Adda&Cooper→DaronAcemoglu→LS
ちなみにミクロは全範囲を広く浅く、マクロは経済成長論をやりたいです。また、そのあと余裕があれば、ファイナンス・計量・金融論もやりたいのですが、いいテキストあれば教えて下さい。
ヴァリアン、silberbergとmwg全部やるのは流石に冗長かな
アセモグルとローマーもどっちか選択でいいような。
むしろ成長論ならバローサライマーチンを含んだ方が
マクロ:
計量経済学を どのの程度やるか?
DSGEをどの程度やるか?
ミクロ:
行動経済学、ゲーム理論をどの程度やるか?
追記なんとニコルソンの出版社のページから1,2,3章を無料でダウンロードすることが できます(情報提供頂いた曲さん、どうもありがとうございました)。 また、旧版のサイト からは、アクセスコードなしで全てのスライドをダウンロードすることができるようです。 2 章 The Mathematics of Optimization Dixit (1990) “Optimization in Economic Theory, 2nd ed.” A complete and modern treatment of optimization techniques. Use relatively advanced analytical methods. Silberberg and Suen (2001) ...
Silberberg and Suen (2001), The Structure of Economics (3rd) - Scribd
www.scribd.com/.../Silberberg-and-Suen-2001-The-Str...
評価(評価: 5)評価:5-2件のレビュー
Adda and Cooper (2003)
Dynamic Economics: Quantitative Methods and Applications
Jerome Adda (著), Russell W. Cooper (著)
ハードカバー: 296ページ
出版社: Mit Pr (2003/09)
言語 英語
ISBN-13: 978-0262012010
ASIN: 0262012014
Introduction To Modern Economic Growth - アマゾン
www.amazon.co.jp/Introduction.../dp/0691132925
Amazon配送商品ならIntroduction To Modern Economic Growthが通常配送無料。 更にAmazonならポイント還元本が多数。Daron Acemoglu作品ほか、お急ぎ便対象 商品は当日お届けも可能。
The Origins of Power, Prosperity and Poverty - アマゾン
www.amazon.co.jp/Why-Nations-Fail.../1846684307
Amazon配送商品ならWhy Nations Fail: The Origins of Power, Prosperity and Povertyが通常配送無料。更にAmazonならポイント還元本が多数。Daron Acemoglu, James A. Robinson作品ほか、お急ぎ便対象商品は当日お届けも可能。
ダロン・アシモグル - Wikipedia
ja.wikipedia.org/wiki/ダロン・アシモグル
この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典が全くありません。存命人物の記事は特に、検証可能性を満たしている必要が あります。(2015年4月); 出典は脚注などを用いて記述と関連付けてください。(2016年 4月); 脚注による出典の参照が不十分です。脚注を追加し ... 系アメリカ人の経済学者。 マサチューセッツ工科大学エリザベス&ジェイムズ・キリアン記念経済学教授を勤めて いる。 ... 民主主義が経済成長にもたらす影響を考察している。 “Income and Democracy” ...
2017年ノーベル経済学賞予想 --- 参考資料 - SlideShare
www.slideshare.net/YosukeYasuda1/2017-80567962
2017年10月8日 ... 2017年度のノーベル経済学賞(正式には「アルフレッド・ノーベル記念経済学 スウェーデン国立銀行賞」)を予想するために作成したスライドです。昨年度のスライドは こちら: https://www.slideshare.net/YosukeYasuda1/2016-66369696 参考ブログ 記事(note)ーノーベル経済…
2016年ノーベル経済学賞予想 --- 参考資料 - SlideShare
www.slideshare.net/YosukeYasuda1/2016-66369696
2016年のノーベル経済学賞(正式には「アルフレッド・ノーベル記念経済学スウェーデン 国立銀行賞」)を予想するために作成したスライド。昨年度のスライドはこちら: http:// www.slideshare.net/YosukeYasuda1/2015-54841309.
若き経済学者のアメリカ 歴史学と経済学と Natural Experiment
theyoungeconomist.blog115.fc2.com/?m&no=265
彼が「クーリエ・ジャポン」で紹介したイスパニョーラ島の分析(ハイチとドミニカの経済 格差)は、本書第4章 "Intra-Island and Inter-Island Comparisons" にて詳説されて いる。もうひとつ興味深いトピックは、第7章 "From Ancien Regime to Capitalism: The Spread of the French Revolution as a Natural Experiment"。本書の共著者 James Robinson が、Daron Acemoglu, Davide Cantoni, Simon Johnson と共にまとめた 研究で、最も計量経済学的に分析された章である。 James Robinson ...
世界的な経済危機の構造的教訓と経済学 - Global COE Hi-Stat - 一橋 ...
gcoe.ier.hit-u.ac.jp>...>Hi-Stat Vox
世界的な経済危機の構造的教訓と経済学. Daron Acemoglu(MIT and CEPR). 世界 経済の危機は、経済学者にとって課題でありまた好機でもある。このコラムでは、経済 学者の中でも特に創造的な論者であるダロン・アシモグル氏が、これまでの経済学では 今回の危機の到来を予見できなかった背景や理由について論じている。また、危機に 対処する政府に向けて経済学者が出すべき処方箋や、将来の危機を回避するために 若い経済学者が取り組むべき課題について考察している。 世界危機は、経済 ...
Daron Acemoglu (2009) Introduction to Modern ... - Ryo Horii 堀井 亮 (Adobe PDF) -htmlで見る
econ.jpn.org/horii/2012syllabus_advmacro.pdf
科目名:上級マクロ経済学 担当者:堀井 亮. 学期:2学期. 1. 授業の目的と概要. 初歩の 理解を目指す学部レベルのマクロ経済学と、実際の経済分析や政策立案に用いられる 大学院. レベルのマクロ経済学では、経済主体の行動を所与の行動方程式に従うと仮定 するか、ミクロ経済学. と同様に目的関数を最大化するように行動すると考えるかという点 で大きな違いがある。また、マク. ロ経済学では異時点間の消費・貯蓄・投資行動に注目 することから、動学的な最適化を理解し、使い. こなせるようになることが、各応用 ...
Daron Acemoglu: Introduction to Modern Economic Growthーその3 ...
g5arastradero.cocolog-nifty.com/blog/.../daron-acemoglu-.ht...
その1、その2の続きで、まだしつっこく読んでいて、ついに読み終えたのだ! 最後の章 、理論経済学で使われる、ということはこの本でめったやたら使われた数学の基礎事項 のまとめのところはパス! その2で経済成長には「制度」が大切だ、と言っていると書き ましたけれど、Acemogluさんはまじめな学者なので、じゃあ、それぞれの国でそれぞれ の政治制度が実現するのはなぜなのか、も理論的に説明、理解したい。例えば封建 領主である貴族と小作人で作られていたヨーロッパが、なぜ18世紀から ...
Introduction to Modern Economic Growth Kindle版
Daron Acemoglu (著) 2008
https://www.amazon.co.jp/dp/B005DI9R6M/
As long as a branch of science offers an abundance of problems, so long is it alive. —David Hilbert, Paris, 1900
定番:
形式: ハードカバー|Amazonで購入
欧米の大学院でマクロ経済学や経済成長論の定番の教科書。ソローモデルに始まり、新古典派経済成長論、OLGモデル、内生的成長論、方向付き技術変化モデル、技術拡散モデル、そして政治制度モデルなどが扱われる。最初の部では経済成長論を学ぶモチベーション(と基本モデル)が語られ、次の部ではテクニカルな話になり、その次からは本格的に成長論の各種トピックを扱うという構成になっている。飽きずに無理なく読めるだろう。
新古典派経済成長論に向けての準備としてダイナミックプログラミングや制御工学についての章がそれぞれあてられていて、数学的補論が充実している。章末問題もやたら多く、これほど包括的で丁寧な本は類を見ない。政治制度や地理的要因など、他の教科書がしばしば省きがちなトピックに関しても取り上げている。
とにかく経済成長論としては一番オススメです!
神書:
評判がいいので購入してみてPart2のみだいたい読みましたが神書ですw
Part'2は代表的個人からなる動学的一般均衡モデルの基本設定と
離散、連続の非確率的なダイナミックプログラミングを
変分法、最適制御を交えて解説してあります。
まあLucasの前半を簡略化して連続時間をくっつけた感じです。
数学的な予備知識としては邦書の浦井憲か岡田章の経済数学を
講義などでかじったことがあり、そこに書いてある微積分、
微分方程式、位相、凸解析の知識をなんとなく把握していて、
追加で多価写像がなんなのかくらい知っていれば読めると思います。
マクロ経済学の上級の教科書というのはローマーにせよサージェントのrecusiveにせよ、
モデルの根本的な、ある種暗黙の前提や、数学的な処理などで、
「当然お前ら俺らの言ってることわかるだろ?」
というくらいにたいした説明もなく話が進んでいって、
要は著者の言ってることを信じて慣れるしかないという
イラっとくる仕様になっているものですが、
この本はくどいくらいに丁寧に説明してくれますw
一般均衡動学に基づくマクロ経済学、経済成長論を真面目に学びたい人は必携だと思います。
春から院に行くのですが、分野は管理会計です。希望のゼミ(専攻)ではありません。
① その中で、Ljungqvist-Sargentを完全に独学でやりたいのですが、LSの前準備、または、補助としてAcemogluとSundaramで十分ですか?
② また、それ以前の準備として、(主流マクロ)D・ローマー上級、(経済数学)チャン動学、(NK・一般均衡モデル)加藤涼で足りてますかね?
③ 学習ロードマップは(マクロ)D・ローマー→Acemoglu→LS、(数学)チャン動学→Sundaram→SLP、(NK)加藤→Woodford or Gali or walsh?
こんな感じだと把握しているのですが、勘違いがあれば教えてください。
ぜひご回答お願いします。
https://www.amazon.co.jp/First-Course-Optimization-Theory-ebook/dp/B00AKE1UBE/
A First Course in Optimization Theory Kindle版
Rangarajan K. Sundaram (著)1996
最適化理論の教科書.基本的な理論は,KKTの二次の条件や無限Horizonの動的計画問題も含めて,一通り載っている.証明もきちんと書いてある.きちんと書いてあるが,数学ができる人じゃないと読むのはすごく辛いでしょう.なお,かなり経済学よりなので,具体的なデータを入れた後に実質的に解けるかどうかにはほとんど感知していません.
読む人にもよるのでしょうが,例題や証明や論理の流れがどうも直感的には把握しにくいものになっていると思います.評者の場合は,数式番号が入っておらず,当然ながら読みながらの相互参照を促す説明もほとんどないことにストレスがたまりました.
経済学は基本的には最適化問題につきるので、最適化問題の解き方を学習するにはいい本だと思います。最初にざっと数学的基礎(数列の極限、行列、陰関数定理、凹性、凸性…)をおさらいして、条件なし最適化、等式条件付き、不等式条件付きと進み、最後に動学までやります。ひとつひとつ進んでいくので初学者には分かりやすい構成になっていると思います。
表題のとおりFirst courseなのでそれほど数学的に厳密というわけではなく、解き方は分かったけど…という気になるかもしれません。ただ、最適化は深みにはまるとどうしようもない深淵があるなので経済学をやる分にはこれくらいでいいんじゃないかなあという気もします(KKT条件ひとつをとってもこの本だけでは不十分)。大学院や意欲のある学部生でミクロやマクロの数学付録が意味わからんという人にとっては価値があるかと思います。
基礎的な最適化理論についてひととおり学ぶことができる本。ただ、このレベルの本でTarskiの定理に触れているものは、ちょっと珍しいかもしれない。具体例が豊富で、その定理の仮定がどうして必要なのかということについてきっちり理解できるという点は、初学者には嬉しいところ。誤植や論理の飛びも散見するが、簡単に埋められるレベルである。総じて、良書と言っていいだろう。
ただ、第六章のKuhn-Tucker定理の証明は、陰関数定理の使用法に多少の問題があるように思える。これから読む方にはその点に十分留意して読まれることをお勧めする。
Keynes, John Maynard, 353, 922
Keynes, John Maynard. 1940. How to Pay for the War: A Radical Plan for the Chancellor of the Exchequer. London: Macmillan.
922:
25.8. Legal restrictions
This section adapts ideas of Bryant and Wallace (1984) to the turnpike environment. Bryant and Wallace and Villamil (1988) analyzed situations in which the government could make all savers better oby introducing a price discrimination scheme for marketing its debt. The analysis formalizes some ideas mentioned by John Maynard Keynes (1940).
Figure 25.8.1 depicts the terms on which an odd agent at t = 0 can transfer consumption between 0 and 1 in an equilibrium with inationary nance. The agent is endowed at the point (1;0). The monetary mechanism allows him to transfer consumption between periods on the terms c1 = R(1c0), depicted by the budget line connecting 1 on the ct-axis with the point B on the ct+1-axis. The government insists on raising revenues in the amount g for each pair of an odd and an even agent, which means that R must be set so that the tangency between the agent's indierence curve and the budget line c1 = R(1c0
354:
21 For more about this method, see Den Haan and Marcet (1994) and Judd (1998). 22 Calculating Euler equation errors, but for a dierent purpose, goes back a long time. In chapter 2 of The General Theory of Interest, Prices, and Money, John Maynard Keynes noted that plugging in data (not a candidate simulation) into (11:8:2) would produce big residuals. Keynes therefore proposed to replace classical labor supply theory with the assumption that nominal wages are e
ケインズ、ジョン・メイナード、353、922
ケインズ、ジョン・メイナード。戦争のための支払い方法:国庫長官のための根本的な計画。ロンドン:Macmillan。
922:
25.8。法的規制
このセクションでは、ブライアントとウォレス(1984)のアイデアをターンパイケ環境に適応させる。 Bryant and Wallace and Villamil(1988)は、政府がすべての貯蓄者に借金をマーケティングするための価格差別制度を導入することをより良くすることができる状況を分析した。この分析では、ジョン・メイナード・ケインズ(John Maynard Keynes、1940)が述べたいくつかの考えを公式化する。
図25.8.1に、t = 0の奇数エージェントが、インネシアナル・ナンスとの均衡で0と1の間で消費を移すことができるという用語を示します。エージェントはポイント(1; 0)に与えられる。通貨メカニズムは、ct軸上の1とct + 1軸上のB点を結ぶ予算線で表される期間c1 = R(1c0)の期間に消費を移転させることができます。政府は、奇数と偶数のエージェントのそれぞれの対についての収益gを上げることを主張している。つまり、エージェントのインジエンス曲線と予算線c1 = Rの間の接線(1c0
354:
この方法の詳細については、Den Haan and Marcet(1994)とJudd(1998)を参照。オイラー方程式の誤差を計算することは、別の目的のためには、長い時間がかかります。 John Maynard Keynesは、興味のある一般理論、第2章では、(候補シミュレーションではなく)データを(11:8:2)に差し込むと大きな残差が生じることに留意した。したがって、ケインズは古典的労働供給理論を名目賃金が外生的であるという仮定に置き換えることを提案した。
Keynes therefore proposed to replace classical labor supply theory with the assumption that nominal wages are exogenous.
一般理論
#2:2
企業者との貨幣〔賃金〕交渉を改定することによって労働者の全体が実質賃金を所定の水準にまで切り下げることができる、そうした便法は、なんら存在しないかもしれない。これがわれわれの主張である。一般実質賃金水準を決定するのは、第一義には、なにか他の諸力であることを示すようつとめたい。この問題を解明しようとする試みは本書の主題の一つである。
Sargent & Wallace “Some Unpleasant Monetarist Arithmetic Thomas Sargent,Neil Wallace” (1981)
[マネタリストにとっては少々不愉快な算術、ある不愉快なマネタリスト算術]*
https://www.minneapolisfed.org/research/qr/qr531.pdf 全19頁
*
https://www.amazon.co.jp/dp/4492311785/
合理的期待とインフレーション 単行本 – 1988/11
トーマス・J. サージェント (著), 国府田 桂一 (翻訳), 榊原 健一 (翻訳), 鹿野 嘉昭 (翻訳)
2011年ノーベル経済学賞受賞者のトーマス・J・サージェントの論文集です。
収録論文
1.「合理的期待とマクロ経済学の再構築」
2.「レーガノミックスとクレディビリティ」
3.「4大インフレーションの終焉」
4.「緩やかなインフレーションの抑制」
5.「ある不愉快なマネタリスト算術」ウォレスとの共著
6.「香港ドル投機についての考察」ビアーズとウォレスとの共著
ちなみにアセモグルとサージェントとでは立場及び主張が分かれる。
サージェントの主張は以下でわかる
“Some Unpleasant Monetarist Arithmetic” Thomas Sargent,Neil Wallace (1981)*
https://www.minneapolisfed.org/research/qr/qr531.pdf 邦訳あり 全19頁
*
邦訳「ある不愉快なマネタリスト算術」は『合理的期待とインフレーション』1988/11に所収
https://www.amazon.co.jp/dp/4492311785/
サージェントLSはケインズ一般理論#2:2賃金理論に着目する。賃金決定は外生的なのだ。
サージェントと近いのはシムズだ。
Sims, C.A.(1994),“A Simple Model for Study of the Determination of the Price Level and the Interaction of ...
http://web.mit.edu/14.461/www/part1/sims.pdf
(シムズは思想はフリードマン寄りだが現状認識がケインズ寄りになった)
国家を擁護するサージェントに対してアセモグルは国家を衰退する べ き ものとする。
アセモグルの主張は以下でよくわかる。
アセモグル『国家はなぜ衰退するのか──権力・繁栄・貧困の起源』(共著。邦訳・早川書房)。
学者としての代表作とは言えないが主張はわかりやすい。
『世界を破綻させた経済学者たち』(ジェフ・マドリック)にアセモグルへの批判がある。
厳密にはフリードマンへの批判だが。
《大ざっぱにいえば、豊かになった国々は、自由放任主義の市場をうまく機能させるのに
適した制度を築いていたと、アセモグルとロビンソンは主張する。…
[共著『国家はなぜ衰退するのか──権力・繁栄・貧困の起源』(邦訳・早川書房)2013]…
具体的には、私有財産と契約の保護が確立されていること、効率的な金融システムが存在
すること、事業の開業に対する規制が最低限にとどまっいることなどが必要だという。…
アセモグルとロビンソンは、経済発展を遂げている社会が擁している制度の例を挙げる際に、
自由市場を保護・促進するような制度ばかりに光を当てる傾向がある。また、ある種の制度が
経済発展を生むのか、経済発展がある種の制度を生むのかという因果関係も十分に立証でき
ていない。因果関係の連鎖の始まりがなんだったのかが明らかでないのだ。》
ちなみにアセモグルとサージェントとでは立場及び主張が分かれる。
サージェントの主張は以下でわかる
“Some Unpleasant Monetarist Arithmetic” Thomas Sargent,Neil Wallace (1981)*
https://www.minneapolisfed.org/research/qr/qr531.pdf 邦訳あり 全19頁
*
邦訳「ある不愉快なマネタリスト算術」は『合理的期待とインフレーション』1988/11に所収
https://www.amazon.co.jp/dp/4492311785/
サージェントLSはケインズ一般理論#2:2賃金理論に着目する。賃金決定は外生的なのだ。
サージェントと近いのはシムズだ。
Sims, C.A.(1994),“A Simple Model for Study of the Determination of the Price Level and the Interaction of ...
http://web.mit.edu/14.461/www/part1/sims.pdf
(シムズは思想はフリードマン寄りだったが現状認識がケインズ寄りになった)
国家を擁護するサージェントに対してアセモグルは国家を衰退する べ き ものとする。
アセモグルの主張は以下でよくわかる。
アセモグル『国家はなぜ衰退するのか──権力・繁栄・貧困の起源』(共著。邦訳・早川書房)。
学者としての代表作とは言えないが主張はわかりやすい。
『世界を破綻させた経済学者たち』(ジェフ・マドリック)にアセモグルへの批判がある。
厳密にはフリードマンへの批判だが。
《大ざっぱにいえば、豊かになった国々は、自由放任主義の市場をうまく機能させるのに
適した制度を築いていたと、アセモグルとロビンソンは主張する。…
[共著『国家はなぜ衰退するのか──権力・繁栄・貧困の起源』(邦訳・早川書房)2013]…
具体的には、私有財産と契約の保護が確立されていること、効率的な金融システムが存在
すること、事業の開業に対する規制が最低限にとどまっいることなどが必要だという。…
アセモグルとロビンソンは、経済発展を遂げている社会が擁している制度の例を挙げる際に、
自由市場を保護・促進するような制度ばかりに光を当てる傾向がある。また、ある種の制度が
経済発展を生むのか、経済発展がある種の制度を生むのかという因果関係も十分に立証でき
ていない。因果関係の連鎖の始まりがなんだったのかが明らかでないのだ。》
ちなみにアセモグルとサージェントとでは立場及び主張が分かれる。
サージェントの主張は以下でわかる
“Some Unpleasant Monetarist Arithmetic” Thomas Sargent,Neil Wallace (1981)*
https://www.minneapolisfed.org/research/qr/qr531.pdf 邦訳あり 全19頁
*
邦訳「ある不愉快なマネタリスト算術」は『合理的期待とインフレーション』1988/11に所収
https://www.amazon.co.jp/dp/4492311785/
サージェントLSはケインズ一般理論#2:2賃金理論に着目する。賃金決定は外生的なのだ。
サージェントと近いのはシムズだ。
Sims, C.A.(1994),“A Simple Model for Study of the Determination of the Price Level and the Interaction of ...
http://web.mit.edu/14.461/www/part1/sims.pdf
(シムズは思想はフリードマン寄りだったが現状認識がケインズ寄りになった)
国家を擁護するサージェントに対してアセモグルは国家を衰退する べ き ものとする。
アセモグルの主張は以下でよくわかる。
アセモグル『国家はなぜ衰退するのか──権力・繁栄・貧困の起源』(共著。邦訳・早川書房)。
学者としての代表作とは言えないが主張はわかりやすい。
『世界を破綻させた経済学者たち』(ジェフ・マドリック)にアセモグルへの批判がある。
厳密にはフリードマンへの批判だが。
《大ざっぱにいえば、豊かになった国々は、自由放任主義の市場をうまく機能させるのに
適した制度を築いていたと、アセモグルとロビンソンは主張する。…
具体的には、私有財産と契約の保護が確立されていること、効率的な金融システムが存在
すること、事業の開業に対する規制が最低限にとどまっいることなどが必要だという。…
アセモグルとロビンソンは、経済発展を遂げている社会が擁している制度の例を挙げる際に、
自由市場を保護・促進するような制度ばかりに光を当てる傾向がある。また、ある種の制度が
経済発展を生むのか、経済発展がある種の制度を生むのかという因果関係も十分に立証でき
ていない。因果関係の連鎖の始まりがなんだったのかが明らかでないのだ。》
マドリックはサージェントも批判している
#7
13 ルーカスの合理的期待形成仮説が予測を誤ったことについては、次のウェブサイトのまとめを参照。http://www.huppi.com/kangaroo/L-chilucas.htm.
https://translate.google.com/translate?sl=en&tl=ja&u=http%3A//www.huppi.com/kangaroo/L-chilucas.htm
ルーカスらとともに合理的期待形成仮説を確立したトマス・サージェントも、「実質的な経済生産をほとんど損なうことなく」インフレを抑え込むことは可能だと強く主張していた(14)。
14 Sargent, "Stopping Moderate Inflations."
「民主党員は、市民の生活を改善するために、連邦政府の活動領域を拡大させることを望む傾向があり、共和党員[マンキュー?]はそれよりも、集権化が権力の乱用と説明責任の欠如をもたらすことを恐れる傾向がある」と、マンキューは述べている。
15 Mankiw, "Politics Aside."
サージェントが語る『経済学の12の教訓』
http://nam-students.blogspot.jp/2018/03/12.html
http://econ101.jp/ノア・スミス-「サージェントが語る『経済学の12/
Tom Sargent Summarizes Economics - Marginal REVOLUTION
http://marginalrevolution.com/marginalrevolution/2014/04/tom-sargent-summarizes-economics.html
1. 仮に実現されたとしたら望ましいのだが(残念ながら)実現可能ではないという例は数多い。
2. 個人も社会もともにトレードオフに直面している。
3. 誰もが自らの能力や努力、好みについて他人よりも多くの情報を持ち合わせている。
4. 誰もがインセンティブに反応する。あなたが助けの手を差し伸べたいと考えている人たちもその例外ではない。セーフティネットが必ずしも意図した通りの結果をもたらさないのはそのためだ。
5. 平等(公平)と効率の間にはトレードオフが存在する。
6. ゲームの均衡においては(あるいは経済が均衡に落ち着いている状況においては)人々は皆自らの選択に満足している。…
7. 誰もがインセンティブに反応するのは今(現時点)だけに限られるわけではない。将来においてもまたそうである。…
8. 政府や投票者もインセンティブに反応する。時に政府がデフォルトを宣言したり約束を反故にすることがあるのはそのためだ。
9. 次の世代(将来世代)に費用の負担を押し付けることは可能だ。…
10. 政府による支出はいずれは国民がその費用を負担することになる。…
11. 大半の人は公共財の供給や移転支出(特に自分が受け取る移転支出)に要する費用を他人に負担させたがるものだ。
12. 市場で成り立っている価格は多くの取引参加者の持つ情報を集約している。だからこそ、株価や金利、為替レートの今後の行方を予測することは困難なのだ。
1. Many things that are desirable are not feasible.
2. Individuals and communities face trade-offs.
3. Other people have more information about their abilities, their efforts, and their preferences than you do.
4. Everyone responds to incentives, including people you want to help. That is why social safety nets don’t always end up working as intended.
5. There are tradeoffs between equality and efficiency.
6. In an equilibrium of a game or an economy, people are satisfied with their choices. That is why it is difficult for well meaning outsiders to change things for better or worse.
7. In the future, you too will respond to incentives. That is why there are some promises that you’d like to make but can’t. No one will believe those promises because they know that later it will not be in your interest to deliver. The lesson here is this: before you make a promise, think about whether you will want to keep it if and when your circumstances change. This is how you earn a reputation.
8. Governments and voters respond to incentives too. That is why governments sometimes default on loans and other promises that they have made.
9. It is feasible for one generation to shift costs to subsequent ones. That is what national government debts and the U.S. social security system do (but not the social security system of Singapore).
10. When a government spends, its citizens eventually pay, either today or tomorrow, either through explicit taxes or implicit ones like inflation.
11. Most people want other people to pay for public goods and government transfers (especially transfers to themselves).
12. Because market prices aggregate traders’ information, it is difficult to forecast stock prices and interest rates and exchange rates.
164また,本章の議論は実際にはマクロ経済学の政府の予算制約に関する文献にある推論に沿ったものであり,たとえばマッカラム[9,10]やスカース[14]がこの論法で論じていることに留意すべきである。多くの著者が指摘していることであるが,実質利子率が経済成長率よりも大きいときには,政府の予算制約は実質債務についての不安定な差分方程式として表すことができ,そしてこのことは,貨幣成長の「カパーセント」ルールのもとでは1人当り実質政府債務残高の経路が発散的であることを意味している。この章で行ったことは,反インフレTション政策の意味するところ,そしてこのような発散的経路を永久に続けることはできないということ, を単に指摘したにすぎない。本章の結論を得るために二つの重要な仮定を置いた。第一は,実質利子率が経済成長率よりも高い, というものである。これを仮定した理由は,現在の赤字がいかなるものであれ,低い貨幣の成長率に賛成する多くの人々がこの仮定を採用しているように思われるからである。この仮定を別のものに置き換えるとすれば,民間部門の国債需要が実質収益率の増加関数であり,経済成長率よりも小さいかあるいは負の実質収益率のもとではその需要が正である, ということを仮定することであろう。しかし,国債に対する一層大きな需要をll■起するためには実質利子率が経済成長率を上回ると仮定しなければならない。さらに, 1人当り国債需要量には上限がある, と引き続き仮定する.このような国債需要関数を仮定することは,国債の実質利子率が金融政策に影響されること,また国債供給を非常に少なくするような金融政策のもとでは,ベースマネーからだけでなく国債からもシーニョリッジが得られるということを意味する。しかし,このような形で国債需要を織り込んだ分析を行ったとしても,十分に強い金融引締め政策は政府有利子債務の急速な増加を意味するから,金融緩和政策よりも将来のインフレーションを高める結果になるのである。第二番目の重要な仮定は,D(′)の時間的経路が所与であり,現在や将来の金融政策には依存しない, というものである。この仮定は,一番目の仮定のような経済主体の選好,機会,ある,いは行動に関するものではなく,通貨および財政当局の行動に関する仮定であり,彼らが演じている「ゲーム」に関する仮定である。通貨当局は収入源としてシーニョリッジが利用される度合いに影響を与えるため,金融政策と財政政策は協調されねばならないのである。問題はどちらが一一通貨当局か財政当局か――「手番を先にとる」か,言い換えれば
4また,本章の議論は実際にはマクロ経済学の政府の予算制約に関する文献にある推論に沿ったものであり,たとえばマッカラム[9,10]やスカース[14]がこの論法で論じていることに留意すべきである。多くの著者が指摘していることであるが,実質利子率が経済成長率よりも大きいときには,政府の予算制約は実質債務についての不安定な差分方程式として表すことができ,そしてこのことは,貨幣成長の「カパーセント」ルールのもとでは1人当り実質政府債務残高の経路が発散的であることを意味している。この章で行ったことは,反インフレTション政策の意味するところ,そしてこのような発散的経路を永久に続けることはできないということ, を単に指摘したにすぎない。本章の結論を得るために二つの重要な仮定を置いた。第一は,実質利子率が経済成長率よりも高い, というものである。これを仮定した理由は,現在の赤字がいかなるものであれ,低い貨幣の成長率に賛成する多くの人々がこの仮定を採用しているように思われるからである。この仮定を別のものに置き換えるとすれば,民間部門の国債需要が実質収益率の増加関数であり,経済成長率よりも小さいかあるいは負の実質収益率のもとではその需要が正である, ということを仮定することであろう。しかし,国債に対する一層大きな需要をll■起するためには実質利子率が経済成長率を上回ると仮定しなければならない。さらに, 1人当り国債需要量には上限がある, と引き続き仮定する.このような国債需要関数を仮定することは,国債の実質利子率が金融政策に影響されること,また国債供給を非常に少なくするような金融政策のもとでは,ベースマネーからだけでなく国債からもシーニョリッジが得られるということを意味する。しかし,このような形で国債需要を織り込んだ分析を行ったとしても,十分に強い金融引締め政策は政府有利子債務の急速な増加を意味するから,金融緩和政策よりも将来のインフレーションを高める結果になるのである。第二番目の重要な仮定は,D(′)の時間的経路が所与であり,現在や将来の金融政策には依存しない, というものである。この仮定は,一番目の仮定のような経済主体の選好,機会,ある,いは行動に関するものではなく,通貨および財政当局の行動に関する仮定であり,彼らが演じている「ゲーム」に関する仮定である。通貨当局は収入源としてシーニョリッジが利用される度合いに影響を与えるため,金融政策と財政政策は協調されねばならないのである。問題はどちらが一一通貨当局か財政当局か――「手番を先にとる」か,言い換えれば,第5章 ある不愉快なマネタリスト算術 16,どちらがどちらに規律を課すか, ということである。本章で設けられた仮定では財政当局が先に手番をとるが,その手番は'(″)の系列全体から成っている。この系列を所与として,D(′)と整合的になるように金融政策が, もしそれが可能であれば,決定されるのである(すでに述べたように,D(ι)系列が「あまりにも長期」にわたり「あまりにも大きい」場合には不可能となるかもしれない)。政策当局によって演じられるこうしたゲームの仮定を所与とし,さらに第一番目の重要な仮定を所与とすれば,通貨当局が現時点で金融を引き締めれば将来は金融を緩和しなければならなくなるのである。金融的制約の必要性について,この章で行ったのとは別の解釈も可能であり,通貨当局が最初の手番をとり財政当局に規律を課すものとしても解釈できる。この解釈では,通貨当局が最初に,5.4式のようにθを固定するルールを, T期まででなく,すべての′について課すことを宣告する, という形で手番をとることになる。これを拘束性のある仕方で行うことにより,通貨当局は財政当局をして,宣告した金融政策と両立するようなD(′)系列を選択させるのである。この形での永続的な金融的制約は財政的規律を課す上で有効なメカニズムである。以前から提案されている財政的規律を課す上で有効なメカニズムとしては,このほかに,固定為替制度および商品貨幣本位制がある。財政当局に恒久的に規律を課すこのような通貨制度のもとで,金融政策がインフレ率に永続的に影響を与え得る, という可能性を否定するものは,ここでの分析には何もない。この章を執筆したのは,通貨および財政当局によって演じられるゲームに関するわれわれの仮定が金融政策と財政政策が協調されるべき方法を表していると考えたからではなく,これが現在演じられているゲームの方法であるかもしれないと憂慮したからである。この補論では,本文で用いられた仮定が導出できる簡単な理論モデルを述べることにする。モデルはポール・サミュエルソンの世代交代モデルの一つであり,人々は異時点間の消費流列を滑らかにするために貨幣を用いている。経済は′=1の時点から将来に向けて展開されるものとする。経済は2期間
多くの著者が指摘していることであるが,実質利子率が経済成長率よりも大きいときには,政府の予算制約は実質債務についての不安定な差分方程式として表すことができ,そしてこのことは,貨幣成長の「kパーセント」ルールのもとでは1人当り実質政府債務残高の経路が発散的であることを意味している。この章で行ったことは,反インフレーション政策の意味するところ,そしてこのような発散的経路を永久に続けることはできないということ, を単に指摘したにすぎない。
第5章 ある不愉快なマネタリスト算術;
164頁
新フィッシャー主義とFTPL - himaginaryの日記
http://d.hatena.ne.jp/himaginary/20170109/EconReporter_Cochrane_interview
インタビュアー
サージェントはこの理論を30年以上前に開発しましたが、主流派にこれまで採用されてこなかったのはなぜでしょうか? 何が最近変わったのでしょうか?
コクラン
実際のところ、FTPLはもっとずっと以前に遡ります。アダム・スミスは次のような素晴らしい言葉を残しています:
税のうち一定割合はある種の紙幣で支払わなければならない、と布告した王子は、それによってその紙幣に一定の価値を与えているのである。(国富論、第2冊)
“A prince who should enact that a certain proportion of his taxes should be paid in a paper money of a certain kind might thereby give a certain value to this paper money.” (Wealth of Nations, Book II)
ということで、基本的な考えはアダム・スミスにあったのです。
すべての貨幣経済学における謎は、「この紙切れのためになぜ我々はこれほど一生懸命に働くのか?」というものです。考えてみれば、それは本当に謎です。あなたも私も一日中額に汗して働き、家に何を持ち帰るのでしょうか? 死んだ大統領の絵が印刷された幾枚かの紙切れです。この小さな紙切れのためになぜ我々はこれほど一生懸命に働くのでしょうか? 誰かがそれを受け取ると知っているからです。しかしなぜその誰かはそれを受け取るのでしょうか? これが経済学の謎です。
FTPLはこの謎に根本的な回答を与えます。その理由というのは、米国では毎年4月15日に税金を払わなければならないからです。そして納税は、まさにその政府貨幣によって行わねばなりません。かつては羊や山羊で納税していた時代もありましたが、今は受け取ってもらえません。彼らは紙幣を取り戻したがっています。ということで、根本的には、貨幣の価値は、政府がそれを税金として受け取ることから生じているのです。
サージェントの研究はそのことを示す上で極めて素晴らしいものでした。しかしミルトン・フリードマンも、金融政策と財政政策の協調について有名な論文を書いています。ということで、ある意味においては、この理論は昔から存在していたのです。問題は、どの程度重きを置くか、ということに過ぎなかったわけです。
Cochrane, John H. (1998) “A Frictionless View of US Ination.” In Ben S. Bernanke and Julio J. Rotemberg. eds. NBER Macroeconomics Annual 1998. Cambridge, MA US: MIT Press. pp. 323–334.
Sargent & Wallace (1981)
Some Unpleasant Monetarist Arithmetic Thomas Sargent,Neil Wallace (1981)
https://www.minneapolisfed.org/research/qr/qr531.pdf
《ある君主が、かれの税の一定部分は一定の種類の紙幣で支はらわれなければならないという、法令をだすとすれば、かれはそうすることによって、この紙幣に一定の価値をあたえうるであろう。》
アダム・スミス『国富論』2:2最終部
世界の大思想上
参考:
ミルトン・フリードマン 資本主義と自由 Milton Friedman Capitalism and freedom 1962
http://nam-students.blogspot.jp/2015/12/milton-friedman-capitalism-and-freedom.html
「ヘリコプター・マネー」は、米経済学者のミルトン・ フリードマン氏が、1969年の論文(”TheOptimum Quality of Money”)ch.1のなかで提唱された。
1992年MONEY MISCHIEF 『貨幣の悪戯』(1993・三田出版会)2章で再説。
M.フリードマン著『最適通貨量』単著
昭和45年1月 世界経済 161号(p40~p45) 要約のみ
Milton Friedman;The Optimum Quantity of Money And other Essays. 1969.
http://www.asyura2.com/16/hasan117/msg/112.html
Sargent, Thomas J. and Francois R. Velde (1995) “Macroeconomic Features of the French Revolution.” Journal
of Political Economy. Vol. 103. No. 3. pp. 474–518.
Sargent, Thomas J. and Neil Wallace (1981) “Some Unpleasant Monetarist Arithmetic.” Quarterly Review Federal
Reserve Bank of Minneapolis. Vol. 45. pp. 1–17.Fall.
Sargent, Thomas J. (1982) “The Ends of Four Big Inflations.” In Robert E. Hall. ed. Inflation: Causes and Effects.
Chicago, USA: . pp. 41–97.
Sargent, Thomas J. (1987) Macroeconomic Theory. San Diego, CA, USA: Academic Press 2. edition.
Sims, Christopher (1994) “A Simple Model for the Study of the Determination of the Price Level and the Interaction
of Monetary and Fiscal Policy.” Economic Theory. Vol. 4. pp. 381–399.
Sims, Christopher (1999) “Domestic Currency Denominated Government Debt as Equity in the Primary Surplus.”.
齊藤 誠 (@makotosaito0724)
2019/11/03 8:34
通貨史の経済理論的な研究では商品貨幣対国定貨幣という軸はすでに乗り越えられている。Sargent and Velde (2002)をじっくり読めばそれでよい。MMTでクナップやイネスが出てきてなんだか不意打ちを食らうのも、そうした知識が欠落した私達が17世紀末のロックみたく振舞ってしまうからかもしれない。
Twitterアプリをダウンロード
Sargent, T. and Velde, F.: The Big Problem of Small Change ...
press.princeton.edu/titles/7306.html
Thomas J. Sargent & François R. Velde ... Thomas J. Sargent is Donald Lucas Professor of Economics at Stanford ...
Thomas J. Sargent and François R. Velde, The Big Problem of Small ...
www.cambridge.org/.../thomas-j-sargent...francois-r-vel...
Thomas J. Sargent and François R. Velde, The Big Problem of Small Change ( Princeton: Princeton University Press, 2002. 432 pp. $65). - Volume 12 Issue 2 - ISABEL SCHNABEL.
The Big Problem of Small Change by Thomas J. Sargent and ... (Adobe PDF) -htmlで見る
www.cato.org/...2002/big-problem-small-change-thoma...
Thomas J. Sargent and François R. Velde. Princeton: Princeton University Press, 2002, 405 pp. Thomas Sargent of ...
The Big Problem of Small Change (The Princeton Economic History of the Western World Book 51) (English Edition) Kindle版
Thomas J. Sargent (著), François R. Velde (著)
その他(4)の形式およびエディションを表示する
Kindle版
¥5,930
獲得ポイント: 59pt
今すぐお読みいただけます: 無料アプリ
2014
http://hermes-ir.lib.hit-u.ac.jp/rs/bitstream/10086/19997/1/keizaikenkyu05501086.pdf
小額貨幣に関わる重要な問題
残念ながら主流派は時代遅れで効果的な政策を生み出せません
なぜ主流派が国家を嫌うのかはもはや経済学ではなく精神分析の仕事と言わなければなりません
一発逆転を狙うならFTPLとゲゼル減価マネーを融合させることです
金利はそこでは本質的ですから
岩村充の仕事が参考になります
Nice Post...
Can anyone help in HP printer troubleshooting?
While printing, users usually encounter errors or printing issues which require HP printer troubleshooting. Get instant help from the HP customer support team and get your printer issues fixed in a few seconds. The experts identify the root cause of the problem and then help you in rectifying the issue with the best possible solution. They do not use hit and try methods to fix the printer. They have an eye to find the issues immediately and fix them. If you are a pro, try finding the root cause of the issue or simply restart your printer after switching it off and then restart it after 15-20 seconds. This might resolve your issue temporarily.
Nice Post...
Get Help With Office.com/setup | Office Setup Help
Bought a new Office product or thinking to get one? Whatever is the case, you are going to need help with it all. You can buy MS Office from any trusted eCommerce site or the Microsoft website itself. Once, you have the subscription, visit office.com/setup to get started with your product. There you would need to create and sign in to your Office account, enter the Office product key, and then you can download and install the product on your device. After installing the setup, you can activate your Office by signing into your Office account from any Office application. That’s all! Now you can access your Office tool on your computer without any issue. However, if you happen to get any error or any other problem, feel free to visit our Office Setup Help portal for solutions.
Students need to focus on their education instead of getting bogged down in rubbish. I am Monica Jacob and I provide Cheap Dissertation Writing Service to students who want to develop their writing skills.
There may be noticeably a bundle to know about this. I assume you made certain good factors in options also. 메이저사이트
Thanks a bunch for sharing this with all people you actually recognise what you’re speaking approximately! Bookmarked. 온라인경마
Why are you getting tense about tech services? I know the best and reliable service for the RR email which will be a good fit for your requirements. I have also used their service many times and I can tell you that they are amazing with their work. Their service is super fast and user friendly. You must visit their Roadrunner email support website.
Visit their Blog on Roadrunner email problems to get the details.
Dial our Roadrunner email support number to solve all your Roadrunner email problems.
Also, if you want help regarding Microsoft office, then visit our Microsoft Office 365 Support website and get to know in detail.
There are certainly a lot of details like that to take into consideration. That is a great point to bring up. I offer the thoughts above as general inspiration but clearly there are questions like the one you bring up where the most important thing will be working in honest good faith. I don?t know if best practices have emerged around things like that, but I am sure that your job is clearly identified as a fair game. Both boys and girls feel the impact of just a moment?s pleasure, for the rest of their lives.
온라인카지노
wep.
Well I truly enjoyed reading it. This subject offered by you is very helpful and accurate.
토토
Thanks for sharing information with all of us . Who visit your website . good work and great stuff 토토 .
We are one of the leading outlook technical service providers. We will help you to resolve all the errors like “outlook cannot connect to server” and other similar errors. We have been assisting the individual for several years so our facilities are completely safe for purchase. If you still have any questions then you can share that.
Hello, I read the post well. 안전놀이터 It's a really interesting topic and it has helped me a lot. In fact, I also run a website with similar content to your posting. Please visit once
How can you think of this? I thought about this, but I couldn't solve it as well as you.안전놀이터I am so amazing and cool you are. I think you will help me. I hope you can help me.
Hello, I am one of the most impressed people in your article. 온라인바카라 If possible, please visit my website as well. Thank you.
Really appreciate you for sharing your useful thoughts with us, I found it very useful and informative. clu post utme past question
How to Borrow Money from Cash App instantly?
Most often, people have the query about How To Borrow Money from Cash App
. that is usually crucial to handle the cash app account. Different kinds of the methods are needed to sort out the issues of the strategic steps for such purpose. Cash app users need to ask the help of the cash app executives who work with dedication to offer them a consistent help.
Mesotherapy is a technique that uses injections of vitamins, enzymes, hormones and plant extracts to rejuvenate and firm the skin as well as remove excess fat. This technique uses very fine needles to administer a series of injections into the middle layer (mesoderm) skin. The idea behind Mesotherapy in London is that it corrects underlying problems such as poor circulation and inflammation that cause skin damage. The cost of mesotherapy depends on the type of treatment you receive and the number of sessions you need.
Selecting the best stock broker in India depends on your trading preferences, investment goals, and risk tolerance. Each of the brokers mentioned above has its own strengths and weaknesses, so it's essential to evaluate them based on your specific needs. Consider factors such as brokerage charges, trading platforms, research and advisory services, and customer support when making your decision. Ultimately, the best stock broker for you will be the one that aligns with your financial objectives and trading style.
best stock broker
Thanks for sharing an informative blog, IT is an integral part of the business, and every IT project is a business initiative, you have explained everything well, and for the business assignment Business Economics Assignment Help provides for students who face issues receiving outstanding scores in their assignments through helping our experts with their assignments.
コメントを投稿
<< Home