NAMs出版プロジェクト: カレツキ関連追記とヴィクセル的不均衡
http://nam-students.blogspot.jp/2015/09/blog-post_19.html
http://nam-students.blogspot.jp/2015/09/blog-post_19.html
ケインズ=カレツキ往復書簡 Keynes ,Kalecki Correspondence 1937
http://nam-students.blogspot.jp/2015/12/keynes-kalecki-correspondence-1937.html
http://nam-students.blogspot.jp/2015/12/keynes-kalecki-correspondence-1937.html
NAMs出版プロジェクト: ティンバーゲン、シュンペーター、カレツキ
http://nam-students.blogspot.jp/2017/01/blog-post.htmlヒックス『価値と資本』John.Hicks,Value and Capital(1939,1946)
http://nam-students.blogspot.jp/2015/10/johnhicksvalue-and-capital19391946.html
加速度原理
https://kotobank.jp/word/%E5%8A%A0%E9%80%9F%E5%BA%A6%E5%8E%9F%E7%90%86-44848
J・M・クラーク
https://ja.wikipedia.org/wiki/%E3%82%B8%E3%83%A7%E3%83%B3%E3%83%BB%E3%83%A2%E3%8
3%BC%E3%83%AA%E3%82%B9%E3%83%BB%E3%82%AF%E3%83%A9%E3%83%BC%E3%82%AF
https://en.wikipedia.org/wiki/John_Maurice_Clark

https://ja.wikipedia.org/wiki/ロイ・ハロッド
ロイ・ハロッド(Roy Forbes Harrod 、1900年2月13日 - 1978年3月8日)は、イギリスの経済学者。ジョン・メイナード・ケインズの弟子であり、ポスト・ケインジアンの一人。オックスフォード大学で長く教授を務めた。ケインズ経済学の動学化を行い、エブセイ・ドーマーと別々に発表した経済成長論のモデルは、後に「ハロッド・ドーマーモデル」として一般化された。また、国際経済学・不完全競争理論の分野でも業績がある。
研究・人物
ハロッドはケインズ経済学の指導的推進者であり、ケインズの伝記作家でもある。『ケインズ伝』(原書1951年)はケインズの生涯よりも、著作の内容により多く語っているのが特徴である。
ハロッドはケインズの所得決定論を動学化したが、後になって類似の理論をE.ドーマーが発表し「ハロッド=ドーマー・モデル」と呼ばれるようになった。
この他にも、1930年代の不完全競争理論に貢献したり、国際経済論、国際金融論、金融論にも貢献した。
また、経済学以外に『帰納法論理の基礎』(原書1956年)を発表しているが、これはデイヴィッド・ヒュームの「帰納法の問題」を解こうとする重要な業績である。
日本語訳著書
『ハロッド國際經濟學』、藤井茂訳、実業之日本社, 1943年(改訂版1958年、全訂新版1976年)
『動態經濟學序説』、高橋長太郎・鈴木諒一訳、有斐閣、 1953年
『ポンド・スターリング』、東京銀行調査部訳、実業之日本社、1953年
『ケインズ伝』(上巻、下巻)」、塩野谷九十九訳、東洋経済新報社、1954年(改訳版1967年)
『景気循環論―一試論』、宮崎義一・浅野栄一訳、東洋経済新報社、1955年(新版1972年)
:The Trade Cycle, An Essay(1936)
『ドル』、東京銀行調査部訳、実業之日本社、1955年
『現代のポンド』、東京銀行調査部訳、至誠堂、1959年
『安定成長の通貨政策』、村野孝・海老沢道進訳、至誠堂、1960年
『景気変動と国際金融―応用動態経済学論集』、塩野谷九十九訳、東洋経済新報社、1963年
『国際通貨改革論』、堀江薫雄監訳、日本経済新聞社、1966年
『新しい経済政策』、館龍一郎監訳、竹内書店、1969年
『貨幣――歴史・理論・政策』、塩野谷九十九訳、東洋経済新報社、1974年
『社会科学とは何か』、清水幾太郎訳、岩波書店[岩波新書]、1975年
『経済動学』、宮崎義一訳、丸善、1976年
http://shark.lib.kagawa-u.ac.jp/kuir/file/5175/20120430173326/AN00038281_56_2_1.pdf
ケインズ、とハロッドの往復書簡と不安定性原理
篠崎敏雄
1 序
ケインズとハロッドとの聞で取り交わされた経済学に関する手紙は,『ケインズ全集』の第13巻と第14巻に収められている。ここで取り扱うのは,ハロッドの経済動学の体系の出発点であり,また近代的な経済成長理論の出発点ともなった,エコノミック・ジャーナルに載せられた「動学理論における一論」“An Essay in Dynamic Theory"(1939〉の原稿についての手紙である。ケインズは当時,エコノミツク・ジャ一ナルの編集者であり,それに投稿しようとしたハロッドの原稿に,手紙で詳細なコメントを与えた。それに対してハロッドも手紙で意見を述べ,さらにケインズから再び手紙が送られてくるという形で,6往復で,合計13通の手紙が遣り取りされている。
私にとって、歴史的にみて最も異常なことは、全体としての産出物に対する需給理論、すなわち雇用理論が……経済学では……完全に消滅したということです。『貨幣論』を刊行後、私にとっての最も重要な推移の一つは、突然この点に気づいたことでした。これは、所得が増大するとき、所得と消費のギャップは増大するであろうという心理法則――私自身の思考にとってはきわめて重要な結論でしたが、他の誰によっても明白にはこのように表現されたことのないものでした――を自ら言明した後に到来しました。それからかなり経ってから、流動性選好という意味での利子概念が浮かびました。これは、そのことに思いつくや否や、私の考えのなかでまったく明瞭なものになりました。そして最後に、非常に多くの混乱と多くの草稿の後、資本の限界効率という適正な概念が全体をうまく関連づけました(JMK. 14, p. 85)。
ハロッドのスタンスを知るのにわかりやすいのは、ロバートソンとの次のやり取りであろう。ロバートソンは、「もし[「発展する社会における資本の拡張」(一九三四年)で展開されている]あなたの論理が正しいのであれば、私が(ハイエクやその仲間とともに)この八年間述べようとしてきたことのすべてが無意味ということになります」と書いている。これに対しハロッドは、「私の唯一の陽光はメイナードの著作[『一般理論』]です。私は、彼の本が……画期的なものであるという点で、(あなたとは反対に)彼に同意[します]」と答えている。
往復書簡の発端。往復書簡に含まれる?:
ハロッド“An Essay in Dynamic Theory”(1938年草稿)
http://piketty.pse.ens.fr/files/Harrod1939.pdf
ハロッド“An Essay in Dynamic Theory”(1938年草稿)をめぐるハロッド=ケインズ往復書簡の解明(1) 中村, 隆之
発行日: Jan-2003
http://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/45534/1/10171103.pdf
ケインズの人物評:ロイ・ハロッドについて(一九三八年)
これ[「動学理論のエッセイ」]は、第一級のもので抜群に興味深いものです。あなたは非常に実り豊かな分析をしていると思います(ハロッド宛書簡、一九三八年八月一七日付。JMK. 14, p. 321)
純粋経済学者としても、宣伝係としても、オックスフォードで最良の人物です(ハロルド・マクミラン宛書簡、一九三九年二月二一日付。Skidelsky[1992]p. 696)。
ハロッドはまず「アンチノミー理論」として知られる経済成長論の提唱者として著名である。これはハロッド=ドーマー理論と呼ばれ、ケインズの理論を長期的かつ動学的なものにするという試み(右の第一文はその端緒となったハロッドの『エコノミック・ジャーナル』誌への投稿に対するケインズの第一声)であり、ロバート・ソローに代表される新古典派成長理論と対峙するものである。ケインズはハロッドを高く評価していた。『一般理論』を執筆中のケインズがゲラを送っだのもそのためである。彼らのあいだには多くのこの点をめぐる書簡のやり取りがなされている。
両者間の最も重要な争点は、古典派の利子理論をめぐるものであった。ケインズの立論の建設的部分には全面的に賛意を表しつつも、古典派の利子理論に対するケインズの批判的部分には反対の立場をハロッドはとっている。
『一般理論』との関係で、なかでも有名なのは、一九三六年八月のハロッド宛の手紙である。
これ[「動学理論のエッセイ」]は、第一級のもので抜群に興味深いものです。あなたは非常に実り豊かな分析をしていると思います(ハロッド宛書簡、一九三八年八月一七日付。JMK. 14, p. 321)
純粋経済学者としても、宣伝係としても、オックスフォードで最良の人物です(ハロルド・マクミラン宛書簡、一九三九年二月二一日付。Skidelsky[1992]p. 696)。
ハロッドはまず「アンチノミー理論」として知られる経済成長論の提唱者として著名である。これはハロッド=ドーマー理論と呼ばれ、ケインズの理論を長期的かつ動学的なものにするという試み(右の第一文はその端緒となったハロッドの『エコノミック・ジャーナル』誌への投稿に対するケインズの第一声)であり、ロバート・ソローに代表される新古典派成長理論と対峙するものである。ケインズはハロッドを高く評価していた。『一般理論』を執筆中のケインズがゲラを送っだのもそのためである。彼らのあいだには多くのこの点をめぐる書簡のやり取りがなされている。
両者間の最も重要な争点は、古典派の利子理論をめぐるものであった。ケインズの立論の建設的部分には全面的に賛意を表しつつも、古典派の利子理論に対するケインズの批判的部分には反対の立場をハロッドはとっている。
『一般理論』との関係で、なかでも有名なのは、一九三六年八月のハロッド宛の手紙である。
私にとって、歴史的にみて最も異常なことは、全体としての産出物に対する需給理論、すなわち雇用理論が……経済学では……完全に消滅したということです。『貨幣論』を刊行後、私にとっての最も重要な推移の一つは、突然この点に気づいたことでした。これは、所得が増大するとき、所得と消費のギャップは増大するであろうという心理法則――私自身の思考にとってはきわめて重要な結論でしたが、他の誰によっても明白にはこのように表現されたことのないものでした――を自ら言明した後に到来しました。それからかなり経ってから、流動性選好という意味での利子概念が浮かびました。これは、そのことに思いつくや否や、私の考えのなかでまったく明瞭なものになりました。そして最後に、非常に多くの混乱と多くの草稿の後、資本の限界効率という適正な概念が全体をうまく関連づけました(JMK. 14, p. 85)。
ハロッドのスタンスを知るのにわかりやすいのは、ロバートソンとの次のやり取りであろう。ロバートソンは、「もし[「発展する社会における資本の拡張」(一九三四年)で展開されている]あなたの論理が正しいのであれば、私が(ハイエクやその仲間とともに)この八年間述べようとしてきたことのすべてが無意味ということになります」と書いている。これに対しハロッドは、「私の唯一の陽光はメイナードの著作[『一般理論』]です。私は、彼の本が……画期的なものであるという点で、(あなたとは反対に)彼に同意[します]」と答えている。
往復書簡の発端。往復書簡に含まれる?:
ハロッド“An Essay in Dynamic Theory”(1938年草稿)
http://piketty.pse.ens.fr/files/Harrod1939.pdf
ハロッド“An Essay in Dynamic Theory”(1938年草稿)をめぐるハロッド=ケインズ往復書簡の解明(1) 中村, 隆之
発行日: Jan-2003
http://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/45534/1/10171103.pdf
こちらの方が読みやすい。
ハロッド動学のアンティノミー理論はなぜ失われたのか?
中村隆之 著 - 2002
https://www.jstage.jst.go.jp/article/jshet1963/41/41/41_41_58/_pdf
カレツキはハロッドの加速度原理を批判したらしいが、、、
http://eprints.lib.hokudai.ac.jp/dspace/bitstream/2115/31409/1/28%281%29_P139-169.pdf
_______
The Trade Cycle, An Essay(1936)
https://www.lib.city.kobe.jp/opac/opacs/find_detailbook?kobeid=CT%3A7200100575&mode=one_line&pvolid=PV%3A7200217957&type=CtlgBook
THE HUMAN FACTOR. 1. INVESTMENT AND OUTPUT. 53. INTEREST MONEY AND THE FOREIGN BALANCE. 110
The Trade Cycle: An Essay - Roy Harrod - Google Books books.google.co.jp/books
https://books.google.co.jp/books/about/The_trade_cycle.html?id=2zpBAAAAIAAJ
1 THE HUMAN FACTOR
4.The Monetary System
2 INVESTMENT AND OUTPUT
1.The Relation
2.The Multiprier ...
3 INTEREST MONEY AND THE FOREIGN BALANCE
4 THE QUESTION OF REMEDIES
1. Remedy and Diagnosis ...
Harrod, Roy, "Towards a Dynamic Economics", 1948
動態経済学序説 / R.F.ハロッド 著 ; 高橋長太郎, 鈴木諒一 共訳.
有斐閣, 1953.
http://dl.ndl.go.jp/info:ndljp/pid/3007641
目次
原著者序/p1
譯者序/p5
凡例/p9
第一講 動態經濟學の必要/p1
第二講 貯蓄の供給/p46
第三講 動態の基本定理/p85
第四講 (a)貿易差額/p135
第四講 (b)景氣對策/p155
第五講 利子とは陳腐か/p173
附錄/p216
http://hakase-jyuku.com/mankiw/category8/entry47.html
動学構築の必然性
一般に、「需要と供給の理論」で代表される伝統的な経済学は、一定の条件(個人の所得や嗜好等)のもとで、ある一組の価格体系が打ち立てられると想定している。これらは、現在では、一般に経済静学と呼ばれているが、ハロッドは、1936年に刊行した『景気循環論』の序文の中で、「純投資が存在する限り、社会の資本量と社会の所得取得能力とは、成長しつづけなければならないが、この成長の要因を静学的仮定の中に見出すことができない」と述べている。
かれの言う「純投資」とは資本減耗部分を差し引いた投資額を示している。静学においても、議論が事実と遊離しないように、各個人の行動のひとつの型として、個人は、いくばくかの貯蓄(所得の中から消費に向けられた分を差し引いたもの)を行うものと想定している。ケインズの理論によれば、貯蓄が存在すれば、定義からそれと同額の投資が存在する。純投資が存在すれば、社会全体の生産能力は増加しているはずなので、静学で想定しているように、所得一定の条件を想定することはできない。つまり、貯蓄が存在すると想定する以上、生産能力が絶えず成長し続けることを想定していなければ、論理的に整合的でないとハロッドは考えていた。そこから、より現実的な経済学を構築するには、所得の増加率、つまり、経済成長率そのものを決定する理論の必要性があるとかれは考えるようになった。
ハロッドは、その後、1939年の『エコノミック・ジャーナル』誌上の「動態理論の一試論("An Essay in Dynamic Theory")」という経済成長理論の記念碑的な論文の中で、
(1) 貯蓄(S)は、主に、所得額(Y)の大きさに応じて決まり、
(2) 投資(I)は、主に、所得の増加額の大きさに応じて決まり、
(3) 事後的にみると、投資は貯蓄と等しい。
という基本的な関係をもとに、
S=sY、I=CΔY、I=Sという数式から、
経済成長率G(=ΔY/Y)=s/C
という関係式を見出した。(sは所得の中で貯蓄される割合、Cは投資と所得の増加額との割合。後者の関係は、後に「加速度因子または係数」と呼ばれるようになるが、『景気循環論』では単に「リレーション(関係)」とかれは呼んでいた)
かれは、このGを「現実成長率(the actual rate of growth)」と呼んでいるが、そのGの値は、その時々の経済情勢により当然のことながら変動する。従って、Gが変われば、sまたはCの値も変わっているはずで、s(貯蓄率)やC(投資率、後に「資本係数」と呼ばれるようになった)が一定であるとは想定されていない。
ハロッドは、各経済主体(家計や企業)が満足するsやCが存在すると考えて、それぞれ、sd(望ましい貯蓄率)、Cr(必要とされる投資率)という概念を導入し、それらが満たされ、しかも、社会全体でS=Iという財市場の均衡が実現されたときの成長率として「保証成長率(the warranted rate of growth)」Gwを提示した。
Gw=sd/Cr
これが、動学の基本方程式と呼ばれるもので、ハロッドは、このGwとGの大小関係で、各経済主体の行動パターンを整理した。Gw>Gの場合、sd>s、または、Cr<Cという関係が考えられ、家計は望んでいたよりも貯蓄が少ないので、より貯蓄を増やす(消費を削る)ように行動し、企業は、必要とされる投資よりも多く投資してしまったと感じ、投資額を削減しようと行動すると考えた。その結果、現実の成長率(G)は、益々、下がる傾向が強まり、GwとGの乖離はさらに広がると考えた。これが有名なハロッドの「不安定性の原理(Instability Principle)」である。
各経済主体が、計画を立てながら貯蓄や投資を行っていると考えると、このような乖離そのものが何故発生するのか疑問を感じる方もいると思われるが、企業が設備投資を行い、生産量を増加させたとしても、思ったよりも製品が売れずに在庫が増えたという状況は、よくある話である。固定資産のほかに在庫等の流動資産も経済学でいう「資本」の構成要素であるから、資本の増加分である投資も増加する。従って、「事後的に」Cr<Cであると企業が感じることはよくあることではないだろうか。家計の場合は、主に、所得が思ったよりも下がったり、予想しなかった支出が発生したりして、sd>sと判断することがあると思われる。
また、ハロッドは、たとえ、Gw=Gが実現されたとしても、社会全体が最適な状況とは限らないと考えた。これは、各企業や家計自らが望ましい生産活動(利益極大)や消費活動(効用極大)を行ったとしても、必ずしも完全雇用が実現されるとは限らないというケインズの考えに沿っている。社会全体が最適になるには、少なくとも、完全雇用が実現されてなければならない。人口の増加や技術革新を考慮に入れると、完全雇用が達成された場合に実現される成長率が存在すると考えられる。これが、ハロッドの「自然成長率(the natural rate of growth)」Gnで、政府は、経済政策を行ううえで、このGwをGnに近づける必要性があると説いた。ハロッドが1973年に出版した『経済動学』では、GとGwとGnの大小関係から、拡張主義的政策の影響とその是非が詳細に議論されている。
これらの経済動学の議論が「各国の経済政策に関する公理についての合意」になることをハロッド自身は望んでいたが、残念ながら、そのようにはならなかった。Gwの概念がなかなか他の経済学者に理解されなかったことと、GwやGnの実際的な測定の困難さが災いしていたような気がする。
保証成長率の概念の難しさ
米国のノーベル経済学賞受賞者のロバート・ソローは、1956年に公表した論文「経済成長理論への一寄与」の中で、ハロッドが展開した「不安定性原理」をGwとGn間のものと誤解した上に、さらに、ハロッドの議論が「資本係数(Cr)」の硬直性を前提としていると思い込み、Crの硬直性を排除した理論を組み立て、GwとGnが一致する可能性を例示し、ハロッドの「不安定性原理」は誤っていると特徴付けた。このことが、ハロッド理論の性格を決定付け、その後の経済学の教科書の記述内容を歪めてしまった。…
経験の原理
ハロッドがこの「帰納法の妥当性」の証明として用意したのが、かれの言う「経験の原理(The Principle of Experience)」であるが、独創的な論証方法であったがために、専門的な哲学者から無視されることとなった。それは一体どのようなものだったのか。
かれは、この世の中には連続性があるという前提から議論を始める。「私たちが住んで来た世界が連続性を含んでおりませんでしたら、どんな方法を用いても、世界について何等の知識も得られなかったでしょう」と、かれの『社会科学とは何か』という書物の中で述べている。「連続性」というと分かりにくいが、要するに同じ事象が再現することで、あるAという前提のもとでBが発生するという個別の事象が何度も再現するところから、AならばBであるという一般的な法則、つまり知識を得ることができる訳で、このような事象の再現が全くない世界では、何等、知識は得られないとハロッドは考えている。
ハロッドは、このような、ある連続性を含む「連続体」を旅している旅行者の立場に立って議論を進めている。この旅行者はこの「連続体」がどこまで続くのか、どのような大きさなのか等について何の知識もない「完全に無知な人(Homo Ignorans)」であるという前提に立っている。この連続体の旅行は、遠い過去から連綿と続き将来へと伸びていく。
その最初の基点をA点とし、この旅行が終了する時点、つまり、連続性が途切れた時点をBとすると、AB線がこの旅行の全工程を示す。この旅行者は、このAB上のどこかの時点から旅行を開始し、この連続性が続くかどうかという質問を発していく。ハロッドは、このABを(X+1)等分に均等に分割し、その単位ごとに旅行者が「連続性が続いているか」との問いを発した場合に、正しい答えが返ってくる「確率」を問題にする。
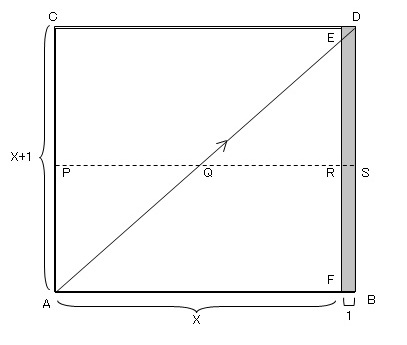
図1、『帰納法論理の基礎』p.56より採録(但し、ABCDEFの記号は採録者が追記)
横軸のABと同じ長さの縦軸ACを引くと、ABCDの正方形が出来上がる。横軸は、質問の数、縦軸で過去から将来に渡って旅行者が確認をしてきた答えの数を表す。この旅行者が確認している現時点をP点とし、そこからABに平行して線を引き、対角線との交点をQとすると、PQは今までに連続性があったという正しい答えが返ってきた数を、QSは将来の答えの数を示す。この旅行に終わり、つまり、連続性が途切れるときがあるとすると、その場合に正しい答えが返ってくる確率は、X/(X+1)となる。
この旅行者が、連続体の旅行の中で、将来正しい答えを得る確率は、QS間で正しい答えを得る確率であるが、ハロッドは、この旅行者はQS(将来の答え)とQR(正しい将来の答え)の比率(QR/QS)も連続体そのものの長さも知ることができなので、これを確率に使うべきでないとして、△AEF÷△ADBの比率が求める確率となるべきだという。その値を計算すると、X2/(X+1)2となる。これが正しければ、連続体が経過する時間(X)が長ければ長いほど、その確率は高くなる。
ハロッドの議論はこのように、かなり込み入ってはいるが、要するに、ある事象が再現する頻度が高ければ高いほど、その確率は高くなるということで、ある意味では、常識的な結論ではないか思う。ハロッドはこのことを「連続体の確率逓増の法則(the law of increasing probability of continuance)」と呼び、これこそが「経験の原理」であると言う。この議論の中でハロッドは、この連続体の旅行の端にいる可能性は「ありそうもない(unlikely)」と考え、上記のXの値が限りなく大きな値となることを想定している。
かれは、①連続性がなければこの世の中の個別に事象から一般的な法則(知識)は得られない、②その連続性が持続する時間が長ければ長いほどその確率は高くなり信頼性は増す、③その意味で、帰納法の最も根本的な手続きは、表面的に一致する事例をもついくつかに事例を列挙して一般的な結論に導く「単純枚挙法(the method of simple enumeration)」であるとの結論に達した。
経験重視の経済学を求めて
生粋の経験主義者であったF.Y.エッジワースのもと、経験を重視した経済学を身につけたハロッドは、一貫して現実のさまざまな事象から丹念に思索を重ね、より一般的で普遍的な経済原理の樹立を求めてきた。そのひとつの例が「ハロッドの二分法」と呼ばれる提起ではなかったか。それは、まさに、上で言及した「帰納法」の手続きを「応用哲学」である経済学に適用してきたといっていい。
『経済動学』の最終章で、ハロッドは、今後、経済学者がなすべきこととして、以下のように述べている。
「まず第一に、われわれは経済動学の基本公理について、アルフレッド・マーシャルとパレートが定式化し、のちに「不完全競争」の理論によって修正をうけたミクロ静学の公理をお手本として、合意の成立をはかる必要があるということである。第二に、その公理から派生するものとして、各国の経済政策に関する公理について合意の成立をはかる必要があるということである。各種の政策を開始するにあたって公表された理論づけを見ると、現代経済動学の視点が全く欠落しているのが常だからである。第三に、そして最後に、われわれは、動学理論とその実践的応用とに関連する事実の流れを評価する方法を確立する必要があるということである。今日まで、最高の政策担当者によって示された政策の説明と理由づけは、非常に不十分なもののように思われる」
[参考文献]
1.Besomi, Daniele(ed.), The Collected Interwar Papers and Correspondence of Roy Harrod", 2003
2.Eltis, Walter, "Roy Harrod and the Keynesian revolution: his newly published correspondence", The European Journal of the History of Economic Thought, 2005
3.Harrod, Roy, "The Trade Cycle: An Essay", 1936(宮崎義一、浅野栄一訳『景気循環論』東洋経済新報社、1955年)
4.Harrod, Roy, "An Essay in Dynamic Theory", The Economic Journal, 1939
5.Harrod, Roy, "Memory", Mind, 51, 1942
6.Harrod, Roy, "Towards a Dynamic Economics", 1948(高橋長太郎、鈴木諒一訳『動態経済学序説』有斐閣、1953年)
7.Harrod, Roy, "Induction and Probability", Philosophy, 26, 1951
8.Harrod, Roy, "The Life of John Maynard Keynes", 1951(塩野谷九十九訳『ケインズ伝』東洋経済新報社、1954年)
9.Harrod, Roy, "Foundations of Inductive Logic", 1956
10.Harrod, Roy, "Towards a New Economic Policy", 1967(舘龍一郎監訳『新しい経済政策』竹内書店、1969年)
11.Harrod, Roy, "Sociology, Morals and Mystery",1972(清水幾太郎訳『社会科学とは何か』岩波新書、1975年)
12.Harrod, Roy, "Economic Dynamics", 1973(宮崎義一訳『経済動学』丸善、1976年)
13.伊東光晴『現代に生きるケインズ-モラル・サイエンスとしての経済理論-』岩波新書、2006年
14.Keynes, John Maynard, "A Treatise on Probability", 1921
15.Keynes, John Maynard, "Essays in Biography", 1933(熊谷尚夫、大野忠男訳『人物評伝』岩波書店、1959年)
16.Keynes, John Maynard, "The General Theory of Employment, Interest and Money", 1936(塩野谷九十九訳『雇用・利子および貨幣の一般理論』東洋経済新報社、1941年)
17.黒田東彦「『ある論争』で素顔をみたハロッド卿の思い出-インフレと不況の共存に新理論-」『エコノミスト』1991年9月10日号
18.Moggridge, Donald(ed.), "The Collected Writings of John Maynard Keynes Vol.XIV The General Theory and After", 1973
19.Rampa, Giorgio, Luciano Stella and A. P. Thirwall(ed.), "Economic Dynamics, Trade and Growth: Essays on Harrodian Themes", 1998
20.斎藤隆子「ハロッドの『経験の原理』と帰納法:ケインズの帰納法と比較して」『経済学史学会年報』第39号、2001年
21.Solow, Robert, "A Contribution to the Theory of Economic Growth", Quarterly Journal of Economics, 1956(福岡正夫、神谷伝造、川又邦雄訳『資本・成長・技術進歩』竹内書店、1970年)
22.Young, Warren, "Interpreting Mr Keynes - The IS-LM enigma", 1987(富田洋三、中島守善訳『IS-LMの謎-ケインズ経済学の解明』多賀出版、1994年)
23.Young, Warren and Frederic S. Lee, "Oxford Economics and Oxford Economists", 1993
ハロッド動学のアンティノミー理論はなぜ失われたのか?
中村隆之 著 - 2002
https://www.jstage.jst.go.jp/article/jshet1963/41/41/41_41_58/_pdf
カレツキはハロッドの加速度原理を批判したらしいが、、、
http://eprints.lib.hokudai.ac.jp/dspace/bitstream/2115/31409/1/28%281%29_P139-169.pdf
_______
The Trade Cycle, An Essay(1936)
https://www.lib.city.kobe.jp/opac/opacs/find_detailbook?kobeid=CT%3A7200100575&mode=one_line&pvolid=PV%3A7200217957&type=CtlgBook
THE HUMAN FACTOR. 1. INVESTMENT AND OUTPUT. 53. INTEREST MONEY AND THE FOREIGN BALANCE. 110
| 書名 | 景気循環論||ケイキ ジュンカンロン |
|---|---|
| 著者 | Harrod, Roy Forbes, Sir, 1900-1978 |
| 著者 | 宮崎, 義一(1919-)||ミヤザキ, ヨシカズ |
| 出版 | 東京 : 中央公論新社 , 2011.11 |
| 大きさ | 22, ix, 183p ; 18cm |
| シリーズ名 | 中公クラシックス:W68 |
| 出版国 | Japan (日本) |
| 注記 | 中公バックス「世界の名著」69『ケインズ, ハロッド』(1980年刊) のハロッド著『景気循環論』の第1章、第2章を収載 |
| 注記 | 年譜: p167-181 |
| 分類 | NDC8:337.9 |
| 分類 | NDC9:337.9 |
| 件名 | 景気||ケイキ |
| ISBN | 9784121601292 |
| 問い合わせ番号 | PV:7200217957 |
| 請求記号 | 市立 3379=P1= |
| 内容説明 | ケインズの乗数理論と加速度原理を組み合わせたハロッド動学を初めて提示した、画期的な名著。ロビンソン・クルーソー経済、独立生産者の交換経済、円滑な発展の維持不可能性などについて論考する。 【著者紹介】 〈ハロッド〉1900〜78年。イギリスの経済学者。ケインズの高弟の一人でその思想の継承者。著者に「ケインズ伝」など。 Copyright(C) 1995-2004 |
The Trade Cycle: An Essay - Roy Harrod - Google Books books.google.co.jp/books
https://books.google.co.jp/books/about/The_trade_cycle.html?id=2zpBAAAAIAAJ
1 THE HUMAN FACTOR
4.The Monetary System
2 INVESTMENT AND OUTPUT
1.The Relation
2.The Multiprier ...
3 INTEREST MONEY AND THE FOREIGN BALANCE
4 THE QUESTION OF REMEDIES
1. Remedy and Diagnosis ...
The Trade Cycle, An Essay(1936):
http://dl.ndl.go.jp/info:ndljp/pid/3020415
景気循環論
著者 R.F.ハロッド 著[他]
出版者 東洋経済新報社
出版年月日 1963(1955とほぼ同じ。中公は1、2章のみ)
目次
序文
日本版への序
凡例
第一章 人間的要因/p1
I 予備的考察/p1
II 分業/p14
III 資本主義/p27
IV 貨幣制度/p40
第二章 投資と産出量/p60
I リレーション/p60
II 乗数/p72
III 物価と利潤の動き/p83
IV 三つの動学的決定要因/p97
V 景気循環の不可避性/p112
補論 貯蓄にかんする覚え書/p118
第三章 利子・貨幣および国際収支/p123
I 利子率/p123
II 貨幣/p141
III 国際収支/p163
第四章 治療の問題/p178
I 治療と診断/p178
II 安定貨幣/p193
III 公共事業と財政/p214
IV 補助金/p251
訳者注/p261
訳者あとがき/p271
事項索引/p0
人名索引/p0
引用書名索引/p0
_________
http://dl.ndl.go.jp/info:ndljp/pid/3020415
景気循環論
著者 R.F.ハロッド 著[他]
出版者 東洋経済新報社
出版年月日 1963(1955とほぼ同じ。中公は1、2章のみ)
目次
序文
日本版への序
凡例
第一章 人間的要因/p1
I 予備的考察/p1
II 分業/p14
III 資本主義/p27
IV 貨幣制度/p40
第二章 投資と産出量/p60
I リレーション/p60
II 乗数/p72
III 物価と利潤の動き/p83
IV 三つの動学的決定要因/p97
V 景気循環の不可避性/p112
補論 貯蓄にかんする覚え書/p118
第三章 利子・貨幣および国際収支/p123
I 利子率/p123
II 貨幣/p141
III 国際収支/p163
第四章 治療の問題/p178
I 治療と診断/p178
II 安定貨幣/p193
III 公共事業と財政/p214
IV 補助金/p251
訳者注/p261
訳者あとがき/p271
事項索引/p0
人名索引/p0
引用書名索引/p0
_________
Harrod, Roy, "Towards a Dynamic Economics", 1948
動態経済学序説 / R.F.ハロッド 著 ; 高橋長太郎, 鈴木諒一 共訳.
有斐閣, 1953.
http://dl.ndl.go.jp/info:ndljp/pid/3007641
目次
原著者序/p1
譯者序/p5
凡例/p9
第一講 動態經濟學の必要/p1
第二講 貯蓄の供給/p46
第三講 動態の基本定理/p85
第四講 (a)貿易差額/p135
第四講 (b)景氣對策/p155
第五講 利子とは陳腐か/p173
附錄/p216
_________
ロイ・ハロッド卿(1900~1978)はケインズ経済学の静学的限界を打破して経済動学を創立した世界的な経済学者としてよく知られています。
1978年、ハロッドが亡くなった後、膨大な文書と蔵書がノーフォーク州ホルトにある彼の家に残されました。
1984年、その一部(書簡を中心とした文書約15,000葉)を本学(千葉商科大)が購入し、保存・活用することになりました。
http://www.lib.cuc.ac.jp/search/roy.html
http://www.nbs.sk/_img/Documents/BIATEC/BIA12_02/25_28.pdf
http://hakase-jyuku.com/mankiw/category8/entry47.html
ハロッドモデル(経済成長理論)
Kさんからいただいた論文の抜粋です。
------------------------------------------------------------
加速度原理と「ハロッドのナイフの刃」
------------------------------------------------------------
(北山孝信,2001,「ケインズ経済学の限界について(サムエルソン
と新古典派総合)」,福井県立大学修士論文,第2章より)
----------
■加速度原理
----------
不況期に財政支出を拡大する政策は、ISギャップを均衡させる
に過ぎず、この枠組では、高度成長は説明できない。
サムエルソンの成長理論の源泉は、加速度原理であった。
『経済学』の枠組みで、簡単に説明すると、社会が必要とする資本
ストックは、主として所得または生産の水準に依存し、資本ストッ
クへの追加分(純投資)は、所得が成長している時のみおこる。
その結果、好況期は、消費財の売上減のみならず、売上が横ばい、
あるいは以前より低成長になっただけで終わりがくる、というもの
だ。
この加速度原理は、政府の適度な市場介入により、成長が永遠に
続くことを前提としている。
その永遠の成長の前提となるケインズ派の成長モデルが、ロイ・
フォーブス・ハロッドの「ハロッドモデル」であった。
----------
■ハロッドモデル
----------
「ハロッドのナイフの刃」と称されることもあるハロッドモデルにつ
いて考えていく。
ハロッドモデルの基本式は、
経済成長率 G(=ΔY/Y)=s/C …①
である。
sは所得のうち貯蓄に回される割合である。この貯蓄Sは、投資
Iと均衡している(ハロッドモデルは、IS均衡を前提としている
(ハロッドの前提①)ので、貯蓄の高まりは、投資の高まりと同義で
ある。
次に、ハロッドは保証成長率を提示する。
保証成長率 Gw=sd/C …②
sdは各社会を構成する人々が、その時点で貯蓄しようとする割
合である。
これにより、国民経済は、保証される成長率をえる。なぜか?
ハロッドは、政府が経済活動に介入することで、市場経済が上手
く立ちまわることを確信している(ハロッドの前提②)。
よって、一時的に投資が抑制されても、財政政策等をとることで、
常に市場参加者が、将来に楽観的見とおしをもち、投資は結果的に
もとに戻り、経済は拡大するからだ。
また、ハロッドは、行き過ぎた投資も政府の介入により御しえる
と考えている。よって、一時的に不均衡が生じたとしても、長期的
にはISバランスは均衡することとなる。
もう少し貯蓄が増えると経済が成長するか考えよう。
経済学上において、投資は生産設備等、購入後も残って蓄積され、
以後も生産に寄与するものをさしている。
我々の投資は、株等の購入を意味するが、それは我々の貯蓄が、
株をとおして企業に貸付られたに過ぎない。企業が、銀行をとおし
て資金を調達したか、株式市場をとおして調達したかの違いしかな
い。
企業が設備等を投入してはじめて投資となる。よって、食料や衣
服等、購入して使えば何も残らない、もしくは、その後の生産に寄
与しないものは、消費になる。
ちょっと歴史の勉強をしよう。戦前の日本には地主がいた。
彼等はいきなり地主になったわけではない。
江戸時代、百姓でも水呑百姓は、年貢を払ってのこりの米で細々
と生活していた。
彼等には、余剰が残る余地がなかった。しかし、もともと土地を
もっていた本百姓たちは、大名に年貢は取られるが、水呑よりは余
裕があった。
そこで才覚のあったものが、千羽ごき等の作業が楽になるものに
投資し、それにより生じた労働余剰などを、当時需要が拡大しつつ
あった綿を作り売ることで、財を成していった。
それにより、もっと人を使って売れるものの生産を拡大し、また
上手くいかなかった者の土地を購入することを通じて、「さま」付
の大地主が形成されることとなった。
ここからも明らかなように、江戸時代や戦前の小作のように、せ
っかく作った米のほとんどを年貢(地代)にとられていては、いくら
生産が拡大できるトラクターや肥料があっても、とてもそれを買え
ないことはわかるだろう。
今日でも途上国では、食べるのに精一杯で、とても投資に回らな
い国が多く存在する。
人は、何にもまして食べることを優先する。腹いっぱい食べるこ
とができて、はじめて違うものに手を出せるのである。
ハロッドの保証成長モデルは、このことを正に前提にしているの
である。
ハロッドの第二の基本式は、
自然成長率 Gn=労働成長率+技術進歩率 …③
である。
ここでの技術進歩率は、投資の拡大、蓄積に依存しているので、
自然成長率 Gn=so/Cr …④ と書きかえることができる。
ここでのsoは、自然成長率Gnに必要な人口成長と技術進歩に見
あった貯蓄率である。
ハロッドは、財政、金融政策により貯蓄率を調整し、経済の潜在
的成長率と調和する完全雇用と成長を合理的に維持するための過不
足ない貯蓄率を提供すると考えているので、これにより、経済は拡
大しつづけることができる。
次にハロッドのナイフの刃について考えよう。現実の成長率が保
証成長率を上回った時(G>Gw)、s>sdもしくはC<Crの時、
もしくは両方である。この場合、
G>Gw s↑=ΔI↑ ΔY↑
ΔC↑ (需要増) …⑤
(ΔS↑) ΔI↑
と投資、所得、消費と投資、さらにまた所得と限りなく拡大循環を
うみ、これにより、ますます、現実の成長率Gは、保証成長率Gw
から乖離していくことになる。
逆もまた真なりで、ますます下方へ乖離する。
ハロッドは、現実成長率が下回る場合の「底」は、難解な問題だ
とするが、現実社会においては、政府当局が金融・財政政策により
重大な落ち込みを防ぐため、この問題は緊急性をもたないとしてい
る。
また拡大期においては、資本の蓄積等のより、成長率は保証成長
率を上回り、元の均衡に戻らない、としている。
このように見ていくと「ハロッドモデルはなんなのか?」と思う
ことだろう。
現実の成長率が保証成長率と乖離していくのであれば「保証成長
率そのものが何なのか?」ということになる。
このような、ハロッドモデルの不安定性に対し、真っ向から異論
を唱えたのが、ロバート・ソローだった。
ハロッドは政府の介入により経済成長を維持しうることを大前提
しているが、これは正にバブルの論理である。
政府の市場介入、財政・金融政策の対し、市場参加者が信認を失
えば、将来の見通しは悲観的なものとなり、経済は成長できなくな
ってしまう。
ハロッドのモデルにしても、サムエルソンにしても、財政・金融
政策により不況期に適度に需要を喚起することで、国民が国民経済
に対し、楽観的見とおしをもつことを大前提とした。
事実、60年代までは、高度成長を謳歌し、永遠にこのような成長
が続くと考えられ、多くの人々が将来に楽観視した。
70年代に入ると政府の失敗等の弊害が目立ちはじめ、これまでな
ら上手くいったはずの、不況期の財政策でも高成長は元に戻らなか
った。
結果、フリードマン等市場を万能とする自由主義者、政府懐疑派
の影響力が強まることとなった。
「スタグフレーション」という厳然たる事実のもと、政府の財政政
策の神秘性は喪失し、ハロッド、サムエルソンが前提とした「将来
への楽観見通し」も崩壊した。
彼らの枠組みは、所詮「バブルの論理」だった。重要なことは、
成長するという「将来への期待」でなく「何故成長するか?」であ
り「成長のために何をなしうるか?」ということだったのである。
こうして、新古典派総合は、70年代急速に影響力を喪失すること
となった。
----------
■参考
----------
将来的に、不況になっても政府の介入により、成長が維持できる
(ΔY↑)と考えれば、企業は物が売れると期待し、投資を増やして
いく。一般の人々も消費を増やしていく。
しかし「上手くいかない」と考えれば、消費も投資も抑制される。
財政拡大によりISギャップは、一時的にリカバリーできるが、
将来見通しが悲観的であれば、企業も人々も消費と投資を抑制する。
結果、赤字国債は累積することとなる。
NEXT:経済変動の説明
------------------------------------------------------------
加速度原理と「ハロッドのナイフの刃」
------------------------------------------------------------
(北山孝信,2001,「ケインズ経済学の限界について(サムエルソン
と新古典派総合)」,福井県立大学修士論文,第2章より)
----------
■加速度原理
----------
不況期に財政支出を拡大する政策は、ISギャップを均衡させる
に過ぎず、この枠組では、高度成長は説明できない。
サムエルソンの成長理論の源泉は、加速度原理であった。
『経済学』の枠組みで、簡単に説明すると、社会が必要とする資本
ストックは、主として所得または生産の水準に依存し、資本ストッ
クへの追加分(純投資)は、所得が成長している時のみおこる。
その結果、好況期は、消費財の売上減のみならず、売上が横ばい、
あるいは以前より低成長になっただけで終わりがくる、というもの
だ。
この加速度原理は、政府の適度な市場介入により、成長が永遠に
続くことを前提としている。
その永遠の成長の前提となるケインズ派の成長モデルが、ロイ・
フォーブス・ハロッドの「ハロッドモデル」であった。
----------
■ハロッドモデル
----------
「ハロッドのナイフの刃」と称されることもあるハロッドモデルにつ
いて考えていく。
ハロッドモデルの基本式は、
経済成長率 G(=ΔY/Y)=s/C …①
である。
sは所得のうち貯蓄に回される割合である。この貯蓄Sは、投資
Iと均衡している(ハロッドモデルは、IS均衡を前提としている
(ハロッドの前提①)ので、貯蓄の高まりは、投資の高まりと同義で
ある。
次に、ハロッドは保証成長率を提示する。
保証成長率 Gw=sd/C …②
sdは各社会を構成する人々が、その時点で貯蓄しようとする割
合である。
これにより、国民経済は、保証される成長率をえる。なぜか?
ハロッドは、政府が経済活動に介入することで、市場経済が上手
く立ちまわることを確信している(ハロッドの前提②)。
よって、一時的に投資が抑制されても、財政政策等をとることで、
常に市場参加者が、将来に楽観的見とおしをもち、投資は結果的に
もとに戻り、経済は拡大するからだ。
また、ハロッドは、行き過ぎた投資も政府の介入により御しえる
と考えている。よって、一時的に不均衡が生じたとしても、長期的
にはISバランスは均衡することとなる。
もう少し貯蓄が増えると経済が成長するか考えよう。
経済学上において、投資は生産設備等、購入後も残って蓄積され、
以後も生産に寄与するものをさしている。
我々の投資は、株等の購入を意味するが、それは我々の貯蓄が、
株をとおして企業に貸付られたに過ぎない。企業が、銀行をとおし
て資金を調達したか、株式市場をとおして調達したかの違いしかな
い。
企業が設備等を投入してはじめて投資となる。よって、食料や衣
服等、購入して使えば何も残らない、もしくは、その後の生産に寄
与しないものは、消費になる。
ちょっと歴史の勉強をしよう。戦前の日本には地主がいた。
彼等はいきなり地主になったわけではない。
江戸時代、百姓でも水呑百姓は、年貢を払ってのこりの米で細々
と生活していた。
彼等には、余剰が残る余地がなかった。しかし、もともと土地を
もっていた本百姓たちは、大名に年貢は取られるが、水呑よりは余
裕があった。
そこで才覚のあったものが、千羽ごき等の作業が楽になるものに
投資し、それにより生じた労働余剰などを、当時需要が拡大しつつ
あった綿を作り売ることで、財を成していった。
それにより、もっと人を使って売れるものの生産を拡大し、また
上手くいかなかった者の土地を購入することを通じて、「さま」付
の大地主が形成されることとなった。
ここからも明らかなように、江戸時代や戦前の小作のように、せ
っかく作った米のほとんどを年貢(地代)にとられていては、いくら
生産が拡大できるトラクターや肥料があっても、とてもそれを買え
ないことはわかるだろう。
今日でも途上国では、食べるのに精一杯で、とても投資に回らな
い国が多く存在する。
人は、何にもまして食べることを優先する。腹いっぱい食べるこ
とができて、はじめて違うものに手を出せるのである。
ハロッドの保証成長モデルは、このことを正に前提にしているの
である。
ハロッドの第二の基本式は、
自然成長率 Gn=労働成長率+技術進歩率 …③
である。
ここでの技術進歩率は、投資の拡大、蓄積に依存しているので、
自然成長率 Gn=so/Cr …④ と書きかえることができる。
ここでのsoは、自然成長率Gnに必要な人口成長と技術進歩に見
あった貯蓄率である。
ハロッドは、財政、金融政策により貯蓄率を調整し、経済の潜在
的成長率と調和する完全雇用と成長を合理的に維持するための過不
足ない貯蓄率を提供すると考えているので、これにより、経済は拡
大しつづけることができる。
次にハロッドのナイフの刃について考えよう。現実の成長率が保
証成長率を上回った時(G>Gw)、s>sdもしくはC<Crの時、
もしくは両方である。この場合、
G>Gw s↑=ΔI↑ ΔY↑
ΔC↑ (需要増) …⑤
(ΔS↑) ΔI↑
と投資、所得、消費と投資、さらにまた所得と限りなく拡大循環を
うみ、これにより、ますます、現実の成長率Gは、保証成長率Gw
から乖離していくことになる。
逆もまた真なりで、ますます下方へ乖離する。
ハロッドは、現実成長率が下回る場合の「底」は、難解な問題だ
とするが、現実社会においては、政府当局が金融・財政政策により
重大な落ち込みを防ぐため、この問題は緊急性をもたないとしてい
る。
また拡大期においては、資本の蓄積等のより、成長率は保証成長
率を上回り、元の均衡に戻らない、としている。
このように見ていくと「ハロッドモデルはなんなのか?」と思う
ことだろう。
現実の成長率が保証成長率と乖離していくのであれば「保証成長
率そのものが何なのか?」ということになる。
このような、ハロッドモデルの不安定性に対し、真っ向から異論
を唱えたのが、ロバート・ソローだった。
ハロッドは政府の介入により経済成長を維持しうることを大前提
しているが、これは正にバブルの論理である。
政府の市場介入、財政・金融政策の対し、市場参加者が信認を失
えば、将来の見通しは悲観的なものとなり、経済は成長できなくな
ってしまう。
ハロッドのモデルにしても、サムエルソンにしても、財政・金融
政策により不況期に適度に需要を喚起することで、国民が国民経済
に対し、楽観的見とおしをもつことを大前提とした。
事実、60年代までは、高度成長を謳歌し、永遠にこのような成長
が続くと考えられ、多くの人々が将来に楽観視した。
70年代に入ると政府の失敗等の弊害が目立ちはじめ、これまでな
ら上手くいったはずの、不況期の財政策でも高成長は元に戻らなか
った。
結果、フリードマン等市場を万能とする自由主義者、政府懐疑派
の影響力が強まることとなった。
「スタグフレーション」という厳然たる事実のもと、政府の財政政
策の神秘性は喪失し、ハロッド、サムエルソンが前提とした「将来
への楽観見通し」も崩壊した。
彼らの枠組みは、所詮「バブルの論理」だった。重要なことは、
成長するという「将来への期待」でなく「何故成長するか?」であ
り「成長のために何をなしうるか?」ということだったのである。
こうして、新古典派総合は、70年代急速に影響力を喪失すること
となった。
----------
■参考
----------
将来的に、不況になっても政府の介入により、成長が維持できる
(ΔY↑)と考えれば、企業は物が売れると期待し、投資を増やして
いく。一般の人々も消費を増やしていく。
しかし「上手くいかない」と考えれば、消費も投資も抑制される。
財政拡大によりISギャップは、一時的にリカバリーできるが、
将来見通しが悲観的であれば、企業も人々も消費と投資を抑制する。
結果、赤字国債は累積することとなる。
NEXT:経済変動の説明
_________
動学構築の必然性
一般に、「需要と供給の理論」で代表される伝統的な経済学は、一定の条件(個人の所得や嗜好等)のもとで、ある一組の価格体系が打ち立てられると想定している。これらは、現在では、一般に経済静学と呼ばれているが、ハロッドは、1936年に刊行した『景気循環論』の序文の中で、「純投資が存在する限り、社会の資本量と社会の所得取得能力とは、成長しつづけなければならないが、この成長の要因を静学的仮定の中に見出すことができない」と述べている。
かれの言う「純投資」とは資本減耗部分を差し引いた投資額を示している。静学においても、議論が事実と遊離しないように、各個人の行動のひとつの型として、個人は、いくばくかの貯蓄(所得の中から消費に向けられた分を差し引いたもの)を行うものと想定している。ケインズの理論によれば、貯蓄が存在すれば、定義からそれと同額の投資が存在する。純投資が存在すれば、社会全体の生産能力は増加しているはずなので、静学で想定しているように、所得一定の条件を想定することはできない。つまり、貯蓄が存在すると想定する以上、生産能力が絶えず成長し続けることを想定していなければ、論理的に整合的でないとハロッドは考えていた。そこから、より現実的な経済学を構築するには、所得の増加率、つまり、経済成長率そのものを決定する理論の必要性があるとかれは考えるようになった。
ハロッドは、その後、1939年の『エコノミック・ジャーナル』誌上の「動態理論の一試論("An Essay in Dynamic Theory")」という経済成長理論の記念碑的な論文の中で、
(1) 貯蓄(S)は、主に、所得額(Y)の大きさに応じて決まり、
(2) 投資(I)は、主に、所得の増加額の大きさに応じて決まり、
(3) 事後的にみると、投資は貯蓄と等しい。
という基本的な関係をもとに、
S=sY、I=CΔY、I=Sという数式から、
経済成長率G(=ΔY/Y)=s/C
という関係式を見出した。(sは所得の中で貯蓄される割合、Cは投資と所得の増加額との割合。後者の関係は、後に「加速度因子または係数」と呼ばれるようになるが、『景気循環論』では単に「リレーション(関係)」とかれは呼んでいた)
かれは、このGを「現実成長率(the actual rate of growth)」と呼んでいるが、そのGの値は、その時々の経済情勢により当然のことながら変動する。従って、Gが変われば、sまたはCの値も変わっているはずで、s(貯蓄率)やC(投資率、後に「資本係数」と呼ばれるようになった)が一定であるとは想定されていない。
ハロッドは、各経済主体(家計や企業)が満足するsやCが存在すると考えて、それぞれ、sd(望ましい貯蓄率)、Cr(必要とされる投資率)という概念を導入し、それらが満たされ、しかも、社会全体でS=Iという財市場の均衡が実現されたときの成長率として「保証成長率(the warranted rate of growth)」Gwを提示した。
Gw=sd/Cr
これが、動学の基本方程式と呼ばれるもので、ハロッドは、このGwとGの大小関係で、各経済主体の行動パターンを整理した。Gw>Gの場合、sd>s、または、Cr<Cという関係が考えられ、家計は望んでいたよりも貯蓄が少ないので、より貯蓄を増やす(消費を削る)ように行動し、企業は、必要とされる投資よりも多く投資してしまったと感じ、投資額を削減しようと行動すると考えた。その結果、現実の成長率(G)は、益々、下がる傾向が強まり、GwとGの乖離はさらに広がると考えた。これが有名なハロッドの「不安定性の原理(Instability Principle)」である。
各経済主体が、計画を立てながら貯蓄や投資を行っていると考えると、このような乖離そのものが何故発生するのか疑問を感じる方もいると思われるが、企業が設備投資を行い、生産量を増加させたとしても、思ったよりも製品が売れずに在庫が増えたという状況は、よくある話である。固定資産のほかに在庫等の流動資産も経済学でいう「資本」の構成要素であるから、資本の増加分である投資も増加する。従って、「事後的に」Cr<Cであると企業が感じることはよくあることではないだろうか。家計の場合は、主に、所得が思ったよりも下がったり、予想しなかった支出が発生したりして、sd>sと判断することがあると思われる。
また、ハロッドは、たとえ、Gw=Gが実現されたとしても、社会全体が最適な状況とは限らないと考えた。これは、各企業や家計自らが望ましい生産活動(利益極大)や消費活動(効用極大)を行ったとしても、必ずしも完全雇用が実現されるとは限らないというケインズの考えに沿っている。社会全体が最適になるには、少なくとも、完全雇用が実現されてなければならない。人口の増加や技術革新を考慮に入れると、完全雇用が達成された場合に実現される成長率が存在すると考えられる。これが、ハロッドの「自然成長率(the natural rate of growth)」Gnで、政府は、経済政策を行ううえで、このGwをGnに近づける必要性があると説いた。ハロッドが1973年に出版した『経済動学』では、GとGwとGnの大小関係から、拡張主義的政策の影響とその是非が詳細に議論されている。
これらの経済動学の議論が「各国の経済政策に関する公理についての合意」になることをハロッド自身は望んでいたが、残念ながら、そのようにはならなかった。Gwの概念がなかなか他の経済学者に理解されなかったことと、GwやGnの実際的な測定の困難さが災いしていたような気がする。
保証成長率の概念の難しさ
米国のノーベル経済学賞受賞者のロバート・ソローは、1956年に公表した論文「経済成長理論への一寄与」の中で、ハロッドが展開した「不安定性原理」をGwとGn間のものと誤解した上に、さらに、ハロッドの議論が「資本係数(Cr)」の硬直性を前提としていると思い込み、Crの硬直性を排除した理論を組み立て、GwとGnが一致する可能性を例示し、ハロッドの「不安定性原理」は誤っていると特徴付けた。このことが、ハロッド理論の性格を決定付け、その後の経済学の教科書の記述内容を歪めてしまった。…
______
ソローはハロッドを矮小化した上で剽窃しただけだ。よくある話だ。
(ソローモデルはハロッドの図にそっくりだ。)
上記サイトはハロッドの哲学研究にも言及している。
______
経験の原理
ハロッドがこの「帰納法の妥当性」の証明として用意したのが、かれの言う「経験の原理(The Principle of Experience)」であるが、独創的な論証方法であったがために、専門的な哲学者から無視されることとなった。それは一体どのようなものだったのか。
かれは、この世の中には連続性があるという前提から議論を始める。「私たちが住んで来た世界が連続性を含んでおりませんでしたら、どんな方法を用いても、世界について何等の知識も得られなかったでしょう」と、かれの『社会科学とは何か』という書物の中で述べている。「連続性」というと分かりにくいが、要するに同じ事象が再現することで、あるAという前提のもとでBが発生するという個別の事象が何度も再現するところから、AならばBであるという一般的な法則、つまり知識を得ることができる訳で、このような事象の再現が全くない世界では、何等、知識は得られないとハロッドは考えている。
ハロッドは、このような、ある連続性を含む「連続体」を旅している旅行者の立場に立って議論を進めている。この旅行者はこの「連続体」がどこまで続くのか、どのような大きさなのか等について何の知識もない「完全に無知な人(Homo Ignorans)」であるという前提に立っている。この連続体の旅行は、遠い過去から連綿と続き将来へと伸びていく。
その最初の基点をA点とし、この旅行が終了する時点、つまり、連続性が途切れた時点をBとすると、AB線がこの旅行の全工程を示す。この旅行者は、このAB上のどこかの時点から旅行を開始し、この連続性が続くかどうかという質問を発していく。ハロッドは、このABを(X+1)等分に均等に分割し、その単位ごとに旅行者が「連続性が続いているか」との問いを発した場合に、正しい答えが返ってくる「確率」を問題にする。
図1、『帰納法論理の基礎』p.56より採録(但し、ABCDEFの記号は採録者が追記)
横軸のABと同じ長さの縦軸ACを引くと、ABCDの正方形が出来上がる。横軸は、質問の数、縦軸で過去から将来に渡って旅行者が確認をしてきた答えの数を表す。この旅行者が確認している現時点をP点とし、そこからABに平行して線を引き、対角線との交点をQとすると、PQは今までに連続性があったという正しい答えが返ってきた数を、QSは将来の答えの数を示す。この旅行に終わり、つまり、連続性が途切れるときがあるとすると、その場合に正しい答えが返ってくる確率は、X/(X+1)となる。
この旅行者が、連続体の旅行の中で、将来正しい答えを得る確率は、QS間で正しい答えを得る確率であるが、ハロッドは、この旅行者はQS(将来の答え)とQR(正しい将来の答え)の比率(QR/QS)も連続体そのものの長さも知ることができなので、これを確率に使うべきでないとして、△AEF÷△ADBの比率が求める確率となるべきだという。その値を計算すると、X2/(X+1)2となる。これが正しければ、連続体が経過する時間(X)が長ければ長いほど、その確率は高くなる。
ハロッドの議論はこのように、かなり込み入ってはいるが、要するに、ある事象が再現する頻度が高ければ高いほど、その確率は高くなるということで、ある意味では、常識的な結論ではないか思う。ハロッドはこのことを「連続体の確率逓増の法則(the law of increasing probability of continuance)」と呼び、これこそが「経験の原理」であると言う。この議論の中でハロッドは、この連続体の旅行の端にいる可能性は「ありそうもない(unlikely)」と考え、上記のXの値が限りなく大きな値となることを想定している。
かれは、①連続性がなければこの世の中の個別に事象から一般的な法則(知識)は得られない、②その連続性が持続する時間が長ければ長いほどその確率は高くなり信頼性は増す、③その意味で、帰納法の最も根本的な手続きは、表面的に一致する事例をもついくつかに事例を列挙して一般的な結論に導く「単純枚挙法(the method of simple enumeration)」であるとの結論に達した。
経験重視の経済学を求めて
生粋の経験主義者であったF.Y.エッジワースのもと、経験を重視した経済学を身につけたハロッドは、一貫して現実のさまざまな事象から丹念に思索を重ね、より一般的で普遍的な経済原理の樹立を求めてきた。そのひとつの例が「ハロッドの二分法」と呼ばれる提起ではなかったか。それは、まさに、上で言及した「帰納法」の手続きを「応用哲学」である経済学に適用してきたといっていい。
『経済動学』の最終章で、ハロッドは、今後、経済学者がなすべきこととして、以下のように述べている。
「まず第一に、われわれは経済動学の基本公理について、アルフレッド・マーシャルとパレートが定式化し、のちに「不完全競争」の理論によって修正をうけたミクロ静学の公理をお手本として、合意の成立をはかる必要があるということである。第二に、その公理から派生するものとして、各国の経済政策に関する公理について合意の成立をはかる必要があるということである。各種の政策を開始するにあたって公表された理論づけを見ると、現代経済動学の視点が全く欠落しているのが常だからである。第三に、そして最後に、われわれは、動学理論とその実践的応用とに関連する事実の流れを評価する方法を確立する必要があるということである。今日まで、最高の政策担当者によって示された政策の説明と理由づけは、非常に不十分なもののように思われる」
[参考文献]
1.Besomi, Daniele(ed.), The Collected Interwar Papers and Correspondence of Roy Harrod", 2003
2.Eltis, Walter, "Roy Harrod and the Keynesian revolution: his newly published correspondence", The European Journal of the History of Economic Thought, 2005
3.Harrod, Roy, "The Trade Cycle: An Essay", 1936(宮崎義一、浅野栄一訳『景気循環論』東洋経済新報社、1955年)
4.Harrod, Roy, "An Essay in Dynamic Theory", The Economic Journal, 1939
5.Harrod, Roy, "Memory", Mind, 51, 1942
6.Harrod, Roy, "Towards a Dynamic Economics", 1948(高橋長太郎、鈴木諒一訳『動態経済学序説』有斐閣、1953年)
7.Harrod, Roy, "Induction and Probability", Philosophy, 26, 1951
8.Harrod, Roy, "The Life of John Maynard Keynes", 1951(塩野谷九十九訳『ケインズ伝』東洋経済新報社、1954年)
9.Harrod, Roy, "Foundations of Inductive Logic", 1956
10.Harrod, Roy, "Towards a New Economic Policy", 1967(舘龍一郎監訳『新しい経済政策』竹内書店、1969年)
11.Harrod, Roy, "Sociology, Morals and Mystery",1972(清水幾太郎訳『社会科学とは何か』岩波新書、1975年)
12.Harrod, Roy, "Economic Dynamics", 1973(宮崎義一訳『経済動学』丸善、1976年)
13.伊東光晴『現代に生きるケインズ-モラル・サイエンスとしての経済理論-』岩波新書、2006年
14.Keynes, John Maynard, "A Treatise on Probability", 1921
15.Keynes, John Maynard, "Essays in Biography", 1933(熊谷尚夫、大野忠男訳『人物評伝』岩波書店、1959年)
16.Keynes, John Maynard, "The General Theory of Employment, Interest and Money", 1936(塩野谷九十九訳『雇用・利子および貨幣の一般理論』東洋経済新報社、1941年)
17.黒田東彦「『ある論争』で素顔をみたハロッド卿の思い出-インフレと不況の共存に新理論-」『エコノミスト』1991年9月10日号
18.Moggridge, Donald(ed.), "The Collected Writings of John Maynard Keynes Vol.XIV The General Theory and After", 1973
19.Rampa, Giorgio, Luciano Stella and A. P. Thirwall(ed.), "Economic Dynamics, Trade and Growth: Essays on Harrodian Themes", 1998
20.斎藤隆子「ハロッドの『経験の原理』と帰納法:ケインズの帰納法と比較して」『経済学史学会年報』第39号、2001年
21.Solow, Robert, "A Contribution to the Theory of Economic Growth", Quarterly Journal of Economics, 1956(福岡正夫、神谷伝造、川又邦雄訳『資本・成長・技術進歩』竹内書店、1970年)
22.Young, Warren, "Interpreting Mr Keynes - The IS-LM enigma", 1987(富田洋三、中島守善訳『IS-LMの謎-ケインズ経済学の解明』多賀出版、1994年)
23.Young, Warren and Frederic S. Lee, "Oxford Economics and Oxford Economists", 1993
ケインズ全集 第14巻 一般理論とその後―第II部 弁護と発展 | ジョン・メイナード・ケインズ, ドナルド・モグリッジ, 清水 啓典, 柿原 和夫, 細谷 圭 | 本 | Amazon.co.jp
http://www.amazon.co.jp/dp/4492813136商品の説明
内容紹介
本書(第14巻)の書名『一般理論とその後』は、第13巻(近刊)と共通である。第13巻は、その第I部、サブタイトルは「準備」であり、全5章からなる。これに対して、第14巻は第II部、サブタイトルは「弁護と発展」であり、全体の第6章「一般理論以後」を構成している。また、この巻には、『一般理論』の諸草稿と最終テキストの比較考証が付録として収録されている。
本巻は、そのサブタイトルが表しているように、『一般理論』刊行直後の1936年春から、その時代の主要な経済学者、すなわちホートリー、ロバートソン、ベヴァリッジ、ヒックス、ハロッドらとの間で、有効需要の原理、非自発的失業、資本の限界効率、流動性選好利子論、さらに経済統計と経済成長をめぐって議論を続けた論争の記録である。
とりわけケインズが説得に注力をしているのは『一般理論』の中核ともみなされる利子率の流動性選好理論で、最も多くの書簡がこの問題に関してやりとりされている。すなわちケインズは、将来に関する不確実な知識しかもたない人間の将来に対する不安の尺度として利子率を位置づけ、利子率理論を通じて、将来予想が経済活動に与える影響を経済分析に導入したのである。
最近では、前例のない世界的な金融緩和にもかかわらずデフレ傾向が続き、利子率が低水準に定着する状態が長期化している。これらの現象の解明には、ケインズが本書で詳しく説明している流動性選好理論を再検討することが重要なヒントになる可能性が含まれている。
2016年は、『一般理論』刊行後80年、ケインズ没後70年の年である。改めてケインズ理論の再検討、再評価が望まれる。
著者について
ジョン・メイナード・ケインズ(ジョン メイナード ケインズ)
ドナルド・モグリッジ(ドナルド モグリッジ)
清水 啓典(シミズ ヨシノリ)
一橋大学名誉教授
細谷 圭(ホソヤ ケイ)
東北学院大学准教授
登録情報
単行本: 676ページ
出版社: 東洋経済新報社 (2016/1/15)
言語: 日本語
ISBN-10: 4492813136
ISBN-13: 978-4492813133
本巻は、そのサブタイトルが表しているように、『一般理論』刊行直後の1936年春から、その時代の主要な経済学者、すなわちホートリー、ロバートソン、ベヴァリッジ、ヒックス、ハロッドらとの間で、有効需要の原理、非自発的失業、資本の限界効率、流動性選好利子論、さらに経済統計と経済成長をめぐって議論を続けた論争の記録である。
とりわけケインズが説得に注力をしているのは『一般理論』の中核ともみなされる利子率の流動性選好理論で、最も多くの書簡がこの問題に関してやりとりされている。すなわちケインズは、将来に関する不確実な知識しかもたない人間の将来に対する不安の尺度として利子率を位置づけ、利子率理論を通じて、将来予想が経済活動に与える影響を経済分析に導入したのである。
最近では、前例のない世界的な金融緩和にもかかわらずデフレ傾向が続き、利子率が低水準に定着する状態が長期化している。これらの現象の解明には、ケインズが本書で詳しく説明している流動性選好理論を再検討することが重要なヒントになる可能性が含まれている。
2016年は、『一般理論』刊行後80年、ケインズ没後70年の年である。改めてケインズ理論の再検討、再評価が望まれる。
著者について
ジョン・メイナード・ケインズ(ジョン メイナード ケインズ)
ドナルド・モグリッジ(ドナルド モグリッジ)
清水 啓典(シミズ ヨシノリ)
一橋大学名誉教授
細谷 圭(ホソヤ ケイ)
東北学院大学准教授
登録情報
単行本: 676ページ
出版社: 東洋経済新報社 (2016/1/15)
言語: 日本語
ISBN-10: 4492813136
ISBN-13: 978-4492813133
ロイ・F・ハロッド卿 (Sir Roy F. Harrod, 1900-1978)
http://cruel.org/econthought/profiles/harrod.html
ロイ・ハロッドは1924年から1967年の引退まで、オックスフォード大学で経済学を教え、独自の貢献を行ってきた。1922 年にオックスフォード大クライストチャーチで講師に選ばれてから、ケンブリッジ大学で数ヶ月ほど J.M. ケインズと過ごし、その後もケインズとは親密なつきあいを続け、1951年には公式のケインズ伝を発表している。
ヒックスやミード と共に、ハロッドはケインズ一味に加わったオックスフォードの経済学者の一人だった。ヒューバート・ヘンダーソンとオックスフォード経済研究グループを創設した彼は、経済問題に対して「静的」より「動的」なアプローチを推奨したが、これはオックスフォード大の貢献と見なされ、ケンブリッジ派経済学者に受け入れられたのは後になってからだった。
ハロッド独自の「限界収入曲線」の論文を当時のEconomic Journal編集者だったケインズが二年 (1928 から 1930) 遅らせたために、このオックスフォード経済学者はこの分野の第一人者とは見なされなくなってしまった。こうした悲しいめぐりあわせはハロッドの傷害で何度 か繰り返されたた。ハロッドは独立に短期平均費用曲線の長期的包絡線を実質的に発見した (1931) が、これも認知されなかった――これは ヴァイナーの発見とされたのだった。この同じ論文で、彼は不完全競争の分析基盤をかためている――だがその栄誉を手に入れたのはジョーン・ロビンソンだった。著書Trade Cycle (1936) で発展させた見事な乗数アクセラレータモデルの栄冠は、それを数学的に表現した サミュエルソン と ヒックスに渡った。IS-LM モデル の方程式を記述したのはハロッド (1937) だったが、先駆者としての座は後にそれを図に描いたヒックスが持っていってしまった。1939 年の起業家行動に関する論文――利潤最大化行動に自然淘汰または「進化的」メカニズムがあるという記述を行った最初期のもの――はほとんど無視され、後に アルチアン(1950) がそれを提案することになる。
やっと彼の名前が多少は知れ渡った発見が、ハロッド (1939) 「動的理論に関するエッセイ」だった。この発想は現代 成長理論の嚆矢であり、エヴセイ・ドーマーが追従したが、今度こそハロッドの名前もモデルに残った。それが「ハロッド=ドーマーモデル」だ。1948 年の著書Towards a Dynamic Economicsおよび一連の論文 (1960, 1963, 1975) で、彼はこれをさらに進め、モデルの不安定性問題に光を当てて、経済成長に関する戦後研究すべての出発点となった――そしてさらには景気循環論(ビジネスサイクル理論) も復活させた。
国際貿易 (1933, 1958) および不完全競争 (1933, 1934, 1952) についての貢献も認められたのは後になってからだった。あまり厳密ではないが経済政策に関する論文 (1963, 1965, 1968, 1969) も見事なものだ。1952年にはオックスフォードのナットフィールド大経済学Readerに任命され、同大学の応用経済学フェローシップで記念されてい る。
経済理論以外で、ハロッドは帰納論理に関する研究 (1956)、第二次大戦中の統計スタッフおよびウィンストン・チャーチルへの個人顧問、さらにハロルド・マクミラン首相への非公式アドバイスで有名だ。またオックスフォードカレッジにかなりのエネルギーを割いている。
____
経済学は論理学、そしてモラル・サイエンス ( 景気 ) - 平井俊顕 (ひらい・としあきToshiaki Hirai)ブログ - Yahoo!ブログ
http://blogs.yahoo.co.jp/olympass/49280998.html経済学は論理学、そしてモラル・サイエンス
経済学は論理学の一分野であり、思考の一方法です。……経済学は本質的にモラル・サイエンスであって自然科学ではありません(ハロッド宛書簡、一九三八年七月四日付。JMK. 14, pp. 296-7)。
これは計量経済学の先駆的業績であるヤン・ティンバーゲン(Tinbergen[1939])をめぐり、ケインズとハロッドのあいだで交わされた書簡の一節である。ティンバーゲンに対するケインズの評価は徹頭徹尾、厳しいものであった。その際、ケインズは自らの経済学に対するスタンスを次の二点におく。一つは、経済学を論理学の一分野とみなすスタンスである。経済学はモデルの改善によって進歩するが、可変的な関数に実際の数値を当てはめるべきではない。統計的研究の目的は、モデルのレリヴァンス・有効性をテストすることにある。この背後には『確率論』(JMK. 2)で展開した理論が確実に存在する。だがケインズの経済学が、計量経済学および一般均衡論の発展と連携してマクロ経済学の主流となったのは皮肉である。もう一つは、経済学をモラル・サイエンスと特徴づけるスタンスである。これは、内省と価値判断を用い、動機、期待、心理的不確実性を扱う科学と定義されている。「新しい古典派」のような「形式主義」と真っ向から対立する方法論である。







9 Comments:
CONTENTS
1. THE HUMAN FACTOR
(i) Preliminary
(ii) The Division of Labour
(iii) Capitalism
(iv) The Monetary System
II. INVESTMENT AND OUTPUT
(i) The Relation
(ii) The Multiplier
(iii) The Movements of Prices and Profits
(iv) The Three Dynamic Determinants
(v) The Inevitability of the Cycle
Note on Saving
III. INTEREST, MONEY, AND THE FOREIGN BALANCE
(i) The Rate of Interest
(ii ) Money
(iii) The Foreign Balance
IV. THE QUESTION OF REMEDIES
(i) Remedy and Diagnosis
(ii) Stable Money
(iii) Public Works and Public Finance
(iv) Subsidies
INDEX
The Trade Cycle, An Essay(1936):
http://dl.ndl.go.jp/info:ndljp/pid/3020415
景気循環論
著者 R.F.ハロッド 著[他]
出版者 東洋経済新報社
出版年月日 1963(1955とほぼ同じ。中公は1、2章のみ)
目次
序文
日本版への序
凡例
第一章 人間的要因/p1
I 予備的考察/p1
II 分業/p14
III 資本主義/p27
IV 貨幣制度/p40
第二章 投資と産出量/p60
I リレーション/p60
II 乗数/p72
III 物価と利潤の動き/p83
IV 三つの動学的決定要因/p97
V 景気循環の不可避性/p112
補論 貯蓄にかんする覚え書/p118
第三章 利子・貨幣および国際収支/p123
I 利子率/p123
II 貨幣/p141
III 国際収支/p163
第四章 治療の問題/p178
I 治療と診断/p178
II 安定貨幣/p193
III 公共事業と財政/p214
IV 補助金/p251
訳者注/p261
訳者あとがき/p271
事項索引/p0
人名索引/p0
引用書名索引/p0
_________
http://homepage1.nifty.com/gujyo-economic-res/macro.files/harodo.htm
マンキューの「マクロ経済学」では、経済成長を語るために、新古典派のソローモデルを使っています。どうしてソローモデルなのか?それは、以前まではケインズ経済学の流れを汲むハロッド=ドーマー・モデルが主流でしたが、1950年代から1960年代には既に、新古典派経済学による経済成長理論がその中心的存在になっていました、そして、現在は、長い間のアメリカ経済の長期低迷とその後のIT革命等によるアメリカ経済の空前の長期的な好景気が手伝って、内生的成長理論が注目されるようになっています。
なぜ、ケインズ経済学の流れを汲むハロッド=ドーマー・モデルが注目されないのかというと、価格の硬直性が前提になっており、完全雇用は達成されず、経済成長も不安定になるという結論しか導かれていないからです。
確かに、ハロッド=ドーマー・モデルにおいては、「ナイフ・エッジ定理」と呼ばれるように、短期不安定性と長期不安定性が存在します。
まず、ハロッド・モデルについて説明すると、ハロッドは3つの成長率を想定しています。それは①現実成長率G、②適正成長率(保証成長率)Gw、③自然成長率Gnの3つです。
①現実成長率Gは、国民所得の決定の理論の出発点であるI=Sという投資と貯蓄が等しいということから導き出されます。産出量をY、その増分をΔYとして、両辺をYで割ると、
I=S
I/Y=S/Y
更に、両辺にΔY/Δ=1を掛けると ΔY/Y×I/ΔY=S/Y・・・①
ここで、 ΔY/Y=Gなので、 G×I/ΔY=S/Y
よって、 G=ΔY/I×S/Y
G=ΔY/Y
となります。
ここで、①式に戻るとS/Yは平均貯蓄率であり、I/ΔYはI=ΔKという「投資は資本ストックの増加分である」という仮定で変形すると、I/ΔY=ΔK/ΔYで、ハロッドは資本係数と呼んでいます。特に、現実の国民所得の増加分で、現実の資本ストックの増加分を割った値であるため現実資本係数と言います。
S/Y=s、ΔK/ΔY=Cとすれば、GC=s・・・②というハロッドの基本方程式が得られます。
次に、②適正成長率(保証成長率)Gwは、企業家の合理的行動を満足させ、資本設備の完全利用が実現される時に達成される企業均衡の生産成長率です。上記②のハロッドの基本方程式は、GwCr=s・・・③と変形されます。ここでの、Crは国民所得を1単位増加させるために生産技術にまさに必要とされる資本量の増加比率のことで、必要資本係数と呼ばれます。また、ここでのsは、②の基本方程式で得られる貯蓄率とは別物で、計画された貯蓄で、すべて実現されるという仮定の概念であることから、事後的貯蓄率に相当します。
なお、必要資本係数の考え方の根底には、投資決定理論として加速度原理が働くので、
投資関数を独立投資を無視して、誘発投資のみと仮定すれば、
誘発投資をIt =v(Yt-1-Yt-2)、貯蓄をSt=s・Yt-1とすれば、
I=Sより、 It =St
v(Yt-1-Yt-2)=s・Yt-1
s= v(Yt-1-Yt-2)/Yt-1
(Yt-1-Yt-2)/Yt-1=s/v
ここで、Yt-1-Yt-2=ΔY、Yt-1 =Yと置けば、
誘発投資はI=vΔY、v=It/ΔY=I/ΔYなので、vは必要資本係数Crと同じであることがわかります。
最後に、③自然成長率Gnは、完全雇用を持続し、しかも年々の技術進歩による労働生産性の上昇分を吸収したときに、達成できる最大可能な国民生産物の成長率をいいます。
ここで、ハロッドは労働の需要と供給の均衡に注目し、労働需要をL=l・Yとし、
l=L/Yを雇用係数と考えました。いま、労働人口が年々n%の割合で増加するものと仮定すると、労働人口の増加は、ΔL=nLとなり、右辺に労働需要(L=l・Y)を代入すると ΔL=n・l・Yとなり、
両辺をl・Yで割ると、 n=ΔL/l・Y=ΔL/L となります。
ここで、労働需要の増加分を考えると、ΔL=l・ΔYより、
l=ΔL/ΔY
ΔL=n・(ΔL/ΔY)・Y
ΔL=(n・ΔL・Y)/ΔY
両辺にΔYを掛けると n・ΔL・Y=ΔL・ΔY
nY=ΔY
n=ΔY/Y
ここで、ΔY/Y=Gnとすれば、Gn=n・・・④となります。
しかしながら、現実のデータでは高度成長期に、資本係数がほぼ3で、貯蓄率が30%位であることから、3Gw=30、よりGw=10%であり、ほぼG=Gwと考えても良さそうですが、労働人口の増加率も1%前後あり、Gn=Gwが成立しません。
そこで、労働生産性の向上、つまり技術進歩率の概念を導入して、これをλとして変形すると、④式より Gn=n+λ・・・⑤となります。
これまでのハロッド・モデルについてまとめると、以下のとおりです。 次に、ハロッドの3つの成長率の比較検討の考え方ですが、短期分析と長期分析の2種類あります。
まず、短期分析においては、現実成長率と保証成長率が乖離してしまうとどのようになるのか?ということに注目します。
最初に、現実成長率の基本方程式GC=sと保証成長率の基本方程式GwCr=sにおいて、貯蓄率がどちらもsなので、区別化するために現実成長率の貯蓄率Spを事後的貯蓄率、保証成長率の貯蓄率Saを事前的な貯蓄率とすると、それぞれ基本方程式は次のようになります。
現実成長率G=Sp/C、保証成長率Gw=Sa/Cr
まず、(A)として、現実成長率が保証成長率から上方へ乖離する場合を考えると、
G>Gwであるから、 Sp/C>Sa/Crであることから、2つのケースが考えられます。(下記の図を参照)
a)Sp=Saであれば、C<Crとなり、現実資本係数が必要資本係数よりも小さい ので、需要が活発で、生産増が求められます。現実資本ストックの不足分を純投資の 増加分で埋め合わせると、乗数理論により現実成長率はますます拡大するという不安 定な状態になります。
b)C=Crであれば、 Sp>Saとなり、実際の貯蓄率(事後的貯蓄率)が意図さ れた貯蓄率(事前的貯蓄率)を上回るので、予想よりも消費支出額が少なかったこと であり、消費財需要が予想外に低かったことを意味します。よって、次期以降も高貯 蓄が続くならば、消費支出がさらに増大して、加速度原理を媒介して誘発投資が招来 され、所得増加を引き起こします。 図1 ハロッド・モデルの短期不安定性
次に、(B)として現実成長率が保証成長率から下方へ乖離する場合を考えると、
G<Gwであるから、 Sp/C<Sa/Crであることから、2つのケースが考えられます。(上記の図を参照)
a)Sp=Saであれば、C>Crなので、現実資本係数が必要資本係数を上回るの で、資本の食いつぶし、すなわち負の純投資が行われるので、次期の純投資が減少 し、ますます現実の成長率は下方へ乖離していきます。
b)C=Crであれば、Sp<Saなので、現実の貯蓄率が計画された貯蓄率を下回 るために、消費の減少から加速度原理により、負の誘発投資が行われ、所得水準が ますます下方へ乖離していきます。
このように、短期においては、現実成長率が保証成長率が非常に不安定な軌道上にあることが証明されたわけです。
次に、長期分析ですが自然成長率Gnと保証成長率Gwの乖離する場合に着目して、短期変動モデルである現実成長率Gと保証成長率Gwの乖離を長期モデルに組み入れて分析します。
まず、自然成長率Gnの成長軌道は完全雇用天井成長線なので、保証成長率Gwの軌道の上方に位置させることができます。
ある期に G>Gwという現実成長率が保証成長率から上方へ乖離する場合を考えると、図2のGn軌道<Gw軌道と仮定した場合で見る限り、現実経済がやがてGn成長軌道に衝突し、現実成長率Gが(a)の矢印のごとく下方に反転するか、(b)の矢印のごとくGn軌道に沿って進むかの2通りが考えられます。
図2 Gn軌道<Gw軌道となっている場合
最初に、Gn軌道<Gw軌道となっている場合を考えると、あくまでもGn軌道がGw軌道よりも小さいとは、Gn軌道の傾きが、Gw軌道の傾きよりも小さいという意味であり、Gnの国民所得水準が、Gwの国民所得水準を下回ってしまうということを意味していません。あくまでも経済成長「率」が小さいということなので留意してください。
さて、Gn<Gwであるのならば、G<Gwの関係が成り立つので、図2の(b)の矢印のように進み続けることはできません。よって現実の経済は下向きに反転し、経済は長期停滞状態に陥っていることになります。Gn<Gwにおいて、Gnは人口成長率、Gwは資本蓄積率を示しているので、Crを必要資本係数、Saを事前的な貯蓄率とすると、 GnCr<GwCr=Sa
と変形することができて、 GnCr<Sa となるので、GnCrは完全雇用水準での必要な投資率を意味し、投資率が貯蓄率を下回ることを意味します。
したがって、Gn<Gwは資本蓄積率が人口成長率を上回る先進諸国にみられる典型的な事例であり、この不等式関係は有効需要の不足から生じます。そこで生じる失業は有効需要不足から発生するので、ケインズ的失業が発生していると言われます。
次に、Gn軌道>Gw軌道となっている場合を考えると、Gn軌道の傾きが、Gw軌道の傾きよりも大きいので、図3のようになります。
図3 Gn軌道>Gw軌道となっている場合
さて、Gn>Gwであるのならば、G>Gwの関係が成り立つので、現実成長率Gは、完全雇用天井成長軌道に向かって図3の(a)の矢印のように進むことになります。ところが、GはGnを飛び越えて進むことができないので、持続的インフレーション傾向になります。
しかしながら、Gnはとめどなく完全雇用天井成長軌道に沿って上昇するのではなくて、
Gn>Gwなので、
GnCr>GwCr=Sa
の関係が成立するので、GnCr>Saとなり、人口成長率が資本蓄積率を上回り、慢性的に豊富な有効需要にこたえるだけの資本蓄積が不足しているために、図3の(b)のようにGは下方へ反転せざるをえません。このケースは発展途上国に典型的に見られるケースでジョン・ロビンソンによれば、ここで発生する失業をマルクス的失業と呼んでいます。 このように、ハロッド・モデルでは、G=Gw=Gnの均衡成長(ゴールデン・エイジ)を持続することを保証しえず、それは「かみそりの刃」の上を渡るほど不安定このうえないことからナイフエッジ定理とも呼ばれている訳です。
参考文献「現代経済学」(石橋春男著・成文堂・1993年)
http://homepage1.nifty.com/gujyo-economic-res/macro.files/me0101.jpg
http://homepage1.nifty.com/gujyo-economic-res/macro.files/me0102.jpg
http://homepage1.nifty.com/gujyo-economic-res/macro.files/me0103.jpg
http://homepage1.nifty.com/gujyo-economic-res/macro.files/me0104.jpg
ハロッド動学のアンティノミー理論は なぜ失われたのか? 中 村 ... - J-Stage (Adobe PDF)
www.jstage.jst.go.jp/article/jshet1963/41/41/41.../_pdf
いて, 乗数 とリレーション(加速度原理)の 相互. 関連 によって景気循環を解明する先駆 的な試み. を提示した. 乗数 と加速度の結合は, その後の. 経済変動論(景 気循環論 と 経済成長論)に 大 き. く影響を与 えた重要な業績である. しかしその. こと以上に, ハロッド ...
経済学者ハロッド
www2.gol.com/users/nojiri/harrod.html
ケインズの『一般理論』の出版の直後(1936年、『一般理論』と同年に出版)に刊行され た、ハロッドの『景気循環論』で、ハロッドは初めて乗数と加速度因子(ハロッド自らは「 リレーション」と呼んでいた)の相互作用による景気循環理論を提唱したが、この「乗数」 の ...
カレツキはハロッドの加速度原理を批判したらしいが、、、
ハロッドの「投資の生産力効果」と「適正成長率」Author(s)居城, 舜子
http://eprints.lib.hokudai.ac.jp/dspace/bitstream/2115/31409/1/28%281%29_P139-169.pdf
ブルス148頁
《カレツキが「黄金律」的解決の発見に注意を集中しなかったのは、それが彼にとっては、技術進歩の型にかんする若干の仮定のもとでは、効果的なヴァリアントの上限を示すことができるだけだからであった。彼はこういっている。「資本集約度の選択における枢要問題は、鍛え直しの過程における生活水準の問題である☆」と「鍛え直し」とは、資本集約度のより低い水準からより高い水準ヘの、資本設備の漸次的転換をさす)。『社会主義経済成長論概要』の該当する章の注意ぶかい読者ならば、このばあいには成長率(およびそれに対応するすべてのパラメーター)がある水準から他の水準に切り換えられるのは、ある転換点においてだけのことではなく、事実上、移行期の全期間をつうじて変化が進行するのだ、という点にも気づくことであろう。カレツキがなぜ、彼のアプローチを伝統的な成長論のそれと対比させ、「異なった社会体制における成長論」にかんする論文のなかで、「長期経済成長についての下らぬ著作の大部分は、『比較静態学』の次元で書かれている」と言明している理由は、なによりもこのことによって説明される。》
☆(竹浪祥一郎訳『社会主義経済成長論概要』日本評論社、 一九六五年)
Kalecki, M., (1972), Selected Essays on the Economic Growth of the Socialist and the Mixed. Economy, Cambridge.
69頁
ハロッド=ドーマー・モデル(英語表記)Harrod-Domar Model
ブリタニカ国際大百科事典 小項目事典の解説
ハロッド=ドーマー・モデル
Harrod-Domar Model
J.M.ケインズが『一般理論』で示した完全雇用均衡のモデルを動学化したものであり,R.F.ハロッドと E.D.ドーマーによりほぼ同時期に開発された。この特徴は,新古典派のモデルと違い,生産要素を代替的でなく補完的に見るところにある。ある生産活動に振り向けられる資本と労働の関係を固定的であるとする。したがってこのモデルは,労働供給に制約がないとともに,資本係数が固定的である生産関係が前提になっている。そしてこのモデルにおいて,成長率は貯蓄率を (限界) 資本係数で割ったものとして定義される。この成長率を維持し続けることはきわめて不安定であるということも一つの特徴である。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
コメントを投稿
<< Home