グラフ理論（ケーニヒスベルクの橋）関連：メモ

グラフ理論①(一筆書きの定理)

https://youtu.be/PFcuUpBwgtE

グラフ理論②(オイラーの多面体定理)

https://youtu.be/8ko9EAVeg4U

　　　　　　　　　　　　　　　　　（リンク:::::::::、数学、論理学）

グラフ理論（ケーニヒスベルクの橋）関連：メモ

http://nam-students.blogspot.jp/2016/03/blog-post_11.html（本頁）

◎〇20160310 AlphaGo◉ div style="line-height: 9pt;"

http://nam-students.blogspot.jp/2016/03/20160310-alphago.html

　／Ｉ＼

／　Ｉ　＼

＼　Ｉ　　＼

　＼Ｉ＿＿＿＼

　／Ｉ　　　／

／　Ｉ　　／

＼　Ｉ　／

　＼Ｉ／

グラフ理論からネットワーク理論へ

エルデシュ数（エルデシュすう、Erdős number）またはエルデシュ番号とは、数学者同士、あるいはもっと広く科学者同士の、共著論文による結び付きにおいて、ハンガリー出身の数学者ポール・エルデシュとどれだけ近いかを表す概念である。エルデシュに共著論文が非常に多いことから、その友人たちによって、敬意とユーモアを込めて考え出された。今日では科学者のコミュニティにおいてよく知られており、エルデシュと近いことが名誉であるかのように半ば冗談めいて語られる。

一筆書き - Wikipedia

https://ja.m.wikipedia.org/wiki/%E4%B8%80%E7%AD%86%E6%9B%B8%E3%81%8D

問題編集

18世紀の初めごろにプロイセン王国の首都であるケーニヒスベルク（現ロシア連邦カリーニングラード）という大きな町があった。この町の中央には、プレーゲル川という大きな川が流れており、七つの橋が架けられていた。あるとき町の人が、次のように言った。

「このプレーゲル川に架かっている7つの橋を2度通らずに、全て渡って、元の所に帰ってくることができるか。ただし、どこから出発してもよい」

町の人が言ったことはできるだろうか。

グラフ理論との関連編集

1736年、レオンハルト・オイラーは、この問題を以下のグラフに置き換えて考えた。

 → 

このグラフが一筆書き可能であれば、ケーニヒスベルクの橋を全て1度ずつ通って戻ってくるルートが存在することになる。

そして、オイラーは、このグラフが一筆書きできないことを証明し、ケーニヒスベルクの問題を否定的に解決した。

この問題は論理的に考えれば確かに不可能であるが、実は屁理屈気味だが解法が存在している。それは、「川の源流まで辿る、という大きな迂回ルートを通る」ことで経路を一本増やすことができ、解答可能になる。これは問題の文章には一切違反していないので正当な回答とみなせなくもないが、いわゆる「題意」からは外れる。

一筆書き可能かどうかの判定法編集

ある連結グラフが一筆書き可能な場合の必要十分条件は、以下の条件のいずれか一方が成り立つことである（オイラー路参照）。

• すべての頂点の次数（頂点につながっている辺の数）が偶数 →運筆が起点に戻る場合（閉路）
• 次数が奇数である頂点の数が2で、残りの頂点の次数は全て偶数　→運筆が起点に戻らない場合（閉路でない路）

一筆書きの解法編集

• すべての頂点の次数が偶数 →ある頂点から出発し、元の頂点に戻り、さらにその頂点から出発し、元の頂点に戻る順路を考える。もし、まだ通っていない経路があれば、先ほどの順路からある頂点を選び、そこから寄り道をしてその頂点に戻ってくる順路を付け足したものに修正する。その修正を繰り返せばよい。
• 次数が奇数の頂点の数が2で、残りの頂点の次数は全て偶数 →ある奇点から出発し、もう一方の奇点へ抜ける順路を考える。もし、まだ通っていない経路があれば、先ほどの順路からある頂点を選び、そこから寄り道をしてその頂点に戻ってくる順路を付け足したものに修正する。その修正を繰り返せばよい。

グラフ理論 - Wikipedia

https://ja.wikipedia.org/wiki/%E3%82%B0%E3%83%A9%E3%83%95%E7%90%86%E8%AB%96

グラフ理論（グラフりろん、英: graph theory）は、ノード（節点^{[英 1]}・頂点^{[英 2]}）の集合とエッジ（枝・辺^{[英 3]}）の集合で構成されるグラフ^{[英 4]}に関する数学の理論である。グラフ (データ構造) などの応用がある。

グラフ理論の基礎 | 高校数学の美しい物語

http://mathtrain.jp/graph

グラフ理論は組み合わせの問題を簡潔に記述するための道具です。

グラフとは

・グラフとは，点の集合 V$V$ と二点間を結ぶ辺 E$E$ の集合のペアで，G=(V,E)$GVE$ と表します。点のことを頂点，ノード(vertex,node)，辺のことを枝(arc,edge)などと呼びます。

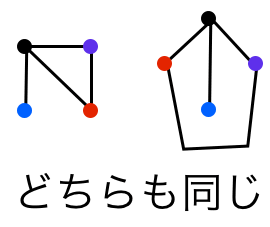
• グラフは組み合わせ的な構造を表すモデルです。そのため，図における二つのグラフは同じモデルとみなします。頂点の置き方やどのような曲線で結ばれているかは考えません（図では分かりやすくするために頂点に色をつけています）。
• 辺に方向性があるようなグラフを有向グラフ，方向性がないようなものを無向グラフと呼びます。図は無向グラフです，有向グラフでは辺を矢印で表します。問題によって使い分けましょう。

グラフ理論と数学オリンピック

数学オリンピックではグラフ理論を使うとスッキリと記述できる問題が多く出題されています。これらの問題はグラフ理論を全く知らなくても解けるようになっており．グラフ理論の難しい定理を知っていて有利になる場面は少ないです。

しかし，グラフ理論を知っていると問題を簡潔な言葉で記述することができ，見通しがよくなります。「人間」とか「知り合い」などの日本語で議論するよりもグラフを描いて頂点と辺で議論した方が圧倒的に分かりやすいのです。

そのような意味で，最低限のグラフ理論の概念と用語を知っていると数学オリンピックでは有利です。

例

• 2001JMO本選問1：握手の補題とエルデシュガライの定理
• 2014JJMO本選問4：2014年JJMO本選第4問の解説
• 1992IMO問3：ラムゼーの定理と6人の問題

他にもいくらでもあります！

グラフ理論で重要な用語

感覚的にはごく自然な用語たちです。いろいろな概念を簡潔に表現することができるので便利です。

• （頂点の）次数：頂点から出ている辺の本数。
• 連結：どの頂点からどの頂点へも辺を伝っていくことができるようなグラフ。
• パス（道）：隣接する頂点をたどったもの。ただし，「同じ頂点を二回通るのはダメ」とすることが多い。
• サイクル（閉路）：隣接する頂点をたどったもので，始点と終点が同じもの。ただし，同じ辺を二回通るのはダメ。

重要なグラフ

数学オリンピックの問題でもしばしば登場するグラフたちです。

・木：閉路が存在しない連結なグラフ。

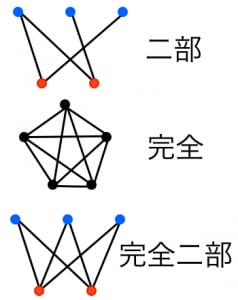
• 二部グラフ：頂点が二つのグループに分かれており，異なるグループの頂点間にのみ辺が引かれているグラフ。
• 完全グラフ：全ての頂点間に辺が引かれているグラフ。頂点数 n$n$ の完全グラフを Kn$K_n$ と書く（図は K5$K_5$）。
• 完全二部グラフ：二部グラフで，異なるグループの頂点間には全て辺が引かれているグラフ。グループの頂点数がそれぞれ m,n$mn$ である完全二部グラフを Km,n$K_{mn}$ と書く（図は K3,2$K_{32}$）。

・オイラーグラフ：一筆書きできるグラフ。
→オイラーグラフの定理とその証明