ちなみに、ドゥルーズの『アンチ・オイディプス』におけるベルグソンの思想の要約では、全体と生命が、開かれているが故に相似形だということになっている。
ミンコフスキー図やそれをひっくり返したペンローズ図など、視覚的な図式が(それを固定した概念ではなく述語という動詞として活用する限りで)高度な概念を理解する上で有効なものとしてあるが、フラクタルに関しては複素平面(複素数平面、ガウス平面ともいわれる)が1から2次元の立体?を平面に移す際のフォーマットとしてフラクタルCGに欠かせないものになっている。
興味深い事例として、マンデルブロは、株価相場も自己相似形だといっているが、これは10円投資するひとの100円と10万円投資するひとの100万円とが相対的に同じ価値であり、同じ決断の仕方を取ることから説明できる(『フラクタル』高安秀樹、朝倉書店)。
さて、フラクタルが僕に取って魅力的なのは自然環境の自己成長作用における原理として活用できるからであるのも無論だが、組織原理に応用できるからだ。
柄谷行人が言うように、アソシエーションを4象限の図で説明できるとして(参考図1)、アソシエーションの内部もまた4象限に分割できるというのが僕の意見だ(参考図2)。ここでフラクタルの自己相似性という概念が役に立つ。
図1
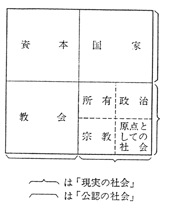
(上記の図を以下のような黄金数を活用した自己相似形と同様のものとして考えることができる。指数ではなく対数に比例する対数らせんを想定する。正方形のままフラクタルを製図すればよかったが。↓)
図2
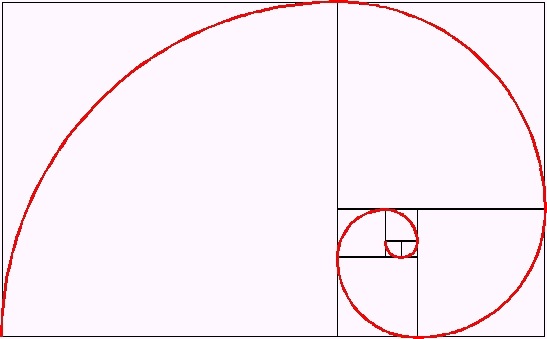
組織原理を感覚ではなく数式で説明出来るし、立体的に図で説明することも出来るだろう。立体にする場合には、細かい部分ほど頂点が高く鋭い山になると考えることができる。これは小さいからといって費やすエネルギーを節約するなという教訓にもなるし、ミクロからマクロの波及効果も説明できる。(参考図3、4)
図3

(この図は以下のように考えられる↓。)
図4
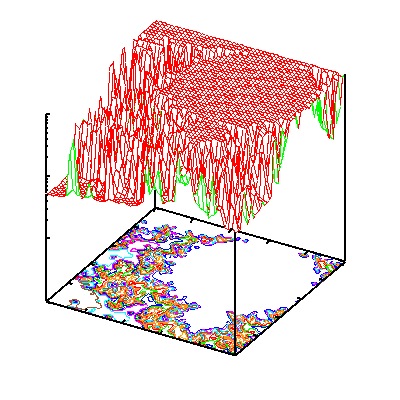
年金問題にしても、地方の窓口の情報が自己相似形を保ったまま中央のデータベースとつながっていればよかったと思うが、当時の役人や政治家にそうした発想は難しかったかもしれない。
カント(**)なら目的なき合目的性と呼ぶかもしれないが、統制的理念として自然成長性を説明するフラクタル(黄金比やフィボナッチ数列などの連分数も概念的に含む)の重要性は増しており、何より一般的になりつつある(***)。
肝心の、相似系をなす最初の自己がそれ自身で多元性を持つべきだとも思うが、そうした視点をもたらす離散数学ともフラクタルは相性がいいと思う
*『フラクタル幾何学』(日経サイエンス)
**ポプラの枝を切らせて教会の尖塔を見たがったカントは、フラクタルの概念をどう思っただろうか。
***最近だと北野武監督「takeshis’」の原題が『フラクタル』だったが、残念ながら改題されてしまった。
参考サイト:
http://t16web.lanl.gov/Kawano/gnuplot/fractal/mandelbrot.html
日経サイエンス1999.5
フラクタル島の形成 アニメーション
https://youtu.be/A5OqzsB1F-k

━━━━━━┓
┃
┃
┃
┃
┃
━━━━━━┛
┏━━━━┓
┃ ┃ ┃
┗━┛ ┏━┛
┃
┏━┓ ┗━┓
┃ ┃ ┃
┗━━━━┛
┓┏━┓┏━┓
┏┛┗┓┗┛┏┛
┃┏┓┃┏┓┗┓
┗┛┗┛┃┗━┛
┏┓┏┓┃┏━┓
┃┗┛┃┗┛┏┛
┗┓┏┛┏┓┗┓
┛┗━┛┗━┛
上の図はペアノ(Peano)曲線と呼ばれるもので、最初の単純な曲線を半分に縮小し、向きを変えて4枚貼り合わせます。
次に線で結びます。これを繰り返すとどんどん複雑になって無限に繰り返すと正方形を埋め尽くします。
自己相似形の繰り返しという意味でフラクタルになっています。
http://homepage3.nifty.com/SGL/FRACTAL/
┏━┓┏━┓┏━┓┏━┓┏━┓
┗┛┏┛┗┓┗┛┏┛┗┓┗┛┏┛
┏┓┗┓┏┛┏┓┃┏┓┃┏┓┗┓
┃┗━┛┗━┛┃┗┛┗┛┃┗━┛
┗┓┏━━┓┏┛┏┓┏┓┃┏━┓
┏┛┗┓┏┛┗┓┃┗┛┃┗┛┏┛
┃┏┓┃┃┏┓┃┗┓┏┛┏┓┗┓
┗┛┗┛┗┛┗┛┏┛┗━┛┗━┛
┏┓┏┓┏┓┏┓┗┓┏━┓┏━┓
┃┗┛┃┃┗┛┃┏┛┗┓┗┛┏┛
┗┓┏┛┗┓┏┛┃┏┓┃┏┓┗┓
┏┛┗━━┛┗┓┗┛┗┛┃┗━┛
┃┏━┓┏━┓┃┏┓┏┓┃┏━┓
┗┛┏┛┗┓┗┛┃┗┛┃┗┛┏┛
┏┓┗┓┏┛┏┓┗┓┏┛┏┓┗┓
┗━┛┗━┛┗━┛┗━┛┗━┛