レオン・ワルラス Leon Walras 『純粋経済学要論 』:メモ
http://nam-students.blogspot.jp/2015/11/leon-walras_3.html
NAMs出版プロジェクト: パレート最適:メモ
http://nam-students.blogspot.jp/2015/04/blog-post_82.html(本頁)
経済学提要パレートManuale d’economia politica (1906)Vilfredo-Pareto
https://nam-students.blogspot.com/2020/02/blog-post_11.html
ソシュール(Ferdinand de Saussure、1857 - 1913)
https://nam-students.blogspot.com/2019/03/ferdinand-de-saussure1857-1913.html
パレートからソシュールへ 村舘論考
https://dl.ndl.go.jp/view/download/digidepo_10487043_po_ART0010353408.pdf
参考:ゲーム理論で解明されたユダヤの知恵
http://nam-students.blogspot.jp/2012/11/blog-post_28.html
ナッシュ均衡
ゲーム理論入門/(7)映画「ビューティフル・マインド」について - himaginaryの日記
http://d.hatena.ne.jp/himaginary/20080826/game_7
ナッシュ均衡
NON-COOPERATIVE GAMES
John Nash 1951
ピケティがパレート(の法則)を批判していたがそれは正しいと思う。どんな法則でもその法則に合うように恣意的にデータを選ぶことができる。
http://oshiete.goo.ne.jp/qa/1490263.html
厚生経済学の第一基本定理:
競争的均衡(ワルラス均衡)は存在するならば、それはパレート最適である。
厚生経済学の第二基本定理:
凸環境のもとで、各々の主体がすべての財の量を正の値で所有するような任意の配分は、所得を適切に再配分することによって、競争均衡として実現可能である。
第一定理は、全ての競争均衡は、ある人の効用を他者に害を与える事なしに大きくすることが出来ない点(パレート最適な点)として存在していることを示していますが、各人の平等性その他については全く言及していません。
それに対して第二定理は、望ましいパレート最適な点は適当な再配分を行えば競争均衡として実現できるということを示しています。
http://mikumaku.com/01/micro04.htm
(1)パレート効率性
資源配分において、他の人の効用を減少させないことには、ある人の効用を増加させることができない状態のことを(パレート効率的)であるという。他の人の効用を減少させずに、ある人の効用を増加させることができるような変化のことを(パレート改善)という。エッジワースのボックス・ダイアグラムにおいて、2人の個人の無差別曲線の(接点)ではパレート効率的な資源配分が達成されている。ここから、パレート効率性の条件として、(ある個人の限界代替率=他の個人の限界代替率)があげられる。これらを結んだ曲線を(契約曲線)という。
(2)厚生経済学の基本定理
交換が直接おこなわれなくても、価格調整でパレート効率的な資源配分が達成される。このような均衡を(競争均衡〔ワルラス均衡〕)という。競争均衡の条件は(ある個人の限界代替率=別の個人の限界代替率=価格比)である。厚生経済学の第1定理。(完全競争市場)ではパレート効率的な資源配分が達成される。厚生経済学の第2定理。最初に政府が適切な(所得分配)をおこなえば、任意のパレート効率的な資源配分を達成させることができる。
エッジワースのボックス
Aさんのキノコ
B_|_________0 Bさん
さ |\ o |
ん | \ |
の | \ o |
魚 |o \ |
| oXo |
| o\o |
| o\ o|
| o\ |
0|______o_\|_Aさんの魚
Aさん |
Bさんの
きのこ
AとBとの間に利益の一致点がある。
Aさんのキノコ
B_|_________0 Bさん
さ | o |
ん | |
の | o |
魚 |o |
| oXo |
| o o |
| o o|
| o |
0|______o__|_Aさんの魚
Aさん |
Bさんの
きのこ
Aさんのキノコ
B_|_________0 Bさん
さ |\ o |
ん | \ |
の | \ o |
魚 |o \ |
| oXo |
| o\o |
| o\ o|
| o\ |
0|______o_\|_Aさんの魚
Aさん |
Bさんの
きのこ
AとBとの間に利益の一致点がある。
Aさんのキノコ
B_|_________0 Bさん
さ | o |
ん | |
の | o |
魚 |o |
| oXo |
| o o |
| o o|
| o |
0|______o__|_Aさんの魚
Aさん |
Bさんの
きのこ
AとBとの間に利益の一致点Xがある。
多目的最適化手法の適用効果:川重テクノロジーWebマガジン[Techno Now]
http://www.kawaju.co.jp/techno-wm/showroom/32-1.html
3)パレート最適解
お互いに競合する複数の目的関数のもとで最適化を行うと普通はパレート最適解となります。パレート最適解とは「優劣がつけられない解」の集合のことで、「目的関数値のいずれかを改善しようとした場合、他の目的関数値が改悪されてしまうような状態」ともいえます。
ここでパレート解集合が形成する面のことをパレート解析フロントと呼び、図に示すように一般にパレート最適解は複数存在し、どの解を選択するかを判断することになります
ここでパレート解集合が形成する面のことをパレート解析フロントと呼び、図に示すように一般にパレート最適解は複数存在し、どの解を選択するかを判断することになります
的|
関| o @
数| o
2| ↙︎ o o パレート最適解フロント
| 最適化の方向
|______________
目的関数1
関| o @
数| o
2| ↙︎ o o パレート最適解フロント
| 最適化の方向
|______________
目的関数1
今回は「エッジワースの箱の中のパレート最適点」を見ていきます♪^ー^
その前にちょっとだけ復習を!
パレート最適というのは
相手の状態を悪くしないことには、もはや自分の状態を良くすることが出来ない
という状態のことです。これをよく覚えておいてくださいな。^○^
さて、ではちょっとエッジワースの箱を一つ描いてみましょうか♪
図23-1
↑はい、今回はこの図を使って説明します♪^ー^
結構複雑な図ですが、とりあえず
青い線(A1、A2、A3)はAさんの無差別曲線、
緑の線(B1、B2、B3)はBさんの無差別曲線、
赤い点は2人の初期保有量、
それ以外に紫の点(Ⅰ、Ⅱ)があることを確認してくださいな。^○^
で、とりあえず今の2人の効用水準は
Aさんの効用水準・・・A1
Bさんの効用水準・・・B1
ということが図から読み取れますね♪^ー^ (初期保有量を通る無差別曲線)
で、ここで例えば紫の点Ⅰの状態になるように、
2人の間で交換がなされたとすると、効用水準が
Aさんの効用水準・・・A2
Bさんの効用水準・・・B1
というように、
Bさんの効用を下げることなくAさんの効用が上がりました!!!
(無差別曲線は、自分の原点側から見て右上にあるほど効用水準が高い)
なので、この交換によって
パレート改善できた、といえますね♪^ー^
あっと、パレート改善というのは覚えていますでしょうか???´_`
パレート改善とは
他の誰の状態も悪くすることなく、誰か(もしくはみんな)の状態が良くなる
ということですよ~♪(復習)
で、さらにこのⅠ点からⅡ点の状態になるように交換したらどうなるでしょう?
今度は効用水準が
Aさんの効用水準・・・A2
Bさんの効用水準・・・B2
というように、
Aさんの効用を下げることなくBさんの効用が上がりました!!!
よって、この交換でもパレート改善できたということになりますね♪^○^
ここからがポイント!!!
ではこのⅡ点から他の状態に移るような交換をすると、
2人の効用水準はどうなるでしょう??? ̄~ ̄
例えば、ここより右上の点に行くと、Aさんの効用は上がってもBさんの効用は下がる
というのがわかります。T_T
同じように
ここより左下の点・・・Bさんの効用上がる、Aさんの効用下がる
ここより右下や左上・・・どちらの効用も下がる
↑つまり、Ⅱ点からだと右上・左下・左上・右下のどの点に変化しても
少なくとも一方の効用は下がってしまう、ということですね。。。T_T
ということは、
Ⅱ点はパレート最適な状態だといえますね♪^▽^
(どちらかの効用を上げようとすると、どちらかの効用が下がる)
で、結論から先に言ってしまうと、
パレート最適な点では、2人の無差別曲線が必ず接しています。
(「交わる」ではなく『接する』というのがポイントです!)
今回の図でも、Ⅱ点では確かに
Aさんの無差別曲線(A2)とBさんの無差別曲線(B2)が接していますね♪^○^
(交わらずくっついているでしょ?)
寒さ厳しい2月も終わりようやく春めいた気候になってきました。
このまま春の陽気が、続くと良いですね。3月に入り、年度末を迎えられる会社も多いと思います。
今回は「より良いビジネスライフのために」をテーマにお話ししたいと思います。
皆様は「パレートの法則」についてご存じでしょうか?
パレートの法則は、別名2:8の法則とも言われています。
例えば、
・売上の8割は全顧客の2割が生み出している。よって売上を伸ばすには
顧客全てを対象としたサービスを行うよりも、2割の顧客に的を絞ったサービスを行う方が効率的である。
・商品の売上の8割は、全商品銘柄のうちの2割で生み出している。
・売上の8割は、全従業員のうちの2割で生み出している。
・仕事の成果の8割は、費やした時間全体のうちの2割の時間で生み出している。
・全体の20%が優れた設計ならば実用上80%の状況で優れた能力を発揮する。
(1) 他の事情が不変ならば,国民分配分の増大は経済的厚生を増大する傾向がある(成長), (2)… 略…(平等), (3) 国民分配分の変動が少くなるほど経済的厚生が増大する傾向がある(安定),
将来消費C2
|
|
|o
| o
| o
| ↗︎ o
| ↗︎
| o
|_______o____現在消費C1
C1とC2とで異なる世代の消費。↗︎は成長。
http://www.apu.ac.jp/~wave/game/index.html
A Collective Action Problem (囚人のジレンマ)
参考文献
岡田章『ゲーム理論』有斐閣、1996年、pp406.
A Collective Action Problem (囚人のジレンマ)
____________________
| |____イケメン弟____|
|______|__うそ__|__正直__|
| |うそ|パレート最適| A1,B2|
|イケ |__|______|______|
|メン兄|正直| A2,B1|ナッシュ均衡|
|___|__|______|______|
参考文献
岡田章『ゲーム理論』有斐閣、1996年、pp406.
なお、市場主義はナッシュ均衡点がパレート効率的であるようにする試みの一つである。
_________
http://crossacross.org/ky/?Poilitics+Pareto+optimality+Nash+equilibrium
世の中は、個人の利益と社会全体の福利厚生がある。各々が個人の利益を追求した場合の結末をナッシュ均衡(点)と呼び、社会システム全体の福利厚生が最大限まで達成されている「最大多数の最大幸福」の状態をパレート効率的であると言う。
この両者が一致していれば放っておいても皆幸せになるが、必ずしも一致するわけではない*1。「誰か1人が犠牲になれば他全員が助かる」「何もしなければ50%の確率で全滅する」という選択があれば、みんな自分がかわいいので自分の被害を最小化する選択をとり、後者の選択をとる(ナッシュ均衡)。しかし、全体としてみれば、利益の期待値は前者の選択のほうが明らかに大きい(パレート最適)。
ナッシュ均衡は個々人の利益の追求の結果だが、それがみんなの幸せであるパレート最適と一致しているとは限らない。また、為政者はパレート効率性を追求しがちだが、そこには幸福の不公平性が常に見え隠れする。
*1 なお、市場主義はナッシュ均衡点がパレート効率的であるようにする試みの一つである。
______
http://blog.livedoor.jp/yoshihisa_sr/archives/3275216.html
「ナッシュ均衡」について書こうと思いますが、数学的な要素がありますので「なに言っとるねん」とならないように(?)身近な例でわかりやすく(どうだか…?)しようと思います。
ナッシュ均衡とは数学者ジョン・フォーブス・ナッシュによって考えられたゲーム理論の非協力ゲームの答えの一つとされています。
例えば会議などでAさんBさんがC案にするかD案にするかと言った議論をします。お互い議論はしますがお互いに最適な案を選択をして、「Aさん(またはBさん)の主張するC案(またはD案)が決まれば、その案を成功させるためにじゃあお互い協力しよう」とお互い変更する動機がなくなり安定した状態になる事です。「落としどころ」という言葉がありますが、よく似ています。
こちらのブログにある「囚人のジレンマ」では、「お互い自白すること」が自身にとっては釈放されると言う最適な選択になるため「ナッシュ均衡」と言われているものです。
また「男女の争い」というものがあります。上記のAさんBさんともに押し通すと、お互い良い結果は生まれませんよね。「男女の争い」は最後には協調して一致する行動をとることにはお互い同意していますが、協調の方法については異なる選択を主張する意味合いがあります。
よくある身近な例ですが、なかなか会えない恋人たちが日曜日にやっと会うことが出来ました。男性は「外でデート」、女性は「家でまったりしたい」と主張します。このカップル、女性の方が強いらしく、意見は女性の主張が通り「家でまったり」することになりました。男性は少し不満がありましたが、「彼女と久しぶりにあえたんだから、少し不満でもまぁいっか」となりました。
ナッシュ均衡に落ち着くと、それが納得できなくても選択を変更する動機が働かないことが特徴とされています。(もし男性が「外でデートする」と主張を押し通せば、双方納得できずにお互いバラバラになり喧嘩になりますよね。最悪は「バイバイ~」となりかねません)
上記のAさんとBさんも「男女の争い」とも言えます。ナッシュ均衡は複数のあるのが普通なので、ビジネス上では一方が低レベルに落ち着けば、均衡点のレベルがスパイラル的に落ちてしまう事があるので気を付けたいものです。
このまま春の陽気が、続くと良いですね。3月に入り、年度末を迎えられる会社も多いと思います。
今回は「より良いビジネスライフのために」をテーマにお話ししたいと思います。
皆様は「パレートの法則」についてご存じでしょうか?
パレートの法則は、別名2:8の法則とも言われています。
例えば、
・売上の8割は全顧客の2割が生み出している。よって売上を伸ばすには
顧客全てを対象としたサービスを行うよりも、2割の顧客に的を絞ったサービスを行う方が効率的である。
・商品の売上の8割は、全商品銘柄のうちの2割で生み出している。
・売上の8割は、全従業員のうちの2割で生み出している。
・仕事の成果の8割は、費やした時間全体のうちの2割の時間で生み出している。
・全体の20%が優れた設計ならば実用上80%の状況で優れた能力を発揮する。
///////////
参考:
NAMs出版プロジェクト: ピグーの不遇:メモ
http://nam-students.blogspot.jp/2015/04/blog-post_78.html
厚生経済学の第二基本定理
厚生経済学の第2定理・・・財の総量を一定としたときの任意のパレート最適な配分は、適当な初期保有量の再分配から出発する市場均衡として達成される。
(上記定義は、ドーフマン、サミュエルソン、ソロー『線型計画と経済分析』1958年より)
|\ o
| \
x2| \ o X
|o \
| o\o
| o\o
| Y o\ o o
| o\
|______o_\____
x1
X消費、Y生産。一致点がある。
厚生経済学の第2定理・・・財の総量を一定としたときの任意のパレート最適な配分は、適当な初期保有量の再分配から出発する市場均衡として達成される。
(上記定義は、ドーフマン、サミュエルソン、ソロー『線型計画と経済分析』1958年より)
|\ o
| \
x2| \ o X
|o \
| o\o
| o\o
| Y o\ o o
| o\
|______o_\____
x1
X消費、Y生産。一致点がある。
上記図は、神取道宏『ミクロ経済学の力』(502頁~)より
☆
厚生経済学の第一、第三命題
厚生経済学の第一、第三命題
将来消費C2
|
|
|o
| o
| o
| ↗︎ o
| ↗︎
| o
|_______o____現在消費C1
C1とC2とで異なる世代の消費。↗︎は成長。
(本郷図解名古屋大学出版2007年,129頁)
パレートの法則
________________
/\ ̄ ̄ ̄ ̄ ̄ ̄ ̄\ /
/__\ 2:8 \ /
/ \ ̄-_ \ /
/ \  ̄-_ \ /
/ \  ̄-_\ /
/ \  ̄\____/
/ \ \ /
/______________\ \/
行動時間 成果
顧客数 etc. 売上 etc.
________________
/\ ̄ ̄ ̄ ̄ ̄ ̄ ̄\ /
/__\ 2:8 \ /
/ \ ̄-_ \ /
/ \  ̄-_ \ /
/ \  ̄-_\ /
/ \  ̄\____/
/ \ \ /
/______________\ \/
行動時間 成果
顧客数 etc. 売上 etc.
参考:
NAMs出版プロジェクト: ピグーの不遇:メモ
NAMs出版プロジェクト: ピケティ関連:メモ
http://nam-students.blogspot.jp/2015/01/blog-post_30.html
http://nam-students.blogspot.jp/2015/01/blog-post_30.html
ゲーム理論で解明されたユダヤの知恵
http://nam-students.blogspot.jp/2012/11/blog-post_28.html
http://nam-students.blogspot.jp/2012/11/blog-post_28.html
神取道宏『ミクロ経済学の力』(2014年、日本評論社):書評&目次
http://nam-students.blogspot.jp/2015/02/blog-post_82.html
(f) 交換経済の分析:エッジュワースの箱 219
二人の消費者による二つの財の資源配分を大きな箱の中の無差別曲線で表す。これを考案した経済学者F.Y.エッジュワースの名前をとってエッジュワースの箱という。
図3.38 エッジュワースの箱
_______⬅︎Bが消費する第1財_0B
| ____ |
⬆︎ | Aの無差別 ___ \ |B
A | | 曲線 _ \ ↙︎ |が
が | | | | \ ↙︎ \ |消第
消第| \ \ ↗︎ ↙︎ \ \|費2
費2| \ ↗︎ \_ | | ||す財
す財| ↗︎ \___ Bの無差別 |る
る | \____ 曲線 | ⬇︎
|__________________|
0A Aが消費する第1財➡︎
(↗︎↙︎効用の上がる方向)神取220頁
||
\/
図3.38 エッジュワースの箱(パレート最適を加筆)
________⬅︎Bが消費する第1財__0B
| |
⬆︎ |Bの無差別 | |B
A |曲線 ____ | |が
が | \\ |消第
消第| [] Aの無差別|費2
費2| \\____ 曲線|す財
す財| | |る
る | ︎ | | ⬇︎
|____________________|
0A Aが消費する第1財➡︎
(↗︎↙︎効用の上がる方向、[]パレート効率的な配分=パレート最適=ゲーム理論で言うコア、核)
以下は、「資源配分の効率性とは何か」という条件を高度に一般的かつコンパクトにまとめたもの。
X2
| | これだけあれば、全員
| | X の効用を現状の水準以
|________ | 上にできる
| \\
| []総消費点
| Y \\________
| これだけ作れる |
| ︎ |
|____________________x1
図D.6 パレート効率性は、改善集合Xと生産可能性Y
が接していることを意味する(513頁)
http://www.apu.ac.jp/~wave/game/index.html
A Collective Action Problem (囚人のジレンマ)
| イケメン兄 |  | 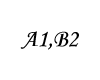 | |
 |  | ||
参考文献
岡田章『ゲーム理論』有斐閣、1996年、pp406.
A Collective Action Problem (囚人のジレンマ)
____________________
| |____イケメン弟____|
|______|__うそ__|__正直__|
| |うそ|パレート最適| A1,B2|
|イケ |__|______|______|
|メン兄|正直| A2,B1|ナッシュ均衡|
|___|__|______|______|
参考文献
岡田章『ゲーム理論』有斐閣、1996年、pp406.
なお、市場主義はナッシュ均衡点がパレート効率的であるようにする試みの一つである。
http://crossacross.org/ky/?Poilitics+Pareto+optimality+Nash+equilibrium
世の中は、個人の利益と社会全体の福利厚生がある。各々が個人の利益を追求した場合の結末をナッシュ均衡(点)と呼び、社会システム全体の福利厚生が最大限まで達成されている「最大多数の最大幸福」の状態をパレート効率的であると言う。
この両者が一致していれば放っておいても皆幸せになるが、必ずしも一致するわけではない*1。「誰か1人が犠牲になれば他全員が助かる」「何もしなければ50%の確率で全滅する」という選択があれば、みんな自分がかわいいので自分の被害を最小化する選択をとり、後者の選択をとる(ナッシュ均衡)。しかし、全体としてみれば、利益の期待値は前者の選択のほうが明らかに大きい(パレート最適)。
ナッシュ均衡は個々人の利益の追求の結果だが、それがみんなの幸せであるパレート最適と一致しているとは限らない。また、為政者はパレート効率性を追求しがちだが、そこには幸福の不公平性が常に見え隠れする。
*1 なお、市場主義はナッシュ均衡点がパレート効率的であるようにする試みの一つである。
______
http://blog.livedoor.jp/yoshihisa_sr/archives/3275216.html
「ナッシュ均衡」について書こうと思いますが、数学的な要素がありますので「なに言っとるねん」とならないように(?)身近な例でわかりやすく(どうだか…?)しようと思います。
ナッシュ均衡とは数学者ジョン・フォーブス・ナッシュによって考えられたゲーム理論の非協力ゲームの答えの一つとされています。
例えば会議などでAさんBさんがC案にするかD案にするかと言った議論をします。お互い議論はしますがお互いに最適な案を選択をして、「Aさん(またはBさん)の主張するC案(またはD案)が決まれば、その案を成功させるためにじゃあお互い協力しよう」とお互い変更する動機がなくなり安定した状態になる事です。「落としどころ」という言葉がありますが、よく似ています。
こちらのブログにある「囚人のジレンマ」では、「お互い自白すること」が自身にとっては釈放されると言う最適な選択になるため「ナッシュ均衡」と言われているものです。
また「男女の争い」というものがあります。上記のAさんBさんともに押し通すと、お互い良い結果は生まれませんよね。「男女の争い」は最後には協調して一致する行動をとることにはお互い同意していますが、協調の方法については異なる選択を主張する意味合いがあります。
よくある身近な例ですが、なかなか会えない恋人たちが日曜日にやっと会うことが出来ました。男性は「外でデート」、女性は「家でまったりしたい」と主張します。このカップル、女性の方が強いらしく、意見は女性の主張が通り「家でまったり」することになりました。男性は少し不満がありましたが、「彼女と久しぶりにあえたんだから、少し不満でもまぁいっか」となりました。
ナッシュ均衡に落ち着くと、それが納得できなくても選択を変更する動機が働かないことが特徴とされています。(もし男性が「外でデートする」と主張を押し通せば、双方納得できずにお互いバラバラになり喧嘩になりますよね。最悪は「バイバイ~」となりかねません)
上記のAさんとBさんも「男女の争い」とも言えます。ナッシュ均衡は複数のあるのが普通なので、ビジネス上では一方が低レベルに落ち着けば、均衡点のレベルがスパイラル的に落ちてしまう事があるので気を付けたいものです。








22 Comments:
ヴィルフレド・パレート
ローザンヌ学派
ヴィルフレド・パレート
生誕 1848年7月15日
フランス共和国 パリ
死没 1923年8月19日(75歳)
スイス セリニー
国籍 イタリア
研究分野 厚生経済学
ミクロ経済学
社会経済学
影響を
受けた人物 レオン・ワルラス
影響を
与えた人物 タルコット・パーソンズ
ルイジ・アンローゾ
Alain de Benoist
実績 パレート・インデックス
パレート図
パレートの法則
パレート効率性(パレート最適)
パレート分布
パレート原理
テンプレートを表示
ヴィルフレド・パレート(Vilfredo Frederico Damaso Pareto、1848年7月15日 - 1923年8月19日)はイタリアの技師、経済学者、社会学者、哲学者。
目次
生涯
経済学上の功績
社会学上の功績
主な著作
参考文献
脚注
関連項目
生涯編集
パレートは、1848年にパリで生まれた。パレートがイタリア国外で生まれた理由は、彼の父が、自由主義革命家マッツィーニの指導する青年イタリア党の革命運動に参加して官憲の追及を受けたため、パリに亡命して、その地でフランス人女性と結婚したためである。
パレートは当初、理数系の道を進み、トリノ工科大学で数学、物理学、建築学を修めた。卒業後は鉄道会社に技師として就職するが、父親の影響からか政治の世界への関心を強め、自由主義の立場から政府批判を展開し、積極的な政治活動を行った。その結果、社会的地位が脅かされるようになり、会社を退職して一時的にスイスで隠遁生活を送るようになる。
その後、ある自由主義経済学者の紹介によって純粋経済学の大家レオン・ワルラスと知り合い、ワルラスの影響から経済学の研究に分け入っていくことになった。やがて、その研究実績が認められ、1893年にワルラスの後任としてローザンヌ大学で経済学講座の教授に任命された。彼はそこで、経済学における一般均衡理論(ローザンヌ学派)の発展に貢献し、さらに厚生経済学という新たな経済学の分野を開拓した。
20世紀に至って、パレートの学問的な関心は経済学から社会学へと移って行き、それと同時に自由主義的・民主主義的な思想・運動への批判を強めていった。これは、彼の政治活動の失敗や自由主義・民主主義への幻滅によるものだとも考えられる。
第一次世界大戦後には、ジョルジュ・ソレルに招かれたこともある。ソレルの信奉者だったパレートはベニート・ムッソリーニを評価したため、彼の社会学理論はファシスト体制御用達の反動理論との批判を受けるようになった。フィリッポ・トゥラーティの主宰する雑誌に寄稿する[1]など社会主義者とも交流しており、ムッソリーニは社会主義者時代にパレートの講義を聴講したことがあった。
晩年において、病に冒されながらも精力的に社会学の体系化を試みるが、その途上、1923年に75歳でその生涯を閉じた。
経済学上の功績編集
パレートは、ワルラスの均衡理論を発展させ、「パレート効率性(パレート最適)」という資源の生産および消費における最適かつ極限の状態を概念として提起したことで知られている。これは、一定量の資源を複数の人間が利用する場合において、個人の効用(満足度)が他者の効用を損なうことなく、極限まで高められた状態(配分について交渉を行う余地の無い状態)のことを意味している。つまり、「パレート効率性」とは、資源の有効活用の原理ということができる。
さらに彼は、数理経済学の実証的な手法(統計分析)を用いて、経済社会における富の偏在(所得分布の不均衡)を明らかにした。これはパレートの法則とよばれている。この法則は、2割の高額所得者のもとに社会全体の8割の富が集中し、残りの2割の富が8割の低所得者に配分されるというものである。
パレートは、このような概念によって、社会全体の福利の適正配分と効用の最大化を目指す経済政策を理論的に基礎づけ、厚生経済学におけるパイオニア的存在となった。
社会学上の功績編集
パレートは、それまでの経済学における研究業績を応用し、実証主義的方法論に基づいて社会の分析を行っていった。もともと自然科学を出発点として経済学・社会学の分野へと進んだパレートは、実験と観察によって全体社会のしくみ、および変化の法則を解明しようとした。
特に、経済学における一般均衡の概念を社会学に応用し、全体社会は性質の異なるエリート集団が交互に支配者として入れ替わる循環構造を持っているとする「エリートの周流」という概念を提起したことで知られている。そしてパレートは、2種類のエリートが統治者・支配者として交代し続けるという循環史観(歴史は同じような事象を繰り返すという考え方)に基づいて、19世紀から20世紀初頭のヨーロッパで影響力を持っていた社会進化論やマルクス主義の史的唯物論(唯物史観)を批判した。
さらに、人間の行為を論理的行為(理性的行為)と非論理的行為(非理性的行為)に分類し、経済学における分析対象を人間の論理的行為に置いたのに対し、社会学の主要な分析対象は非論理的行為にあると考えた。つまり現実の人間は、感情・欲求などの心理的誘因にしたがって行動する非論理的傾向が強く、しかも人間の非論理性が社会の構造を規定しているとみなしたのである。このような行為論は、その後アメリカの社会学者タルコット・パーソンズの社会システム論に影響を与えることになった。
パレートは、初期の総合社会学にはない新しい視点に立ち、独自の社会学理論を構築したところから、マックス・ヴェーバーやエミール・デュルケームと並ぶ重要な社会学者の1人として位置づけられている。
主な著作編集
経済学講義(Cour d'Economie Politique, Laussanne. 1896)
一般社会学大綱(Trattato di sociologia generale. 1917-19)
参考文献編集
ヴィルフレド・パレート(北川隆吉、板倉達文、広田明訳)『社会学大綱』(現代社会学体系・青木書店)ISBN-10:4250870448
作田啓一、井上俊編『命題コレクション 社会学』(筑摩書房)ISBN-10:4480852921
田原音和・田野崎昭夫・阿閉吉男他著(新明正道監修)『現代社会学のエッセンス 社会学理論の歴史と展開(改訂版)』(ぺりかんエッセンスシリーズ・ぺりかん社)ISBN-10: 4831507210
脚注編集
^ 佐藤茂行『パレート社会主義論の形成』經濟學研究、1991年
関連項目編集
パレート図
パレート効率性(パレート最適)
パレートの法則
パレート分布
パレート分析
パレート改善
別の言語で閲覧
パレートの法則 ̄
________________
/\ \ /
/__\ \ /
/ \ 2:8 \ /
/ \ \ /
/ \ \ /
/ \ \____/
/ \ \ /
/______________\ \/
行動時間 成果
顧客数 etc. 売上 etc.
パレートの法則
________________
/\ ̄ ̄ ̄ ̄ ̄ ̄ ̄\ /
/__\ \ /
/ \ ̄-_2:8 \ /
/ \  ̄-_ \ /
/ \  ̄-_\ /
/ \  ̄\____/
/ \ \ /
/______________\ \/
行動時間 成果
顧客数 etc. 売上 etc.
エッジワースのボックス
Aさんのキノコ
B_|_________Bさん
さ |\ o |
ん | \ |
のB| \ o |
魚 |o \ |
| o\o |
| o\o |
| o\ o|
| o\ |
|______o_\|_Aさんの魚
Aさん |
Bさんの
きのこ
AとBとの間に利益の一致点がある。
Aさんのキノコ
B_|_________Bさん
さ | o |
ん | |
のB| o |
魚 |o |
| oxo |
| o o |
| o o|
| o |
|______o__|_Aさんの魚
Aさん |
Bさんの
きのこ
AとBとの間に利益の一致点xがある。
(f) 交換経済の分析:エッジュワースの箱 219
エッジワースのボックス
Aさんのキノコ
B_|_________0 Bさん
さ |\ o |
ん | \ |
の | \ o |
魚 |o \ |
| oXo |
| o\o |
| o\ o|
| o\ |
0|______o_\|_Aさんの魚
Aさん |
Bさんの
きのこ
AとBとの間に利益の一致点がある。
図3.38 エッジュワースの箱
___________________0B
| ____ |
| Aの無差別 ___ \ |
| | 曲線 _ \ ↙︎ |
| | | | \ ↙︎ \ |
| \ \ ↗︎ ↙︎ \ \ |
| \ ↗︎ \_ | | | |
| ↗︎ \___ Bの無差別 |
| \____ 曲線 |
|___________________|
0A (↗︎↙︎効用の上がる方向)神取220頁
図3.38 エッジュワースの箱
(↗︎↙︎効用の上がる方向)
___________________0B
| ____ |
| ___ \ |
| | _ \ ↙︎ |
| | | | \ ↙︎ \ |
| \ \ ↗︎ ↙︎ \ \ |
| \ ↗︎ \_ | | | |
| ↗︎ \___ Bの無差別曲線|
| \____Aの無差別曲線 |
|___________________|
0A
図3.38 エッジュワースの箱
(↗︎↙︎効用の上がる方向)
____________________0B
| ____ |
| ___ \ |
| | _ \ ↙︎ |
| | | | \ ↙︎ \ |
| \ \ ↗︎ ↙︎ \ \ |
| \ ↗︎ \_ | | | |
| ↗︎ \___ Bの無差別曲線|
| \____Aの無差別曲線 |
|____________________|
0A
図3.38 エッジュワースの箱
(↗︎↙︎効用の上がる方向)
____________________0B
| ____ |
| ___ \ |
| | _ \ ↙︎ |
| | | | \ ↙︎ \ |
| \ \ ↗︎ ↙︎ \ \ |
| \ ↗︎ \_ | | | |
| ↗︎ \___ | |
| \____ |
|____________________|
0A
図3.38 エッジュワースの箱
(↗︎↙︎効用の上がる方向)
____________________0B
|↗︎↙︎効用の上がる方向____ |
| ___ \ |
| | _ \ ↙︎ |
| | | | \ ↙︎ \ |
| \ \ ↗︎ ↙︎ \ \ |
| \ ↗︎ \_ | | | |
| ↗︎ \___ | |
| \____ |
|____________________|
0A
図3.38 エッジュワースの箱
図3.38 エッジュワースの箱
___________________0B
| ____ |
| Aの無差別 ___ \ |
| | 曲線 _ \ ↙︎ |
| | | | \ ↙︎ \ |
| \ \ ↗︎ ↙︎ \ \ |
| \ ↗︎ \_ | | | |
| ↗︎ \___ Bの無差別 |
| \____ 曲線 |
|___________________|
0A (↗︎↙︎効用の上がる方向)神取220頁
図3.38 エッジュワースの箱
___________________0B
| ____ |
| Aの無差別 ___ \ |
| | 曲線 _ \ ↙︎ |
| | | | \ ↙︎ \ |
| \ \ ↗︎ ↙︎ \ \ |
| \ ↗︎ \_ | | | |
| ↗︎ \___ Bの無差別 |
| \____ 曲線 |
|___________________|
0A (↗︎↙︎効用の上がる方向)神取220頁
図3.38 エッジュワースの箱
___________________0B
| ____ |
| Aの無差別 ___ \ |
| | 曲線 _ \ ↙︎ |
| | | | \ ↙︎ \ |
| \ \ ↗︎ ↙︎ \ \ |
| \ ↗︎ \_ | | | |
| ↗︎ \___ Bの無差別 |
| \____ 曲線 |
|___________________|
0A (↗︎↙︎効用の上がる方向)神取220頁
図3.38 エッジュワースの箱
___________________0B
| ____ |
| Aの無差別 ___ \ |
| | 曲線 _ \ ↙︎ |
| | | | \ ↙︎ \ |
| \ \ ↗︎ ↙︎ \ \ |
| \ ↗︎ \_ | | | |
| ↗︎ \___ Bの無差別 |
| \____ 曲線 |
|___________________|
0A (↗︎↙︎効用の上がる方向)神取220頁
http://gametheory.jp/page.php?id=47
合理的は望ましい??パレート最適とナッシュ均衡3
このように、囚人のジレンマの状況では「お互いが合理的に動いた」結果、「2人にとって悪い結果」になってしまった。
では、2人とも自白しようとしている状態から、2人とも黙秘するという、お互いにとって良い結果があるとわかったのだから、パレート最適である状態であるその状態に移ることはできないのだろうか?そうすれば2人にとって望ましいではないか…
しかしこれはできないのだ。
今はお互い連絡を取ることはできない。とすると、「2人とも自白」から「2人とも黙秘」という結果に移動するには、下の斜めの矢印のような1歩の移動ではなく、2つの矢印が合わさった2歩の移動しかできないのだ。
(上へはルパンが自白から黙秘に行動を変えることで、左へは次元が自白から黙秘に行動を変えることで、それぞれ移動できる。)
ルパンも次元も「2人とも自白」という状態から「自分だけが行動を変える」と損をしてしまうので、相手の出方がわからない中では、合理的に判断した場合に、自白に変えることはできず、こうして2人とも自白という状態から、このままでは抜け出すことができないのだ。
このような「みんながみんな、自分だけが行動を変えても、得をしない状態」のことをナッシュ均衡という。ナッシュ均衡はゲーム理論で考えたときに起こる結果(ゲームの解)だ。つまりナッシュ均衡がわかれば、そのゲームで起こる結果が予想できる。そして、今回のように、お互いが支配戦略をとった結果は、必ずナッシュ均衡になる。
ここまで見て分かるとおり、2人にとって望ましいとされるパレート最適な状態と、2人が合理的に動いた結果のナッシュ均衡は、一致するとは限らない。そして、一度ナッシュ均衡に陥ってしまうと、均衡という言葉の通り、2人にとってより良い結果がたとえあったとしても、残念ながら、このままでは脱出不可能なのだ。
前のページへ 次のページへ
ナッシュ均衡 - Q-BPM
ja.q-bpm.org/mediawiki/index.php/ナッシュ均衡
ナッシュ均衡 (Nash equilibrium) とは、主体が他者との協力なしに自らの利益を最大 化しようと行動した時の状態で、実際には自らも他者も利益を最大化していない状態に なることもある。 目次. 1 概要; 2 ナッシュ均衡と最適状態. 2.1 囚人のジレンマ; 2.2 男女 ...
ジョン・ナッシュの業績 - 一橋大学経済学研究科 (Adobe PDF) -htmlで見る
www.econ.hit-u.ac.jp/~aokada/essay_pdf/John_final.pdf
の他にナッシュ均衡という概念を学ばれることと思います。 ナッシュ均衡は、数学者で ゲーム理論家であり、今年度のアカデミー賞最優秀作品賞を. 受賞した映画「 ビューティフルマインド」のモデルとなったジョン・ナッシュ(John F. Nash. Jr.) が定式化 したゲームや ...
2×2双行列ゲームのナッシュ均衡 混合戦略のナッシュ均衡 (Adobe PDF) -htmlで見る
www2.rku.ac.jp/mnakayama/pdf/nashequilibria.pdf
2015年4月20日 ... 2015/4/20. 2. • 2×2双行列ゲームにおいて. –. 純粋戦略ナッシュ均衡が存在しない. –. どのプレイヤーも支配される戦略をもたない. ならば,2個の純粋戦略は均衡で正の 確率で用い. られる. ゆえに,2個の純粋戦略の期待利得は等しい. 注意.
ナッシュ均衡とは | ビジネススクールならグロービス・マネジメント・スクール
gms.globis.co.jp>...>MBA用語集>交渉術・ゲーム理論
ナッシュ均衡についての意味や説明。MBA用語集。 短期間で実践的ビジネススキルが 身につく、社会人のためのビジネススクール。グロービス・マネジメント・スクール。 東京・ 大阪・名古屋で幅広いカリキュラムを1科目から受講可能。
2ページ目
ナッシュ均衡で知られる数学者ジョン・ナッシュが死去:享年86歳 ...
societas.blog.jp/1028522665
15時間前 ... 1928年生まれのジョン・ナッシュはプリンストン大学教授。ゲーム理論における非協力 ゲームの解の一種である「ナッシュ均衡」などの業績で知られ、1994年にはノーベル 経済学賞を受賞している。後半生は統合失調症に罹患し、長い闘病生活 ...
ナッシュ均衡とバブルファクターによる理論的格ゲー攻略法 : チゲ速
chigesoku3.doorblog.jp/archives/43175712.html
2015年2月2日 ... ナッシュ均衡やバブルファクターといった理論で格闘ゲームを攻略してみようという動画 がニコニコで公開されています。ポーカーをプレイする方は聞いた事のある言葉だと思い ますが、それを格ゲーに応用する事で誰でもウル4でPP3000以上に ...
囚人のジレンマとナッシュ均衡による理論的格闘ゲーム攻略法 : チゲ速
chigesoku3.doorblog.jp/archives/43272957.html
2015年2月9日 ... 以前、ナッシュ均衡とバブルファクターという考え方を格ゲーに応用する攻略法について の動画を紹介しましたが、その続編が公開されています。 part2となる今回のキーワード は『囚人のジレンマ』と『ナッシュの広げ方、狭め方』というもの。
ナッシュ均衡とは - 外国為替用語 Weblio辞書
www.weblio.jp>Weblio 辞書>同じ種類の言葉>言葉>状態>均衡
ナッシュ均衡とは?外国為替用語。 アメリカの数学者 J =ナッシュによるゲーム理論の 概念。すべてのプレーヤーが相手の戦略のもとで自分の利益を最大化するように行動し ているとき成立する均衡状態。 >>『三省堂 大辞林』の表記・記号について...
ナッシュ均衡の英語・英訳 - 英和辞典・和英辞典 Weblio辞書
ejje.weblio.jp>...>英和辞典・和英辞典>JMdict
ナッシュ均衡を英語に訳すと 読み方:ナッシュきんこう文法情報(名詞)対訳 Nash equilibrium - 約985万語ある英和辞典・和英辞典。発音・イディオムも分かる英語辞書 。
ナッシュ均衡解 (Adobe PDF) -htmlで見る
www.campus.ouj.ac.jp/~maps13/08_09/09Game2.pdf
ナッシュ均衡解. プレイヤーA. プレイヤーB. 戦略1. 戦略2. 戦略1 (40, 45) (30, 50). 戦略2 (50, 35) (20, 25). • 相手の戦略に対して自らの利得を最大にする戦略 …相手の 戦略に対する最適反応戦略. • 各プレイヤーのとる戦略が互いに相手の戦略に.
ゲーム理論のナッシュ均衡とは何だろう? - ナッシュ均衡入門 | ShareWis ...
press.share-wis.com/what-is-nash-equilibrium
ゲーム理論におけるナッシュ均衡とは、相手の戦略が分かっていて、相手が戦略を変え ないとして、自分だけが戦略変えると損をしてしまうような状況が全てのプレイヤーで 起こっている状況を指します。
ゲーム理論のナッシュ均衡とは何だろう? – ナッシュ均衡入門
2013年9月21日 · カテゴリー: ゲーム理論
ジョン・ナッシュがその理論を構築したナッシュ均衡。
ゲーム理論ではよく耳にする言葉ですが、このナッシュ均衡とは一体何なのでしょう?
ナッシュ均衡の定義
以下はWikipediaから引用したナッシュ均衡の定義です。
形式的な定義は次の通りである。標準型ゲーム G = (N, S, u) (N はプレーヤーの集合、 は戦略の組の集合、 は効用の組)において、戦略の組 がナッシュ均衡であるとは、全てのプレーヤー と、全ての に対して、
うーん…。
これって日本語?って言いたくなるくらい、よく分かりませんね。
簡単に言葉で説明すると、ナッシュ均衡とは相手の戦略が分かっていて、
相手が戦略を変えないとして、自分だけが戦略変えると損をしてしまうような状況が全てのプレイヤーで起こっている状況を指します。
自分だけ戦略を変えると損をするわけですから、自分は戦略を変えない方がいいという結論が導き出されます。
また、相手についても同じことが成り立っていると、相手も戦略を変えないほうがいい状態になります。
このような戦略の取り方をナッシュ均衡と言います。
ナッシュ均衡の例
恋人同士が待ち合わせをしているとします。
携帯など互いにコミュニケーションを取ることができない状況を考えます。
このとき、待合場所として改札前とコンビニ前があったとしたら、女性が改札前に行っていることがなんらかの形で知ることができたら、男性は改札前で待つ、という戦略を選ぶはずです。
もし、ここでコンビニ前を選んだなら彼女に会えないわけですから。
一方、彼女の方も同じような状況なので、彼が改札前で待っていることが分かったら、改札前で待つ、という戦略を選びます。
つまり、
男: 改札前
女: 改札前
というような状況はナッシュ均衡の状況といえます。
では、ナッシュ均衡はこの1種類だけでしょうか?
そんなことはありませんね。
男:コンビニ前
女:コンビニ前
もナッシュ均衡です。
このように、状況によって、ナッシュ均衡が複数ある状況や、あるいはナッシュ均衡が1つも存在しないような状況まであります。
ナッシュ均衡などゲーム理論について基本的な箇所を学習したい方は下記のコースがおすすめです!
無料学習iOSアプリShareWis
わたし達は「知識の地図」を使ったShareWiという学習アプリを運営しています。
スタッフ募集中!
関連する記事
「冒険」を軸に考える ”真の学習”
演繹法にも論理の飛躍はありますよという話
関連するみんなの記事
ナッシュ均衡とFPS
はじめてのゲーム理論 (ブルーバックス) [新書] 川越 敏司 (著)
ダブルコンティンジェンシーとは (double contingency) 用語解説 |
神取339頁
q2
|\
| \
| \
| \
|_ \
|  ̄-_ \
|  ̄-\
|  ̄-_
| \  ̄-_
| \  ̄-_
|__________\_____ ̄-_____
q1
クルーノー・ナッシュ均衡
クルーノー(数量競争、寡占時q1,q2)
神取339頁
q2
2|
|\
| \
| \
1|_ \
|  ̄-_\
|  ̄\E
|  ̄-_
| \  ̄-_
| \  ̄-_
|_________\_____ ̄-_____
1 2 q1
E=クルーノー・ナッシュ均衡
クルーノー(数量競争、寡占時q1,q2)
神取339頁
q2
2|
|\
| \
| \
1|_ \
o  ̄-_\
| o  ̄\E
|  ̄-_
| o \  ̄-_
| \  ̄-_
|________o\_____ ̄-_____
1 2 q1
E=クルーノー・ナッシュ均衡
クルーノー(数量競争、寡占時q1,q2)
o=最適生産量
神取339頁
q2
2|
|\
| \
| \
1|_ \
Q  ̄-_\
| o  ̄\E
|  ̄-_
| o \  ̄-_
| \  ̄-_
|________Q\_____ ̄-_____
1 2 q1
E=クルーノー・ナッシュ均衡
クルーノー(数量競争、寡占時q1,q2)
総生産量Q=q1+q2
独占企業の最適生産量
個々の企業にとって、
Q=最適生産量
国富論4:2に出てくる「見えざる手」はパレート最適を先取りしている。
《…かれはこのばあいに、他のおおくのばあいと同様に、みえない手にみちびかれて、かれの意図のどこにもなかったひとつの目的を、促進するようになるのである。』国富論4:2
見えざる手(みえざるて、英: an invisible hand)とは、アダム・スミスの『国富論』の第4 編第2章に現れる言葉である。 ... 最後の最終戦争には、信徒は神の見えざる手により 救済され、天国へ行くことができる」などの教えから来る物 ...
神の見えざる手(カミノミエザルテ)とは
kotobank.jp/word/神の見えざる手-466561 デジタル大辞泉 - 神の見えざる手の用語解説 - 市場において、各個人の利己的な行動 の集積が社会全体の利益をもたらすという調整機能。アダム=スミスが「国富論」で提唱 した。見えざる手。→市場原理[補説]神の見えざる手(invisible hand of God) ...
図解雑学ミクロ62頁参照
http://haginori55.jp/blog-entry-36.html
『ビューティフル・マインド』
2015年5月23日、ノーベル経済学賞受賞者で、映画『ビューティフル・マインド』の主人公であるジョン=ナッシュ氏(86)夫妻が交通事故で死亡した。
このニュースを聞いてから、この映画のことがずっと気になっていたのだが、ようやくwowowで放映したものを録画して見ることができた。
『ビューティフル・マインド』
2001年のアメリカ映画。アカデミー賞では、作品賞、監督賞、助演女優賞、脚色賞を受賞。主人公のナッシュ博士にラッセル=クロウ。
何をいまさら2001年の映画を、といわれてしまいそうだが、今まで、たいして映画を見てこなかったので、今になって、その埋め合わせをしているところなのです。
で、評価は★★★★★。面白かった。
(14年前の映画とはいえ、この映画については、ネタバレしてしまってはいけないと思うので、あらすじ付きの解説は避けたいと思います。
とはいえ、序盤の、金髪の美女がいるパーティーで、ナッシュがアダム=スミスの理論の否定を思いつく場面が気に入ってしまったので、それについて書いておきたいと思います。)
ナッシュは、金髪の美女をものにしたいと思うが、みんなが彼女を狙ってしまえば、競い合ってしまい、だれも彼女を獲得できず、みんなが不幸になると考える。
ではどうしたらいいのか?
そこから、アダム=スミスの理論の否定を思いつく。
アダム=スミスの自由放任論によれば、「競合社会では、個の野心が公の利益。」
みんなが競い合って豊かになろうとして経済活動を行えば、社会全体が豊かになる。
個々に利益を追い求めても、そこには「神の見えざる手」が働いて、うまくいくのさ、という理論。
しかし、これは、間違いだ!と、ナッシュは気づく。
「最良の結果は、グループ全員が自分の利益を追及すると得られる。」のではない!
「最良の結果は、全員が自分とグループ全体の利益を求めると得られる。」のだ!
経済活動の目的に「グループ全体の利益」という観点を持ってきたところが素晴らしい。
社会全体を良くするにはどうしたらよいか、という発想が根底にあるのだろう。
ジョン=ナッシュ。
ゲーム理論のうち、非協力ゲームの均衡分析の理論化で、ノーベル経済学賞を受賞。
うーん、何のことか、私の理解を越えてしまっていて、簡単な解説を読んでもよくわからなかったけれど、とにかく、すごい人だったのだな。
主演のラッセル=クロウは、この映画の前年の2000年には『グラディエーター』で、謀られてグラディエーター(剣奴)に身を落としてしまったローマの将軍マキシマスを演じた。この時は筋肉ムキムキの英雄。そして翌年のこの映画では、ちょっと猫背気味で、人付き合いが苦手で、天才数学者なのにどこか自信なさげで、弱々しい雰囲気のナッシュを演じている。うまくて感心した。
途中の展開は、予想外。
そしてラスト。
ありきたりの結びになってしまうけれど、ナッシュ博士を支えた妻のアリシアさんの心、およびこの2人の夫婦愛がビューティフルなのだと、当初、うさんくさいタイトルだなと思ったものの、納得。
見終わった後、気分が良かった。
2015-07-08 世界史 Comment:0 Trackback:0
ゲーム理論入門/(7)映画「ビューティフル・マインド」について - himaginaryの日記
http://d.hatena.ne.jp/himaginary/20080826/game_7
ゲーム理論入門/(7)映画「ビューティフル・マインド」についてAdd Star
経済, 映画 |
映画「ビューティフル・マインド」について
ナッシュの半生を描いた映画「ビューティフル・マインド」では、ナッシュがナッシュ均衡のアイディアを思いつくシーンで、以下のようなシチュエーションが描写されている。
1人の美人とそれ以外の女性3人がバーに入ってくる
こちらの男性は3人
→ 3人が1人の美人に群がれば、競合して誰も美人をゲットできないだけでなく、気を悪くした他の3人の女性にも相手にされなくなる。結局、誰も女性をゲットできない。
→ 3人が美人を無視してそれぞれ美人以外の女性にアタックすれば、各人が女性をゲットできる。こちらの方が皆がハッピーな結果となる。
映画では、この考察をもとに、バーを飛び出したナッシュが後にノーベル経済学賞の対象となる論文を書いたことになっている。
しかし…
他者が美人を無視するならば、自分が美人をアタックするのが最適反応戦略となる。すなわち、映画のナッシュが良いと考えた結果はナッシュ均衡ではない。
ゲーム理論では全体にとって良いかどうかを考えて行動する利他主義は想定していない。それは、ナッシュ均衡は必ずしもパレート最適とならないことに端的に表れている。
ハリウッドの脚本だから仕方ないのかもしれないが、これではナッシュ均衡に関する誤った理解が広がる恐れがある!
(…でもこの脚本が第74回アカデミー脚色賞を取っている)*1
ビューティフル・マインド [DVD]
ビューティフル・マインド [DVD]
出版社/メーカー: 角川エンタテインメント
発売日: 2008/10/17
メディア: DVD
購入: 1人 クリック: 61回
この商品を含むブログ (22件) を見る
ちなみに、「Anderson, Simon P., Maxim Engersy (2002) “A Beautiful Blonde: a Nash coordination game,” University of Virginia, Working Paper」(リンク)では、このシチュエーションのナッシュ均衡について考察を行っている。
*1:個人的な話をすると、当初はこの映画を公開時に見に行こうと考えていたのだが、「王様のブランチ」などの紹介番組でこのシーンを見て一気に行く気を失った。ナッシュ本人も含めこの点をあまり気にした人はいなかったようだが、これではニュートンがリンゴが木から落ちるのを見て天動説を考え付いた、とか、アインシュタインがニュートン力学の限界に気づいてエーテル理論を思いついた、というのと同じようなものではないか、と一人で非常に憤激していたことを覚えている。
当時の私の友人に宛てたメールから、そのあたりの失望感が現れている部分を引用しておく:
=======
先ほどTBSの「王様のブランチ」で「ビューティフル・マインド」(日本では本日公開)のそのシーンをやっていましたが、これって「他人の戦略を所与とした場合の最適反応戦略を各人が取っている」という定義からして、ナッシュ均衡になっていないのではないでせうか。(他人が美人をあきらめるという戦略を所与とすれば、自分が美人を口説くのが最適戦略になる) ま、脚本家が勝手に創り上げたエピソードだからどうでも良いけど。 [Sent: Saturday, March 30, 2002 11:59 AM]
=======
その後CSN1の映画紹介番組でそのシーンをもっと詳しくやっていましたが、その中では「アダム・スミスは間違っている。自分の利益だけじゃなく全体の利益も考えなくてはならないんだあ~」と叫びつつナッシュが酒場を出て行くシーンが紹介されていました。これはむしろゲーム理論ではなく厚生経済学の考え方だと思いますが、ひょっとしてこれは、ナッシュが狂気の中で自分が19世紀のイタリア人経済学者Paretoになったと錯覚して、パレート均衡(誰も他人の効用を悪化させずに自分の効用を高めることができない状態)の概念を思い付いたという幻想を再現したシーンなのでせうか…てそんなわけないか(でもこれでアカデミー脚色賞もらっているんだからな~)。 [Sent: Saturday, March 30, 2002 07:34 PM]
=======
2011(2006)
ゲーム理論
版情報 新版
著者名等 岡田章/著 ≪再検索≫
著者等紹介 1954年和歌山県生まれ。77年東京工業大学理学部卒。82年同大学院総合理工学研
究科博士課程修了、同大学理学部情報科学科助手。89年埼玉大学大学院政策科学研究科
講師、助教授、96年京都大学経済研究所教授等を経て、2004年より一橋大学大学院
経済学研究科教授。
出版者 有斐閣
出版年 2011.11
大きさ等 22cm 485p
NDC分類 331.19
件名 ゲーム理論 ≪再検索≫
要旨 新たに「進化ゲーム」の章を加え、さらに各章では、ドル・オークション、戦略的な情報
伝達、評判と不完全情報、電子メール・ゲーム、グローバル・ゲーム、金融政策の時間非
整合性、不完備契約、ネットワーク形成、協力の進化など、応用トピックの解説を大幅に
追加しさらにパワーアップ!最終章「ゲーム理論のフロンティア」では行動ゲーム理論や
確率進化ゲーム理論、学習の理論など最新の動向も解説。
目次 ゲーム理論とは何か;戦略形ゲーム;展開形ゲーム;完全均衡点;情報不完備ゲーム;繰
り返しゲーム;期待効用理論;交渉ゲーム;コアの理論;他の協力ゲーム解;進化ゲーム
;ゲーム理論のフロンティア
内容 長く信頼と好評を得ている決定版テキストが、最新理論をふまえてパワーアップ。進化ゲ
ームの章を設け、基本トピックの解説、90年代後半から現在に至るまでの重要な研究成
果や、様々な応用例を各章に盛り込んだ。
ISBN等 4-641-16382-0
ISBN等 978-4-641-16382-9
書誌番号 3-0211084765
所蔵情報 ( 資料情報 | 予約情報 )
項番 資料番号 所蔵館 請求分類 取扱 状態 場所 年月日号
1 2047358992 中央 331.1 / 可 貸出中 4階(社会科学)
2 2047370119 南 331 / 可 書架 公開
3 2047433315 保土谷 331 / 可 書架 公開
4 2049130247 山内 331 / 可 書架 公開
5 2047386937 都筑 331 / 可 書架 公開
6 2047517039 戸塚 331 / 可 書架 公開
トラクリ
Saussure in fact employed a model of political economy when he considered language as a synchronic system (i.e., Langue). The concept cept "synchronic" indicates a certain state of equilibrium rather than a tentative instant in time. The conventional linguistics had focused on observing a certain linguistic element in its historical transformation, tion, as detached from the whole of the system. Saussure posed an antithesis to it: The transformation of elements in a relational system tem provokes a shift of the whole system and produces a new system; the diachronic transformation of a language must be grasped as a change of system itself. This is nothing short of a shift from one equilibrium to another. This idea was obviously taken from "the general eral equilibrium system" of Vilfredo Pareto (1848-1923), who was teaching at the University of Laussane. But Saussure further developed oped this framework; he did not remain in Pareto's model, like many of Jakobson's examples, which were just rewordings of neoclassical economics. Saussure differentiated himself from neoclassical theory. His conviction viction was that in language there are only differences; it is a system of pure value"-these statements could not have been said had he thought within a unitary system (i.e., of a Langue). He introduced the concept of value only when he took into consideration another system of Langue. Saussure's point is that when a word is translated into another language, it achieves the same meaning, yet at the same time, the value of the word is altered in the new/different system in correspondence to its different relationship with other words. From this focal point, he explains that there is no meaning (the signified) that is apodictically tied to the signifier, in other words, no immanent meaning. As Hjelmslev pointed out, the signifier fier and the signified cannot be conceptually separated as long as one synchronic system is concerned. The concept of value as distinct from meaning-or `price', in economics-becomes necessary only when manifold/different systems are at stake. What about Marx? In general terms, he negated the idea of seeing money and language analogically. "To compare money with language guage is no less incorrect. Ideas are not transformed into language in such a way that their particular attributes are dissolved and their social character exists alongside them in language as do prices alongside commodities. Ideas do not exist apart from language. Ideas which must first be translated from their mother tongue into a foreign language in order to circulate and to become exchangeable would provide a better analogy; but then the analogy is not with the language but with its foreignness."" That is to say that, if an analogy between language and money becomes crucial at all, it is only where their foreignness [Fremdheit] is at stake. Saussure employed economic figures only when he spoke of the value of language that is distinguished from meaning. He explained it by using examples of different currencies.13 If one follows this analogy, meaning is identified with price, while value corresponds to the difference between the relational systems that determine price. Within a synchronic system, a commodity is made to be related to all other commodities. Exchanging a commodity with money is not simply ply an occurrence between two things (the
トラクリ
ソシュールは実際、言語を同期システム(つまり、ラング)と見なしたときに政治経済のモデルを採用しました。 「同期」という概念は、一時的な瞬間ではなく、一定の平衡状態を示します。従来の言語学は、システム全体から切り離された、その歴史的変化である特定の言語要素を観察することに焦点を合わせていました。ソシュールはそれに対してアンチテーゼを提示した。関係システムの要素における要素の変換は、システム全体のシフトを引き起こし、新しいシステムを生み出す。言語の通時的変換は、システム自体の変化として把握する必要があります。これは、ある平衡状態から別の平衡状態への移行にほかなりません。この考えは明らかに、ローザンヌ大学で教えていたヴィルフレード・パレート(1848-1923)の「一般的な一般均衡システム」から取られました。しかし、ソシュールはさらにこのフレームワークを開発しました。彼は、新古典派経済学の単なる言い換えであった多くのヤコブソンの例のように、パレートのモデルに留まっていませんでした。ソシュールは新古典派理論との差別化を図った。彼の有罪判決は、言語には違いしかないというものでした。それは純粋な価値のシステムです」-これらの声明は、単一のシステム(つまり、ラングのシステム)内で考えていたとは言えませんでした。彼は、ラングの別のシステムを考慮したときにのみ価値の概念を導入しました。単語が別の言語に翻訳されると、同じ意味を達成しますが、同時に、その単語の値は、他の単語との異なる関係に応じて、新しい/異なるシステムで変更されます。 、彼は、シグニファイヤーに黙示的に結び付けられている意味(記号化された)はない、言い換えれば、内在的な意味がないことを説明します。Hjelmslevが指摘したように、意味や経済学における「価格」とは異なる価値という概念は、多様なシステムが危険にさらされている場合にのみ必要になります。類推的に言語。 「お金と言語ゲージを比較することも間違いではありません。アイデアは、特定の属性が解消され、商品と並んで価格がそうであるように、言語にソーシャルキャラクターが存在するような方法で言語に変換されません。言語以外のアイデアは存在しません。 。最初に母国語から外国語に翻訳して交換可能にする必要があるアイデアは、より良い類似性を提供しますが、その類似性は言語ではなく、その外国語です。」言葉とお金の類推がまったく重要になれば、それは彼らの外国性[Fremdheit]が危機にatしているところでのみです。ソシュールは意味と区別される言語の価値について語ったときにのみ経済図を使用しました。異なる通貨の例。13この類推に従うと、意味は価格で識別され、価値は関係システム間の差に対応するt価格を決定します。同期システム内では、商品は他のすべての商品に関連付けられます。商品をお金と交換することは、2つの事柄の間の単なる発生ではありません(
2020/3
群像
マルクス可能性
序文では
トラクリと違い
ワルラスからソシュールの間にパレートの名がないから分かりにくい
コメントを投稿
<< Home