NAMs出版プロジェクト: 正方形と同じ面積の正三角形の作図

正三角形の一辺を２ｘとし、ｘ＝１とすると、

√３の面積の正三角形が出来る。同面積の正方形を作ると、

その正方形の一辺は√√３。

以下参考：

正方形と同じ面積の正三角形の作図
http://www.geocities.jp/ha415713/tex/touseki.pdf

3/3

http://www004.upp.so-net.ne.jp/s_honma/mathbun/mathbun162.htm

・　正方形から正三角形　　　　　　　　　　　　　Ｓ．Ｈ氏

　正方形をいくつかの部品に分解して正三角形を作る問題は多々ある。しかし、分割された
部品が互いに連結されたまま移動することによって正三角形（または正方形）ができること
に感動した。

　これは、数学者の秋山　仁先生が以前ＴＶで実演されていた。このアイデアを用いた家具
も作られていた。

　まず、下図のように正方形を分割する。（詳細は後述）

　　　　　　　

　その分割された部品に対して、下図のように連結部分（青い点）を設ける。

　　　　　　　

　その連結部分を中心として、各部品を回転させる。

　　　　　　　

　そうすると、下図のような正三角形が作られる。

　　　　　　

　それでは、正方形をどのように分割したら、このような正三角形が作られるのだろうか？
闇雲に分割しても、それは失敗するばかりである。次のように考えればよい。

　　正三角形ＡＢＣの頂点Ａを通り、長さがＢＣに
　等しく、ＢＣに平行な線分ＤＥをとる。

　　線分ＢＥの垂直２等分線と線分ＢＥの交点を
　Ｆとする。

　　この垂直２等分線と線分ＥＦの長さを基にし
　て正方形ＧＨＩＪの４頂点が定められる。
　
　　左図では、点Ａは線分ＤＥの中点として作図
　したが、Ａの位置をずらすことによって、いろい
　ろな造形の変化を楽しむことが出来るだろう。

　上図から、「正方形と同じ面積を持つ正三角形が作れる」ことは明らかだろう。

　特に、点Ａが線分ＤＥの中点とした場合を考える。

　始めに与えられる正方形ＧＨＩＪの１辺の長さを２とすると、作図の解析から、

　　　　　ＢＦ＝ＦＥ＝１

である。　このとき、正三角形ＡＢＣの１辺の長さをａとすると、

　　　　　（ａ/２）²＋（

ａ/４）²＝１

より、　ａ＝４

/７　となるので、この長さを１辺に持つ正三角形を作図すれば、上記のよ

うな手順で、面積４の正方形が作図され、さらに、正方形を上図のように切断すれば、正方

形と同じ面積を持つ正三角形を構成することが出来る。

　それでは、逆に、最初に正三角形を与える場合はどうだろうか？

　　　　　　　　　

　この場合も、上記と同様に、上図のように切り分ければ、面積の等しい正方形を作ること
ができる。

　この話題が、

北大数学科（編）　中村　郁（監修）
　　　　　　　　　　　　　　　　　　　北大高校生講座　　数学の並木道　（日本評論社）

の、ｐ１０～ｐ１２に取り上げられている。

参考：

■『数学マジック事典改訂版』98頁
http://www.fukkan.com/fk/CartSearchDetail?i_no=68324248&tr=s
――――――――――――――――――――――――――――――――――
【著者】上野富美夫
【発行】東京堂出版
【定価】2,052円（税込み）
【発送時期】2015/08/下旬

知的な興奮と刺激で頭を新鮮にする一冊！

マジックの中でも数学の仕組みを用いた基本的なものを網羅。愉しく覚え
ながら、数の不思議、面白さに触れられ数学入門にもなる一冊です。数学の
基礎も学べるロングセラーが図版・紙面も見やすく、解説も補足し、より
分かり易くなりました。
　
▼目次
Ⅰ 数を当てるマジック
Ⅱ 図形が変わるマジック
Ⅲ 高速暗算のマジック
Ⅳ 位相幾何学（トポロジー）のマジック
Ⅴ 暗号・通信のマジック
Ⅵ ゲーム必勝のマジック
Ⅶ 論理のマジック・パラドックス

このような図形の分割は、へンリー. E.デュードニー(Henry. E. Dudeney)

が1907年の著作 The Canterbury Puzzlesで発表したものである。

『カンタベリー・パズル』伴田良輔訳、筑摩書房〈ちくま学芸文庫テ7-1. Math & science〉、2009年3月。ISBN 978-4-480-09203-8。232頁(62頁)参照。

26.小間物行商人のパズル

次ぺージの図のように，正三角形の布を4つに切断すれば正方形に組み替えることができる.

　線分ABを点Dで二等分し，線分BCを点Eで二等分する.線分AEの延長線上にEB=EFとなる点Fをと

る．線分AFを点Gで二等分し，弧AHFを描く.線分EBを点Hまで延長すると，線分EHは求める正方形のー

辺の長さに等しい．点EからEHの距離で弧HJを描き，BE=JKとなる点Kをとる，こんどは点Dと点Kから線

分EJへ垂線を下ろし，交点をそれぞれ LとMとする. 以上を正確に行えぱ，解の方針を得られるだろう.

デュードニー分割のつくりかた

http://www20.big.or.jp/~morm-e/puzzle/column/003/003.html

ーーーー

√3を1.732...と導き出す方法を教えてください awa0waさん 2015/01/02

√3を1.732...と導き出す方法を教えてください

ベストアンサー budewslakothさん 2015/01/02

1/2(1.7+3/1.7)=1.732....

いろいろあります。

①漸化式
√3
(3/1 +1)/2=2
(3/2 +2)/2=1.75
(3/1.75 +1.75)/2=1.73…
(3/1.73… +1.73…)/2=1.73…

②級数展開
√3=2√0.75=2∑[n=0,∞]((-1)^n (2n)! (0.75-1)^n)/(4^n (n!)^2 (1-2n))
=2(1+(-0.25)/2 -((-0.25)^2)/8+((-0.25)^3)/16-(5(-0.25)^4)/128+…)

③連分数
√3=1+(√3 -1)
=1+(3-1)+(3-1)/(2(3-1)+(3-1)/(2(3-1)+(3-1)/(2(3-1)+…)))))
=1+2/(2+2/(2+2/(2+2/(2+2/(2+2/(2+2/(2+2/(2+2/(2+…)))))))))

④無限乗積展開
√3=2×((6の倍数-3±1)÷(6の倍数-3))×…
=2×(2/3)×(4/3)×(8/9)×(10/9)×(14/15)×(16/15)…

⑤開平法
知恵袋では筆算の表現が難しいので
↓サイトを参考にしてください。
http://dic.nicovideo.jp/a/%E9%96%8B%E5%B9%B3%E6%B3%95

http://izumi-math.jp/F_Nakamura/kaihei/kaihei.htm
melancholycorisさん
2015/01/02 11:46:36

a_1=2 で、a_(n+1)=((a_n)^2 +3)/2a_n という漸化式を考えると、

a_nはかなり早いスピードで√3に近づいていきます。

2 7/4 97/56 ・・となりますが第三項ですでに1.73214...です。

詳しくは「ニュートン法」と検索してみてください。

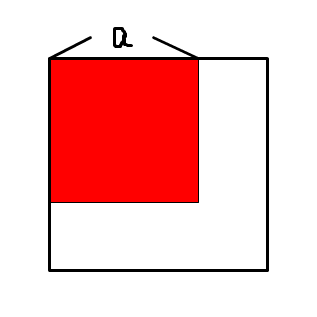
http://dic.nicovideo.jp/t/a/%E9%96%8B%E5%B9%B3%E6%B3%95

平方根を求めるのは、図形的に言うと、面積のわかっている正方形から1辺の長さを求めることと同じである。開平法は、正方形の1辺の長さを求めるために、少し小さい正方形を用いて近似していくのである。ここでは、元の正方形の面積をSとする。筆算では次のように書く。


√S

準備段階では、桁数を決めている。平方根の桁数は、元の数を2桁ずつ区切ったときの数と一致している。

第1ステップでは、最も上の位で近似する。前述の例では、10単位で近似している。ここでは、近似する正方形の1辺の長さをaとする。図に表すと次のようになる。

aの値は、赤い正方形の面積が全体の正方形を超えないような最大のものである。前述の例で言えばa = 10である。さて、筆算ではどのようになるか。aを立てて計算すると次のようになる。

a
a
2a 　 a
√S
   a²
   S-a²

左側はaを2倍しているので、赤い正方形の1辺の長さの2倍、右側では全体の正方形から赤い正方形の面積を引いているので、白い部分の面積が求められる。左側は第1ステップでは特に意味がないが、次のステップで使われることになる。

第2ステップは、単位を1桁下げて近似する。前述の例では1単位で近似している。このとき、近似する正方形の1辺の長さの、前のステップから増分をbとする。図で表すと次の通り。

bの値は、青い部分の面積が赤くない部分を超えないような最大のものである。青い部分の面積を式で表すと、2ab+b²となる。bで括ると(2a+b)×bとなり、これは前述の例で言うところの2□×□となる。結果として5が立つ。bを使って筆算を進めると、次のとおり。

a
a
2a+b
      b
2a+2b = 2(a+b) 　 a + b
√S
   a²
   S-a²   2ab+b²
   S-a²-2ab-b² = S-(a+b)²

まず左側では青い部分も含めた正方形の1辺の長さの2倍が出る。これは次のステップに使われる。右側では青い部分の面積を引いているので、残りの白い部分の面積が求められる。左側のおかげで青い部分の面積が容易に計算できるのがおわかりだろうか。

第3ステップ以降も第2ステップとやってる事は同じ。近似する単位を1桁下げ、左側を使って増分を計算し、右側から引くことで残りの面積を計算している。

ーーー

ルートを開こう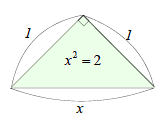

　無理数である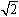の値は近似式で求められます。あるいは手元に電卓があるのなら、ちょっと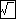キーを叩いてみれば済むことです。ただ、近似式は小数第何位かで狂いが生じ、また電卓はディスプレイの表示桁数に限界があります。
　しかし開平法(平方根を求める方法)では、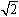に限りなく近い値を求めることが可能なのです。
例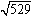　を開平してみましょう。
　　　529=(10a+b)²=100a²+20ab+b²
とみると、10²＜529＜10⁴ですから、529は2桁の数です。そこで一の位が0である2桁の数の平方で529に一番近い数を求めると、20が得られます。次に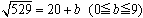とおき、両辺を平方します。529=400+40b+b²よりb=3が分かり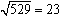となり開平できました。
問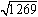　を開平してください。
　では、この計算の仕組みを考えてみましょう。
　2桁の整数xは、x=10a+b（1≦a≦9，0≦b≦9）と表せます。
　　　x²=100a²+20ab+b² より、
　　　x²-(10a)²=(20a+b)b
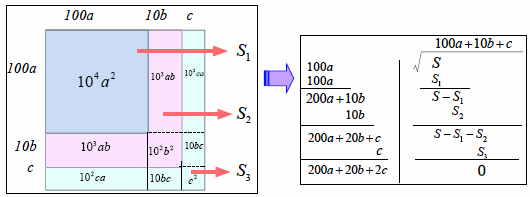
　これは、図のようにx²を面積とみると、おおざっぱに十の位の数の平方を表す面積100a²を求めて、残りの面積から1の位の数を算出していることが分かります。
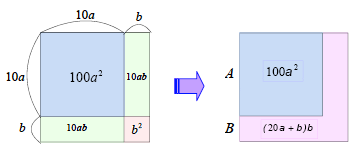
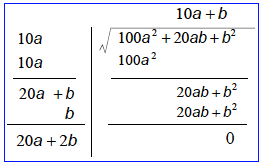　この計算を簡略化すると次のようになります。
　計算は2つのブロックに分かれています。左側は平方根の各位の数を求めている部分であり、右側は平方数の表している面積と、残りの面積を計算する部分です。
例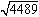　の開平で実際の計算の流れをみてみましょう。
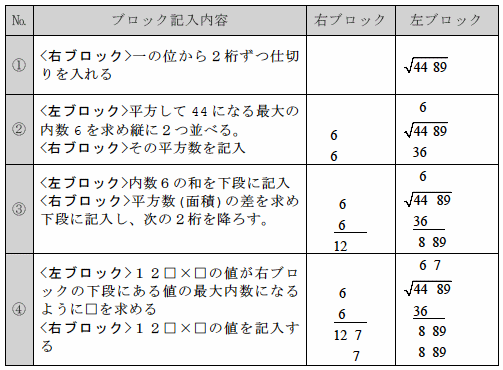
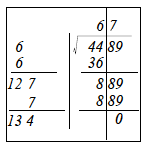　以下同様に計算し、右ブロックの面積の差が0になる（開ききる）まで続けます。
問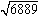　を開平してください。
問　開平した値が3桁の場合でも同様の計算ができることを図で確認し、次の数を開平してください。
　(1)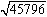　　(2)
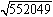
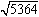例　を開平してみましょう。
　右がその計算結果ですが、面積が残ってしまいました(この面積を開平の残りといいます)。これは、
　　　5634=73²+35
となることを意味します。
　そこで、さらに同様の手順で計算すると次のようになります。
　　　5634=73.2²+5.76
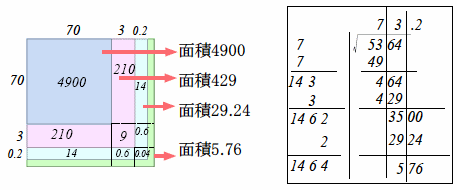
となり、小数第1位まで平方根が開かれました。このように、開平計算では、おおざっぱに10²の幅で平方数の表す面積を近似することによって、百の位、十の位、一の位、小数点第１位と値を絞っていくことができます。
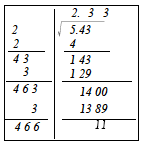例　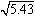を小数第2位まで計算してみよう。
問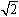　を小数第6位まで計算してください。

ーーー

ニュートン法 - Wikipedia
https://ja.wikipedia.org/wiki/%E3%83%8B%E3%83%A5%E3%83%BC%E3%83%88%E3%83%B3%E6%B3%95

ニュートン法の一手順の概念図 (青い線が関数 f のグラフで、その接線を赤で示した). x_n よりも x_n+1のほうが、 f(x)=0 の解 x についてのよりよい近似を与えている.

この方法の考え方は以下のようである：まず初めに、予想される真の解に近いと思われる値をひとつとる。次に、そこでグラフの接線を考え、その x 切片を計算する。このx切片の値は、予想される真の解により近いものとなるのが一般である。以後、この値に対してそこでグラフの接線を考え、同じ操作を繰り返していく。

上の考え方は次のように定式化される。ここでは、考える問題を f: R → R, x ∈ Rとして

$f(x) = 0\,$

となる x を求めることに限定する。このとき、x の付近に適当な値 x₀ をとり、次の漸化式によって、x に収束する数列を得ることができる場合が多い。

$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \quad \cdots (1)$

例として、√2 を計算で求める場合に、

$f(x) = x^2 - 2\,$

とおき、f(x) = 0 の解を求めることを考える。

$f'(x) = 2x\,$

であるので、(1) の式は

$x_{n+1} = x_n - \frac{x_n^2-2}{2x_n}$

と書き表せる。たとえば x₀ = 1 とおくと、この数列は √2 に収束し、x₀ = -1 とおくと、この数列は -√2 に収束する。

NAMs出版プロジェクト

火曜日, 9月 01, 2015

正方形と同じ面積の正三角形の作図

0 Comments:

Previous Posts