ラグランジュの未定乗数法 - Wikipedia
無差別曲線の限界と関係する。
無差別曲線とは何か | 永井俊哉ドットコム
https://www.nagaitoshiya.com/ja/2002/3d-indifference-curve/
ラグランジュの未定乗数法 - Wikipedia
https://ja.wikipedia.org/wiki/%E3%83%A9%E3%82%B0%E3%83%A9%E3%83%B3%E3%82%B8%E3%83%A5%E3%81%AE%E6%9C%AA%E5%AE%9A%E4%B9%97%E6%95%B0%E6%B3%95ラグランジュの未定乗数法(ラグランジュのみていじょうすうほう、英: method of Lagrange multiplier)とは、束縛条件のもとで最適化を行うための数学(解析学)的な方法である。いくつかの変数に対して、いくつかの関数の値を固定するという束縛条件のもとで、別のある1つの関数の極値を求めるという問題を考える。各束縛条件に対して定数(未定乗数、Lagrange multiplier)を用意し、これらを係数とする線形結合を新しい関数(未定乗数も新たな変数とする)として考えることで、束縛問題を普通の極値問題として解くことができる方法である。
幾何学的な説明
簡単のため2次元の場合を考えよう。g (x,y ) = c(ここでc は与えられた定数である)に対し、関数f (x,y ) を最大化するものとしよう。f の値を高さとしたグラフを考える。d のいろいろな値に対しf (x,y ) = d で与えられるf の軌道が考えられる。束縛条件はg の値をc に固定してg が1つの軌道にあるとすることである。g =c の軌道に沿って歩くと、f とg の軌道は違うから、この軌道は一般に多数のf 軌道を横切ることになる。そこでd の異なる値に対して横切るいろいろなf =d の軌道に注目しよう。軌道を横切るとすると、坂を上ればf の値は増加する(下れば減少する)。
ただし横切ろうとしている軌道f =d が実際は軌道g=c(束縛条件)と交差せず接触だけする場合に限り、f の値は変化しない(束縛条件下でf が最大となる点ではまさにそうである)。ここではf とg との勾配ベクトル(各変数による偏微分を成分とする)の向きが同じになる。
ここで0でないスカラー λ を導入し、f − λg を考える。上の点の条件は、λ のある値に対してf − λg の勾配が0であるということに等しい(λ はfとg の勾配の比)。





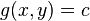 を示す。青い線は
を示す。青い線は の等高線。赤い線が青い等高線に接する点が解。
の等高線。赤い線が青い等高線に接する点が解。
0 Comments:
コメントを投稿
<< Home