( 経済学、リンク::::::::::)
参考:
経済数学の直観的方法 確率・統計編 (ブルーバックス)/長沼伸一郎
http://nam-students.blogspot.jp/2016/12/honto.html
ブラックショールズ:熱伝導方程式 https://youtu.be/F_8XjAzUNxA
http://nam-students.blogspot.jp/2016/07/httpsyoutubef8xjazunxa.html @
ブラックショールズ;熱伝導方程式
https://youtu.be/F_8XjAzUNxA
ブラウン運動を表す
https://www.youtube.com/channel/UC_wqdU_Igw6NcmDamOGeHew/videos?view=0&sort=dd&shelf_id=0
以前の記事でブラック・ショールズ方程式(BS方程式)の前置きとして
オプションの説明をしました。(参照:オプション取引って、賭博?)
今回は本題に入ります。
数学の話題なので、専門用語も多少使いますが勘弁してください。
クオンツを目指す方に、
専攻が金融でなくても、
時間がなくても、
お金がなくても(文庫本なので高くない)
最低限押さえるべき知識が得られると思うので
木島正明『金融工学』(日経文庫)
をお薦めしておきます。
別の記事に書くけど、面接で問われるのは知識じゃない。
たまたま知っていることに左右されるような面接は向こうも望まない。
だから、基本を深く考えていった方が有効だと思う。
ということでこの文庫本を侮るなかれ。
文庫本なのにちょっとした専門書くらいの内容があります。
まず、
ブラック・ショールズ方程式の意義みたいなとこを書いておくと、
オプション価格を算定する方法を初めて与えた
ということだけでも十分に価値があるんだろうけど、
・リスクプレミアム(価格変動に対する対価)
の概念や、
「同一のキャッシュフローを生成する金融資産の現在価値は等しい」
という
・一物一価の原理
をみごとに応用して、その後のパラダイム(指導原理)を示した
というところにノーベル賞でも報いられた功績があるんだろうと思う。
そして1973年以降、これを応用して債権だろうがワラントだろうが、
様々な金融派生商品の計算ができるようになったのです。
だから、金融工学の原点か代名詞みたいに言われたりするのですね。
ブラック・ショールズの公式と呼ばれるものもありますが、
こちらはブラック・ショールズ方程式の特殊な場合の解です。
ブラック・ショールズの公式は、
価格変動率が時間で変動しない、など
いくつもの仮定をおいているために「不自然だ」と
批判の対象にもなるのだけど、
科学というのは捨象と一般化の葛藤に取り組むものでもあるのだから、
そういった批判はちょっと論点がずれている気がする。
金融取引はリアルタイムでばんばん進行するわけで、
実用の範囲で理論が使えなければ意味がない。
実用的かどうかはコンピューターの性能との兼ね合いでもあるので、
計算機の発達や金融商品の複雑化の過程で、
ブラック・ショールズ方程式は必然的に生まれたとも言える。
それ以後革新的な進展はない、
という話まであるのはちょっと困ったものだけど。
そして、特殊な場合の解であっても簡単な形で提示してある
ブラック・ショールズの公式は今でも現場の便利なツールなのだそうだ。
(注…ブラック・ショールズ方程式の方はもっと一般的に応用できます。)
ところで、この方程式は導出の過程に伊藤清によって発見された
「伊藤の公式」という確率解析の成果を利用しています。
リスクプレミアムの簡単な等式を
伊藤の公式に代入するだけで驚くほど簡単に
ブラック・ショールズ方程式が得られます。(上記の本にあります)
(これだけでも伊藤清の仕事の重要性が分かるかと思いますが、
こういう感じで特に戦後しばらくの時期の
日本人数学者・物理学者の活躍には大変なものがあるのですよ。)
確率解析、確率微分方程式は
僕もですがあんまり馴染みがない人が多いと思いますが、
この結果だけ押さえておけばそれほど困らないようです。
ブラック・ショールズ方程式はただの微分方程式ですから。
***
以下では、
ブラック・ショールズ方程式の解法について書こうと思ったんだけど、
よい解説を見つけたのでそちらを引用して
解法については簡単に触れるだけにします。
ブラック・ショールズ方程式は、

C(t,S): オプション価格の関数、
t: 時間、
S: 原資産価格、
r: 無リスク資産の利子、
σ: 資産価値の変動率、
で与えられます。
この方程式は一般的には解けないので、
σとr → 定数、
という近似をして得られるのが
ブラック・ショールズの公式です。
つまり、
ある時点の時間と原資産価格(株など)をインプットすれば、
その時のオプション価格Cが求めることができるということです。
ここでは、単純なコール・オプションを想定し、
オプション価格の境界条件(満期での最終価格)は、
満期(t=T)で
C(T,S) = max(S-K, 0)
K: オプションの行使価格
を考えてみます。
記号で書きましたが、この式は、
「満期のオプション価格Cは、
0円か、権利を行使して得る額S-K円の大きい方に等しい」
と文章で書いても全く同じことです。
グラフだと、下の赤い線に対応します。
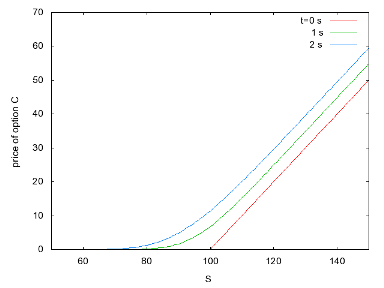
このオプションを持っていたら、
満期で原資産SがK=100円以上に値上がりしたら差額が儲かる、
SがK=100円より安かったら何も得られない。
満期ではもはや資産は変動しないですから、
オプションが生み出すキャッシュフローが
そのまま満期でのオプションの価格になる、というのは自然ですね。
目標は、任意の時点でのオプション価格を計算することです。
この方程式を解くための方針は、
A.ブラック・ショールズ方程式を変数変換で熱伝導方程式に変える。
B.熱伝導方程式の一般解に(変換を考慮した)境界条件を代入する。
C.変数を元に戻す。
だけです。
次の

なんて変換を行えば一発で熱伝導方程式になるのですが、
こんな変形は急に思いつくものでもないし
意味が不明瞭なので3段階でやってみます。
各項で「S微分の次数」と「係数のSの次数」が等しい、
ということに気づくと
① S = (定数)× e^y (eのy乗), τ= T-t 変数:yとτ
の変換で線形微分方程式にできます。
② x = y + (r - σ^2/2)τ, l = τ 変数:xとl
で、の一次の微分の項を消し、
③ Q = C e^(rl)
の置き換えで微分のない項も消すと
めでたく熱伝導方程式(または拡散方程式)

を得ます。
②’Q = C e^(ay + bτ), (a,bはある定数)
という変換で2段階で変換する方が簡単かなと思ったんだけど、
あとで初期条件が面倒になるので上記やり方がベターでした。
ここまでくると、変数変換に気をつけながら
あとは熱伝導方程式の境界問題を解けばいいわけですが、
詳しくは
http://www1.parkcity.ne.jp/yone/finan/Finan06_07.htm
でも参照してください。
(ただし、この解説は第4、5段階のところで、
初期条件からのSが積分内ではmの、外ではxの関数であるのを
見落としていて、その計算が間違っているので注意。)
最終的にブラック・ショールズの公式
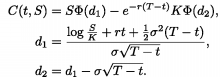
が得られます。
ここでΦはガウス積分あるいは誤差関数です。
その他に、
・リスク中立化法
・二項モデルの連続極限
などの方法でもブラック・ショールズの公式を得ることができます。
二項モデルについてもそのうち考えてみたいです。
***
今回はブラック・ショールズ方程式の解き方について
コメントしましたが(何もやってない?)、
長くなったので次回に続きます。
後編では、今回の結果と熱伝導方程式を使って
ブラック・ショールズ方程式の解をイメージする方法
を説明する予定です。
ところで、
就職に向けて何を勉強したらよいですか?と未来のボスに尋ねたところ
「クオンツバカにならないために」、と
以下の本も薦めてくれました。
『金融技術革命未だ成らず』
面白そうですね。
では。
今度は、100円を中心に山が崩れていくのが観察できます。
熱伝導方程式の場合にそっくりですね!
さっき割引率の部分で触れましたが、
この中心のずれは時間を遡ると原資産価格Sを低めに取らないと
同じ価値にならないということが主要因だと理解できます。
(教育方針 - 考える道筋の視覚化
http://namihirahp.web.fc2.com/contents.html)
http://namihirahp.web.fc2.com/contents.html)
BS方程式の解き方|海外ポスドクの就職活動日記
http://ameblo.jp/gogo-pd/entry-10421794663.html
http://ameblo.jp/gogo-pd/entry-10421794663.html
以前の記事でブラック・ショールズ方程式(BS方程式)の前置きとして
オプションの説明をしました。(参照:オプション取引って、賭博?)
今回は本題に入ります。
数学の話題なので、専門用語も多少使いますが勘弁してください。
クオンツを目指す方に、
専攻が金融でなくても、
時間がなくても、
お金がなくても(文庫本なので高くない)
最低限押さえるべき知識が得られると思うので
木島正明『金融工学』(日経文庫)
をお薦めしておきます。
別の記事に書くけど、面接で問われるのは知識じゃない。
たまたま知っていることに左右されるような面接は向こうも望まない。
だから、基本を深く考えていった方が有効だと思う。
ということでこの文庫本を侮るなかれ。
文庫本なのにちょっとした専門書くらいの内容があります。
まず、
ブラック・ショールズ方程式の意義みたいなとこを書いておくと、
オプション価格を算定する方法を初めて与えた
ということだけでも十分に価値があるんだろうけど、
・リスクプレミアム(価格変動に対する対価)
の概念や、
「同一のキャッシュフローを生成する金融資産の現在価値は等しい」
という
・一物一価の原理
をみごとに応用して、その後のパラダイム(指導原理)を示した
というところにノーベル賞でも報いられた功績があるんだろうと思う。
そして1973年以降、これを応用して債権だろうがワラントだろうが、
様々な金融派生商品の計算ができるようになったのです。
だから、金融工学の原点か代名詞みたいに言われたりするのですね。
ブラック・ショールズの公式と呼ばれるものもありますが、
こちらはブラック・ショールズ方程式の特殊な場合の解です。
ブラック・ショールズの公式は、
価格変動率が時間で変動しない、など
いくつもの仮定をおいているために「不自然だ」と
批判の対象にもなるのだけど、
科学というのは捨象と一般化の葛藤に取り組むものでもあるのだから、
そういった批判はちょっと論点がずれている気がする。
金融取引はリアルタイムでばんばん進行するわけで、
実用の範囲で理論が使えなければ意味がない。
実用的かどうかはコンピューターの性能との兼ね合いでもあるので、
計算機の発達や金融商品の複雑化の過程で、
ブラック・ショールズ方程式は必然的に生まれたとも言える。
それ以後革新的な進展はない、
という話まであるのはちょっと困ったものだけど。
そして、特殊な場合の解であっても簡単な形で提示してある
ブラック・ショールズの公式は今でも現場の便利なツールなのだそうだ。
(注…ブラック・ショールズ方程式の方はもっと一般的に応用できます。)
ところで、この方程式は導出の過程に伊藤清によって発見された
「伊藤の公式」という確率解析の成果を利用しています。
リスクプレミアムの簡単な等式を
伊藤の公式に代入するだけで驚くほど簡単に
ブラック・ショールズ方程式が得られます。(上記の本にあります)
(これだけでも伊藤清の仕事の重要性が分かるかと思いますが、
こういう感じで特に戦後しばらくの時期の
日本人数学者・物理学者の活躍には大変なものがあるのですよ。)
確率解析、確率微分方程式は
僕もですがあんまり馴染みがない人が多いと思いますが、
この結果だけ押さえておけばそれほど困らないようです。
ブラック・ショールズ方程式はただの微分方程式ですから。
***
以下では、
ブラック・ショールズ方程式の解法について書こうと思ったんだけど、
よい解説を見つけたのでそちらを引用して
解法については簡単に触れるだけにします。
ブラック・ショールズ方程式は、

C(t,S): オプション価格の関数、
t: 時間、
S: 原資産価格、
r: 無リスク資産の利子、
σ: 資産価値の変動率、
で与えられます。
この方程式は一般的には解けないので、
σとr → 定数、
という近似をして得られるのが
ブラック・ショールズの公式です。
つまり、
ある時点の時間と原資産価格(株など)をインプットすれば、
その時のオプション価格Cが求めることができるということです。
ここでは、単純なコール・オプションを想定し、
オプション価格の境界条件(満期での最終価格)は、
満期(t=T)で
C(T,S) = max(S-K, 0)
K: オプションの行使価格
を考えてみます。
記号で書きましたが、この式は、
「満期のオプション価格Cは、
0円か、権利を行使して得る額S-K円の大きい方に等しい」
と文章で書いても全く同じことです。
グラフだと、下の赤い線に対応します。

このオプションを持っていたら、
満期で原資産SがK=100円以上に値上がりしたら差額が儲かる、
SがK=100円より安かったら何も得られない。
満期ではもはや資産は変動しないですから、
オプションが生み出すキャッシュフローが
そのまま満期でのオプションの価格になる、というのは自然ですね。
目標は、任意の時点でのオプション価格を計算することです。
この方程式を解くための方針は、
A.ブラック・ショールズ方程式を変数変換で熱伝導方程式に変える。
B.熱伝導方程式の一般解に(変換を考慮した)境界条件を代入する。
C.変数を元に戻す。
だけです。
次の

なんて変換を行えば一発で熱伝導方程式になるのですが、
こんな変形は急に思いつくものでもないし
意味が不明瞭なので3段階でやってみます。
各項で「S微分の次数」と「係数のSの次数」が等しい、
ということに気づくと
① S = (定数)× e^y (eのy乗), τ= T-t 変数:yとτ
の変換で線形微分方程式にできます。
② x = y + (r - σ^2/2)τ, l = τ 変数:xとl
で、の一次の微分の項を消し、
③ Q = C e^(rl)
の置き換えで微分のない項も消すと
めでたく熱伝導方程式(または拡散方程式)

を得ます。
②’Q = C e^(ay + bτ), (a,bはある定数)
という変換で2段階で変換する方が簡単かなと思ったんだけど、
あとで初期条件が面倒になるので上記やり方がベターでした。
ここまでくると、変数変換に気をつけながら
あとは熱伝導方程式の境界問題を解けばいいわけですが、
詳しくは
http://www1.parkcity.ne.jp/yone/finan/Finan06_07.htm
でも参照してください。
(ただし、この解説は第4、5段階のところで、
初期条件からのSが積分内ではmの、外ではxの関数であるのを
見落としていて、その計算が間違っているので注意。)
最終的にブラック・ショールズの公式
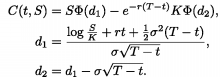
が得られます。
ここでΦはガウス積分あるいは誤差関数です。
その他に、
・リスク中立化法
・二項モデルの連続極限
などの方法でもブラック・ショールズの公式を得ることができます。
二項モデルについてもそのうち考えてみたいです。
***
今回はブラック・ショールズ方程式の解き方について
コメントしましたが(何もやってない?)、
長くなったので次回に続きます。
後編では、今回の結果と熱伝導方程式を使って
ブラック・ショールズ方程式の解をイメージする方法
を説明する予定です。
ところで、
就職に向けて何を勉強したらよいですか?と未来のボスに尋ねたところ
「クオンツバカにならないために」、と
以下の本も薦めてくれました。
『金融技術革命未だ成らず』
面白そうですね。
では。
BS方程式をイメージする方法|海外ポスドクの就職活動日記
http://ameblo.jp/gogo-pd/entry-10472502711.html
http://ameblo.jp/gogo-pd/entry-10472502711.html
今度は、100円を中心に山が崩れていくのが観察できます。
熱伝導方程式の場合にそっくりですね!
さっき割引率の部分で触れましたが、
この中心のずれは時間を遡ると原資産価格Sを低めに取らないと
同じ価値にならないということが主要因だと理解できます。
…







0 Comments:
コメントを投稿
<< Home