( 経済学、リンク::::::::::)
NAMs出版プロジェクト: 長沼伸一郎『経済数学の直観的方法 マクロ経済学編』:目次
http://nam-students.blogspot.jp/2016/09/blog-post_17.html
http://nam-students.blogspot.jp/2016/09/blog-post_17.html
長沼伸一郎「経済数学の直観的方法 マクロ経済学編」
https://itun.es/jp/xLw7eb.l ibooks
https://itun.es/jp/xLw7eb.l ibooks
経済数学の直観的方法 マクロ経済学編 (ブルーバックス) 電子書籍: 長沼伸一郎: Kindleストア
https://www.amazon.co.jp/dp/B01M1RFG08 kindle
https://www.amazon.co.jp/dp/B01M1RFG08 kindle
(ブルーバックス)2016/09/15(電子版09/23)
経済数学の直観的方法 確率・統計編 (ブルーバックス)/長沼伸一郎
http://nam-students.blogspot.jp/2016/12/honto.html
ブルーバックス電子版としては検索可、文字拡大可、しおり機能可など、仕様が改善されている。
ただし以下の記述における紙版の頁数が無意味になってしまった…。
ラムゼイモデルにこだわらない意味、ラムゼイモデルの特殊性(173,194頁)も参考になる。
オイラー方程式(161頁)が経済学と物理学では違う使われ方をするというのも面白い(165頁)。
制約条件(146,179頁)が大事になる。固有値(265,270頁)も本書で初めてイメージが掴めた。
第6章はミクロ経済学の基礎。
目次:
第1章 初級編
1.経済学は物理の思想からどう影響を受けて発達したか 18
2.「二大難解理論」以前のケインズ経済学 41
3.米国の経済思想と動的マクロ理論の登場 69
第2章 中級編 79頁~
1.フェルマーの原理に隠された動的理論の本質 80
2.「最速降下線」によるさらに高度な部分の理解 110
第3章 上級編 145頁~
1.動的マクロ理論の各モデル 146
2.各モデルの具体的内容 152
3.ラグランジュ乗数とハミルトニアンの関連性 207
第4章 経済学部で知っておくべき微分方程式の基本思想 229
第5章 固有値の意味 247
第6章 位相・関数解析 277
第1章 初級編
1.経済学は物理の思想からどう影響を受けて発達したか 18
2.「二大難解理論」以前のケインズ経済学 41
3.米国の経済思想と動的マクロ理論の登場 69
第2章 中級編 79頁~
1.フェルマーの原理に隠された動的理論の本質 80
2.「最速降下線」によるさらに高度な部分の理解 110
第3章 上級編 145頁~
1.動的マクロ理論の各モデル 146
2.各モデルの具体的内容 152
3.ラグランジュ乗数とハミルトニアンの関連性 207
第4章 経済学部で知っておくべき微分方程式の基本思想 229
第5章 固有値の意味 247
第6章 位相・関数解析 277
本書は物理数学の立場から経済動学へと至る段階を人類史的に四段ロケットのように分け、さらに経済動学自体を四段に分けている。前半(初級・中級編)の人類史的な部分が重要で、だからこそ上級編でもハミルトニアン(H)の基本思想である「このH(つまり全エネルギー)全体を常に一定に保っていく」(212~3頁)ことが「持続可能な経済」への可能性(226頁)を開くというような大胆な提言が出来るのだろう。
I「オイラー方程式」(159,163頁)
II 「制約条件」(178,180頁)
III「ラグランジュ乗数」(207頁)
この3つの原理が全編の鍵になる(146頁)。
フェルマーの原理*を最初の動学の基本に据えた部分がオリジナルな発想だ。固有値やポントリャーギン理論の説明もわかりやすい(298頁の連続と不連続の説明も重要)。微分・積分の説明(232頁)なども中高生に読んでもらいたい。*
フェルマーの原理:
↗︎
____/____
l___/_____lガラス板
/
光
↗︎
____/___
l___/____lガラス板
/
光
「光は、その通過時間が最小になるような経路を選んで通る」(82頁)
下の方が余計に通過時間がかかる(83頁より)
(直線を曲線にするにはつまみを1個から2個にする。119頁)
ll
\/
117頁より
パスが直線の場合 パスが曲線の場合
つまみ1個で全部の つまみは2個以上必要
パスを表示できる
(フェルマーの原理のように (ポントリャーギン理論では
入射角、反射角が等しいのが一般的) 最大のスイッチがあればいい)
ただし続編に振り分けられるDSGE(動学的確率的一般均衡モデル)については本書ではわからない。
DSGEについては、直接DSGEについての言葉ではないが、205頁より以下の言葉が的確だ。
《「ミクロ的基礎づけ」も…適度の範囲でのみ有効》140頁
《「ミクロ的基礎づけ」も…適度の範囲でのみ有効》140頁
これはラムゼーモデルが本来人口を変数に入れていないことからもわかる。評判は悪いがソローモデルがマルサスを受け継いでいることは軽視出来ない。
さらに、
「経済学を学ぶ目的は、それを使って経済政策のあれこれの問題を解くことではなく、経済学者に騙されないためだ」
というジョーン・ロビンソンの言葉が引用される(142頁)。経済動学を専門家だけのブラックボックスにしないためにも本書は重要だ。
さらに、
「経済学を学ぶ目的は、それを使って経済政策のあれこれの問題を解くことではなく、経済学者に騙されないためだ」
というジョーン・ロビンソンの言葉が引用される(142頁)。経済動学を専門家だけのブラックボックスにしないためにも本書は重要だ。
書評用
メモ:
89頁
初代=フェルマーの原理(82~3頁)
2代目=「解析力学」ラグランジュ(113,178,207頁),ニュートン(237頁)
3代目=「最適制御理論」(89,103,108頁) ,ポントリャーギン(300頁) \量子力学(138頁)
4代目=最新マクロ経済学の動的均衡理論
/
146頁 /
(1)ラムゼイ・モデル(131,152,156頁)
(2)RBCモデル(173頁)
(3)ニューIS-LMモデル(198頁)
(4)インフレ・ターゲット理論(151,205頁)DSGE
初代=フェルマーの原理(82~3頁)
2代目=「解析力学」ラグランジュ(113,178,207頁),ニュートン(237頁)
3代目=「最適制御理論」(89,103,108頁) ,ポントリャーギン(300頁) \量子力学(138頁)
4代目=最新マクロ経済学の動的均衡理論
/
146頁 /
(1)ラムゼイ・モデル(131,152,156頁)
(2)RBCモデル(173頁)
(3)ニューIS-LMモデル(198頁)
(4)インフレ・ターゲット理論(151,205頁)DSGE
I「オイラー方程式」(159,163頁)
II 「制約条件」(178,180頁)
III「ラグランジュ乗数」(207頁)
フェルマーの原理(82頁)*→経済学は物理学ではなく生物学(225頁)に出自があるし****
最速降下線の問題(113頁)→DSGE(205頁)**の何たるかはこれではわからないし
ポントリャーギン理論(300頁)→連続と不連続(298頁)より離散をもっとダイレクトに(300頁)語るべきだが…
(前著あとがきにあった三体問題(43頁)に冒頭で言及したのは正しい)
それでも長沼経済数学本は名著だ
「方程式***の意味など教えてもらうまでもない」
「こんなことはわかってる」
「これは間違いだ」
「他の本の方がいい」
そんなことは言わず買った方がいい
長沼氏の過去の経済関連の記事☆を読んで疑っていたが杞憂だった
☆
現代経済学の直感的方法 電子出版
http://pathfind.motion.ne.jp/economics.htm
*
フェルマーの原理:
↗︎
____/____
l___/_____lガラス板
/
光
↗︎
____/___
l___/____lガラス板
/
光
「光は、その通過時間が最小になるような経路を選んで通る」(82頁)
http://pathfind.motion.ne.jp/economics.htm
*
フェルマーの原理:
↗︎
____/____
l___/_____lガラス板
/
光
↗︎
____/___
l___/____lガラス板
/
光
「光は、その通過時間が最小になるような経路を選んで通る」(82頁)
下の方が余計に通過時間がかかる(83頁より)
通過時間→ラグランジュラン(ラグランジュ関数102頁)=L(100頁)へ
(直線を曲線にするにはつまみを1個から2個にする。119頁)
ll
\/
117頁より
パスが直線の場合 パスが曲線の場合
__C__ ((
/\ C点の位置が ( )パスA
左右に動く パスB
←〇→ ←〇→
つまみを左右に ←〇→
動かす
つまみ1個で全部の つまみは2個以上必要
パスを表示できる
117頁
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhouHWCCr96d50NvFndItN4eWrnl-Grb_o2c5KS3VMg4EoVyyMkELwnFFCX4v0KkPXyg0mWPYeM7O8Gr6W9_DLRRW74gIYkxMrvXuHLOzIFlfnOsgotN1HySLJz_0muoLlyIi8sRw/s640/blogger-image-1336949843.jpg
(直線を曲線にするにはつまみを1個から2個にする。119頁)
ll
\/
117頁より
パスが直線の場合 パスが曲線の場合
__C__ ((
/\ C点の位置が ( )パスA
左右に動く パスB
←〇→ ←〇→
つまみを左右に ←〇→
動かす
つまみ1個で全部の つまみは2個以上必要
パスを表示できる
117頁
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhouHWCCr96d50NvFndItN4eWrnl-Grb_o2c5KS3VMg4EoVyyMkELwnFFCX4v0KkPXyg0mWPYeM7O8Gr6W9_DLRRW74gIYkxMrvXuHLOzIFlfnOsgotN1HySLJz_0muoLlyIi8sRw/s640/blogger-image-1336949843.jpg
(フェルマーの原理のように (ポントリャーギン理論では
入射角、反射角が等しいのが一般的) 最大のスイッチがあればいい)
入射角、反射角が等しいのが一般的) 最大のスイッチがあればいい)
**
DSGEについては、205頁より以下の言葉が的確、
《「ミクロ的基礎づけ」も…適度の範囲でのみ有効》140頁
DSGEについては、205頁より以下の言葉が的確、
《「ミクロ的基礎づけ」も…適度の範囲でのみ有効》140頁
***
238頁より、図、
堂々巡りを逆手にとった方程式:
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjfCdAhFkDUNLe_KGasTH56eDj6dQR-Vm0Z_QRQms3Va371NoESlGlZUZybRoA5Uioc6NdH1y1aDKCyfr4R6Y81ETJVGgESFACUDQ1SGUQkx9yZV57bsx-t_Xug_TPn4DiqHTVkTQ/s640/blogger-image-1784239336.jpg
3.ラグランジュ乗数とハミルトニアンの関連性
効用最適化ラグランジュ、最小化を志向(218頁)
ハミルトニアンは全体が一定、λラムダ一定(最適)比率(217頁)
H=W+λf (213頁)
「このH(つまり全エネルギー)全体を常に一定に保っていく」ことがハミルトニアンの基本思想(212~3頁)
(226頁に「持続可能な経済」に向けたHの可能性)
271頁より、行列と固有値のイメージ:
交渉2回目 交渉1回目
o|o o|o
o | o o | o
| |
__o___|___o____ __o___|___o_
o | o |
o | o o | o
o| o o|o
|半径は拡大して交渉決裂ヘ |
交渉3回目
固有値が1の時には定常的な関係が成り立つ
固有値が1の時には定常的な関係が成り立つ
この半径(絶対値)が双方の
興奮度·強硬度を示す
交渉2回目 交渉1回目
交渉3回目
半径は拡大して交渉決裂ヘ
この半径(絶対値)が双方の興奮度·強硬度を示す
固有値が1の時には定常的な関係が成り立つ
_____
NAMs出版プロジェクト: 長沼伸一郎『経済数学の直観的方法 マクロ経済学編』:目次
http://nam-students.blogspot.jp/2016/09/blog-post_17.html
http://nam-students.blogspot.jp/2016/09/blog-post_17.html
経済数学の直観的方法 マクロ経済学編 (ブルーバックス)
2016/09/15
類書と志が違う。これを読んでからローマー(171頁)や加藤(198頁) を読むべきだ。
批判しかしない人間を批判する罠にハマるな
ボブ・ディラン
あなたのために簡単なメロディがかけたらなあ
淑女のあなたから、狂気と痛み、無駄な知識を遠ざけるようなメロディを
Tombstone Blues - Bob Dylan (ボブ ・ ディラン)
http://www.songaah.com/ja/lyrics/tombstone-blues.html
Now, I wish I could write you a melody so plain
歌詞の意味: 今、私は一目瞭然なので、メロディを書くことができる希望します。
That could hold you, dear lady, from going insane
歌詞の意味: 正気からの親愛なる女性、あなたを保持することができます。
That could ease you and cool you and cease the pain
歌詞の意味: 容易にすることができる冷却して痛みを停止
Of your useless and pointless knowledge
歌詞の意味: あなたの役に立たないと無意味な知識
ラムゼイモデルにこだわらない意味、ラムゼイモデルの特殊性(173,194頁)も参考になる。
オイラー方程式(161頁)が経済学と物理学では違う使われ方をするというのも面白い(165頁)。
制約条件(146,179頁)が大事になる。固有値(265,270頁)も本書で初めてイメージが掴めた。
第6章はミクロ経済学の基礎。
ジェーン・ロビンソン(142頁)の名言が中級編最後に引用される。
序文
http://bluebacks.kodansha.co.jp/intro/201/
http://bookclub.kodansha.co.jp/product?isbn=9784062579841
価格 定価 : 本体1,200円(税別)
ISBN 978-4-06-257984-1
判型 新書
ページ数 320ページ
著:長沼伸一郎(ナガヌマシンイチロウ)
理系学生伝説の参考書『物理数学の直観的方法』著者が、文系向けに難解な経済数学の要諦を斬新な切り口で分かりやすく解説する。
理系学生伝説の参考書『物理数学の直観的方法』の著者による、画期的な経済数学の入門書。
現代の経済学は、物理学に基づく高度な数学を取り入れているため、難解なイメージがあります。本書では、理系と文系の中央位置から、双方を視野に入れる独自のアプローチを取っているため、直観的な理解の道を拓くことができます。
経済数学の二大難解理論である「動学的マクロ均衡理論」「ブラック・ショールズ理論」。この2つの理論の頂上部分を直観的に理解することで、今まで難物だった他のこまごまとした数学技法を、ちょうど一番高い2つの山からそれより低い山を見下ろす要領で、精神的に呑んでかかって楽に理解できるようにします。
本書「マクロ経済学編」では、二大難解理論の一方で、経済学の最重要理論である「動学的マクロ均衡理論」を一気に理解することを可能にします。
本書では、専門課程の学生のための本格的な数学的部分を後半部分に集中させることで、前半部分は一般読者でも読めるように工夫されています。そのため経済学部の学生が本書を数学の難所突破の特効薬として使うのはもちろん、一般読者の方々も、本書を数少ないこれらの一般向けの解説書として使うこともできます。
______
http://bluebacks.kodansha.co.jp/intro/201/
http://bookclub.kodansha.co.jp/product?isbn=9784062579841
価格 定価 : 本体1,200円(税別)
ISBN 978-4-06-257984-1
判型 新書
ページ数 320ページ
著:長沼伸一郎(ナガヌマシンイチロウ)
理系学生伝説の参考書『物理数学の直観的方法』著者が、文系向けに難解な経済数学の要諦を斬新な切り口で分かりやすく解説する。
理系学生伝説の参考書『物理数学の直観的方法』の著者による、画期的な経済数学の入門書。
現代の経済学は、物理学に基づく高度な数学を取り入れているため、難解なイメージがあります。本書では、理系と文系の中央位置から、双方を視野に入れる独自のアプローチを取っているため、直観的な理解の道を拓くことができます。
経済数学の二大難解理論である「動学的マクロ均衡理論」「ブラック・ショールズ理論」。この2つの理論の頂上部分を直観的に理解することで、今まで難物だった他のこまごまとした数学技法を、ちょうど一番高い2つの山からそれより低い山を見下ろす要領で、精神的に呑んでかかって楽に理解できるようにします。
本書「マクロ経済学編」では、二大難解理論の一方で、経済学の最重要理論である「動学的マクロ均衡理論」を一気に理解することを可能にします。
本書では、専門課程の学生のための本格的な数学的部分を後半部分に集中させることで、前半部分は一般読者でも読めるように工夫されています。そのため経済学部の学生が本書を数学の難所突破の特効薬として使うのはもちろん、一般読者の方々も、本書を数少ないこれらの一般向けの解説書として使うこともできます。
______
本書を読んで思い出した、
批判しかしない人間を批判する罠にハマるな
ボブ・ディラン
あなたのために簡単なメロディがかけたらなあ
淑女のあなたから、狂気と痛み、無駄な知識を遠ざけるようなメロディを
Tombstone Blues - Bob Dylan (ボブ ・ ディラン)
http://www.songaah.com/ja/lyrics/tombstone-blues.html
Now, I wish I could write you a melody so plain
歌詞の意味: 今、私は一目瞭然なので、メロディを書くことができる希望します。
That could hold you, dear lady, from going insane
歌詞の意味: 正気からの親愛なる女性、あなたを保持することができます。
That could ease you and cool you and cease the pain
歌詞の意味: 容易にすることができる冷却して痛みを停止
Of your useless and pointless knowledge
歌詞の意味: あなたの役に立たないと無意味な知識
______
物理数学の直観的方法 <普及版> 追加原稿電子版 http://pathfind.motion.ne.jp/physics/
53×8×4-6+2-5=
1687
+×-÷
√ 立方根
物理数学の直観的方法 <普及版> 追加原稿電子版
http://pathfind.motion.ne.jp/physics/
「1687」
この数字は、ニュートンの「プリンキピア」が出版された年号
この数字は、ニュートンの「プリンキピア」が出版された年号
_____
最適制御論
評価指標を与え、それを最小化(又は最大化)することで、最適な制御系を与えることを目的とした理論。1960年代に最適出力フィードバックに関する研究がさかんに行われたが、最も代表的なのは2次形式の評価関数

を最小化にする状態フィードバック入力を求めるもので、最適レギュレータ (Optimal Regulator) と呼ばれる。その解はリッカチ代数方程式 (Riccati Algebraic Equation)

の正定対称解 を元に、
を元に、
 を元に、
を元に、
で与えられる。
____
スラスターは右方向に最大強度で噴射,左に倒すと左方向に最大強度で噴射という具合に,一定強度でしか噴射できない構造になっているものが多いのである。
操縦桿を右や左に倒して最短時間で目標にたどり着こうとする際には,操縦桿は左右いずれの方向であれ,とにかく「目一杯倒す」ことが必要だということである。
そのため操縦桿を倒せる最大角度を「α°」として右方向を+,左方向を-で表し,各時点で操縦桿を倒す角度の値を,時間tを横軸にとったグラフで表現すると,それは+αと-αの値だけをジャンプして行ったり来たりする不連続関数のグラフとなり,これは振り子を最短時間で止める問題でも同じようなことになる。そしてまた宇宙空間で姿勢制御用のスラスターを吹かしてそれを行う場合も同様で,追跡すべき目標物が振り子のように往復運動するパターンだった場合,それを最短時間で追跡するには,スラスターの最大噴射強度をFとしたとき,それは+Fと-Fの間を行ったり来たりする不連続関数となるのである。(次の図6.8)
(またはa°)
+F| ___ ___
+F| ___ ___
| : : :
| : : :
| : : :
__|____:___:___:___→t
| : : :
| : : :
-F|____: :___:
| : : :
| : : :
-F|____: :___:
(または-a°)
そして先ほどのポントリャーギン理論の興味深い結果は,数学的には「解が凸集合(凸多面体)の頂点になる」という言葉でも表現される。
____
「財政学は何を間違ってきたのか」|批判的頭脳
http://ameblo.jp/nakedcds/entry-12173998083.html
先ほど述べた「貯蓄はゼロであるべき」という条件は、時間割引率を用いて厳密に定義すると、「時間割引した貯蓄がゼロに収束するべき」という条件で定義される。この条件のことを横断性条件という。(NPG[No-Ponzi Game]条件と称されることもある)
この場合、実は貯蓄は増加しても横断性条件を満たせる場合がある。時間割引率以下の増加は、貯蓄の現在割引価値を増やさないからだ。逆に、時間割引率以上の貯蓄増加は起こり得ない。そういう場合は、時間割引率=金利が引きあがる場合か、貯蓄の実質的な価値が下がる…インフレによる貯蓄減価が生じる場合だけになる。
ということで、横断性条件は簡単に言えば時間割引率≧貯蓄増加率、すなわち金利≧貯蓄増加率で表現できることになる。
ここで、貯蓄とは、常に誰かに対する「貸し」である。預金だとしても、国債だとしても、株だとしても、それぞれ銀行、政府、企業への「貸し」になっている。というわけで、必ず「負債」が対になっている。預金は銀行の負債で、国債は政府の負債である。株は会計上企業の負債ではない(企業は返済義務がない)が、資金循環上は負債として扱われる。直接返済するのは企業ではなく、他の株式投資家ということになるだろう。 (参考 資金循環統計 )
よって、横断性条件は、貯蓄と同値のものとしての負債に対する条件だと見做すことが出来る。金利≧負債増加率が横断性条件となる。
当然のことながら、日本は全くこの条件を満たしていない。1990~2015年の政府債務の増加率は手計算で年複利でみて6%弱であった。金利はその期間のうちのほとんどを低空飛行している。
数学的には、前期債務増分×定率のプライマリーバランス改善でも横断性条件が満たされる(Bohn条件 )のだが、井堀・土居はそれも成立していないと分析している。
この分析で財政学者はどういう結論を得たのだろうか。
ここで財政学者は、「国債金利は異様に低すぎる」⇒「今は国債バブルであり、国債金利は横断性条件が示す水準に”収斂”しなければならない」と考えるのである。そして、ベースマネー供給により金利の収斂を回避した場合は、債務の実質価値の低下として、インフレがもたらされると予言するのである。(横断性条件を通じ、債務増加率から物価を推定する分析を、Fiscal Theory of Price Level FTPL 物価水準の財政理論というのだが、その成績は芳しくないという批判が絶えない 参考:「マネタリズムもFTPLもインフレ予測に役に立たない」
http://ameblo.jp/nakedcds/entry-12173998083.html
先ほど述べた「貯蓄はゼロであるべき」という条件は、時間割引率を用いて厳密に定義すると、「時間割引した貯蓄がゼロに収束するべき」という条件で定義される。この条件のことを横断性条件という。(NPG[No-Ponzi Game]条件と称されることもある)
この場合、実は貯蓄は増加しても横断性条件を満たせる場合がある。時間割引率以下の増加は、貯蓄の現在割引価値を増やさないからだ。逆に、時間割引率以上の貯蓄増加は起こり得ない。そういう場合は、時間割引率=金利が引きあがる場合か、貯蓄の実質的な価値が下がる…インフレによる貯蓄減価が生じる場合だけになる。
ということで、横断性条件は簡単に言えば時間割引率≧貯蓄増加率、すなわち金利≧貯蓄増加率で表現できることになる。
ここで、貯蓄とは、常に誰かに対する「貸し」である。預金だとしても、国債だとしても、株だとしても、それぞれ銀行、政府、企業への「貸し」になっている。というわけで、必ず「負債」が対になっている。預金は銀行の負債で、国債は政府の負債である。株は会計上企業の負債ではない(企業は返済義務がない)が、資金循環上は負債として扱われる。直接返済するのは企業ではなく、他の株式投資家ということになるだろう。 (参考 資金循環統計 )
よって、横断性条件は、貯蓄と同値のものとしての負債に対する条件だと見做すことが出来る。金利≧負債増加率が横断性条件となる。
当然のことながら、日本は全くこの条件を満たしていない。1990~2015年の政府債務の増加率は手計算で年複利でみて6%弱であった。金利はその期間のうちのほとんどを低空飛行している。
数学的には、前期債務増分×定率のプライマリーバランス改善でも横断性条件が満たされる(Bohn条件 )のだが、井堀・土居はそれも成立していないと分析している。
この分析で財政学者はどういう結論を得たのだろうか。
ここで財政学者は、「国債金利は異様に低すぎる」⇒「今は国債バブルであり、国債金利は横断性条件が示す水準に”収斂”しなければならない」と考えるのである。そして、ベースマネー供給により金利の収斂を回避した場合は、債務の実質価値の低下として、インフレがもたらされると予言するのである。(横断性条件を通じ、債務増加率から物価を推定する分析を、Fiscal Theory of Price Level FTPL 物価水準の財政理論というのだが、その成績は芳しくないという批判が絶えない 参考:「マネタリズムもFTPLもインフレ予測に役に立たない」
_____
M B K 48 : ラムゼイモデルで人口減少を見る
http://blog.livedoor.jp/sowerberry/archives/39590192.html
http://blog.livedoor.jp/sowerberry/archives/39590192.html
以前に同じような記事を書きましたが、説明が正確でなかったので訂正版を書きました。
結論から言うと、ラムゼイモデルでは人口減少の「現実的な」影響を説明することができないように思います。
以下、知識(技術)の増加率を g、人口成長率を n、時間割引率(時間選好率)を ρ とします。また、消費の効用関数の限界効用の弾力性(にマイナスを掛けたもの)をθとします(異時点間の代替性は、1/θ となります)。資本消耗はないと想定します。
(1)ローマ、『上級マクロ経済学』のモデル
資本の動学は、
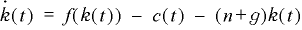
(1)
消費の動学は、
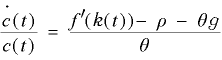
(2)
で表されます( k・(t) = dk(t)/dt です) 。
定常状態では、dc/dt 、dk/dt が 0 になります( dc/dt =0、dk/dt =0)。
まず、dk/dt =0 の軌跡を求めると、(1)式の左辺が 0 になるということなので、定常状態での効率労働当たりの資本ストックを k とすると、
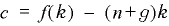
(3)
が成り立ちます。消費 c は、生産関数 f(k) と直線 (n+g)k との差になる、ということです。
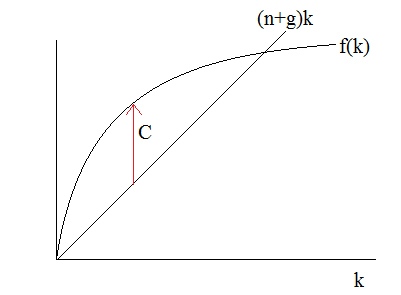
図1
したがって、dk/dt =0 の軌跡をを (k,c) の空間に描けば(c は、 f(k) から (n+g)k を引いたものです) 、図2のような上に凸の曲線になります。
次に、dc/dt =0 の軌跡を求めると、(2)式の左辺が 0 になるということなので、
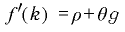
(4)
が成り立ちます。したがって、dc/dt =0 の軌跡は、(4)式を満たす k になります。これは、図2のような縦の直線になります((4)式に c がないので)。
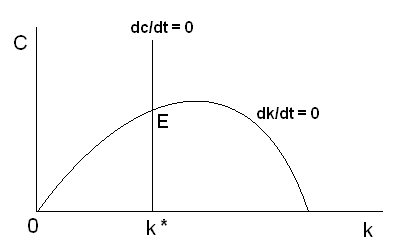
図2
結論から言うと、ラムゼイモデルでは人口減少の「現実的な」影響を説明することができないように思います。
以下、知識(技術)の増加率を g、人口成長率を n、時間割引率(時間選好率)を ρ とします。また、消費の効用関数の限界効用の弾力性(にマイナスを掛けたもの)をθとします(異時点間の代替性は、1/θ となります)。資本消耗はないと想定します。
(1)ローマ、『上級マクロ経済学』のモデル
資本の動学は、
(1)
消費の動学は、
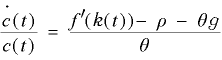
(2)
で表されます( k・(t) = dk(t)/dt です) 。
定常状態では、dc/dt 、dk/dt が 0 になります( dc/dt =0、dk/dt =0)。
まず、dk/dt =0 の軌跡を求めると、(1)式の左辺が 0 になるということなので、定常状態での効率労働当たりの資本ストックを k とすると、
(3)
が成り立ちます。消費 c は、生産関数 f(k) と直線 (n+g)k との差になる、ということです。

図1
したがって、dk/dt =0 の軌跡をを (k,c) の空間に描けば(c は、 f(k) から (n+g)k を引いたものです) 、図2のような上に凸の曲線になります。
次に、dc/dt =0 の軌跡を求めると、(2)式の左辺が 0 になるということなので、
(4)
が成り立ちます。したがって、dc/dt =0 の軌跡は、(4)式を満たす k になります。これは、図2のような縦の直線になります((4)式に c がないので)。

図2
定常状態は、dk/dt =0 と dc/dt =0 との交点です。図2の E です。
ここで人口増加率 n が低下したとします。 (2)式、あるいは(4)式には n がないので、dc/dt =0 の直線はシフトしません。
いっぽう、(1)式、あるいは(3)式には n が入っています。したがって、dk/dt=0 の軌跡は変化します。(3)式から、n が小さくなると、c が大きくなる、とわかります。dk/dt=0 の軌跡は上へシフトします(下の図3)。
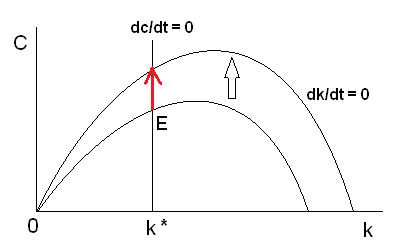
図3
定常状態は、dk/dt =0 と dc/dt =0 との交点です。経済は図3のEから、新たな定常状態へ向かって上へ移動します。ラムゼイモデルでは、消費 c はジャンプ変数(操作変数)です。瞬時に変化できます(いっぽう、資本 k は状態変数で、すぐに変化できない。資本ストック k は「その経済において歴史的に決定されており・・・不連続に変化することはできない」。対照的に、消費 c は、「変化(ショック)の生じたその時点において不連続に変化(ジャンプ)できる(ローマー、78ページ) 注1)。
したがって、この場合( kの変化は生じないので)、新たな均衡への移動は、瞬時に(比較的短い時間で)行われます。
効率労働当たりの資本 k は変化せず、効率労働当たりの消費が増加することになります。ただし、経済全体のGDP(産出量)は減少します。経済成長率は次の式で表されます。
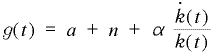
a は知識・技術の増加率。a も資本ストック(第3項)も変化していなくて、n(人口増加率)が減少するので、経済成長率は減少します。
こういうこと(1人当たりの消費が増加する)が、人口が減少している今の日本で起こっている(あるいは起こった)と考えるのは難しい。
(2)ブランシャール("Lectures on Macroeconomics") のモデル 資本の動学は、ローマーと同じ、
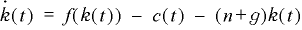
です。消費の動学は、ローマーとはちがうものです。
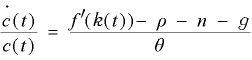
(5)
(この式の導出はこちらを参照してください。注2)。
人口増加率nが減少した場合、dk/dt =0 の軌跡の変化は、ローマーの場合と同じです。上へシフトします(下の図4)。
dc/dt =0 の軌跡の変化は、ローマーの場合と違います。それを求めると、(5)式の左辺 dc/dt が 0 になる、ということなので、
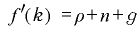
(6)
が成り立ちます。これは図2と同じ縦の直線です。
しかし、(6)式の場合、n が減少すると、f’(k) が減少します。f’(k) が減少すれば、k は増加します。したがって、n が減少すると、dk/dt =0 の軌跡は右にシフトします(下の図4)。
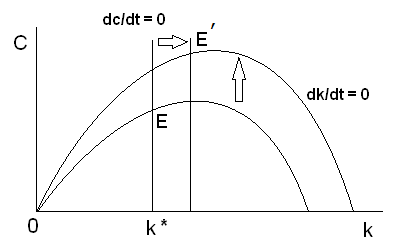
図4
経済は、新たな均衡 E’に移動するのですが、これだけではどのような動きをするのかわかりません。均衡に到達する経路は、鞍点経路(サドルパス)です。サドルパスが E よりも上にあるか、下にあるかで経済の動きが違うものになるからです。
(a) サドルパスが E よりも上にある場合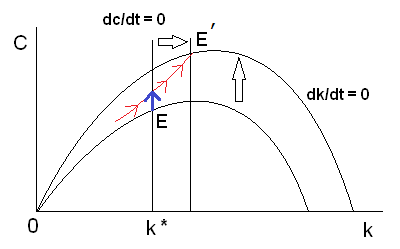
図5
経済は、まず、サドルパスまで上へジャンプします。消費 c はジャンプ変数で、瞬時に変化できます。その後、サドルパスに従って、新たな均衡 E’へ長い時間をかけて進んでいくことになります。
このパターンの場合、最初、効率労働当たりの消費が瞬時的に増え、その後、効率労働当たりの資本と消費がじわじわと増加していくことになります。
(b) サドルパスが E よりも下にある場合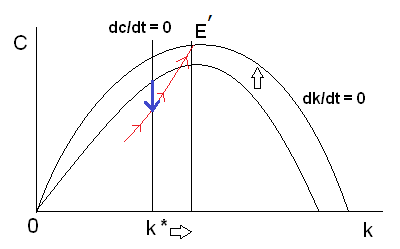
図6
経済は、まずサドルパスまで下へジャンプします。その後、サドルパスに従って、資本と消費を増やしながら、新たな均衡へゆっくりと進んでいきます。
このパターンの場合、最初、効率労働当たりの消費が瞬時的に減少し、その後、効率労働当たりの資本と消費がじわじわと増加していくことになります。
いったん消費を減少させるのは、将来、1人当たりの資本ストックが増加すること――正確に言えば、将来の1人当たりの資本ストックを増加させれば効用最大化できること――がわかっています(ラムゼイモデルは合理的期待モデルです)。資本を増加させるために、いったん消費を減らすのです。
さて、上の3つのパターンのどれが、現在の日本の人口減少の状況に近いでしょうか。
3つめのパターンが今の日本の状況に近いように思えます(消費が一時的に減るから)。しかし、消費がいったん減少するのは、将来、1人当たりの資本ストックが増加すると人々が期待している(そして、消費も増加する)からです。これが今の日本の状況に当てはまるとは思えません。
なぜ、図6で新たな均衡 E’が右上にあるのに、経済は右上に動かずに、下に移動するのか?
E から右上に動いていくと、下の図7のように、(位相図の動学にしたがい)紫の矢印のにしたがって F の方向に進み、消費が増大し、資本を食いつぶすことになります。わざわざ厚生を悪化させる方向に進むのは非合理的です。
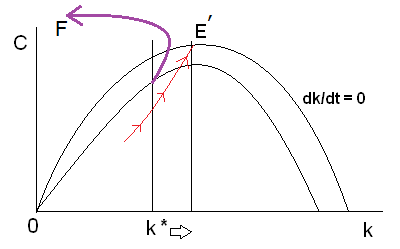
図7
消費(ジャンプ変数、操作変数)は調整可能です。経済は縦方向には自由に動けます。新たな均衡 E’に到達する経路はサドルパス(だけ)です。経済は新たな均衡E’に到達できるように、消費を不連続に変化させ(消費を減少させ)、サドルパスに乗るようにするのです。
注1) 斎藤他『マクロ経済学』のラムゼイモデルの説明に物足りなさを感じるのはこの点です。
消費 c は、ジャンプ変数(操作変数)で不連続に変化できる。いっぽう資本 k は、状態変数で連続的にしか変化できない(この説明は、チャンの『現代経済学の数学』にもあります)。
この区別が書かれていません。
そのため、上の図7のような、Fに至る経路が起こりうるかのような印象を与える説明になっています。
注2) なぜ、ローマーのモデルでは、消費の動学方程式に人口増加率 n が入ってこず、ブランシャールのモデルでは人口増加率 n が入ってくるのかわかりません。想定している予算制約式が違います。ブランシャールの場合、資本の動学方程式を予算制約式にしています。
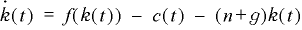
逆に、ローマーの予算制約式の仮定をどのように変えれば、人口増加率 n が入ってくるようになるのかわかりません。たぶん、効用最大化の単位が家計当たり[家計の効用を最大化する]か、1人当たり[1人の個人の効用を最大化する。こちらには人口増加率の n が入ってくる]か、という違いだと思うのですが・・・ どうでしょうか?
ここで人口増加率 n が低下したとします。 (2)式、あるいは(4)式には n がないので、dc/dt =0 の直線はシフトしません。
いっぽう、(1)式、あるいは(3)式には n が入っています。したがって、dk/dt=0 の軌跡は変化します。(3)式から、n が小さくなると、c が大きくなる、とわかります。dk/dt=0 の軌跡は上へシフトします(下の図3)。

図3
定常状態は、dk/dt =0 と dc/dt =0 との交点です。経済は図3のEから、新たな定常状態へ向かって上へ移動します。ラムゼイモデルでは、消費 c はジャンプ変数(操作変数)です。瞬時に変化できます(いっぽう、資本 k は状態変数で、すぐに変化できない。資本ストック k は「その経済において歴史的に決定されており・・・不連続に変化することはできない」。対照的に、消費 c は、「変化(ショック)の生じたその時点において不連続に変化(ジャンプ)できる(ローマー、78ページ) 注1)。
したがって、この場合( kの変化は生じないので)、新たな均衡への移動は、瞬時に(比較的短い時間で)行われます。
効率労働当たりの資本 k は変化せず、効率労働当たりの消費が増加することになります。ただし、経済全体のGDP(産出量)は減少します。経済成長率は次の式で表されます。
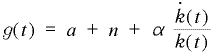
a は知識・技術の増加率。a も資本ストック(第3項)も変化していなくて、n(人口増加率)が減少するので、経済成長率は減少します。
こういうこと(1人当たりの消費が増加する)が、人口が減少している今の日本で起こっている(あるいは起こった)と考えるのは難しい。
(2)ブランシャール("Lectures on Macroeconomics") のモデル 資本の動学は、ローマーと同じ、
です。消費の動学は、ローマーとはちがうものです。
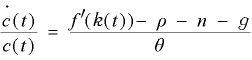
(5)
(この式の導出はこちらを参照してください。注2)。
人口増加率nが減少した場合、dk/dt =0 の軌跡の変化は、ローマーの場合と同じです。上へシフトします(下の図4)。
dc/dt =0 の軌跡の変化は、ローマーの場合と違います。それを求めると、(5)式の左辺 dc/dt が 0 になる、ということなので、
(6)
が成り立ちます。これは図2と同じ縦の直線です。
しかし、(6)式の場合、n が減少すると、f’(k) が減少します。f’(k) が減少すれば、k は増加します。したがって、n が減少すると、dk/dt =0 の軌跡は右にシフトします(下の図4)。

図4
経済は、新たな均衡 E’に移動するのですが、これだけではどのような動きをするのかわかりません。均衡に到達する経路は、鞍点経路(サドルパス)です。サドルパスが E よりも上にあるか、下にあるかで経済の動きが違うものになるからです。
(a) サドルパスが E よりも上にある場合

図5
経済は、まず、サドルパスまで上へジャンプします。消費 c はジャンプ変数で、瞬時に変化できます。その後、サドルパスに従って、新たな均衡 E’へ長い時間をかけて進んでいくことになります。
このパターンの場合、最初、効率労働当たりの消費が瞬時的に増え、その後、効率労働当たりの資本と消費がじわじわと増加していくことになります。
(b) サドルパスが E よりも下にある場合

図6
経済は、まずサドルパスまで下へジャンプします。その後、サドルパスに従って、資本と消費を増やしながら、新たな均衡へゆっくりと進んでいきます。
このパターンの場合、最初、効率労働当たりの消費が瞬時的に減少し、その後、効率労働当たりの資本と消費がじわじわと増加していくことになります。
いったん消費を減少させるのは、将来、1人当たりの資本ストックが増加すること――正確に言えば、将来の1人当たりの資本ストックを増加させれば効用最大化できること――がわかっています(ラムゼイモデルは合理的期待モデルです)。資本を増加させるために、いったん消費を減らすのです。
さて、上の3つのパターンのどれが、現在の日本の人口減少の状況に近いでしょうか。
3つめのパターンが今の日本の状況に近いように思えます(消費が一時的に減るから)。しかし、消費がいったん減少するのは、将来、1人当たりの資本ストックが増加すると人々が期待している(そして、消費も増加する)からです。これが今の日本の状況に当てはまるとは思えません。
なぜ、図6で新たな均衡 E’が右上にあるのに、経済は右上に動かずに、下に移動するのか?
E から右上に動いていくと、下の図7のように、(位相図の動学にしたがい)紫の矢印のにしたがって F の方向に進み、消費が増大し、資本を食いつぶすことになります。わざわざ厚生を悪化させる方向に進むのは非合理的です。

図7
消費(ジャンプ変数、操作変数)は調整可能です。経済は縦方向には自由に動けます。新たな均衡 E’に到達する経路はサドルパス(だけ)です。経済は新たな均衡E’に到達できるように、消費を不連続に変化させ(消費を減少させ)、サドルパスに乗るようにするのです。
注1) 斎藤他『マクロ経済学』のラムゼイモデルの説明に物足りなさを感じるのはこの点です。
消費 c は、ジャンプ変数(操作変数)で不連続に変化できる。いっぽう資本 k は、状態変数で連続的にしか変化できない(この説明は、チャンの『現代経済学の数学』にもあります)。
この区別が書かれていません。
そのため、上の図7のような、Fに至る経路が起こりうるかのような印象を与える説明になっています。
注2) なぜ、ローマーのモデルでは、消費の動学方程式に人口増加率 n が入ってこず、ブランシャールのモデルでは人口増加率 n が入ってくるのかわかりません。想定している予算制約式が違います。ブランシャールの場合、資本の動学方程式を予算制約式にしています。
逆に、ローマーの予算制約式の仮定をどのように変えれば、人口増加率 n が入ってくるようになるのかわかりません。たぶん、効用最大化の単位が家計当たり[家計の効用を最大化する]か、1人当たり[1人の個人の効用を最大化する。こちらには人口増加率の n が入ってくる]か、という違いだと思うのですが・・・ どうでしょうか?
______
最速降下曲線 - Wikipedia
https://ja.wikipedia.org/wiki/%E6%9C%80%E9%80%9F%E9%99%8D%E4%B8%8B%E6%9B%B2%E7%B7%9A
https://ja.wikipedia.org/wiki/%E6%9C%80%E9%80%9F%E9%99%8D%E4%B8%8B%E6%9B%B2%E7%B7%9A
最速降下曲線(さいそくこうかきょくせん 英: Brachistochrone curve)は、任意の2点間を結ぶ全ての曲線のうちで、曲線上に軌道を束縛された物体に対して重力 (に代表される保存力) のみが作用する仮定の下、物体が速度0でポテンシャルが高い方の点を出発してからもう一方の点に達するまでの所要時間がもっとも短いような曲線である。
最速降下曲線はサイクロイドである。AとBが与えられAがBよりも高いとき、Aを無限斜面で通り、またBも通りAとBの間で最大値をとらない上下逆のサイクロイドがひとつだけある。これが最速降下曲線である。したがって最速降下曲線は物体の重さと重力定数の強さにはよらない。この問題は変分法の道具を使って解くことが出来る。 注意すべきは、Aで初速度があったり、摩擦が考慮されていると時間を最小にする曲線は上記の曲線から外れることである。
サイクロイドであることの証明
フェルマーの原理より、2点間で光のビームが通る実際の道筋は、最短の時間で光が横切るものである。したがって最速降下曲線は、光が媒質の中で垂直方向の加速を受けるとき(gを重力加速度とする )の光のビーム軌道である。エネルギー保存則を用いれば、h を現在の位置とはじめの位置との高さの差とすると、物体が一定の重力の中にあるときその速度は

となる。速度は水平方向の変位によらないことに注意。 θは軌道が垂直方向となす角とする。スネルの法則によれば軌道上で光のビームは次の式に従う:
 .
. は最高速度である。(
は最高速度である。(  が最大値1となるとき)
が最大値1となるとき)
上記の式の速度を代入すると次の2つの結論が得られる。
- 粒子の速度がゼロの始めは角度はゼロである。したがって最速降下曲線は原点で垂直方向である。(つまり下方向)
- 速度は軌道が水平になるとき最大である。
簡単のために粒子(またはビーム)が座標(0, 0)から離れているとして、最大速度が高さD で得られると考える。
 .
.
すべての軌道上の位置で軌道の傾き角度θは(x,y)座標では次のように表される:
 .
.
この式を前の式に代入し項を整理しなおすと次の式が結果として得られる:
 .
.
ここで半径rのサイクロイドの微分方程式は
 .
.
である。比較すると、結果の式は半径 の円が作る反対のサイクロイドの微分方程式である。
の円が作る反対のサイクロイドの微分方程式である。
 の円が作る反対のサイクロイドの微分方程式である。
の円が作る反対のサイクロイドの微分方程式である。歴史
ガリレオは1638年に著書"Two New Sciences"で、最速降下曲線は円弧であるとしたが誤りであった。ヨハン・ベルヌーイは(以前に解析した当時曲線を参照して)この問題を解いた後、1696年6月に著書"Acta Eruditorum"で読者に対して問題を提示した。4人の数学者がこれに応じて解答した。アイザック・ニュートン、ヤコブ・ベルヌーイ(ヨハンの兄)、ゴットフリート・ライプニッツ、ギヨーム・ド・ロピタルである。ロピタルを除く3人の解答は1697年の同じ版で出版された。
弟に対抗してヤコブ・ベルヌーイはより難しい最速降下曲線問題を作った。それを解いている間に新しい手法を開発し、それがレオンハルト・オイラーによって改良され後に変分法と呼ばれるものになった。ジョゼフ=ルイ・ラグランジュは現代の微積分学に帰着するさらなる仕事を進めた。
ニュートンとライプニッツの間の異なった競争もまたこの発展に貢献している。最速降下曲線問題を相手より先に解いたとそれぞれが主張している。また計算法における次の仕事でも彼らは言い争いを続けている。
語源
ギリシャ語で"brachistos"は最も短いという意味で、"chronos"は時間という意味である。
関連項目
外部リンク
- Weisstein, Eric W., "Brachistochrone Problem" - MathWorld.(英語)
- Iagsoft's "Brachistochrone Construction" (Java applet)
- www.mathcurve.com (フランス語だが、わかりやすい動画が見られるサイト)
Pour - de - de - de - de | 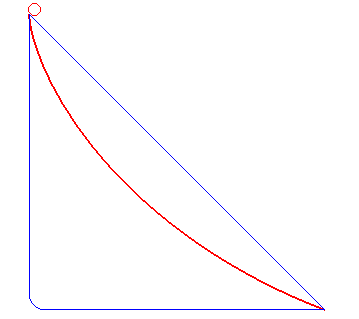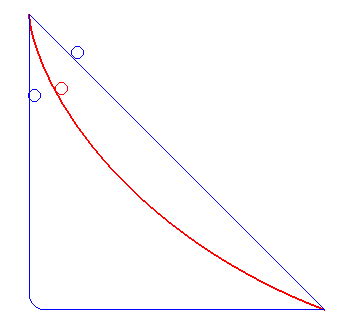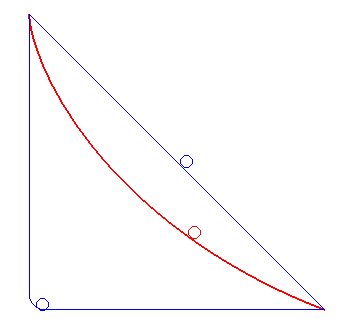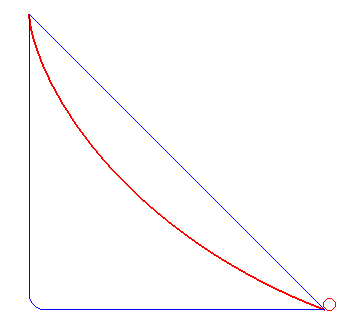 |








16 Comments:
9/17
投稿者 30代女性
レビュー対象商品: 経済数学の直観的方法 マクロ経済学編 (ブルーバックス) (新書)
物理数学の直観的方法の著者長沼伸一郎さんの書籍の経済学バージョン。
こんなマニアックな本と思ったけど、何気にアマゾンの経済学分野で一位に輝いてるwww
一応、私も政治経済学部の経済学よりの授業を多くとってきたので、経済数学にはヒイヒイ言わされたので
こういう本が学生時代にあれば良かったなと思った。
マクロ経済学を図解で分かりやすく学ぶなら「マンキューマクロ経済学」もお薦めだけれど、そこを一歩踏み込
んで、数学的な知見を織り込みつつも数学が得意でない人間が数学的な経済モデリングまで踏み込むなら、
こっちでフォローアップするのもいいね。
経済数学は、多変数関数の解析が多く出てくるんだけど、そのなかの変数のどれを止めて、どれを動かすかで
パラメータが変わった時のインパクトを知るというものになりますが、その原理について丁寧に解説された書籍です。
基本的に中学一年生でならった式の展開ができて、微分ができれば、この書籍の4分の3までは読み進める
ことができるような気がする。うん。たぶん。
残りは行列の計算ですが、「あー、そうだった~」と苦手意識を思い出しながら、読むのもオツなもの。
星五つでもいいくらいですが、図やイラストがもう少し欲しかったという欲もあり四つ星で。
89頁
初代=フェルマーの原理
2代目=「解析力学」ラグランジュ
3代目=「最適制御理論」
4代目=最新マクロ経済学の動的均衡理論
/
146頁 /
(1)ラムゼイ・モデル
(2)RBCモデル
(3)ニューIS-LMモデル
(4)インフレ・ターゲット理論
長沼本のような本は専門馬鹿には書けないしその意義が理解出来ない
9月6日は黒澤明の命日
Akira Kurosawa (1910-1998)
「くだらん奴が、くだらんという事は、くだらんものではない証拠で、つまらん奴がつま
らんという事は、大変面白いという事でしょう」
(直線を曲線にするにはつまみを1個から2個にする。119頁)
ll
\/
117頁より
パスが直線の場合 パスが曲線の場合
つまみ1個で全部の つまみは2個以上必要
パスを表示できる
(フェルマーの原理のように (ポントリャーギン理論では
入射角、反射角が等しいのが一般的) 最大のスイッチがあればいい)
本書は物理数学の立場から経済動学へと至る段階を人類史的に四段ロケットのように分け、さらに経済動学自体を四段に分けている。前半(入門・中級編)の人類史的な部分が重要で、だからこそ上級編でもハミルトニアン(H)の基本思想である「このH(つまり全エネルギー)全体を常に一定に保っていく」(212~3頁)ことが「持続可能な経済」への可能性(226頁)を開くというような大胆な提言が出来るのだろう。
フェルマーの原理*を最初の動学の基本に据えた部分がオリジナルな発想だ。固有値やポントリャーギン理論の説明もわかりやすい。微分・積分の説明(232頁)なども中高生に読んでもらいたい。
*
フェルマーの原理:
↗︎
____/____
l___/_____lガラス板
/
光
↗︎
____/___
l___/____lガラス板
/
光
「光は、その通過時間が最小になるような経路を選んで通る」(82頁)
下の方が余計に通過時間がかかる(83頁より)
(直線を曲線にするにはつまみを1個から2個にする。119頁)
ll
\/
117頁より
パスが直線の場合 パスが曲線の場合
つまみ1個で全部の つまみは2個以上必要
パスを表示できる
(フェルマーの原理のように (ポントリャーギン理論では
入射角、反射角が等しいのが一般的) 最大のスイッチがあればいい)
ただし続編に振り分けられるDSGMについては本書ではわからない。
DSGMについては、直接DSGMについての言葉ではないが、205頁より以下の言葉が的確だ。
《「ミクロ的基礎づけ」も…適度の範囲でのみ有効》140頁
さらに、
「経済学を学ぶ目的は、それを使って経済政策のあれこれの問題を解くことではなく、経済学者に騙されないためだ」
というジョーン・ロビンソンの言葉が引用される(142頁)。経済動学を専門家だけのブラックボックスにしないためにも本書は重要だ。
NAMs出版プロジェクト: 長沼伸一郎『経済数学の直観的方法 マクロ経済学編』:目次
http://nam-students.blogspot.jp/2016/09/blog-post_17.html
長沼伸一郎「経済数学の直観的方法 マクロ経済学編」
https://itun.es/jp/xLw7eb.l
経済数学の直観的方法 マクロ経済学編 (ブルーバックス) 電子書籍: 長沼伸一郎: Kindleストア
https://www.amazon.co.jp/dp/B01M1RFG08
(ブルーバックス)2016/09/15
本書は物理数学の立場から経済動学へと至る段階を人類史的に四段ロケットのように分け、さらに
経済動学自体を四段に分けている。前半(入門・中級編)の人類史的な部分が重要で、だからこそ上級
編でもハミルトニアン(H)の基本思想である「このH(つまり全エネルギー)全体を常に一定に保って
いく」(212~3頁)ことが「持続可能な経済」への可能性(226頁)を開くというような大胆な提言が出来るのだろう。
I「オイラー方程式」(159,163頁)
II 「制約条件」(178,180頁)
III「ラグランジュ乗数」(207頁)
この3つの原理が全編の鍵になる。
フェルマーの原理*を最初の動学の基本に据えた部分がオリジナルな発想だ。固有値やポントリャーギン
理論の説明もわかりやすい。微分・積分の説明(232頁)なども中高生に読んでもらいたい。
*
フェルマーの原理:
↗︎
____/____
l___/_____lガラス板
/
光
↗︎
____/___
l___/____lガラス板
/
光
「光は、その通過時間が最小になるような経路を選んで通る」(82頁)
下の方が余計に通過時間がかかる(83頁より)
(直線を曲線にするにはつまみを1個から2個にする。119頁)
ll
\/
117頁より
パスが直線の場合 パスが曲線の場合
つまみ1個で全部の つまみは2個以上必要
パスを表示できる
(フェルマーの原理のように (ポントリャーギン理論では
入射角、反射角が等しいのが一般的) 最大のスイッチがあればいい)
ただし続編に振り分けられるDSGMについては本書ではわからない。
DSGMについては、直接DSGMについての言葉ではないが、205頁より以下の言葉が的確だ。
《「ミクロ的基礎づけ」も…適度の範囲でのみ有効》140頁
さらに、
「経済学を学ぶ目的は、それを使って経済政策のあれこれの問題を解くことではなく、経済学者
に騙されないためだ」
というジョーン・ロビンソンの言葉が引用される(142頁)。経済動学を専門家だけのブラックボックス
にしないためにも本書は重要だ。
か長沼伸一郎「経済数学の直観的方法 マクロ経済学編」
https://itun.es/jp/xLw7eb.l
経済数学の直観的方法 マクロ経済学編 (ブルーバックス) 電子書籍: 長沼伸一郎: Kindleストア
https://www.amazon.co.jp/dp/B01M1RFG08
(ブルーバックス)2016/09/15
本書は物理数学の立場から経済動学へと至る段階を人類史的に四段ロケットのように分け、さらに
経済動学自体を四段に分けている。前半(入門・中級編)の人類史的な部分が重要で、だからこそ上級
編でもハミルトニアン(H)の基本思想である「このH(つまり全エネルギー)全体を常に一定に保って
いく」(212~3頁)ことが「持続可能な経済」への可能性(226頁)を開くというような大胆な提言が出来るのだろう。
I「オイラー方程式」(159,163頁)
II 「制約条件」(178,180頁)
III「ラグランジュ乗数」(207頁)
この3つの原理が全編の鍵になる。
フェルマーの原理*を最初の動学の基本に据えた部分がオリジナルな発想だ。固有値やポントリャーギン
理論の説明もわかりやすい。微分・積分の説明(232頁)なども中高生に読んでもらいたい。
ただし続編に振り分けられるDSGMについては本書ではわからない。
DSGMについては、直接DSGMについての言葉ではないが、205頁より以下の言葉が的確だ。
《「ミクロ的基礎づけ」も…適度の範囲でのみ有効》140頁
さらに、
「経済学を学ぶ目的は、それを使って経済政策のあれこれの問題を解くことではなく、経済学者
に騙されないためだ」
というジョーン・ロビンソンの言葉が引用される(142頁)。経済動学を専門家だけのブラックボックス
にしないためにも本書は重要だ。
*
フェルマーの原理:
↗︎
____/____
l___/_____lガラス板
/
光
↗︎
____/___
l___/____lガラス板
/
光
「光は、その通過時間が最小になるような経路を選んで通る」(82頁)。下の方が余計に通過時間がかかる。
長沼伸一郎「経済数学の直観的方法 マクロ経済学編」(ブルーバックス)2016/09/23(15)
https://itun.es/jp/xLw7eb.l ibooks
https://www.amazon.co.jp/dp/B01M1RFG08 kindle
本書は物理数学の立場から経済動学へと至る段階を人類史的に四段ロケットのように分け、さらに
経済動学自体を四段に分けている。前半(入門・中級編)の人類史的な部分が重要で、だからこそ上級
編でもハミルトニアン(H)の基本思想である「このH(つまり全エネルギー)全体を常に一定に保って
いく」(212~3頁)ことが「持続可能な経済」への可能性(226頁)を開くというような大胆な提言が出来るのだろう。
I「オイラー方程式」(159,163頁) II 「制約条件」(178,180頁) III「ラグランジュ乗数」(207頁)
この3つの原理が全編の鍵になる(146頁)。
フェルマーの原理*を最初の動学の基本に据えた部分がオリジナルな発想だ。固有値やポントリャーギン
理論の説明もわかりやすい。微分・積分の説明(232頁)なども中高生に読んでもらいたい。
ただし続編に振り分けられるDSGMについては本書ではわからない。
DSGMについては、直接DSGMについての言葉ではないが、205頁より以下の言葉が的確だ。
《「ミクロ的基礎づけ」も…適度の範囲でのみ有効》140頁
さらに、
「経済学を学ぶ目的は、それを使って経済政策のあれこれの問題を解くことではなく、経済学者
に騙されないためだ」
というジョーン・ロビンソンの言葉が引用される(142頁)。経済動学を専門家だけのブラックボックス
にしないためにも本書は重要だ。
*
フェルマーの原理:
↗︎
____/____
l___/_____lガラス板
/
光
↗︎
____/___
l___/____lガラス板
/
光
「光は、その通過時間が最小になるような経路を選んで通る」(82頁)。下の方が余計に通過時間がかかる。
長沼伸一郎「経済数学の直観的方法 マクロ経済学編」(ブルーバックス)2016/09/23(15)
https://itun.es/jp/xLw7eb.l ibooks
https://www.amazon.co.jp/dp/B01M1RFG08 kindle
本書は物理数学の立場から経済動学へと至る段階を人類史的に四段ロケットのように分け、さらに
経済動学自体を四段に分けている。前半(入門・中級編)の人類史的な部分が重要で、だからこそ上級
編でもハミルトニアン(H)の基本思想である「このH(つまり全エネルギー)全体を常に一定に保って
いく」(212~3頁)ことが「持続可能な経済」への可能性(226頁)を開くというような大胆な提言が出来るのだろう。
I「オイラー方程式」(159,163頁) II 「制約条件」(178,180頁) III「ラグランジュ乗数」(207頁)
この3つの原理が全編の鍵になる(146頁)。
フェルマーの原理*を最初の動学の基本に据えた部分がオリジナルな発想だ。固有値やポントリャーギン
理論の説明もわかりやすい(298頁の連続と不連続の説明も重要)。微分・積分の説明(232頁)なども中高生に読んでもらいたい。
ただし続編に振り分けられるDSGMについては本書ではわからない。
DSGMについては、直接DSGMについての言葉ではないが、205頁より以下の言葉が的確だ。
《「ミクロ的基礎づけ」も…適度の範囲でのみ有効》140頁
さらに、
「経済学を学ぶ目的は、それを使って経済政策のあれこれの問題を解くことではなく、経済学者
に騙されないためだ」
というジョーン・ロビンソンの言葉が引用される(142頁)。経済動学を専門家だけのブラックボックス
にしないためにも本書は重要だ。
*
フェルマーの原理:
↗︎
____/____
l___/_____lガラス板
/
光
↗︎
____/___
l___/____lガラス板
/
光
「光は、その通過時間が最小になるような経路を選んで通る」(82頁)。下の方が余計に通過時間がかかる。
類書と志が違う。これを読んでからローマー(171頁)や加藤(198頁) を読むべきだ。
ラムゼイモデルにこだわらない意味、ラムゼイモデルの特殊性(173,194頁)も参考になる。
オイラー方程式(161頁)が経済学と物理学では違う使われ方をするというのも面白い(165頁)。
制約条件(146,179頁)が大事になる。固有値(265,270頁)も本書で初めてイメージが掴めた。
第6章はミクロ経済学の基礎。
長沼伸一郎「経済数学の直観的方法 マクロ経済学編」(ブルーバックス)2016/09/23(15)
https://itun.es/jp/xLw7eb.l ibooks
https://www.amazon.co.jp/dp/B01M1RFG08 kindle
類書と志が違う。これを読んでからローマー(171頁)や加藤(198頁) を読むべきだ。
ラムゼイモデルにこだわらない意味、ラムゼイモデルの特殊性(173,194頁)も参考になる。
オイラー方程式(161頁)が経済学と物理学では違う使われ方をするというのも面白い(165頁)。
制約条件(146,179頁)が大事になる。固有値(265,270頁)も本書で初めてイメージが掴めた。
第6章はミクロ経済学の基礎。
本書は物理数学の立場から経済動学へと至る段階を人類史的に四段ロケットのように分け、さらに
経済動学自体を四段に分けている。前半(入門・中級編)の人類史的な部分が重要で、だからこそ上級
編でもハミルトニアン(H)の基本思想である「このH(つまり全エネルギー)全体を常に一定に保って
いく」(212~3頁)ことが「持続可能な経済」への可能性(226頁)を開くというような大胆な提言が出来るのだろう。
I「オイラー方程式」(159,163頁) II 「制約条件」(178,180頁) III「ラグランジュ乗数」(207頁)
この3つの原理が全編の鍵になる(146頁)。
フェルマーの原理*を最初の動学の基本に据えた部分がオリジナルな発想だ。固有値やポントリャーギン
理論の説明もわかりやすい(298頁の連続と不連続の説明も重要)。微分・積分の説明(232頁)なども中高生に読んでもらいたい。
ただし続編に振り分けられるDSGMについては本書ではわからない。
DSGMについては、直接DSGMについての言葉ではないが、205頁より以下の言葉が的確だ。
《「ミクロ的基礎づけ」も…適度の範囲でのみ有効》140頁
さらに、
「経済学を学ぶ目的は、それを使って経済政策のあれこれの問題を解くことではなく、経済学者
に騙されないためだ」
というジョーン・ロビンソンの言葉が引用される(142頁)。経済動学を専門家だけのブラックボックス
にしないためにも本書は重要だ。
*
フェルマーの原理:
↗︎
____/____
l___/_____lガラス板
/
光
↗︎
____/___
l___/____lガラス板
/
光
「光は、その通過時間が最小になるような経路を選んで通る」(82頁)。下の方が余計に通過時間がかかる。
動的計画法(どうてきけいかくほう、英: Dynamic Programming, DP)は、計算機科学の分野において、アルゴリズムの分類の1つである。 対象となる問題を複数の部分問題に分割し、部分問題の計算結果を記録しながら解いていく手法を総称してこう呼ぶ。
あなたの人生の物語 Kindle版
テッド チャン (著), 浅倉久志 (翻訳)
5つ星のうち 3.9 69件のカスタマーレビュー
映画メッセージ原作短編
フェルマーの原理が出てくる
長沼伸一郎 「現代経済学の直観的方法」
私たちが生きる現代資本主義社会の本質とその問題、行く末を直観的に理解する一冊!
(目次)
第1章 資本主義はなぜ止まれないのか
第2章 農業経済はなぜ敗退するのか
第3章 インフレとデフレのメカニズム
第4章 貿易はなぜ拡大するのか
第5章 ケインズ経済学とは何だったのか
第6章 貨幣はなぜ増殖するのか
第7章 ドルはなぜ国際経済に君臨したのか
第8章 仮想通貨とブロックチェーン
第9章 資本主義経済の将来はどこへ向かうのか
kndle
20200408
【無料お試し版】現代経済学の直観的方法 Kindle版
長沼伸一郎 (著)
その他()の形式およびエディションを表示する
Kindle版 (電子書籍)
¥0
今すぐお読みいただけます: 無料アプリ
【無料お試し版】わかりやすくて、おもしろくて、深い。
かつて『物理数学の直観的方法』で理系世界に一大センセーションを巻き起こした著者による、
この一冊で資本主義の本質をガツっと直観的につかむ、
どこにもなかった経済書。
・資本主義とは
・インフレとデフレのメカニズム
・貿易が拡大する理由とは?
・ケインズ経済学とは何か?
・貨幣の本質とは?
・なぜドルは強いのか?
・仮想通貨(暗号資産)とブロックチェーンとは何か?
そして、
・資本主義社会の最大の問題点と、その解決のヒント
私たちが生きる現代資本主義社会の本質とその問題、行く末を理解する一冊!
(目次)
第1章 資本主義はなぜ止まれないのか
第2章 農業経済はなぜ敗退するのか
第3章 インフレとデフレのメカニズム
第4章 貿易はなぜ拡大するのか
第5章 ケインズ経済学とは何だったのか
第6章 貨幣はなぜ増殖するのか
第7章 ドルはなぜ国際経済に君臨したのか
第8章 仮想通貨とブロックチェーン
第9章 資本主義経済の将来はどこへ向かうのか
#3のみ読める
そしてここで再び第 1章を振り返ると 、そこでは 「政府が金利を上げ下げすることが 、鉄道の輸送効率のコントロ ールにつながっている 」という話があった 。そもそも先ほどの話のように 、刷ったばかりの紙幣をどんどん流し込むなどというのは 、あくまでも非常事態のもとでの最後の手段に過ぎない 。通常のまともな経済状態のもとでは 、そんな乱暴なことは行わないのであり 、そのコントロ ールはもっぱら金利を上げ下げすることによって行われるのが普通である 。要するにこの場合には 、金利を上げることでその鉄道にブレ ーキをかけ 、たとえ企業活動が補給不足で低調になるという不利をしのんでも 、民衆のインフレの災厄を抑え込むというわけであり 、これが新聞でよく目にする 、いわゆる 「金融引き締め策 」である 。あるいは読者の中には 、いままでその 「金融引き締め 」という言葉が頭の中でうまく絵になっていなかった 、という方もあるかもしれない 。しかしそういう読者でも 、このようにそれを第 1章の内容とうまく組み合わせて発展させることで 、より立体的にイメ ージを把握することができるのではないかと思う 。
〈要約 〉
・インフレという現象は 、基本的には物資と貨幣の対応バランスが崩れることで起こるものであり 、そのメカニズムをスマ ートに直観化するには 、本章図 3 ‐ 2のような逆ピラミッド型図形をイメ ージするのが最も早い 。
・ただ 、それは必ずしも造幣局が紙幣乱発をしたことで起こるものばかりではなく 、むしろその多くはサ ーキットが広くなっていく過程で生じたボトルネックが全体に波及していくというのに似たメカニズムによる 。そのため一般に好景気の状態はインフレを発生させやすい 。
・そして社会全体を眺めると 、インフレ状態のもとでは一般に社会にサンドイッチ状の損得が生じ 、資産家階層と労働者階層は損をする一方 、企業家階層は得をする傾向がある 。そのためインフレの良し悪しは 、視点をどの立場に置いて眺めるかで異なってくる 。
・景気を良くするためには 、政策当局はむしろ故意にある程度のインフレを期待することがあり 、それは昨今において多くの場所でしばしば見られている 。ただしその際には大勢の民衆の生活が犠牲になっており 、もしそちらへの対応を優先してインフレを防止しようと思った場合には 、経済社会の鉄道にブレ ーキをかけて資金の流入を絞ればよい 。そのためには金利を上げるのが有効なコントロ ール策で 、これがいわゆる 「金融引き締め策 」である 。
以上 、インフレとデフレについて最も基本的なことを述べてきたが 、これらの話は後の第 5章などでも重要になるので 、特に三つの階層で利害が異なるという話などは 、頭の隅に留めておくとよいだろう 。
●つづきは製品版でお読みください 。
コメントを投稿
<< Home