わかった気になる？一般均衡理論―ブラウワーの不動点定理の証明付き―
http://kansai.me/kiishimizu/pdf/kinko.pdf
1 は じ め に
交換経済（財の生産を行わず，各消費者が持っている財の交換だけで成り立つ経済）における均衡，正確には均衡価格の存在を考える．財が3つ以上ある経済における均衡の存在を証明するにはブラウワーの不動点定理を用いる．
X0, X1, …, Xnのn＋1(n≧1)財からなる交換経済がありそれぞれの価格をpi(≧0), i＝0, 1, …, nとする．p0＋p1＋…+pn＝として
i＝pi，i＝0, 1, …, nと
定義し0,1, …,nをあらためてp0, p1, …, pnと書くと
p0＋p1＋…＋pn＝1 （1）
が成り立つ．交換経済における消費者の需要（超過需要，自分の初期保有量を超える需要）は相対価格によって決まるのでこのようにして価格の表現を変えても需要は変らない．ある消費者の各財の需要をxiとすると予算制約式は
p0x0＋p1x1＋…＋pnxn＝0
と表される（需要は超過需要であるから和がゼロになる）．両辺を＝p0＋p1…＋pnで割ると
0x0＋1x1＋…＋nxn＝0
となるから上記のように価格の表現を変えても予算制約式は変らない．したがって効用を最大化する需要も変らない．企業による生産を含む経済においても生産要素の価格も含めればやはり相対価格によって需要が決まる．このような性質は0次同次性と呼ばれる．n－1個までは財の価格がゼロでもよいが少なくとも2つの財の価格は正でなければならない．もしすべての価格あるいは1つの財以外の価格がゼロならばそれ以外（価格がゼロではない財以外）のどれかの財（あるいはすべての財）の需要が非常に大きくなりすぐに価格が正になると考えればよい．3財の場合には財をX, Y, Z, 価格をpx, py, pzと表すことにしよう．そのとき（1）はpx, py, pzを座標軸とする3次元空間において(1, 0, 0), (0, 1, 0), (0, 0, 1)を頂点とする三角形の辺と内部からなる図形を表している．三角形自体は2次元の図形である（第1図参照）．この三角形（∆とする）に含まれる点を同じ三角形（これを∆´とする）の点に対応させる写像（関数）を考える．∆のある点は∆´の異なる（異なる位置にある）点に対応するかもしれないし，同じ点に対応するかもしれない．後者の場合その点は不動点であると言う．∆の1つの点は∆´の1つの点に対応する．しかし∆の異なる点が∆´の同じ点に対応するかもしれない．また，この対応は連続であると仮定する．すなわち∆上のごく近くの点同士は∆´のごく近くの点に対応する．
スペルナーの定理
| スペルナーの定理 台集合のサイズがmである単体的複体 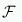 において、サイズがiの要素の個数をFiとすると、Fi-1 ≧ (i／(m－i＋1))・Fi が成り立つ。 |
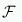に含まれる集合の部分集合はすべて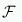に含まれることから、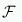- に含まれるサイズiの要素1つに対して、その部分集合としてi個、サイズi－1の要素が存在 している。
(i個の要素から1つ取り除く方法はi通りあるため。)
- 逆に、サイズi－1の要素の方から見ると、その要素を含むサイズiの要素の個数は高々m－i＋1個である。
(i－1個の要素に1つ付け加える方法はm－i＋1通りあるため。)
ここで、包含関係のあるようなサイズiの集合とサイズi－1の集合の組の個数をxとすると、
- 1つ目の観察から x＝i・Fi、
- 2つ目の観察から x≦(m－i＋1)Fi-1
i・Fi≦(m－i＋1)Fi-1
すなわち、Fi-1 ≧ (i／(m－i＋i))・Fiという不等式が得られることになる。
(証明終り)
注： このように、ある性質を満たす集合族(この場合は単体的複体である、つまり、部分集合に閉じている集合族)に対して、限界ぎりぎりの状況ではどのようなことが起こっているか？(この場合は、Fi-1をどこまで下げられるか？)というような議論は、「極値集合論」(extremal set theory)と呼ばれる分野で行なわれている。離散数学・組合せ論の重要な分野の一つである。
経済分析第120号 応用一般均衡モデルと公共政策｜内閣府 経済社会総合研究所
http://www.esri.go.jp/jp/archive/bun/bun120/bun120.html
財政学をはじめ専門諸分野で提起される経済政策効果に関する純理論的分析と実証的な応用分析の水準の間には、上記のいくつかの税制改革シミュレーション例が示すように、相当のギャップが現在もなお依然として解消されずに残っている。このような非整合的とも言うべき経済分析上の格差を埋める新しい手法が、応用一般均衡 (Applied General Equilibrium, 略称AGE) モデルを利用するアプローチである。
AGE分析手法の開発は、1960年代半ば頃米国エール大学の数理経済学者H.スカーフ(Scarf)によってなされた均衡価格(数学的には不動点)を近似値に算出するアルゴリズム (algorithm, 解法手順) の考案が、もっとも大きなきっかけになっている。従来のワルラス型モデルにおける一般均衡は、位相数学の「不動点定理」を使ってその存在のみが示唆されるにとどまっていたが、スカーフ・アルゴリズムは均衡解の存在証明の別証明 (いわゆる constructive proof) を提示し、同時に均衡解そのものを有限回の反復計算により実際に解くことを可能にしたのである。1)
『環境政策と一般均衡』で解説しているプログラムの紹介とダウンロード
http://eco.genv.sophia.ac.jp/epam/pubprog/pubprog.html| で用いられている プログラムの紹介とダウンロード | |
| 上記著作では、実用的応用一般均衡モデルＥＰＡＭの解説のほかに、応用一般均衡モデルの二部門モデルの構築例とプログラムの解説を行っている。ＥＰＡＭについては、この「わしだネット」の中で、プログラムの全体を紹介している。ここでは、上記著作の中の二部門モデルおよびスカーフとメリルの不動点アルゴリズムのプログラムを紹介しダウンロードできるようにした。 プログラムの使い方については、上記著作に詳しく解説しています。 なお、すべてのプログラムの著作権は、鷲田豊明に属しています。 ダウンロードし解凍すると次のような６個のプログラムが現れます。 | |
| プログラム名 | 機能 |
| excessd.c | ３財２人の純粋交換均衡における超過需要計算プログラム。価格を与えると、そのもとでの超過需要を出力する。 |
| scarf.c | スカーフのアルゴリズムのＣプログラム。仮説の均衡解を設定し、そのもとでの超過需要をexcessd.cに問い合わせ、収束判定をする。 |
| merrill.c | メリルのアルゴリズムのＣプログラム。仮説の均衡解を設定し、そのもとでの超過需要をexcessd.cに問い合わせ、収束判定をする。 |
| main.c | メリルのアルゴリズム用のメインプログラム。 |
| 2sectexd.c | 二部門応用一般均衡モデルの超過需要計算プログラム。 |
| 2sect.c | 二部門応用一般均衡モデルのメインプログラム。 |
| プログラムのダウンロード | |
| 次の三つのファイルは中身はどれも同じです。自分のシステムにあったものをダウンロードしてください。 | |
| pubepam.exe | Windows用の自己解凍型ファイルです。適当なフォルダにダウンロードして、ダブルクリックすれば、ファイルが解凍できます。 |
| pubepam.lzh | Windows, Mac, Linux のいずれでもＯＫ。Lhaが必要です。 |
| pubepam.tar.gz | Windows, Mac, Linux のいずれでもＯＫ。tarが必要です。 |
https://www.minervashobo.co.jp/book/b96153.html
著者 室山 義正 シリーズ監修
浦井 憲 著
吉町 昭彦 著
ジャンル テキスト > 経済 > ミクロ経済学
経済
シリーズ 経済 > Minerva ベイシック・エコノミクス
出版年月日 2012年04月15日
ISBN 9784623062683
判型・ページ数 A5・364ページ
ミクロ経済学 - ミネルヴァ書房 ―人文・法経・教育・心理・福祉などを刊行する出版社
https://www.minervashobo.co.jp/book/b96153.html
緒 言
序 章 経済学理論について
市場と自由
個人と社会
合理性と経済学
第１章 基礎的概念
1.1 経 済
1.1.1 経済と人間 1.1.2 経済の語源
1.2 交 換
1.2.1 交換と交易
1.3 商 品
1.3.1 共通の様式を持つもの 1.3.2 商品空間
1.4 価 格
1.4.1 価格空間 1.4.2 価値の理論ということ
1.5 消費と生産
1.5.1 行為としての消費と生産 1.5.2 価値と行為
1.6 日付と出来事
1.6.1 日付と出来事（Date-Event） および市場
1.7 貨幣と市場
1.7.1 歴史的な貨幣 1.7.2 流通貨幣（通貨）と銀行
1.7.3 貨幣と今日的な市場構造
1.8 市場と均衡
1.8.1 市場と予想そして均衡と合理性
1.8.2 予想と貨幣（世代重複モデルと貨幣的均衡）
1.9 我々の世界観は果たしてどこまで広くなったのか
1.10 現実社会の諸相
1.10.1 グローバルな金融市場 1.10.2 飢餓と貧困・自由貿易
1.10.3 原発事故を巡って
第２章 個人の選択と社会の状態
2.1 選 好
2.1.1 合理的選好 2.1.2 効用関数表現
2.1.3 補論─辞書式選好 2.1.4 顕示選好の弱公理
2.1.5 補論─選択対応
2.2 社会選択
2.2.1 アローの不可能性定理
2.3 均衡と合理性
2.3.1 非協力ゲーム 2.3.2 合理性の共通認識
2.3.3 ナッシュ均衡 2.3.4 純粋戦略と混合戦略
2.3.5 ナッシュ均衡と非協力ゲームの解 2.3.6 期待効用
第３章 消費および生産の理論
3.1 消費の理論
3.1.1 効用最大化問題の解
3.1.2 好ましさの向きを代表するベクトル 3.1.3 顕示選好理論
3.1.4 双対分析 3.1.5 価格効果・代替効果・所得効果
3.2 生産の理論
3.2.1 利潤最大化問題の解 3.2.2 技術と時間および不確実性
3.2.3 双対分析 3.2.4 部分均衡論のための費用関数と供給関数
3.3 補論─制約条件付最大値問題
第４章 均衡分析とその応用
4.1 部分均衡と余剰分析
4.1.1 準線形の効用関数 4.1.2 需要曲線と供給曲線
4.1.3 余剰分析
4.2 一般均衡と厚生
4.2.1 エッジワース・ボックス・ダイアグラム
4.2.2 ワルラス法則と模索過程
4.3 投入産出分析
4.3.1 GDP等価 4.3.2 国民経済とLP双対問題
4.3.3 斉一成長経路とフォンノイマン成長モデル
4.4 ケインズ均衡
4.4.1 IS-LM 分析
4.5 国際経済と交換のはたらき・その他
4.5.1 弾力性 4.5.2 くもの巣理論
4.5.3 比較生産費説─リカードの定理
4.5.4 へクシャー=オリーンの定理 4.5.5 要素価格均等化命題
4.5.6 国際貿易その他の定理
第５章 経済学的均衡の存在・一意性・安定性及び動学
5.1 不動点定理と静学的一般均衡
5.1.1 非協力ゲームとナッシュ均衡 5.1.2 抽象経済
5.1.3 一般均衡と厚生経済学の基本定理
5.2 超過需要関数からのアプローチ
5.2.1 顕示選好関係 5.2.2 粗代替性
5.2.3 超過需要関数とベクトル場 5.2.4 正則経済
5.2.5 スペルナーの補題とスカーフのアルゴリズム
5.2.6 ベクトル場のインデックス
5.3 一般均衡の動学的問題に向けて
第６章 不完全競争・市場の失敗・非対称情報
6.1 独占・寡占
6.1.1 寡占市場におけるゲーム論的均衡
6.1.2 寡占市場を含む一般均衡 6.1.3 法と経済
6.1.4 自然独占と限界費用価格付け
6.2 公共財と市場の失敗
6.2.1 外部性
6.3 情報の非対称性
6.3.1 非対称情報
6.3.2 非対称情報と市場の一般理論—市場の生き残り問題
6.4 不完備情報と不完全情報
6.4.1 展開形ゲーム 6.4.2 ナッシュ均衡の精緻化（Refinement）
6.4.3 繰り返しゲーム（Repeated Game）
6.5 今日的な経済学理論の構成形式
6.5.1 公理的特徴付け 6.5.2 社会選択関数
6.5.3 メカニズム・デザイン
終 章 経済学という世界観
経済学の方法論
経済学という世界観
経済学と倫理（社会と社会外）
索 引
スカーフのアルゴリズム(Scarf,1982) ：
３
／＼
３／＿＿＼２
／＼ ／＼
１／＿＿＼３＿＿＼３
／＼ ／＼ ／＼
３／＿＿＼３＿＿＼２＿＿＼２
／＼ ／＼ ☆↖︎↙︎ ↖︎＼
３／＿＿＼１＿＿＼１＿＿＼１＿↑_＼２
／＼ ／↗︎ ↘︎＼ ／↗︎ ／＼
１／＿＿＼１＿↑ _＼／＿↓_＼／＿↑_＼２＿＿＼２
／＼ ／＼
１／＿＿＼３＿＿＼３
／＼ ／＼ ／＼
３／＿＿＼３＿＿＼２＿＿＼２
／＼ ／＼ ☆↖︎↙︎ ↖︎＼
３／＿＿＼１＿＿＼１＿＿＼１＿↑_＼２
／＼ ／↗︎ ↘︎＼ ／↗︎ ／＼
１／＿＿＼１＿↑ _＼／＿↓_＼／＿↑_＼２＿＿＼２
￣－＿￣↗︎＿２＼ →１＿－￣＿－￣
↑ －＿￣－＼／－￣＿－￣
Ｓ:スタート地点
☆:停止点
１２３と揃ったフルラベルのついた小単体の部屋(均衡点を意味する)へと自動的に運ばれていくことになる(浦井憲ミクロ経済2012,247~8頁)。
参考：
ドブリュー『価値の理論』(1959,邦訳1977)は、数学的定義の後、生産→消費→均衡、
と記述が進む。一般的なミクロ経済学教科書の先駆だ。
その有効性に関してレオンチェフが疑問視したことも理解出来るが、一旦わかり始めると、スピノザを読むような爽快感がある。
(ただし同じ欲望を起点にしていても、ワルラスの定義はスピノザと比べると人間を矮小化している。コナトゥスの認識が足りないのである)。
以下の指摘が特に重要だと思う。
《私有制経済に関する均衡の存在証明の可否は、まさにγi の連続性にかかっているのである。》4.8 (107頁)
i(消費主体)
γi (可能な消費の非空集合(105頁)）
私有制経済 E=((Xi,前順序＜ i),(Yj),(ωi),(θij))
消費集合((Xi,前順序＜ i),
生産集合(Yj),
資源(ωi),
配当率(θij)) 5.7(171頁)
（前順序は擬順序と訳されている。記載方が分からなかったので漢字表記にした。）
以下、目次：
THEORY OF VALUE An Axiomatic Analysis of Economic Equilibrium by Gerard Debreu 1959
ジェラール・ドブリュー著
価値の理論
～経済均衡の公理的分析～
邦訳 丸山徹 1977,1988
目 次
日本語版への序文, 原著者序文
第1章 数学
1.1.序 - 1.2.集合 - 1.3.函数と対応 - 1.4.擬順序 - 1.5.実数 - 1.6.R^mにおける極限 - 1.7.連続函数 - 1.8.連続対応 - 1.9.R^mにおけるベクトル - 1.10.不動点 - 【ノート】
第2章 商品と価格
2.1.序論 - 2.2.日付と場所 - 2.3.財 - 2.4.用役 - 2.5.商品 - 2.6.価格 - 2.7.利子，割引，および交换 - 2.8.理論と解釈 - 【ノート】
第3章 生産者
3.1.序論 - 3.2.生産と生産集合 - 3.3.生産集合に関する仮定 - 3.4.利潤の最大化 - 3.5.価格の変化 - 【ノート】
第4章 消費者
4.1.序論 - 4.2.消費と消費集合 - 4.3.消費集合に関する仮定 - 4.4.選好 - 4.5.選好の非飽和性の仮定 - 4.6.選好の連続性の仮定 - 4.7.選好の凸性の仮定 - 4.8.富の制約 - 4.9.選好の充足 - 4.10.価格～富の変化 - 【ノート】
第5章 均衡
5.1.序論 - 5.2.資源 - 5.3.経済 - 5.4.達成可能状態 - 5.5.私有制経済 - 5.6.市場均衡 - 5.7.均衡 - 【ノート】
第6章 最適
6.1.序論 - 6.2.最適と価格体系に関しての均衡 - 6.3.価格体系に関しての均衡は最適である -
6.4.最適な状態はある価格体系に関して均衡である - 【ノート】
第7章 不確実性
7.1.序論 - 7.2.事象 - 7.3.商品と価格 - 7.4.生産者 - 7.5.消費者 - 7.6.均衡 - 7.7.最適
参考文献
［付録］数理経済均衡理論の四問題
1.経済均衡の存在 - 2.経済均衡の計算 - 3.正則微分可能な経済 - 4.大きな経済のコア
付録参考文献, 訳者あとがき, 記号表,
人名索引, 事項索引
経済分析第120号 応用一般均衡モデルと公共政策 - 経済社会総合研究所
AGE分析手法の開発は、1960年代半ば頃米国エール大学の数理経済学者H.スカーフ (Scarf)によってなされた均衡価格(数学的には不動点)を近似値に算出する アルゴリズム (algorithm, 解法手順) の考案が、もっとも大きなきっかけになっている。 従来の ...
状態(の変化)* on Twitter: "スカーフのアルゴリズムは不動点定理の単体 ...
スカーフのアルゴリズムは不動点定理の単体分割を有限回(exp(N)個)で打ち切った ことに相当するはず. View translation. Translated from Japanese by Bing Wrong translation? 6:33 PM - 11 Aug 2011. 0 retweets 0 favorites. Reply. Retweet.
