オイラーの公式・定理まとめ | 高校数学の美しい物語

オイラーの公式・定理まとめ | 高校数学の美しい物語
http://mathtrain.jp/euler_matome

オイラーの公式・定理まとめ

14/03/29

分野: まとめ

---

レオンハルト・オイラーは偉大な数学者で，いろいろな分野で業績を残しています。オイラーの定理，公式はたくさんあり，この他にもオイラーと名のつくものが存在しますが，主要なもの，高校数学で理解できるものを中心にまとめました。（順番は適当です）

美しい定理が並んでいますが，大学受験ではどれもほとんど使わないと思います。（4，6あたりは知っていると役に立つかもしれません）
数学オリンピックを目指す場合は7以外は知っておきたいところです。

1：チャップル・オイラーの定理

OI2=R2−2Rr$O{I}^2{R}^{2}2Rr$

外心と内心の距離を外接円の半径と内接円の半径のみで表した非常に美しい定理です。チャップルもオイラーとは独立に発見していたようです。
→オイラーの定理（初等幾何）

2：博士の愛した数式

eπi+1=0$e^{\pi i}10$

自然対数の底 e$e$，虚数単位 i$i$，円周率 π$\pi$ が共存する非常に美しい等式です。
→複素指数関数とオイラーの公式

3：オイラーの多面体定理

任意の穴の開いていない多面体において，
（頂点の数）-（辺の数）+（面の数）=2

全ての多面体に共通する非常に美しい性質です。
→オイラーの多面体定理の証明

4：オイラーの定理（整数論）

n$n$ を自然数，a$a$ を n$n$ と互いに素な整数としたとき，aϕ(n)≡1modn$a^{\varphi n}1\mathrm{m}\mathrm{o}\mathrm{d}n$

ϕ(n)$\varphi n$ は n$n$ と互いに素な 1$1$ から n−1$n1$ までの自然数の中で n$n$ と互いに素なものの個数を表し，オイラーの ϕ$\varphi$ 関数と呼ばれます。
→オイラーのファイ関数のイメージ

5：オイラーグラフ（一筆書き）

オイラーグラフ⇔全ての頂点から辺が偶数本出ている
準オイラーグラフ⇔辺が奇数本出ている頂点が2つのみ

一筆書きできるかできないか判定する方法です。
→オイラーグラフの定理とその証明

6：オイラー線

三角形の外心 O$O$，重心 G$G$，垂心 H$H$ は1直線上にあり，OG:GH=1:2$OGGH12$

この直線をオイラー線といいます。チャップル・オイラーの定理に勝るとも劣らない美しい定理です。
→オイラー線の3通りの証明

7：オイラー・ラグランジュ方程式（変分法）

これだけは高校範囲ではありませんが、、

∂L∂x−ddt∂L∂x˙=0${\displaystyle \frac{\mathrm{\partial }L}{\mathrm{\partial }x}}{\displaystyle \frac{d}{dt}}{\displaystyle \frac{\mathrm{\partial }L}{\mathrm{\partial }\stackrel{}{x}}}0$

ニュートンの運動方程式を変形していくとオイラー・ラグランジュ方程式になります。この方程式は変分法と呼ばれる手法の基礎になっており，大学で学びます。詳細は説明できませんが，変分法を学べば最速降下線や懸垂線の理解が深まります。

変分法の応用例：→懸垂線の2通りの導出☆

8：オイラーの公式（無限積）

オイラーの公式：
∏n=1∞cos(x2n)=cosx2cosx4cosx8⋯=sinxx${\displaystyle \underset{n1}{\overset{\mathrm{\infty }}{}}\cos {\displaystyle \frac{x}{2^n}}\cos {\displaystyle \frac{x}{2}}\cos {\displaystyle \frac{x}{4}}\cos {\displaystyle \frac{x}{8}}{\displaystyle \frac{\sin x}{x}}}$

→ヴィエトの無限積の公式

☆

懸垂線の２通りの導出 | 高校数学の美しい物語
http://mathtrain.jp/catenary

懸垂線の２通りの導出

14/03/21

分野: 指数・対数関数 　レベル: ★マニアック

---

紐の両端を手で持ってたらした曲線の式は
y=a(exa+e−xa)2$y{\displaystyle \frac{a{e}^{\frac{x}{a}}{e}^{\frac{x}{a}}}{2}}$

この曲線は懸垂線またはカテナリーと呼ばれる非常に有名な曲線です。懸垂線に関する入試問題はたまに出題されるので，知っておくべき性質をまとめた後に導出を紹介します。

懸垂線の有名な性質

・懸垂線は紐の両端を持ってたらした式
これは性質というより定義ですが，絶対に覚えておきましょう。鎖とか橋とかetc。ちなみに僕は懸垂線を見かけたら嬉しくなります（＾ω＾）

・放物線で近似できる
マクローリン展開を用いて原点付近で以下のように2次近似を行うことができます。
exa≃1+xa+x22a2,e−xa≃1−xa+x22a2$e^{\frac{x}{a}}1{\displaystyle \frac{x}{a}}{\displaystyle \frac{x^2}{2a^2}}{e}^{\frac{x}{a}}1{\displaystyle \frac{x}{a}}{\displaystyle \frac{x^2}{2a^2}}$ より，懸垂線は y=x22a+a$y{\displaystyle \frac{x^2}{2a}}a$ と近似できます。

・双曲線関数である
双曲線関数と呼ばれる有名な関数 sinhx,coshx$\sinh x\cosh x$ が存在します：
sinhx=ex−e−x2,coshx=ex+e−x2$\sinh x{\displaystyle \frac{e^x{e}^x}{2}}\cosh x{\displaystyle \frac{e^x{e}^x}{2}}$

双曲線関数は三角関数のように様々な関係式が成立し応用範囲も広く非常に重要な関数なのですが，高校ではあまり取りあげられていません。カテナリーは双曲線関数 acoshxa$a\cosh {\displaystyle \frac{x}{a}}$ と同じということを覚えておくとよいでしょう。

微分方程式を用いた導出

微分方程式は高校範囲外ですが，数3まで知っていれば以下の導出はなんとなく理解できると思われます。

1.微分方程式の導出

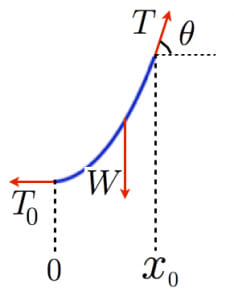
長い紐の一部 0≤x≤x0$0x{x}_0$ の区間を考える。両端にかかる張力を T0,T$T_{0}T$，紐にかかる重力を W$W$，x0$x_0$ での紐の角度を θ$\theta$ とおくと，T0$T_0$ は x0$x_0$ によらない定数なので（注），力の釣り合いから以下の式が成立する：
Tcosθ=T0,Tsinθ=W$T\cos \theta T_{0}T\sin \theta W$
よって，tanθ=WT0$\tan \theta {\displaystyle \frac{W}{T_0}}$
ここで，W$W$ は線の長さ s$s$ に比例するので，
dydx=tanθ=sa${\displaystyle \frac{dy}{dx}}\tan \theta {\displaystyle \frac{s}{a}}$（a$a$ は定数）と書ける。

注：もし x0$x_0$ を x0+Δx$x_0\mathrm{\Delta }x$ にしたときに T0$T_0$ が T′0$T_0^{}$に変化してしまうと，紐の x0$x_0$ から x0+Δx$x_0\mathrm{\Delta }x$ の部分に関して水平方向の釣り合いが成り立ちません。なぜなら，その部分では左側に T0$T_0$ の力が，右側には T′0$T_0^{}$の力がかかるからです。よって，T0$T_0$ は x0$x_0$によらず定数です。

2.微分方程式の解法

ds2=dx2+dy2$d{s}^{2}d{x}^{2}d{y}^2$ より，
dsdx=1+(dydx)2−−−−−−−−√=s2+a2−−−−−−√a${\displaystyle \frac{ds}{dx}}\sqrt{1{\displaystyle \frac{dy}{dx}}{}^2}{\displaystyle \frac{\sqrt{s^2{a}^2}}{a}}$
よって，∫dss2+a2−−−−−−√=∫dxa${\displaystyle {\displaystyle \frac{ds}{\sqrt{s^2{a}^2}}}{\displaystyle {\displaystyle \frac{dx}{a}}}}$
左辺の積分計算がめんどくさいので詳細は省略するが，両辺積分して整理する：
s=asinhxa=a(exa−e−xa)2$sa\sinh {\displaystyle \frac{x}{a}}{\displaystyle \frac{a{e}^{\frac{x}{a}}{e}^{\frac{x}{a}}}{2}}$ 
(境界条件は x=0$x0$ で s=0$s0$)
同様に，dsdy=1+(dxdy)2−−−−−−−−√=s2+a2−−−−−−√s${\displaystyle \frac{ds}{dy}}\sqrt{1{\displaystyle \frac{dx}{dy}}{}^2}{\displaystyle \frac{\sqrt{s^2{a}^2}}{s}}$
から，∫sdss2+a2−−−−−−√=∫dy${\displaystyle {\displaystyle \frac{sds}{\sqrt{s^2{a}^2}}}{\displaystyle dy}}$
の両辺を積分して y=a2+s2−−−−−−√$y\sqrt{a^2{s}^2}$ 
以上2式より s$s$ を消去すれば懸垂線の式が得られる。

変分法を用いた導出

こちらの証明方法は高校範囲では理解できないかもしれません。大学の数学で習う「変分法」という汎関数の値を停留させる関数を求める手法を用います。

紐に蓄えられた位置エネルギーは以下の式で表される：
∫mgyds=ρg∫y1+y′2−−−−−−√dx${\displaystyle mgyds\rho gy\sqrt{1y^{\mathrm{\prime }2}}dx}$
よって，f=y1+y′2−−−−−−√$fy\sqrt{1y^{\mathrm{\prime }2}}$ とおいてオイラーラグランジュ方程式を用いるのが筋。
ただし，f$f$ は x$x$ を含まないので，ベルトラミの公式  f−y′∂f∂y′=C$f{y}^{\mathrm{\prime }}{\displaystyle \frac{\mathrm{\partial }f}{\mathrm{\partial }{y}^{\mathrm{\prime }}}}C$ が使える：
y1+y′2−−−−−−√=C${\displaystyle \frac{y}{\sqrt{1y^{\mathrm{\prime }2}}}}C$
上式を整理する：
∫Cdyy2−C2−−−−−−−√=∫dx${\displaystyle {\displaystyle \frac{Cdy}{\sqrt{y^2{C}^2}}}{\displaystyle dx}}$
よって，この式を積分することにより，懸垂線の一般式が得られる：
y=Ccosh(x−AC)$yC\cosh {\displaystyle \frac{xA}{C}}$
特に，x$x$ 軸対称な場合が重要で，そのときには積分定数 A=0$A0$ となり，題意の式を得る。

紐を垂らしたら指数関数が出てくるってなんか感動します！

Tag: オイラーの公式・定理まとめ
Tag: 大学入試で頻出の有名な関数まとめ

分野: 指数・対数関数 　レベル: ★マニアック

オイラーの定理 - Wikipedia
https://ja.wikipedia.org/wiki/%E3%82%AA%E3%82%A4%E3%83%A9%E3%83%BC%E3%81%AE%E5%AE%9A%E7%90%86

オイラーの定理

この項目では、定理について説明しています。eiπ + 1 = 0 については「オイラーの公式」をご覧ください。

• 数論におけるオイラーの定理についてはオイラーの定理 (数論)を参照。
• 剛体の力学におけるオイラーの定理とは、剛体の固定点まわりの回転がその点を通る軸のまわりの回転であらわせるという定理である。
• トポロジーにおけるオイラーの多面体定理（「オイラーの多面体公式」ともいう）
• 数論におけるオイラーの五角数定理、ゴールドバッハ・オイラーの定理
• 微分幾何学におけるオイラーの定理についてはオイラーの定理 (微分幾何学)を参照。
• 三角形におけるオイラーの定理についてはオイラーの定理 (平面幾何学)を参照。

レオンハルト・オイラー - Wikipedia
https://ja.wikipedia.org/wiki/%E3%83%AC%E3%82%AA%E3%83%B3%E3%83%8F%E3%83%AB%E3%83%88%E3%83%BB%E3%82%AA%E3%82%A4%E3%83%A9%E3%83%BC#.E9.96.A2.E9.80.A3.E9.A0.85.E7.9B.AE

ウィキメディア・コモンズには、レオンハルト・オイラーに関連するメディアがあります。

• オイラーの公式
• オイラーの等式
• 数論におけるオイラーの定理
• 微分幾何学におけるオイラーの定理
• 平面幾何学におけるオイラーの定理
• ゴールドバッハ・オイラーの定理
• オイラー予想
• バーゼル問題#オイラーの解法
• オイラー積分
  • ベータ関数
  • ガンマ関数
• オイラー＝ラグランジュ方程式
• オイラーの運動方程式
  • オイラーのコマ
• オイラー力
• オイラー角
• 流体力学におけるオイラーの方程式（非粘性流体）

→ ナビエ-ストークスの式（粘性流体）

• ベルヌーイ・オイラーの仮定
• 座屈応力に関するオイラーの式
• オイラー法
• オイラーの多面体定理
• オイラー円
• オイラー路（オイラーグラフ、準オイラーグラフ）
• オイラー線
• オイラー図
• オイラーのφ関数
• オイラーの和公式
• オイラー積
• オイラーの分割恒等式
• オイラーの五角数定理
• ネイピア数（オイラー数と呼ばれることがある）
• オイラー数
• オイラーの定数
• オイラー標数
• オイラー素数
• オイラー (小惑星)

オイラー＝ラグランジュ方程式 - Wikipedia
https://ja.wikipedia.org/wiki/%E3%82%AA%E3%82%A4%E3%83%A9%E3%83%BC%EF%BC%9D%E3%83%A9%E3%82%B0%E3%83%A9%E3%83%B3%E3%82%B8%E3%83%A5%E6%96%B9%E7%A8%8B%E5%BC%8F

• 編集
• 別の言語で閲覧

オイラー＝ラグランジュ方程式

物理学
ウィキポータル 物理学 執筆依頼・加筆依頼
カテゴリ
物理学 - （画像）
ウィキプロジェクト 物理学

オイラー＝ラグランジュ方程式（オイラー＝ラグランジュほうていしき、英: Euler–Lagrange equation）は汎関数の停留値を与える関数を求める微分方程式である。 オイラーとラグランジュらの仕事により1750年代に発展した。 単に、オイラー方程式、ラグランジュ方程式とも呼ばれる。

ニュートン力学における運動方程式をより数学的に洗練された方法で定式化しなおしたもので、物理学上重要な微分方程式である。 オイラー＝ラグランジュ方程式を基礎方程式としたニュートン力学の定式化をラグランジュ形式の解析力学と呼ぶ。

目次

概要編集

オイラー＝ラグランジュ方程式は、物理学における最大の指導原理の一つである最小作用の原理から導かれる。 これは以下のような原理である： 運動エネルギーとポテンシャルエネルギーの 差（エネルギー保存則の場合は両者の和）をラグランジアンと呼び、 ラグランジアンの時間積分を作用と呼ぶとき、 物理現象は作用を最小化（厳密には極小化）するように動作する。 オイラー＝ラグランジュ方程式は、最小作用の原理を満たす物体の軌跡を変分法で求める事によって導出された方程式である。

最小作用の原理はもともとはニュートン力学（さらにさかのぼれば光学におけるフェルマーの原理）で発見されたものだが、 電磁気学、相対性理論等でも成り立つ物理学の根本的な原理である。 したがってそれらの分野においてもオイラー＝ラグランジュに相当する方程式を立式でき、 その方程式はこれらの分野の基礎方程式（ニュートンの運動方程式、マクスウェルの方程式、アインシュタイン方程式） と等価になる。（ただしこれらの方程式におけるラグランジアンは前述の「（運動エネルギー）－（ポテンシャル）」とは限らない）。 このように最小作用の原理からオイラー＝ラグランジュ相等の式を得るという方針は、様々な基礎方程式に統一的な視点を与える事ができる。

ニュートン力学の場合ラグランジアンをルジャンドル変換する事でハミルトニアン（＝エネルギーに対応する物理量）を得る事ができ、 オイラー＝ラグランジュ方程式をハミルトニアンを使って書き直す事でハミルトンの正準方程式が得られる。 これもニュートン力学における基本的な方程式の１つである。 オイラー＝ラグランジュ方程式や正準方程式で記述したニュートン力学を解析力学という。 なお、ニュートン力学以外の分野の場合、ラグランジアンからハミルトニアン（あるいはその逆）に容易に変換可能であるとは限らない。

また新たな物理学の分野を探求する際、ラグランジアンやハミルトニアンを定義できれば、 そこからオイラー＝ラグランジュ方程式や正準方程式相等の方程式を定式化できる為、 この方程式は未知の領域において基礎方程式を導出する為の強力な道具となる。

一般化座標編集

ニュートンの方程式がデカルト座標を用いて運動を記述する必要があるのに対し、 オイラー＝ラグランジュ方程式は任意の座標（一般化座標）を用いる事ができる。 この点においてもオイラー＝ラグランジュ方程式の方がニュートンの方程式よりも本質的である事が伺える。

またラグランジアンから一般化運動量、一般化力という、運動量と力を一般化した概念が定式化可能で、 これらを用いると、オイラー＝ラグランジュ方程式は一般化力＝（一般化運動量の時間微分）という形にかける。 ニュートンの運動方程式は、力＝（運動量の時間微分）であるので、オイラー＝ラグランジュ方程式は ニュートンの運動方程式を一般化座標に拡張したものと捉える事もできる。

計算上の重要性編集

一般化座標を用いる事ができるという事実は、実際に運動を計算する際有利に働く。 例えば振り子の運動を考える場合、ニュートンの方程式ではデカルト座標を用いねばならない関係上、 縦軸方向と横軸方向の2つの変数を必要とするため式が煩雑になるが、 オイラー＝ラグランジュ方程式の場合は任意の座標系を用いる事ができるため、 振り子の角度に着目する事で、角度という１変数のみで運動を記述でき、より簡単な方程式が立てられる。 （ここでは振り子の長さは一定であると仮定している）。 もちろんニュートン方程式で立式した後極座標に変換すれば同一の式が得られるが、 オイラー＝ラグランジュ方程式の利点はこのような煩雑な変換を施す事なく角度に着目した方程式を最初から直接得られる事にある。

数学における重要性編集

オイラー＝ラグランジュ方程式はシンプレクティック幾何学という、解析力学を起源とする数学の分野でも用いられる。 またリーマン幾何学における測地線方程式は、曲線の長さをラグランジアンとした場合のオイラー＝ラグランジュ方程式である。 なお測地線は相対性理論では光の航路を表すので、これはフェルマーの原理の近代的な定式化になっている。

方程式の詳細編集

以上ではオイラー＝ラグランジュ方程式の物理学的な側面を説明してきたが、方程式そのものは物理学とは無関係に定式化できるので、 まず物理学的な背景から離れて方程式を説明し、その後で方程式のニュートン力学的な解釈を説明する。

C¹ 級関数

${\displaystyle u{\mathbb{R}}^d{\mathbb{R}}^{f}x{x}_1{x}_{d}ux{u}_{1}x{u}_{f}x}$

を考える。

${\displaystyle F{\mathbb{R}}^f{\mathbb{R}}^{fd}{\mathbb{R}}^d\mathbb{R}vmxFvmx}$

としたとき、オイラー＝ラグランジュ方程式とは ${\displaystyle ux}$ に関する以下の連立偏微分方程式のことである。

${\displaystyle \frac{\mathrm{\partial }F}{\mathrm{\partial }{v}_i}ux\mathrm{\partial }uxx\frac{\mathrm{\partial }}{\mathrm{\partial }{x}^{\mu }}\frac{\mathrm{\partial }F}{\mathrm{\partial }{m}_{i\mu }}ux\mathrm{\partial }uxx0i1f}$

ここで ${\displaystyle \mathrm{\partial }ux}$ は x による偏微分

${\displaystyle \mathrm{\partial }ux{\frac{\mathrm{\partial }{u}_i}{\mathrm{\partial }{x}^{\mu }}}_{1if1\mu d}}$

を表す。

なお通常は記号を疎漏に用い、上の方程式を

${\displaystyle \frac{\mathrm{\partial }F}{\mathrm{\partial }{u}_i}ux\mathrm{\partial }uxx\frac{\mathrm{\partial }}{\mathrm{\partial }{x}^{\mu }}\frac{\mathrm{\partial }F}{\mathrm{\partial }{\mathrm{\partial }}_{\mu }{u}_i}ux\mathrm{\partial }uxx0}$

と表記する事が多い。 この表記では F に代入される値としての ${\displaystyle u_i{\mathrm{\partial }}_{\mu }{u}_i}$ が F の変数としての ${\displaystyle v_i{m}_{i\mu }}$ と混用されている。

さらにベクトル表記により f 個の式を一括して

${\displaystyle \frac{\mathrm{\partial }F}{\mathrm{\partial }\mathit{u}}ux\mathrm{\partial }uxx\mathrm{\nabla }\frac{\mathrm{\partial }F}{\mathrm{\partial }\mathrm{\nabla }\mathit{u}}ux\mathrm{\partial }uxx0}$

とも書き表す。

ニュートン力学との関係編集

ニュートン力学においては、関数 ${\displaystyle u_i}$ は一般化座標 ${\displaystyle q_i}$ であり、その変数は時間 t である。一般化座標の次元 f を系の（力学的な）自由度という。

関数 F はラグランジアン L がその役割を果たす。 オイラー＝ラグランジュ方程式は

${\displaystyle \frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_i}qt\stackrel{}{q}tt\frac{d}{dt}\frac{\mathrm{\partial }L}{\mathrm{\partial }{\stackrel{}{q}}_i}qt\stackrel{}{q}tt0}$

となる。なお、ドットは時間による微分を表す。この式を特にラグランジュの運動方程式と呼ぶこともある。

一般化運動量は

${\displaystyle p_{i}qt\stackrel{}{q}tt\frac{\mathrm{\partial }L}{\mathrm{\partial }{\stackrel{}{q}}_i}qt\stackrel{}{q}tt}$

で定義され、これを使うとオイラー＝ラグランジュ方程式は

${\displaystyle {\stackrel{}{p}}_i\frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_i}qt\stackrel{}{q}tt}$

と書き換えられる。上式右辺を一般化力と呼ぶ事にすると、上述の方程式は「一般化運動量の微分＝一般化力」を意味する。

ニュートン方程式は「運動量の微分＝力」であったので、オイラー＝ラグランジュ方程式はニュートン方程式を一般化座標に拡張したものであるとみなす事ができる。

具体例編集

3次元デカルト座標 ${\displaystyle \mathit{x}xyz}$ の場合を考える。 このとき時間微分 ${\displaystyle \stackrel{}{\mathit{x}}\mathit{v}{v}_x{v}_y{v}_z}$ は速度である。 また、ポテンシャルは速度には依らないものとする。

ラグランジアン L は『運動エネルギー - ポテンシャル』の形をしており、

${\displaystyle L\mathit{x}\mathit{v}t\frac{m}{2}{v}_x^2{v}_y^2{v}_z^{2}V\mathit{x}}$

である。

このとき、ラグランジュの運動方程式は

${\displaystyle m\stackrel{}{\mathit{v}}\mathrm{\nabla }V\mathit{x}}$

となり、ニュートンの運動方程式に一致する。

導出編集

汎関数

${\displaystyle Iu{}_{\mathrm{\Omega }}Fux\mathrm{\partial }uxx{d}^{d}x}$

を考える。

オイラー＝ラグランジュ方程式は適当な境界条件の下で汎関数の停留条件 ${\displaystyle \delta Iu0}$ から導かれる。

停留条件を満たす解を ${\displaystyle u\stackrel{}{u}x}$ とする。 積分領域の境界 ${\displaystyle \mathrm{\partial }\mathrm{\Omega }}$ で 0 となる任意の関数 ${\displaystyle \delta x}$を考え、${\displaystyle u_{ϵ}x\stackrel{}{u}xϵ\delta x}$ と書くことにする。 このとき、停留条件は ${\displaystyle I{u}_{ϵ}I\stackrel{}{u}ϵ\delta }$ を ε の関数としてみたときに

${\displaystyle \frac{d}{dϵ}I\stackrel{}{u}ϵ\delta {}_{ϵ0}0}$

である。この微分を計算すると

${\displaystyle \begin{array}{r}\frac{d}{dϵ}\end{array}}$

Iu

ϵδddϵΩ

Fu

ϵδ∂u

ϵ∂δxΩδix∂F∂viuϵ∂uϵx∂δi∂xμx∂F∂miμuϵ∂uϵxdd

x

となるが、被積分関数の第二項を部分積分すると、

${\displaystyle \begin{array}{r}\frac{d}{dϵ}\end{array}}$

Iu

ϵδδix∂F∂miμuϵ∂uϵx∂ΩΩδi

x∂F∂viuϵ∂uϵx∂∂xμ∂F∂miμuϵ∂uϵxdd

x

となる。積分領域の境界 ${\displaystyle \mathrm{\partial }\mathrm{\Omega }}$ で ${\displaystyle \delta x0}$ なので第一項は 0 となる。最終的に、

${\displaystyle \frac{d}{dϵ}I\stackrel{}{u}ϵ\delta {}_{ϵ0}{}_{\mathrm{\Omega }}{\delta }_{i}x\frac{\mathrm{\partial }F}{\mathrm{\partial }{v}_i}\stackrel{}{u}\mathrm{\partial }\stackrel{}{u}x\frac{\mathrm{\partial }}{\mathrm{\partial }{x}^{\mu }}\frac{\mathrm{\partial }F}{\mathrm{\partial }{m}_{i\mu }}\stackrel{}{u}\mathrm{\partial }\stackrel{}{u}x{d}^{d}x0}$

が得られる。 この式が任意の ${\displaystyle \delta x}$ について言えるには、括弧内が 0 でなければならない。 （変分学の基本補題、Fundamental lemma of calculus of variations）

従って、オイラー＝ラグランジュ方程式

${\displaystyle \frac{\mathrm{\partial }F}{\mathrm{\partial }{v}_i}u\mathrm{\partial }ux\frac{\mathrm{\partial }}{\mathrm{\partial }{x}^{\mu }}\frac{\mathrm{\partial }F}{\mathrm{\partial }{m}_{i\mu }}u\mathrm{\partial }ux0}$

が導かれる。

関連項目編集

• ラグランジュ力学
• ラグランジュポイント

ノート