レモン宛書簡より
http://nam-students.blogspot.com/2019/01/leibniz-remond.html
http://nam-students.blogspot.com/2019/01/blog-post_95.html
全集略語
http://leibniz-japan-chrono.seesaa.net/article/115417281.html
デュタン版
https://catalog.hathitrust.org/Record/009345817
https://babel.hathitrust.org/cgi/pt?id=ucm.5315912346;view=1up;seq=543;skin=mobile
1712.04.17 ライプニッツからGoldbach, Christianあて Hannoverより Dut3,437-38
音楽=算数発言あり
クザーヌス
https://nam-students.blogspot.com/2019/01/nicolaus-cusanus1401-1464.html
https://ja.wikipedia.org/wiki/%E3%83%8B%E3%82%B3%E3%83%A9%E3%82%A6%E3%
82%B9%E3%83%BB%E3%82%AF%E3%82%B6%E3%83%BC%E3%83%8C%E3%82%B9
Tools
Opera omnia ... Studio Ludovici Dutens. Tomus Primus [-sextus]
| Main Author: | Leibniz, Gottfried Wilhelm, 1646-1716 |
|---|---|
| Language(s): | Latin |
| Published: | Genevae : apud Fratres de Tournes, 1768. |
| Note: | También disponible diapositiva: DIA 700. |
| Physical Description: | 7 v. ; 4. |
| Locate a Print Version: | Find in a library service is not available from this catalog. Search Worldcat |
Viewability:
- Full viewT. 1 (original from Universidad Complutense de Madrid)
- Full viewT. 2 (original from Universidad Complutense de Madrid)
- Full viewT. 3 (original from Universidad Complutense de Madrid)
- Full viewT. 4,2 (original from Universidad Complutense de Madrid)
- Full viewT. 4,1 (original from Universidad Complutense de Madrid)
- Full viewT. 5 (original from Universidad Complutense de Madrid)
- Full viewT. 6 (original from Universidad Complutense de Madrid)
「相矛盾する性質の結合は許されない」(『ライプニッツの普遍法則』p41)のだから、
火
____/||\____
|乾 _//||\\_ 熱|
||\\/ || \//||
||/\\ || //\||
|// \\||// \\|
/____\||/____\
土 _____ _____ 空気
\\ /||\ //
|\\ //||\\ //|
||\\/ || \\/||
||/\\_||_/\\||
|冷__\\||//__湿|
\||/
水
火(IGNIS)
siccus =乾 calidus=熱
土(TERRA) 空気(AER)
frigida =冷 humida=湿
水(AQVA)
すべて(svmma)ゆるされた(remissa)=共存可能
反対(contraria)
両立可能(combinatio possibilis)
両立不可能(combinatio impossibilis)
象徴要素?(sybolizm fla)
参考: http://www.statemaster.com/encyclopedia/Classical-element
http://blog.livedoor.jp/yoohashi4/archives/51869171.html
(以下同サイトより。「quia ignis est calidus & siccus & aqua frigida & humida.
火は 熱・乾であり、水は 冷・湿であるのだから。」)
いとするならば…」
アリストテレス(Aristotles 前384 - 前322、『二コマコス倫理学』1170a25 ff第9巻第9章、岩波文庫下140頁)
http://en.wikipedia.org/wiki/Cogito_ergo_sum#Predecessors
「…より完全には、〈疑う自己たる、私は思考する、私は存在する、私は思考するもの(レース)である〉である。これは、デカルトが理解していたように、つねに更新されてゆく〈思考の出来事〉である。」
ドゥルーズ(『哲学とは何か』第1章、邦訳37頁)
ドゥルーズ(『差異と反復』第三章、p.170、邦訳210頁)
「〈差異〉は…〈規定作用ソノモノ[私は思考する]〉と〈それが規定するもの[私の存在]〉とのあいだの先験的な〈差異〉として発見される…」
ドゥルーズ(Gilles Deleuze, 1925年1月18日 - 1995年11月4日『差異と反復』第二章、邦訳142頁)
14世紀、フランスのニコール・オレムは加速度運動の解析に成功した(『思想の中の数学的構造』山下正男p205)。
以下の図で,tは時間(extensio-外延量)、距離S割る時間tつまりS/t=vは速度(intensio-内包量)をあらわす。
y
v
| /|
| / |
| / |
| / |
| / |
| / (S) |
| / |
| / |
________|/________| t
| x
|
三角形、S(=1/2vt)の面積で距離を表す(歴史的には微分積分の萌芽だ)。
加速度をaとするとv=atとなり、結局、S=1/2at^2となる。
運動量をmvとすると、運動エネルギーは1/2mv^2であらわされる。
ちなみに、この運動をめぐる認識の差異はライプニッツとデカルト派で論争になった。カントは初期論考
『活力測定考』(1746)でライプニッツ的な形而上学的視点を重視しながらもその不備を指摘することでデカ
ルト派(mv)とライプニッツ(mv^2)の両者を調停しようとしたのだ(多くの研究者はそれが失敗に終わったと考え
ているが)。
(図に話を戻すなら物理量はすべて長さ(S)、時間(t)、質料(m)う3つの次元から掛け算という演算だけで順次組み
「F= ma」と「E=mv^2」
現在、速度vに加速度v=atを加えることで運動量mvと運動エネルギーmv^2の関係は(数式上)説明できる。
しかし、歴史的には運動法則から単純にエネルギーを考える人びとを説得するには長い時間がかかった。
ニュートンの説( 「F=ma」をエネルギーにそのまま適用する説)だと同型トラック二台が正面衝突すると、双方
の車が有していたエネルギーは全て消失したことになる(ボダニス『E=mc^2』邦訳72~5頁。以下は同書の要約)。
しかし、ライプニッツはエネルギーが「増加」すると考えた。消失せず、金属片を跳ね回らせたり…、騒乱はいつまでも
続く…(エネルギー保存の法則)。
デュ・シャトレ夫人(ライプニッツの宿敵ヴォルテールの恋人)が両者の違いに疑問をもったが、彼女が求める証拠
を、その仲間のオランダ人のウィレム・スフラーフェサンデがおこなっていた、重りを柔らかい土の上に落とす実験
の中に見出した。
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgAJVUVrfr5-AiQmsZupri0TQ97ga16RZbTIOcyfJZCx4zSVw4ItyJGqnWNnUh1aurXJluhGqAYp43mUkf7RL3H2KaKweTKOO0mRIipi58PNuEMBsRQvojZGUmPt_Na2y0Hckms/s1600/IMG_02042.jpg
E=mv^1が正しいとすれば、二番目の重りを一番目の二倍の速度で落とす場合、土に沈む深さも二倍になる。速度が
三倍ならば、深さも三倍になるはずだ。が、スフラーフェサンデの得た結果は違った。小さな真鍮の球を、前に落
としたときの二倍の速度で落としたところ、球は土の四倍の深さの穴を作ったのだ。速度を三倍にすると、深さは
九倍になった。
やがて、エネルギーはmv^2に等しいと考えるのが物理学者の常となった。ヴォルテールは恋人の死後にその説(も
ともと宿敵のライプニッツのものなのに)の普及に貢献した。
前述したようにデカルト=ニュートンの説と、ライプニッツの説をカントは調停しようとした(『活力測定考』)。
とはいえライプニッツにも不理解の責任の一端はある。わかり易い論文を書かなかった〜ニュートンの慣性の法則
を取り入れず、潜在的な力を死力、さらに加速度として現性化する力を活力と名付けたが、(形而上学を知的化す
るもので)一般には理解し難かった。
http://yojiseki.exblog.jp/7746386/
14世紀、フランスのニコール・オレムは加速度運動の解析に成功した(『思想の中の数学的構造』山下正男p205)。
以下の図で,tは時間(extensio-外延量)、距離S割る時間tつまりS/t=vは速度(intensio-内包量)をあらわす。
y
v
| /|
| / |
| / |
| / |
| / |
| / (S) |
| / |
| / |
________|/________| t
| x
|
三角形、S(=1/2vt)の面積で距離を表す(歴史的には微分積分の萌芽だ)。
加速度をaとするとv=atとなり、結局、S=1/2at^2となる。
運動量をmvとすると、運動エネルギーは1/2mv^2であらわされる。
ちなみに、この運動をめぐる認識の差異はライプニッツとデカルト派で論争になった。カントは初期論考
『活力測定考』(1746)でライプニッツ的な形而上学的視点を重視しながらもその不備を指摘することでデカ
ルト派(mv)とライプニッツ(mv^2)の両者を調停しようとしたのだ(多くの研究者はそれが失敗に終わったと考え
ているが)。
さて図の説明に戻るなら、vはS^(t-1)であらわされるから結局それらの物理量はすべて長さ(S)、時間(t)、質料(m)とい
う3つの次元から掛け算という演算だけで順次組み立てられている。
山下正男は『思想の中の数学的構造』において、ヘーゲルがこれらを展開しきれなかったと指摘したが、『活力測定考』
以降のカントはこれらを展開し得たと言えるのではないか?
要するに、ライプニッツが指摘したような高い所にある物体の運動エネルギーを換算する作業を、カントは分析論の展開、
つまり「質」の検証の中で行っていると言えるのだ。
「F= m a」と「E=mv^2」
現在、速度vに加速度v=atを加えることで運動量mvと運動エネルギーmv^2の関係は(数式上)説明できる。
しかし、歴史的には運動法則から単純にエネルギーを考える人びとを説得するには長い時間がかかった。
ニュートンの説( 「F= m a」をエネルギーにそのまま適用する説)だと同型トラック二台が正面衝突すると、双方
の車が有していたエネルギーは全て消失したことになる(ボダニス『E=mc^2』邦訳74−5頁。以下は同書の要約)。
しかし、ライプニッツはエネルギーが増加?すると考えた。消失せず、金属片を跳ね回らせたり…、騒乱はいつまでも
続く…(エネルギー保存の法則)。
デュ・シャトレ夫人(wiki、ライプニッツの宿敵ヴォルテールの恋人)が両者の違いに疑問をもったが、彼女が求める証拠
を、その仲間のオランダ人のウィレム・スフラーフェサンデ(en:wiki)がおこなっていた、重りを柔らかい土の上に落とす実験
の中に見出した。
E=mv^1が正しいとすれば、二番目の重りを一番目の二倍の速度で落とす場合、土に沈む深さも二倍になる。速度が
三倍ならば、深さも三倍になるはずだ。が、スフラーフェサンデの得た結果は違った。小さな真鍮の球を、前に落
としたときの二倍の速度で落としたところ、球は土の四倍の深さの穴を作ったのだ。速度を三倍にすると、深さは
九倍になった。
やがて、エネルギーはmv^2に等しいと考えるのが物理学者の常となった。ヴォルテールは恋人の死後にその説(も
ともと宿敵のライプニッツのものなのに)の普及に貢献した。
デカルト=ニュートンの説と、ライプニッツの説をカントは調停しようとした(『活力測定考』)。その考察は
ライプニッツを貶めるものだったが、それはカントがライプニッツを理解しなかったためである。
とはいえライプニッツにも不理解の責任の一端はある。わかり易い論文を書かなかった〜ニュートンの慣性の法則
を取り入れず、潜在的な力を死力、さらに加速度として現性化する力を活力と名付けたが、(形而上学を知的化す
るもので)一般には理解し難かった。
参考:
NHK高校講座
http://www.nhk.or.jp/kokokoza/tv/butsuri/archive/resume025.html
http://www.nhk.or.jp/kokokoza/tv/butsuri/archive/resume035.html
Newton's Laws - Second Law
http://www.youtube.com/watch?v=PF5zxdg9N5s
上記の模索の歴史は以下のアインシュタインが1905年に提唱した方程式にも繋がっていく。
Einstein's Proof of E=mc²
(質料は凝縮されたエネルギーの究極の形である…)
http://www.youtube.com/watch?v=hW7DW9NIO9M
F = m aは無限に拡大できるわけではない。どんなに加速しても光速を超えられない。
https://m-repo.lib.meiji.ac.jp/dspace/bitstream/10291/14240/1/isumiakyouyodezain_3_105.pdf
一六七九年一二月一日にホイヘンスに宛ててかれはなんと書いたか。それはつぎのような
ものである。「わたしはあなたが、故スピノザ氏の本を念入りにお読みになったかどうか
を知りたい。かれの証明なるものはきわめて厳密というわけにはいきません。たとえば、
神だけが実体であるとか、その他の事物は神的本性の様態であるといったことをかれが言
うときにそうです」。 かれがべつのところで書いたもののなかに、われわれは、もっと
も短いが同時にもっとも激しい判断を見いだす。その判断は、かれの同時代人の一人によ
ってもたらされたもので、つぎのことばのなかに込められている。すなわち、「『エチカ、
あるいは、神について』、驚くほど欠陥にみちた書物」。 一八五三年一〇
月二五日ハノーファにて
参考:
http://books.google.co.jp/books?id=PXEZc30z3BQC&pg=PA216&lpg=PA216&
『学の形成と自然的世界―西洋哲学の歴史的研究』 (1941年)
三宅剛一 p.403
- ライプニッツの落書き
Stephen Wolfram Blog : Dropping In on Gottfried Leibnizhttps://blog.stephenwolfram.com/2013/05/dropping-in-on-gottfried-leibniz/https://blog.stephenwolfram.com/data/uploads/2013/05/29-large-a.png
RT @asonosakan: ハノーファーにあるライプニッツ・アーカイブから、彼の手稿を覗き見。スピノザと思われる落書きが笑えるww 流石万学の天才は絵も上手い。スピノザだという根拠はないが
ゲーデルの不完全定理の解説で一番解りやすいのは僕の知る限り、『はじめての現代数学』(瀬山士郎著)のそれだった。
以下引用です。
内容
| 1, 2, ・・・, n, ・・・
___|____________________
f1(y)|f1(1) f1(2) ・・・ f1(n) ・・・
f2(y)|f2(1) f2(2) ・・・ f2(n) ・・・
・ |・ ・ ・ ・
・ |・ ・ ・ ・
・ |・ ・ ・ ・
fn(y)|fn(1) fn(2) ・・・ fn(n) ・・・
・ |・ ・ ・ ・
・ |・ ・ ・ ・
・ |・ ・ ・ ・
¬は否定だから最後につけ加えればよいから、ヨxP(x,n,n)について考えてみよう。これは、「ゲーデル数がnである一変数 y を含む命題(すなわちfn(y) )の変数 y に数nを代入した命題の形式証明のゲーデル数となる x が存在する」という内容を持ち、したがって¬∃xP(x,n,n)はこれの否定、すなわち繰り返しを嫌わずに書けば「ゲーデル数がnである一変数 y を含む命題の変数yに数nを代入した命題の形式証明のゲーデル数となる x が存在しない」となる。
ところが、ゲーデル数nを持つ一変数を持つ一変数yを含む命題とは fn(y)のことであり、fn(y)とはすなわち¬ヨxP(x,y,y)であった。すなわち上の文章を簡単に書けば,「¬∃xP(x,n,n)の形式証明は存在しない」ということで「¬∃xP(x,n,n)は証明できない」ということになる。ところが、この「 」内の命題こそ¬∃xP(x,n,n)に他ならない!
ついにわれわれは「この命題は証明できない」のきちんとした数学的表現を入手すること に成功したのである。
(略)
ここで用いられた論法が一種の対角線論法であることに十分注意を払ってもらいたい。一変数の命題をすべて一列に並べ、f1(y) ,f2(y) ,・・・とし f1(1) , f1(2) ,・・・f n(n),・・・を考察するというのはまさしく対角線論法そのものである。カントールによって集合の階層構造を引き出すために考案された対角線論法は,集合論内のパラドックスと絡まりあいながら、ゲーデルによる決定不能命題の発見という20世紀数最高の結果の一つを生み出すにいたったのである。
(以上、『はじめての現代数学』瀬山士郎著、講談社現代新書p161-163より。早川文庫より復刊)
瀬山氏は対角線論法の後に不完全性定理のもうひとつの肝であるゲーデル数(ゲーデルによる素因数分解を使ったコード化)について説明している。
本題は、(瀬山氏も触れいてないのだが)このゲーデル数のアイデアがライプニッツの結合法論そのものであるということだ。
これはあまり言及されないが、もっと知られていい。
「われわれはその事物によって他の事物を表示するために素数を使用するのである。」
(『普遍的記号法の原理』Elementa Characteristicae universalis ,1679「計算の原理」1679、邦訳ライプニッツ著作集1、64−5頁より)
ゲーデルは生前,ライプニッツ研究ばかりしている時期があって友人のエルデシュに怒られたこともあるようだが(「君が学者になったのは皆が君の研究をするためであって、君がライプニッツの研究をするためではない」)、ゲーデルの功績は先人の研究を受け継いだものでもあったのだ。
カントール(対角線論法)×ライプニッツ(結合法論)=ゲーデル(不完全性定理)
ということになるだろうか。
ちなみに、 ライプニッツ再評価はどう考えてもラッセルの『ライプニッツ研究』が重要な位置を占めている。 復刊が待たれる。
☆
http://russell-j.com/cool/03T-PREF.HTM
何故に彼は,モナドが,相互に作用し得ないと考えたか,如何にして識別し得ざるものの同一性を信ずる様になったか,充足理由の法則によって彼は何を意味するか――これらのみならず他の多くの疑問はどうしても解かねばならぬものと考えられたが,然し何もわからなかった。私は――多くの他の人達が感じている如く――モナド論は,恐らく筋道が通っているが然し,全く勝手な,お伽噺の一種であると感じたのである。この点に関して私は,「形而上学叙説」及びアルノー宛の手紙を読んだ。俄に一条の光が,ライプニッツの哲学的大建築物のあらゆる最奥の隅々に投げられたのである。私は,大建築の基礎がどの様にすえられているか,その上,如何にして,その基礎から大建築の上部構造が視界に現われてくるかを見た。この表面上は気まぐれな体系も二三の簡単な前提から演繹されうるものであり,それらの前提は,それらからライプニッツが引き出した結論を除けば,大低の哲学者でなくても,相当数の哲学者は,喜んで承認していたであろうと思われる。私に光明を投じたと思われる箇所は,他の人々にもやはり,その様に考えられるであろう事を望む事は,まんざら理由なきにしもあらずと思われる。
解析の元祖だから誤解されているがライプニッツのモナドは離散数学と親和性がある。
ドゥルーズはうまく説明している。
《ライプニッツは、欺かない神についてのデカルトの推論をかなり警戒し、これに不共可能性の
水準で新しい根拠を与えている。神は戯れるが、戯れの規則を与えるのだ(略)。この規則とは可
能世界は神が選んだ世界と不共可能的ならば、存在にたどりつくことがないということだ。ラ
イプニッツによれば*『アストレー』のような小説だけが、われわれにこのような不共可能的
(incompossible)なものの理念を与えるのである。》
(ドゥルーズ『襞 ライプニッツとバロック』邦訳単行本 110頁)
*(Lettre a Bourguet,decembre 1714)未邦訳
オノレ・デュルフェ作の『アストレ(ー)』は17世紀パリの貴婦人に流行ったロマン小説で、日本
では無名だが、今度エリック・ロメールによって(小説の一部が)映画化され2009年に公開された。
http://youtu.be/0JRwGGndvyk (日本語字幕つき予告編)
可能世界なるものがデカルトのような推論によって「本質」に回収されるのを嫌ったライプニッツが
小説(しかもラブストーリー)を念頭においていたというのは面白い。
ちなみにフーリエは『アストレ』からセラドニーCeladonieという概念を抽出し展開している。この
造語は精神的ないし感傷的な恋愛情念を意味するらしい。その精神的愛はフーリエの唱える共同体
では重要度を増すという。
ロメールの遺作『我が至上の愛 アストレとセラドン』ダイジェスト
ロメールの遺作『我が至上の愛 アストレとセラドン』
https://nam-students.blogspot.com/2018/12/blog-post_5.html
村上俊江 「ライブニッツ氏と華厳宗」 1896年
でライプニッツと華厳宗の類似例として引用参照されたのは以下(村上はドイツ語で引用)、
モナドロジー
http://nam-students.blogspot.jp/2013/10/blog-post_1.html#note65
65.そして自然の創作者は、この神的な、限りなく驚嘆すべきわざを
ふるうことができた。なぜなら、物質のどの部分も、昔の人が認めたように無限に分割が
可能であるばかりでなく、各部分は実際にさらに多くの部分へと限りなく細分さ
れていて、その部分のどれもが固有の運動をしているからである。さもなけれ
ば、物質の各部分が宇宙を表出することは不可能であろう。
66. そこで、物質のどんな小さい部分にも、被造物の、生物の、動物の、エンテレケイアの、
魂の世界が認められる。
67. 物質のどの部分も植物に満ちた庭とか、魚でいっぱいの池のようなものと考えることが
できる。ただし、その植物のどの小枝も、動物のどの肢も、その体液のどの一滴も、やはり
同じような庭であり池なのである。
68. そして、庭の植物のあいだにある地面や空気、池の魚のあいだにある水は、植物や魚で
はないけれども、じつはやはり植物や魚を含んでいる。ただ、それらがあまりに微細なので、
ほとんどの場合われわれには見えない。
[華厳経に関しては漢文で引用、]
一一微塵中、見一切法界(華厳経第4巻)
以一仏土満十方、十方人一、亦無餘。(同上)…
遍満一切諸法界、一切毛孔自在現。(華厳経第3巻)
https://digital.slub-dresden.de/werkansicht/dlf/60594/1/
http://digital.slub-dresden.de/fileadmin/data/358423678/358423678_tif/jpegs/358423678.pdf
その口絵に引用された変身物語、
https://la.m.wikisource.org/wiki/Metamorphoses_(Ovidius)/Liber_XII
Det mihi se: faxo, triplici quid cuspide possim, Sentiat.
《やつがわたしの領分までやって来さえすれば! そうすれば、この三つ叉の鉾の威力を
思い知らせてやれように。》
オウィディウス『変身物語』巻12岩波文庫下186頁
間に挟まれたad Zoilumは正確にという意味か?
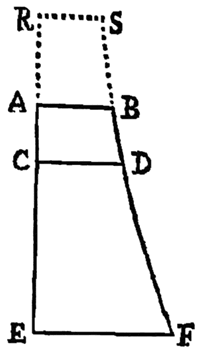
口絵がどこまでライプニッツの意図を反映しているかはわからないが(本文にはアエネイス、
変身物語への言及はない)結合法論的志向が興味深い。真ん中の三角形は回転するのではないか?
その三角内の構成=「暗黙→媒介→究極」はやはり見れば見るほどヘーゲル=「意識→対他→
絶対精神」に似ている。
ヘーゲルはライプニッツのこの著作を知っていただろうが、ケインズが受け継ぐことになる
確率論的な部分は重視しなかった
絶対精神は確率論を排除するからだ
ラッセルの形式論理学ならば演繹的推論を用い、は0(否)か1(是)かである。けれども我々の日常生活は、
そのように確実ではない判断に満ちている。
ケインズ『確率論』(1921)の帰納的推論は、日常の推論に相当する0<a/h<1の合理的信念を扱う。
ケインズは(ニュートンを支持していたが)ライプニッツを意識していたと思う。
右下から悟性に光が差し込む??ということらしい。
ピタゴラスみたいな図で已然神秘主義的だが、ライプニッツは結合法論のように、身体と精神とのいろいろな組み合わせを想定しているのではないだろうか?








[91]
ショーペンハウアー『意志と表象としての世界』(西尾幹二訳、中央公論社)から。
<……音楽はあれこれの個々の、特定の喜びとか、あれこれの悲哀とか、苦痛とか、驚愕とか、歓喜とか、愉快さとか、心の安らぎとかを表現しているわけではけっしてない。音楽が表現しているのは喜びというもの、悲哀というもの、苦痛というもの、驚愕というもの、歓喜というもの、愉快というもの、心の安らぎというものそれ自体なのである。>(484-5頁)
<もしも音楽を完全に正しく微に入り細にわたってくまなく説明することに成功したとすれば、いいかえれば音楽が表現するところを概念を用いて詳細に再現することに成功したとしたら、それはそのまま世界というものを概念を用いて十分に再現し説明したことにもなるのであって、同じことを別様にいえば、これこそ真の哲学になるのだといえるであろう。したがって先に引用したライプニッツの言葉[音楽は無意識的な算数の練習である。その際自分がいま計算していることを精神は知らないでいる。]は、比較的低い立場で見ればあれなりに正しいわけであったが、いまわれわれの比較的高い音楽観の与える意味でいえば、次のようにパロディー化して言い替えることができる。「音楽は無意識的な形而上学の練習である。その際自分がいま哲学していることを精神は知らないでいる」(略)われわれはいま、互いに異なるが、両方ともに正しい二つの音楽観(訳者注:ライプニッツの音楽観と、ショーペンハウアーの音楽観)を一つに合わせてみれば、ピュタゴラス派の数哲学とか、「易経」にみられるシナ人の数哲学のような、なにかしら数に関する哲学の可能性を理解できるにいたるであろう。>(489-90頁)
http://www.eonet.ne.jp/~orion-n/ESSAY/TETUGAKU/10.html
Musica est exercitium arithmeticae occultum nescientis se numerare animi.
Music is a hidden arithmetic exercise of the soul, which does not know that it is counting.
Letter to Christian Goldbach, April 17, 1712.
Arthur Schopenhauer paraphrased this quotation in the first book of Die Welt als Wille und Vorstellung: Musica est exercitium metaphysices occultum nescientis se philosophari animi. (Music is a hidden metaphysical exercise of the soul, which does not know that it is philosophizing.)
http://en.wikiquote.org/wiki/Gottfried_Leibniz
http://en.wikiquote.org/wiki/Gottfried_Leibniz
Musica est exercitium arithmeticae occultum nescientis se numerare animi.
Music is a hidden arithmetic exercise of the soul, which does not know that it is counting.
Letter to Christian Goldbach, April 17, 1712.
Arthur Schopenhauer paraphrased this quotation in the first book of Die Welt als Wille und Vorstellung: Musica est exercitium metaphysices occultum nescientis se philosophari animi. (Music is a hidden metaphysical exercise of the soul, which does not know that it is philosophizing.)
ショーペンハウエルが引用した
...
正意志3:52
ライプニッツの言葉[音楽は無意識的な算数の練習である。その際自分がいま計算していることを精神は知らないでいる。]
http://www.sanynet.ne.jp/~norio-n/ESSAY/TETUGAKU/10.html
参考:
(ライプニッツ『結合法論』(邦訳著作集1などに抄訳所収)扉に採用された