新しい金融論―信用と情報の経済学 スティグリッツ他、Towards a New Paradigm in Monetary Economics -Stiglitz
http://nam-students.blogspot.jp/2016/02/towards-new-paradigm-in-monetary.html
http://nam-students.blogspot.jp/2015/09/blog-post_34.html
ローマー『上級マクロ経済学』(Advanced Macroeconomics,David Romer)1996~:目次
http://nam-students.blogspot.jp/2015/04/advanced-macroeconomicsdavid-romer.html
マーケット・デザイン
https://nam-students.blogspot.com/2019/01/blog-post_14.html
http://nam-students.blogspot.jp/2016/03/blog-post_34.html(本頁)
マッチング理論:再考
https://nam-students.blogspot.com/2019/01/blog-post_4.html
世代重複モデル:再考
http://nam-students.blogspot.com/2018/10/overlappinggenerationsmodel.html
ゲーム理論で解明されたユダヤの知恵
http://nam-students.blogspot.jp/2012/11/blog-post_28.html
フェルプス 2006
https://nam-students.blogspot.com/2019/03/edmund-s-phelps-statistical.html
森嶋通夫 Michio Morshima
http://nam-students.blogspot.com/2018/09/michio-morshima.html
(森嶋はサーチ理論を開発した経済学者のひとりであるピサリデスを指導した)
http://okmtnbhr.seesaa.net/article/166452317.html
+
(取引機会を得る確率)
×
(取引成立の価値 または サーチ継続の価値)
日経ビジネス2009.7.27.89頁 より
2010年10月21日
ジョージ・スティグラー
https://en.wikipedia.org/wiki/George_Stigler
https://ja.wikipedia.org/wiki/%E3%82%B8%E3%83%A7%E3%83%BC%E3%82%B8%E3%83%
BB%E3%82%B9%E3%83%86%E3%82%A3%E3%82%B0%E3%83%A9%E3%83%BC
ジョージ・ジョセフ・スティグラー(George Joseph Stigler、1911年1月17日 - 1991年12月1日)は、アメリカ合衆国の経済学者。1982年にノーベル経済学賞を受賞した。
- スティグラーは産業組織論や経済学史を主領域として研究を行っていた。スティグラーは産業組織論において、20世紀前半の主流派であったハーバード学派に対抗して、市場構造の集中度の高さが必ずしも市場の非効率性につながらないことなどを示した。また従来は価格と経済という現象にのみ適用されていた新古典派経済学をゲーリー・ベッカーとともに拡張し、あらゆる行動は合理的に選択されているという点を示したことでも有名である。
- また本来は消費者保護のためであったはずの規制が、いつの間にか生産者保護のための規制に転換してしまうという現象(規制の虜)のメカニズムを明らかにした。スティグラーはこの見地から、規制よりも市場構造に重点を置いた政策を支持する主張を行った。
- スティグラーはミルトン・フリードマンと並ぶシカゴ学派の重鎮であり、1982年には市場と規制に関する研究が評価され、ノーベル経済学賞を受賞した。また1987年には、アメリカ国家科学賞も授与されている。
日本語訳著書
サーチ理論wikiより
《ジョージ・J・スティグラーは商品売買における情報や職業の探索を重要な問題だと提唱し[1][2]、ジョン・J・マッコールは最近の仕事に基づいたoptimal stopping理論をベースにして、動的な職業探索のモデルを提唱した[3][4][5]。マッコールの論文では、選択肢が完全情報的で不変、また貨幣の価値が不変であるとき、職業提供者が失業者に対して仕事を提供するか否かについて研究がなされている[6]。》
- ^ Stigler, George J. (1961), 'The economics of information'. Journal of Political Economy, 69 (3), pp. 213-25.
- ^ Stigler, George J. (1962), 'Information in the labor market'. Journal of Political Economy, 70 (5), Part 2, pp. 94-105.
- ^ D. Mortensen (1986), 'Job search and labor market analysis'. Chapter 15 of The Handbook of Labor Economics, vol. 2, edited by O. Ashenfelter and D. Card.
- ^ R. Lucas and N. Stokey (1989). Recursive Methods in Economic Dynamics, pp. 304-315.
- ^ J. Adda and R. Cooper (2003), Dynamic Economics: Quantitative Methods and Applications, p. 257.
- ^ McCall, John J. (1970), 'Economics of information and job search'. Quarterly Journal of Economics, 84, pp. 113-126.
《近年、マッチング関数という枠組みを用いて、就職活動をはじめとした様々な探索がマクロ経済学のモデルに組み入れられつつある。 ピーター・ダイアモンド、デール・モーテンセン、クリストファー・ピサリデスの3人はマッチング理論の功績を称えられ2010年のノーベル経済学賞を受賞した。
労働経済学でのマッチングのモデルでは、2つのタイプの探索が相互作用する。すなわち、新しい仕事の形成は、労働者の探索における意思決定と、会社の求人を出す意思決定との2つに依存するとしている。マッチングモデルには賃金格差についても扱うものもあるが[10]、それを無視して簡素化されたモデルでは、仕事を始める前にランダムな長さの失業期間が生まれてしまうことのみを表現している[11]。》
- ^ Mortensen, Dale, and Christopher Pissarides (1994), 'Job creation and job destruction in the theory of unemployment'. Review of Economic Studies, 61 (3), pp. 397-415.
- ^ Pissarides, Christopher (2000), Equilibrium Unemployment Theory, 2nd ed. MIT Press, ISBN 0262161877.
スティグリッツが近著でサーチ理論を絶賛している(「過去数十年で経済理論に生じた重要な進歩のひとつは..."サーチ理論"だ」『新しい教科書』2016邦訳245頁)。シャピロ=スティグリッツ・モデルでも表されていたが、不完全な労働市場(さらに離散的なそれ)はスティグリッツのいう情報の非対称性を前提にしたものだ。
| 年 | 受賞者名 | 国籍(出身国) | 受賞理由 | |
|---|---|---|---|---|
| 2010年 |  | ピーター・ダイアモンド | 労働経済における サーチ理論に 関する功績 | |
 | デール・モーテンセン | |||
 | クリストファー・ピサリデス | ( | ||
サーチ理論
https://ja.wikipedia.org/wiki/%E3%82%B5%E3%83%BC%E3%83%81%E7%90%86%E8%AB%96
ミクロ経済学において、サーチ理論(さーちりろん、英語:search theory)は即座に取引相手を見つけることができず、そのために商取引の前にパートナーを捜し求めなければならないような売り手や買い手についての研究である。探索理論とも呼ばれる。
サーチ理論は経済学の多くの領域で利用されている。労働経済学においては、労働者の就職活動において起こる摩擦的失業を説明するために用いられてきた。消費者行動分析で は、購買決定を分析するために用いられてきた。労働者の観点から考えて引き受けられやすい仕事というのは、賃金が高く、望ましい利益を提供してくれ、快適 で安全な労働環境の下で働けるものであり、 消費者の観点から考えて購入されやすい商品というのは、価格が安く、高い品質を持っているものだろう。いずれの場合にしろ、仕事や商品が受け入れられるか どうかは、市場にある代替品について探索する人が持っている考えに依存している。
より厳密な意味で言うと、サーチ理論は、選択の遅れによって損失を被る状況下で価値がそれぞれ異なる複数の選択肢がある時、個人の最適な選択を行う ことを目的としている。 探索モデルは再選択を行った時の価値と、選択の遅れによる損失のバランスを釣り合わせる最も良い均衡点を示すものである。 数学的には、optimal stopping(最適な妥協点)を見つけだすために使われる。
マクロ経済学者はこのサーチ理論を一般均衡モデルにまで拡大し、マッチング理論*またはサーチ・マッチング理論と呼ばれている。
*参考:
Who Gets What(フー・ゲッツ・ホワット) ―マッチメイキングとマーケットデザインの新しい経済学 Kindle版
https://www.amazon.co.jp/dp/B01D1D3XTC
失業率の決定
求人率(V)
|
| o
| /
| o / 有効求人倍率
| /
| o /
|____/
| /o
| / | o
| / | o o ベバリッジ曲線
|/___|___________
失業率(U)
(政府の失業対策が功を奏すれば、ベバリッジ曲線(Beveridge Curve:定常状態における失業率Uと求人率Vの関係を表したもの)は全体が左にズレ込む。
労働市場サーチ理論 今井亮一
http://www.jil.go.jp/institute/zassi/backnumber/2012/04/pdf/016-019.pdf
Mortensen-Pissarides モデル(MP モデル)...
MP モデルは,複雑な設定から出発して,最終的に2 つの式から2 つの未知数を決めるという,ほとんど中学校の数学のような簡潔な世界に到達する。ここで
2 つの未知数とは,有効求人倍率と,「雇用関係解消を決める閾値(しきいち)生産性」である...
Mortensen-Pissarides モデル(MP モデル):
|
| 雇用喪失条件(JD)
| \ /
| \ /
閾値_|____\/
生産性| /\
| / |\
| / | \雇用創出条件(JC)
|_____|______
有効求人倍率
Mortensen-Pissarides モデル(MP モデル):
| 雇用喪失条件(JD)
| \ /
| \ /
| \ /
閾値 |ーーーーーX
生産性| /|\
| / | \
| / | \雇用創出条件(JC)
|_____|______
有効求人倍率
右上がりのJD 条件と右下がりのJC 条件が交差す るところで,サーチ均衡の閾値生産性と有効求人倍率 が得られる。この2 つさえ決まれば,その他の大事な 変数(賃金や失業率)が,副産物として自動的に決 まってくる再帰的(recursive)な構造になっている。 これがMP モデルの高い操作性の所以である。
例えば,解雇規制の効果を考えよう(図4)。規制が,割増退職金などの労使間の所得移転にとどまっている限り,解雇規制は,有効求人倍率や失業率に影響を与えないとされるが,これはMPモデルでも確認できる。他方,解雇規制が実物費用,例えば,法手続きや解雇予告期間義務をともなう場合であれば,閾値生産性が低下し,雇用がより起こりにくくなる一方,有効求人倍率はそれほど変化しない。このような解雇規制は,解雇さえしなければ企業に負担は生じないという意味での一種の雇用助成金であり,企業の参入を促す反面,失業者が供給されないので,求人を出してもなかなか充足されず,最終的に参入のメリットが帳消しになるからである。有効求人倍率が変化しなければ,失業率も変わらない。
図4 解雇規制の効果
閾値生産性雇用喪失条件(JD)雇用創出条件(JC)有効求人倍率
他方,失業保険の効果はもっと明快である(図5)。保険料を引き上げても給付を増やしても,閾値生産性が上昇し解雇は起こりやすくなり,有効求人倍率が低下し,失業率が増える。保険料の引き上げは雇用への課税であるし,給付を増やせば労使も安心して雇用関係解消で合意できることを考えれば,この結果は自然である。
図5 失業保険料・給付の効果
閾値生産性雇用喪失条件(JD)雇用創出条件(JC)有効求人倍率
Ⅱ サーチ摩擦(searchfriction)のミクロ的基礎づけ通常,
サーチ理論では,労働者と企業の「出会い関数(matching function)」というものを仮定し,その上に体系的な市場モデルを構築する。すなわち,サー チ摩擦の実体を特定せず,とりあえずブラック・ボッ クスとしておいて,それ以外の部分を整合的に構成す るのである。しかし,近年は,このサーチ摩擦そのも のを,企業や労働者の最適化行動からモデル化しよう という研究が盛んである。こういう方向の研究は, 「指向的サーチ(directed search)」の研究と呼ばれる。
参考:
http://homepage.ntu.edu.tw/~yitingli/file/macro%20and%20money/Aggregate%20Demand%20Management%20in%20Search%20Equilibrium.pdf
www.amazon.co.jp/dp/4130402358
Pissarides, Christopher (2000), Equilibrium Unemployment Theory, 2nd ed. MIT Press, ISBN 0262161877.
http://www.amazon.com/Equilibrium-Unemployment-Theory-2nd-Edition/dp/0262161877
http://www.amazon.co.jp/Equilibrium-Unemployment-Theory-Press/dp/0262161877/
- OLGモデル(Overlapping Generations Model)の発展(1965年)。
- ダイアモンド=ミルレス定理(総生産効率性定理)の導入(1971年)。
- サーチ理論(サーチ・アンド・マッチング理論)では、求人が十分にあるのに大量の失業者が存在する「雇用のミスマッチ」などをうまく説明できるようになった(1982年)。(この理論により、ノーベル経済学賞を受けた。)ダイアモンドは、ワルラスの一般均衡的取引ではなく、売り手と買い手がばらばらに取引する場合、需要があっても取引が成立しないとして、そうした「局所的・分権的取引」を数学的に分析した。(その後、デール・モーテンセンとクリストファー・ピサリデスが労働市場に適用した。)
- サーチ理論としては、住宅取引、貨幣理論、公共経済学、家族経済学など広い分野に応用されている。
- また、社会保障論の専門家である。
http://homepage.ntu.edu.tw/~yitingli/file/macro%20and%20money/Aggregate%20Demand%20Management%20in%20Search%20Equilibrium.pdf
c*
|
| de/dt=0
y| o
| o
| o o @ o dc/dt=0
| o o A
| o o
|o @ o o
| o B
|________________e
0 1
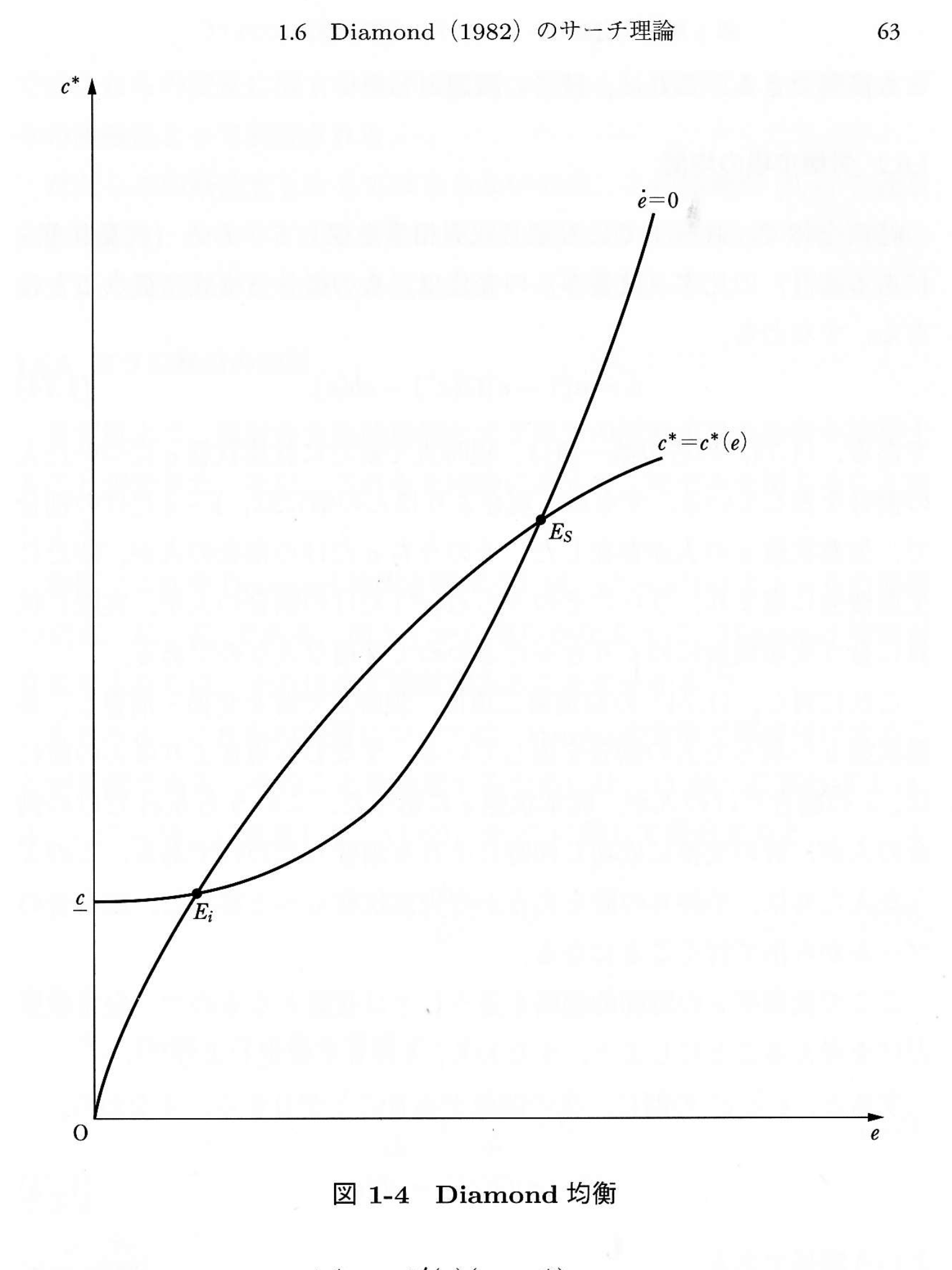
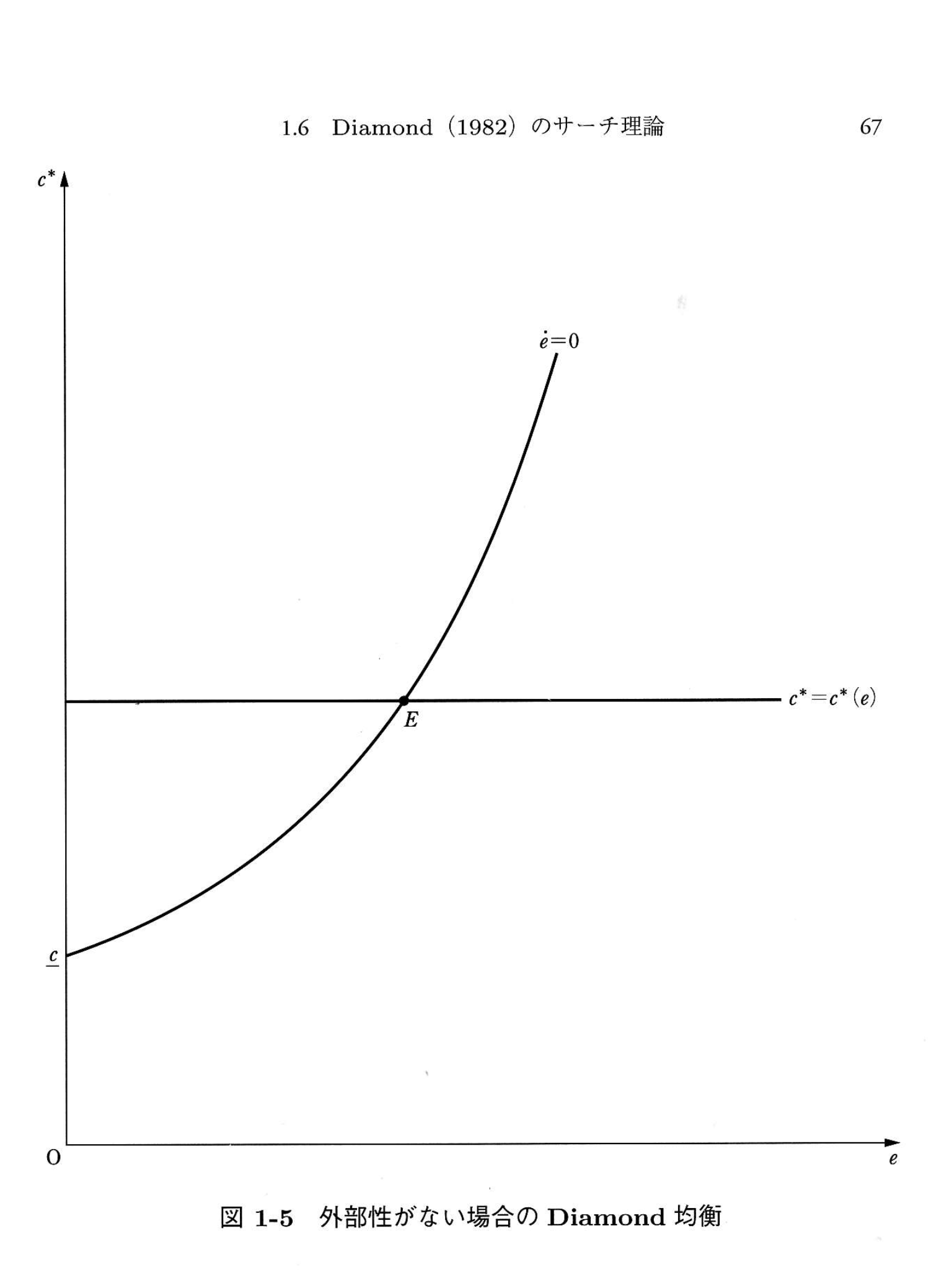
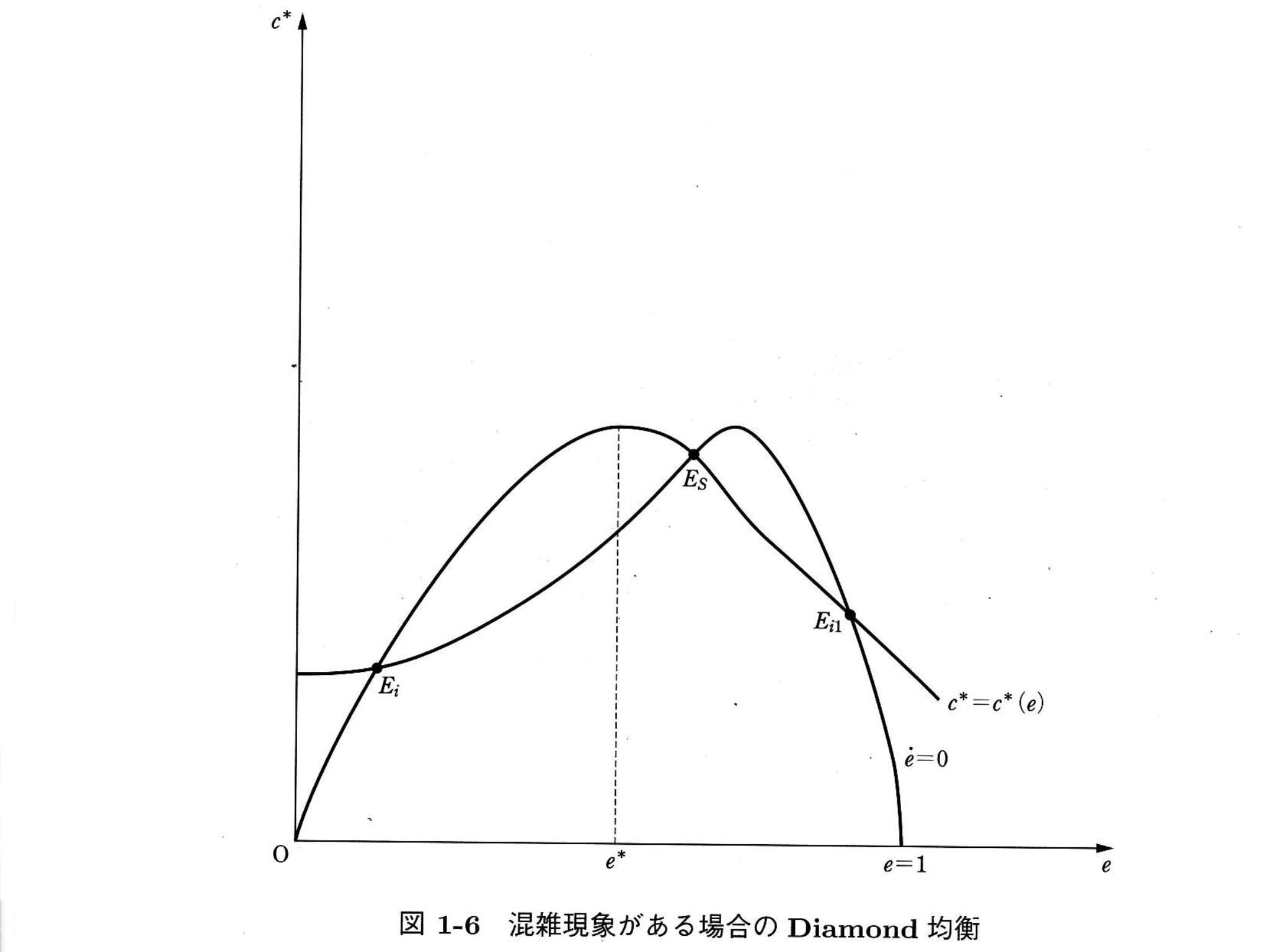
cは生産に要する努力。eは雇用率。均衡点はAB二つある。
Aggregate Demand Management in Search Equilibrium. Peter A. Diamond. Massachusetts Institute of Technology. Equilibrium is analyzed for a simple barter model with identical ... [Journal of Political Economy, 1982, vol. 90, no. 5]
http://homepage.ntu.edu.tw/~yitingli/file/macro%20and%20money/Aggregate%20Demand%20Management%20in%20Search%20Equilibrium.pdf
ノースウェスタン大学教授を長く務めるとともに研究を行った。専門は労働経済学、マクロ経済学である。2010年、ピーター・ダイアモンドとクリストファー・ピサリデスと共に、労働経済におけるサーチ理論に関する功績を称えてアルフレッド・ノーベル記念経済学スウェーデン国立銀行賞を授与された。アメリカ経済学会会員、計量経済学会会員、経済動学学会会員、労働経済学会員であった。
- 彼は、摩擦的失業の「サーチおよびマッチング理論」に対する先駆者として特に有名である。労働移動と再配分、調査と展開、および個人的関係を研究するためにこの理論から洞察を広げていった。
- モーテンセンはピーター・ダイアモンドのサーチ理論を労働市場に用いて進展させ、求職者はより良い職場を 雇用者はより良い労働者を求めるため、互いに多数の相手と接触することになり、「最適のマッチングを発見すること」が非常に困難になる。そのことが大量の求職があるにもかかわらず失業者が増加する状態を生むとしている。これはノーベル賞受賞者3人の頭文字からDMPモデルと呼ばれている。また、失業保険が充足すればするほど、失業者がよりよい職を求めるゆとりができるため、失業期間が長期化するとの考えも示している[2][3]。
- 2011年2月には中国経済の見通しについて述べ、大量の安価な労働力を長所として世界最大の輸出国となったが、この長所は永久に続くわけではない。今後は労働者の教育、技術水準の向上、ハイテク産業への投資などに力を注ぐことが発展の継続の要点となると指摘した。また、人手不足の解消については政府の賃上げ抑制を批判し、補助金を支出するなどして労働力過多地域に企業移転を勧めていくべきとの考えを示している[4]。
D. Mortensen (1982), 'The matching process as a non-cooperative/bargaining game.' In The Economics of Information and Uncertainty, J. McCall, ed., NBER, ISBN 0-226-55559-3.
http://www.nber.org/chapters/c4437.pdf
(サーチ理論の出自がゲーム理論であることがわかる。)
_____
- 主に労働市場とマクロ経済の間に存在する相互作用を研究するため開発したサーチ・マッチング理論における貢献が著名である。彼は、失業から雇用に至るフローにおけるマッチング関数理論の概念を開発および支援その推定に関する実証的研究の先駆者と云える。
- 最も影響力のある論文は、1994年にレビュー・オフ・エコノミック・スタディズで発表された「雇用創出および雇用喪失における失業理論」である[5]。この論文はその前の20年間においてデール・モーテンセンとピサリデスの両著者による個々の貢献に基づいて構築されていた。この論文に起因したモーテンセン=ピサリデスモデルは、現代マクロ経済学において非常に強い影響を与えてきた。それはなんらかの変動かまたは拡大をもたらし、今日において世界中の至る所で経済学における卒業カリキュラムの核の一部として採用されている。
- ピサリデスの著書「均衡的失業理論」Equilibrium Unemployment Theory 2000 はマクロ経済学において失業理論における文献として幅広く参照されている。
- デール・モーテンセンとピサリデスによる共同作業において、内因的な雇用創出および雇用喪失における分析の結果、改定されている。
- 近年は発展と構造変化に関する研究を行っている。
http://www.amazon.com/Equilibrium-Unemployment-Theory-2nd-Edition/dp/0262161877
http://www.amazon.co.jp/Equilibrium-Unemployment-Theory-Press/dp/0262161877/
http://www.gbv.de/dms/ilmenau/toc/30113880X.PDF
Equilibrium Unemployment Theory second edition
Christopher A. Pissarides
The MIT Press Cambridge,Massachusetts London, England
Contents
Preface
Preface to the First Edition
I FOUNDATIONS
1 The Labor Market
2 Endogenous Job Destruction
3 Long-Run Equilibrium and Balanced Growth
II FURTHER ANALYSIS OF THE LABOR MARKET
4 Labor Turnover and On-the-Job Search
5 Search Intensity and Job Advertising
6 Stochastic Job Matchings
7 Labor Force Participation and Hours of Work
III CONSTRAINED EFFICIENCY AND THE ROLE OF POLICY
8 Efficiency
9 The Role of Policy
Bibliography
J は仕事が充足されている価値です。実質利子率 r が大きくなれば rJ が大きくなりますが、それは J がより多く割り引かれるということです。
この(1)式と欠員状態の価値を表わす式(これは省略)から、次の式が導出されます。
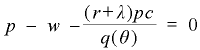
(2)
いわゆるベバリッジ曲線(失業率と欠員率との関係)は、次の式で表わされます。
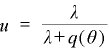
λは単位時間に仕事が破壊される割合(確率)です。q は m/v,m はマッチング関数(u,v の投入でどれだけの労働者と仕事の組み合わせができるかを表わしたもの)、v は欠員率なので q=m/v は、欠員の仕事が補充される割合(確率)を表わしています。θ= v/u (v:欠員率、u = 失業率) です。
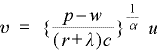
(4)
となります。これは(u,v) の空間で原点を通る直線です。
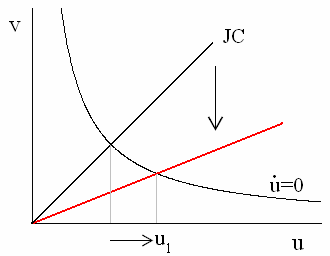
そこで、実質利子率 r が増加すると、(4)式の傾きが小さくなるので、か job creation curve が下にシフトします。
その理由は、(1)式から仕事の価値が大きく割り引かれることになるため、企業は仕事をつくらなくなるからです。job creation curve が下にシフトすれば、上の図のように、均衡失業率は増加します。
これは現実のデータに合っているように思われます。以下はクルーグマンがブログ("Moochers, Grifters, and the Beveridge Curve," 拙訳はこちら)で引用していたもの。
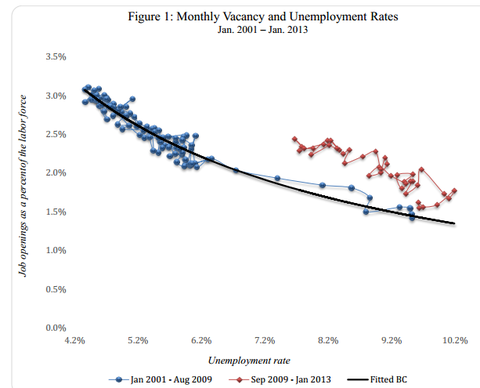
2009年8月以前のデータは青い点で示されています。それ以後のデータは赤い点で示されています。均衡失業率は右のほうにシフトしています。
しかし、このデータでは、ベバリッジ曲線自体が右上にシフトしていることも気になります。
サーチモデルから想定される、ベバリッジ曲線を右上にシフトさせる要因は、仕事の破壊率λの上昇です。(3)式のλが増加すれば、u は大きくなります。したがってベバリッジ曲線を外にシフトさせます。
前のケースのように job creation curve が下にシフトし、ベバリッジ曲線が外にシフトすれば、下の図のように均衡失業率はさらに大きくなります。
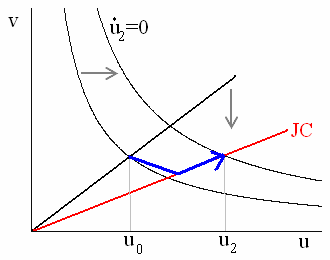
このモデルでλは外生的に与えられるパラメーターで、技術進歩のような、長期間において仕事と労働者とを切り離す割合が想定されています(技術進歩が進めば、労働者1人当たりの生産性が増すので、労働者と仕事を切り離す[=破壊する]確率は減る。つまりλが低下する)、しかし、現在、技術進歩のペースが落ちて、λが増加していると想定するのは難しいです。
ベバリッジ曲線が右上にシフトしていることは、欠員率 v が増加しているということです。サーチモデルでは、労働者は直接企業に雇われるわけではありません。企業は、労働者を雇う前に、仕事を欠員状態にして準備しておかなければなりません(例えば車や機械やコンピューターを用意していおく)。失業が多くなれば、労働者がやってくる確率が高くなるので、企業は仕事を充足させるつもりなら欠員の仕事を増やします。
上の図のデータのように、失業率が高いのに、欠員率も高いのは、企業は労働者を雇用しようと思って仕事を開いているにもかかわらず、雇用が進んでいないということを表わしています。
ピサリデスは、ベバリッジ曲線を表わす(3)式に代わるものとして、次のベバリッジ曲線の式を想定しています。
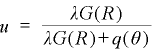
ここで R は、企業が労働者をとどめておきたいと思う最低レベルの生産性を表わしていて、G(R) は、労働者の生産性が R以下になる確率です。このモデルにしたがえば、ベバリッジ曲線が外へシフトしたのは、企業が、労働者に求める生産性を引き上げた( G(R) が増加した)、ということになります。
クルーグマンは4月21日のコラム(「失業の罠」、"Jobless Trap," 拙訳はこちら)で、長期間失業している労働者が労働者として「劣等」と認識される傾向が増えた(それは長期間する失業する失業者の割合が増えていることにもつながっている)、と言っています。クルーグマンはベバリッジ曲線に言及しているブログでは、これをベバリッジ曲線の外へのシフトの原因として挙げていませんが、ベバリッジ曲線が外にシフトしているのは、これが原因かもしれません(企業が労働者に対する「生産性のハードル」を上げた)。
(2) ローマー、『上級マクロ経済学』のサーチとマッチングのモデル(ピサリデスのモデルをもとにしたもの)
(9.81)
_____
スティグリッツは近著で人がどのような過程で職を得るかをモデル化したサーチ理論を絶賛
している(「過去数十年で経済理論に生じた重要な進歩のひとつは..."サーチ理論"だ」『新し
い教科書』2016邦訳245頁)。その「不完全な労働市場」観(さらに離散的なそれ)はスティ
グリッツのいう情報の非対称性を前提にしたものだ。
失業率の決定:
求人率(V)
|
| o
| /
| o / 有効求人倍率
| /
| o /
|____/
| /o
| / | o
| / | o o ベバリッジ曲線、UV曲線
|/___|___________
欠員率、失業率(U)
(政府による失業者に対する教育訓練が功を奏して、仕事を失った失業者がよりスムーズに
別の仕事に就くことが出来るようになれば、UV曲線、ベバリッジ曲(Beveridge Curve:
定常状態における失業率Uと求人率Vの関係を表したもの)は内側にシフトする。
『齋藤他マクロ』#16,568頁参照。)
参照:
労働市場サーチ理論 今井亮一
http://www.jil.go.jp/institute/zassi/backnumber/2012/04/pdf/016-019.pdf
提示賃金の分布と留保賃金(例):
確率(合計は1)
: 留保賃金
0.25| 拒否←|→受諾 _
| | |/|
0.20| | _ |/|
| _ | |/| |/|
0.15| |/| | |/| |/|
| _ |/| | |/| |/|
0.10| |/| |/| | |/| |/|
| |/| |/| | |/| |/|
0.05| |/| |/| | |/| |/|
|_|/|___|/|_|_|/|___|/|___
0 17 18 19 20 万円(提示賃金)
(齋藤他565頁参照)
http://ejje.weblio.jp/content/beveridge
日本語WordNet(英和)での「beveridge」の意味
英国の経済学者(インド生まれ)で、社会保険についてのレポートが英国の福祉志向国家が基づく社会立法の大部分に基礎を提供した(1879年−1963年)
(British economist (born in India) whose report on social insurance provided the basis for most of the social legislation on which the welfare state in the United Kingdom is based (1879-1963))
ベバリッジ曲線
https://upo-net.ouj.ac.jp/tokei/xml/kw2_13034.xml
ベバリッジ曲線 Beveridge curve
横軸に失業率,縦軸に欠員率をとり,失業率と欠員率の関係を描いた曲線である.失業率と欠員率とは逆相関的な関係にあり,原点に対して凸型の曲線となる.失業(Unemployment)と欠員(Vacancy)の頭文字をとってUV曲線ともいう.英国の経済学者W.H. Beveridge(1879-1963)のアイディアによる分析手法である.失業率は,たとえ労働供給を上回る労働需要があっても,ゼロにはならない.これは,求人と求職の結合にかかる時間や,求職者の技能や生活上の条件が適合しない等のために失業が発生するからである.もし労働市場における迅速な情報伝達や十分な職業訓練が実施されているなどの状況にあれば,失業率や欠員率はより低くなり,この曲線は原点に向かってシフトすることになる.
ウィリアム・ベヴァリッジ - Wikipedia
https://ja.wikipedia.org/wiki/%E3%82%A6%E3%82%A3%E3%83%AA%E3%82%A2%E3%83%A0
ウィリアム・ヘンリー・ベヴァリッジ(William Henry Beveridge、1879年3月5日 - 1963年3月16日)は、イギリスの経済学者、政治家。1942年に発表された「社会保険と関連サービス」(ベヴァリッジ報告として知られる)と題された報告書は、第二次世界大戦後のイギリスだけでなく、日本を含む先進諸国の社会保障制度の構築に多大な影響を与えた。
国家公務員生活の後、ロンドン・スクール・オブ・エコノミクス(LSE)の学部長、オックスフォード大学ユニバーシティ・カレッジの学寮長などを務めた。政府の委員会に多数関わり「ゆりかごから墓場まで」を目標としたイギリスの社会保障や雇用施策の充実に貢献。思想的・学問的にはフェビアン協会のウェッブ夫妻、経済学者ジョン・メイナード・ケインズから多大な影響を受けた。
1942年11月、政府刊行物として発刊された報告書『社会保険および関連サービス』をベヴァリッジ報告と呼ぶ。社会保障の大前提として「完全雇用の維持」「所得制限なしの児童手当」「包括的な保健サービスの提供」の3つを挙げ、社会保障制度の原則として「均一拠出・均一給付の原則」を提示した。
1944年より補欠選挙に出馬して自由党議員となり、議会の場においてもベヴァリッジ報告に基づく社会改革の実施を主張した。第二次世界大戦後のアトリー労働党内閣においてこの構想は実現へとむかい、「包括的な保健サービス」としてNHS(国民保健サービス)という、患者負担無料(当時)・税方式の医療保障制度が生まれた。
ベヴァリッジ曲線
失業者(失業率)と企業の人員不足(欠員率)の間に負の関係を示した理論[1]。性、年齢、職業、学歴、熟練の度合い、地域、産業の違いにより労働者の適正がさまざまであることを重視したベヴァリッジ曲線を分析することで求職・求人がマッチするための情報源となる[2]。
脚注
^ 日本経済新聞社編 『やさしい経済学』 日本経済新聞社〈日経ビジネス人文庫〉、2001年、215頁。
^ 日本経済新聞社編 『やさしい経済学』 日本経済新聞社〈日経ビジネス人文庫〉、2001年、216頁。
参考文献 編集
Jose Harris著 (柏野健三訳) 『ウィリアム ベヴァリッジ その生涯 (上 中 下)』ふくろう出版
http://www.amazon.co.jp/dp/4861861438/
Lord Beveridge著 (柏野健三訳) 英国思想・ベヴァリッジ研究所研究叢書No.1
http://www.amazon.co.jp/dp/4589036320/
ベヴァリッジの経済思想―ケインズたちとの交流 単行本 – 2007/3 小峯 敦 (著)
http://www.amazon.co.jp/dp/4812207142/
『英国の知力 ロンドン大学ロンドン・スクール・オブ・エコノミックス(LSE)激動と躍進の18年 (1919〜1937)』英国思想・ベヴァリッジ研究所2010年6月
http://ci.nii.ac.jp/ncid/BB14448172
________________
8-6(78)【2003.11】「消費者行動のモデル化に関する一考察 情報処理 ...
サーチ ・ マッチング理論に基づく国際貿易と 失業率の ... - 青山学院図書館
にとって背任が純粋に個人的利益となるのは
の積を上回るときである。
れる収入を上回る額」で、これを特に
にとって価値あるものにし、解雇を避けるべき努力につながる。
だから、そこで「失業」が生じることになる。
しても、クビになった時から再就職の間の収入減が生じるのはやむ
を得ない。
部雇用機会と比べてより高い賃金を設定できるように「失業が創出」
されるのだ。
損失になるが、このモデルを特にシャピロ=スティグリッツのモデ
ルと言う。
会が乏しく、新卒者が企業にほぼ終身的に雇用されると言う社会状
況が、そういう背任を防止するための大きな要因になっていた。
失う便益がドでかかったために、日本人は安めの賃金で労働するこ
とに不満を持っても、勤勉に働いたということである。
解でも構わない(拙「インセンティブで考える」参照)が、かなり
転職が定着した日本においてどのような賃金体系が妥当であるかは、
かなり難しい問題だといえる。
酬βということになるのだろうが、、、
前回の補足(20)で、ローマー、『上級マクロ経済学』の中の シャピロ=スティグリッツ モデルの説明(9章4節)を取り上げましたが、シャピロ=スティグリッツの論文自体の説明のほうがすっきりしています。
Carl Shapiro and Joseph E. Stiglitz,
"Equilibrium Unemployment as a Worker Descipline Device" (1984)
c*
|
| de/dt=0
y| o
| o
| o o @ o dc/dt=0
| o o A
| o o
|o @ o o
| o B
|________________e
0 1
cは生産に要する努力。eは雇用率。均衡点はAB二つある。
Aggregate Demand Management in Search Equilibrium. Peter A. Diamond. Massachusetts Institute of Technology. Equilibrium is analyzed for a simple barter model with identical ... [Journal of Political Economy, 1982, vol. 90, no. 5]
http://homepage.ntu.edu.tw/~yitingli/file/macro%20and%20money/Aggregate%20Demand%20Management%20in%20Search%20Equilibrium.pdf
__________
動学的一般均衡のマクロ経済学―有効需要と貨幣の理論 単行本 – 2005/9/1
大瀧 雅之 (著)
第1章でサーチ理論解説