NAMs出版プロジェクト: ミルグロム『組織の経済学』1997*
http://nam-students.blogspot.jp/2016/10/blog-post_10.html
http://nam-students.blogspot.jp/2016/10/blog-post_10.html
NAMs出版プロジェクト: ベン卜・ホルムストローム 2016ノーベル経済学賞
http://nam-students.blogspot.jp/2016/10/2016_32.html
http://nam-students.blogspot.jp/2016/10/2016_32.html
NAMs出版プロジェクト: オリバー・ハート 2016ノーベル経済学賞
http://nam-students.blogspot.jp/2016/10/2016_39.html
http://nam-students.blogspot.jp/2016/10/2016_39.html
NAMs出版プロジェクト: ジャン・ティロール2014年ノーベル経済学賞
http://nam-students.blogspot.jp/2016/10/2014.html
http://nam-students.blogspot.jp/2016/10/2014.html
柳川 範之
https://nam-students.blogspot.com/2019/01/kindle.html@
同じ柳川姓でもこちらを先に読んだ方がいいかも
契約理論を紹介している数少ない入門書
2008年版でも問題ない
同じ柳川姓でもこちらを先に読んだ方がいいかも
契約理論を紹介している数少ない入門書
2008年版でも問題ない
ミクロ経済学・入門--ビジネスと政策を読みとく 新版 (有斐閣アルマ) 単行本(ソフトカバー)– 2015/3/23
ミクロ経済学・入門 ービジネスと政策を読みとく 新版 (有斐閣アルマ) 2015/3/23 柳川 隆 , 町野 和夫 , 吉野 一郎
改訂新版試作:
経済学説の系譜と論点: ○ ○ ○
19世紀 20世紀 21世紀
リカード 分析的マルクス主義
投下労働価値説━労働価値説・恐慌論━━┳正統派 数理的マルクス主義
┃┃マルクス(学派)┗━━┓ ┗宇野派 森嶋通夫 A
┃┃ ┗━━カレツキ━┓┃ ┗━日本人経済学者 生産者費用
┃┗━━━━━スラッファ┃┃ 宇沢弘文 マルクス
┃ ┃┣━━━━━━━━━━レギュラシオン学派
┃┏━━━━━━━━━━┛┃ ______________________
┃┃ドイツ歴史学派━━━━制度学派 新制度学派
┃┃エンゲル シュモラー ヴェブレン コース ミルグロム
┃┃ ウェーバー ゾンバルト
┃┗━━━━━━━━━━━━━┓ D
┣プルードン━ゲゼル ┃ 岩村充 プルードン
┃ ┃ 生産者効用
┃ ┃ ____________________
┃ リンダール┃レーン=メイドナー 岩井克人
┃(北欧)ヴィクセル┳┛ ┃ 清滝信宏
┃ ケインズ ┃ ミンスキー スティグリッツ
┃ ケインズ学派┻ポスト・ケインジアン━ニュー・ケインジアン
17世紀 ┃ ┃ハロッド カルドア ロビンソン ┃ マンキュー
ペティ ┃ ケンブリッジ学派 ┃クルーグマン
┃ ┃ ┗━━━━━━━━┓サミュエルソン┏━┛
┗古典派┫ レオンチェフ ┣新古典派総合 ┣━━シムズ
A・スミス┣J.S.ミル ┏━━━━━━━━┛トービン ┗━┓
18世紀 ┃ マーシャル 部分均衡 奥野正寛┃
┃ ┃ピグー ルイス ┃ピケティ
┃ ┣━ヒックス IS・LM マンデル ┃ B
シスモンディ ┃ ┃ 消費者費用
マルサス ┃ラムゼー 外生的 成長理論 ソロー━┫ マルサス
支配労働価値説┓ ┃ ________┃ _______┃_______
┃ ┏┛ノイマン 内生的━┛ OLG ┃ゲーム
┗新古典派経済学 シュンペーター ローマー┃ 理論*
ワルラス 一般均衡 AKモデル┃ C
テュルゴー クールノー┃パレート シカゴ学派 バロー ┃ ワルラス
コンディヤック 主流派┃ クズネッツ フリードマン ルーカス ┃ 消費者効用
ケネー ┃ ┏マネタリズム━合理的期待学派┫
┃ ┃ サージェント┃
(貨幣中立説) フィッシャー┃RBC(リアル・ビジネス・サイクル)モデル
機械的貨幣数量説━━━┳貨幣数量説┛ 外生的 プレスコット
ヒューム ┃ ハイエク キドランド
連続的影響説 エッジワース ドラッカー ┃
シーニョア ┃オーストリア学派 内生的 ┏━━━┛
平均効用 限界効用 メンガー バヴェルク ┗DSGE
セイ ジェボンズ 転形論争
消費者 生産者
四元的 費用 B A
価値論 効用 C D
瀧澤弘和『現代経済学』より[上下逆にして改変]:
図2-4 ゲーム理論の影響を受けた諸分野とノーベル賞
1988 モーリス・アレ 市場と資源の効率的利用に関する理論
1991 ロナルド・コース 取引費用経済学
ゲーム理論_______________________________
1994 人間行動・制度 I I
ハーサニ/ナッシュ/ゼルテン 行動ゲーム理論 I
\ 実験ゲーム理論 I
\インセンティブ・制度設計 I I
\ I I
/\___情報の非対称性 I I
/ \ 1996マーリーズ/ヴィックリー I I
/ \ 2001アカロフ/スペンス/ I I
/ \ スティグリッツ I I I
/ \ I 行動/実験経済学 I
対立と協力 \ I 2002 I
2005 /\ I カーネマン/スミスI
オーマン/シェリング / \ I I I
/ \ I I I
マーケット・デザイン メカニズム・デザイン I I I
/ \ 2007 I I経済ガバナンスの理論
/ \ ハーヴィッツ/ I I 2009
サーチ理論 \ マスキン/ I I オストロム/
2010 \マイヤーソン I I ウィリアムソン
ダイアモンド/ \ \ I I
モーテンセン/ピサリデス \ \ I I
マッチング理論 \ \ I I
2012 オークション理論 契約理論 I
ロス/シャープレイ 2014 I
ティロール I
2016 行動経済学 ナッジ理論
ハート/ホルムストローム 2017
リチャード・セイラー
*ミルグロムはノーベル賞未受賞
岡田新版入門192頁参照
https://ja.wikipedia.org/wiki/%E3%83%97%E3%83%AA%E3%83%B3%E3%82%B7%E3%83%91% E3%83%AB%EF%BC%9D%E3%82%A8%E3%83%BC%E3%82%B8%E3% 82%A7%E3%83%B3%E3%83%88%E7%90%86%E8%AB%96
図2-4 ゲーム理論の影響を受けた諸分野とノーベル賞
1988 モーリス・アレ 市場と資源の効率的利用に関する理論
1991 ロナルド・コース 取引費用経済学
ゲーム理論_______________________________
1994 人間行動・制度 I I
ハーサニ/ナッシュ/ゼルテン 行動ゲーム理論 I
\ 実験ゲーム理論 I
\インセンティブ・制度設計 I I
\ I I
/\___情報の非対称性 I I
/ \ 1996マーリーズ/ヴィックリー I I
/ \ 2001アカロフ/スペンス/ I I
/ \ スティグリッツ I I I
/ \ I 行動/実験経済学 I
対立と協力 \ I 2002 I
2005 /\ I カーネマン/スミスI
オーマン/シェリング / \ I I I
/ \ I I I
マーケット・デザイン メカニズム・デザイン I I I
/ \ 2007 I I経済ガバナンスの理論
/ \ ハーヴィッツ/ I I 2009
サーチ理論 \ マスキン/ I I オストロム/
2010 \マイヤーソン I I ウィリアムソン
ダイアモンド/ \ \ I I
モーテンセン/ピサリデス \ \ I I
マッチング理論 \ \ I I
2012 オークション理論 契約理論 I
ロス/シャープレイ 2014 I
ティロール I
2016 行動経済学 ナッジ理論
ハート/ホルムストローム 2017
リチャード・セイラー
*ミルグロムはノーベル賞未受賞
岡田新版入門192頁参照
プリンシパル=エージェント理論 - Wikipedia 依頼人、代理人
プリンシパル=エージェント関係(-かんけい、principal-agent relationship)とは、行為主体Aが、自らの利益のための労務の ...
ボーナスb
|
|
| d
|\経営者にとっての
| \最適点の
| a\集まり
|_⬆︎_\__________
| |\↗︎c
| | \経営者の無差別曲線(左下ほど効用が高い)
|___|__\_______
0 固定賃金w
|
|
| d
|\経営者にとっての
| \最適点の
| a\集まり
|_⬆︎_\__________
| |\↗︎c
| | \経営者の無差別曲線(左下ほど効用が高い)
|___|__\_______
0 固定賃金w
aインセンティブ両立条件 c参加条件 dインセンティブ両立条件と参加条件を満たす(w,b)の集合
(新用語・難解用語)プリンシパル・エージェント問題 | 上場会社役員ガバナンスフ ...
自らの利益のための労務の実施を他の行為主体に委任する場合、依頼人を「 プリンシパル」、代理人を「エージェント」と呼ぶ。
プリンシパル=エージェント理論とは - Weblio辞書
プリンシパル=エージェント関係(-かんけい、principal-agent relationship)とは、行為主体Aが、自らの利益のための労務の ...
《一九八〇年代後半には、経済学者のベン卜・ホルムストロームとポール・ミルグロム
により、もう一つの重要な研究結果が示された。両氏は数々の仮説に基づく極めて理論的
な論文において、通常は売上高にかかわらず歩合をー定に保つのが、営業担当者の報酬制
度として最適であると結論づけた。さまざまな種類のボーナスを設けたり、一定期間内に
目標を達成した人に以後は別の報酬体系を適用したりするなど、仕組みを複雑にしすぎる
と、担当者たちはそれにうまく乗じる方法を見つけ出すだろう、というのだ。
…
ホルムストロームとミルグロムが提案したようなシンプル極まりない報酬体系は、訴求
力がありそうに見えるが(理由のーつとして、運用しやすくコストもかさまない)、実際のと
ころ、多くの企業はもっと複雑な仕組みを選ぶ。「営業担当者はそれぞれ個性があり、モ
チべーションやニーズが異なるため、いくつもの要素から成る報酬体系のほうが幅広い層
にアピールするだろう」と考えるのだ。その理屈でいえば、個々の担当者から最高の成果
を引き出すには、個別に報酬体系を決めるべきだということになる。…》
(「営業を本気にさせる報酬制度とは」ダグ J.チュン ハーバード・ビジネス・スクール 助教授
DIAMONDハーバード・ビジネス・レビュー 2015年8/01号)
により、もう一つの重要な研究結果が示された。両氏は数々の仮説に基づく極めて理論的
な論文において、通常は売上高にかかわらず歩合をー定に保つのが、営業担当者の報酬制
度として最適であると結論づけた。さまざまな種類のボーナスを設けたり、一定期間内に
目標を達成した人に以後は別の報酬体系を適用したりするなど、仕組みを複雑にしすぎる
と、担当者たちはそれにうまく乗じる方法を見つけ出すだろう、というのだ。
…
ホルムストロームとミルグロムが提案したようなシンプル極まりない報酬体系は、訴求
力がありそうに見えるが(理由のーつとして、運用しやすくコストもかさまない)、実際のと
ころ、多くの企業はもっと複雑な仕組みを選ぶ。「営業担当者はそれぞれ個性があり、モ
チべーションやニーズが異なるため、いくつもの要素から成る報酬体系のほうが幅広い層
にアピールするだろう」と考えるのだ。その理屈でいえば、個々の担当者から最高の成果
を引き出すには、個別に報酬体系を決めるべきだということになる。…》
(「営業を本気にさせる報酬制度とは」ダグ J.チュン ハーバード・ビジネス・スクール 助教授
DIAMONDハーバード・ビジネス・レビュー 2015年8/01号)
新しい理論の特徴
新しい契約理論の特徴のひとつは,経済問題を単なる市場取引と考えるのではなく,今まで経済学が(暗黙のうちに)所与とし,あまり分析の対象としてこなかった制度や慣習,法律といったものが経済に与える影響を分析していることです.その結果,ミクロ経済学の分析対象は大きく広がり,今まで以上にさまざまな興味深い分析ができるようになってきました.
これまでの契約理論(完備契約理論)は,上で述べたように,モラルハザードや逆選択といった情報の非対称性から生じる問題を主に扱ってきました.そして,どのような契約を書けば,情報の非対称性から生じる損失を小さくできるか,というのが分析の中心でした.たとえば労働契約を考えた場合,労働者の努力水準が分からないならば,努力水準のシグナルである生産量に依存した賃金契約を書くことによって,努力水準を間接的にコントロールしようとしました.そして,生産量に依存した契約の中でどれが一番望ましいか,という形で最適な契約の問題が議論されてきました. ★ 1
しかし,現実にはこれまでの契約理論が想定しているようには契約は書かれていません.理論が要請する最適契約というのは複雑になっている場合が多いのですが,現実の契約はそれほど複雑ではありません.また,契約を書くこと自体,大きなコストがかかり,契約そのものが書かれていない場合も多いのです.新しい契約理論(不完備契約理論)はこの事実を踏まえ,契約が書かれていない,あるいは複雑な契約が書かれていない状況を出発点とします.そして契約がうまく書かれていない場合に,制度や法律,組織といったものが,どのように契約を補完しているのか,そしてどのように補完するべきか,というのが基本的テーマとなっています. ★ 2
〔注〕
★ 1 この点に関心のある読者はたとえば, Hart and Holmström( 1987)を参照してください.
★ 2 このような主張は,かなり以前から議論になってはいました.たとえば, Williamson( 1985)や, Klein et al.( 1978)を参照してください.
Williamson, O. (1985), The Economic Institutions of Capitalism, New York: Free Press.
Klein, B., R. Crawford and A. Alchian (1978), "Vertical Integration, Appropriable Rents and the Competitive Contracting Process," Journal of Law and Economics, 21: 297-326.
(3) 伝統的契約理論
情報の経済学と重複する部分も多いのですが,本書ではほとんど説明することができなかった伝統的な契約理論については, Salanie, B. (1997), The Economics of Contracts, MIT Press. Hart, O., and B. Holmström (1987), "The Theory of Contracts," in T. Bewley( ed.), Advances in Economic Theory, Cambridge University Press, pp. 71-155.といった文献が挙げられます.ともに英文ですが,前者は初学者向けのテキストで,後者は少し前に書かれたサーベイ論文です.
また,組織の問題について具体例を豊富に交えたテキストとしては, Milgrom, P., and J. Roberts (1992), Economics, Organization and Management, Englewood Cliffs.(奥野他訳( 1997)『組織の経済学』 NTT出版)があります.
ところで,本書は不完備契約理論に焦点を絞って解説していますが,参考文献には伝統的契約理論の文献もかなり挙げておきましたので,参考にしてください.その中でも基本的な論文としては以下のようなものが挙げられます.
モラルハザードの問題を扱ったプリンシパル-エージェントモデルは, Holmström (1979) (1982), Shavell (1979), Lazear and Rosen (1981)といった論文が古典的論文です. Holmström (1982)はチーム生産の問題を, Lazear and Rosen (1981)はトーナメントの問題を扱っています.
発展モデルとしては, Holmström and Milgrom (1990)はエージェントが複数の作業をする問題を扱っており, Hermalin and Katz (1991)は再交渉の問題を扱っています. Holmström (1999)は昇進などダイナミックな側面を扱っています.
逆選択といった情報の非対称性の問題については, Fudenberg and Tirole (1991)に詳しい解説があります. Baron and Myerson (1982), Maskin and Riley (1984), Laffont and Tirole (1986)といった論文が古典的な基本論文であり, Maskin and Tirole (1990) (1992), Dewatripont (1989), Tirole (1992), Bernheim and Whinston (1986)といった論文が著名な発展論文です. Tirole (1992)は組織内の共謀の可能性を考慮しており, Bernheim and Whinston (1986)は複数のプリンシパルが同じエージェントを使う問題を扱っているという特徴があります.
Holmström, B. (1999), "Managerial Incentive Problems ─ ─ A Dynamic Perspective," Review of Economic Studies, 66: 169-82.
参考の参考:
山本論考
人的資源管理における非金銭的誘因の効果 (Adobe PDF)
豊福佐藤論考
〈日本知財学会誌〉Vol.5 No.2―2008 : 72―87
不完備契約理論に関する基本文献
今のところ不完備契約理論についての解説書は,英文の Hart, O. (1995), Firms, Contracts, and Financial Structure, Oxford University Press.がほぼ唯一のものです.この本はテキストとして書かれたものではないので,説明がやや専門的になっている部分がありますが,本書で扱った内容の多くをカバーしています.
組織の問題を議論してきた古典的論文としては, Coase (1937), Alchian and Demsetz (1972), Klein et al. (1978), Williamson (1985)といった論文があります.サーベイ論文としては Holmström and Tirole (1989)が詳しく解説しています.
第 1章から第 4章までで説明している不完備契約アプローチを明確に展開したのは, Grossman and Hart (1986), Hart and Moore (1988) (1990)といった論文です.
第 5章で説明しているような形式的権限と実質的権限の違いは, Aghion and Tirole (1997)によって明確にされました.
その他の論文では, Holmström and Milgrom (1994), Stole and Zwiebel (1996), Rajan and Zingales (1998)といった論文が,本書で扱わなかった側面から組織の問題を検討しています.
第 6章で検討した法律との関係については, Edlin and Reichelstein (1996)が検討しています.(ただしこの論文についての解説は第 13章で行っています.)邦文文献としては,三輪・神田・柳川 (1998)があります.
第 7章,第 8章で検討した公的組織の問題については, Schmidt (1996), Shleifer and Vishny (1994), Qian and Roland (1997),Hart et al. (1997)といった論文があります.
第 9章,第 10章および第 14章で検討した金融契約への応用は多くの優れた論文がありますが, Aghion and Bolton (1992), Hart and Moore (1994) (1998), Dewatripont and Tirole (1994 a)といった論文が基本文献です.本書で扱えなかった多数の債権者がいるケースは, Bolton and Scharfstein (1996)で検討されています.また銀行規制については,Dewatripont and Triole (1994 b),(北村・渡辺訳)を参考にしています.
第 12章で検討したマクロへの応用はまだ少ないのですが, Kiyotaki and Moore (1998), Holmström and Tirole (1997)といった論文が出てきています.
第 13章で議論した不完備契約の理論的基礎付けについては,最近になって多くの論文が出てきていますが,ここでは Tirole (1999), Segal (1999), Maskin and Tirole (1999 a) (1999 b), Hart and Moore (1999), Che and Hausch (1999), Segal and Whinston (1998)を挙げておきます.
Edlin, A. S., and S. Reichelstein (1996), "Holdups, Standard Breach Remedies, and Optimal Investment," American Economic Review, 86: 478-501.
三輪芳朗・神田秀樹・柳川範之編( 1998)『会社法の経済学』東京大学出版会.
Dewatripont, M. and J. Triole (1994 b), The Prudential Regulation of Banks, MIT Press.(北村行伸・渡辺努訳( 1996)『銀行規制の新潮流』東洋経済新報社)
Tirole, J. (1999), "Incomplete Contracts: Where Do We Stand?" Econometrica, 67: 741-81.
Maskin, E., and J. Tirole (1999 a), "Unforeseen Contingencies and Incomplete Contracts," Review of Economic Studies, 66: 83-114.
Hart, O., and J. Moore (1999), "Foundations of Incomplete Contracts," Review of Economic Studies, 66: 115-38.
Holmström, B., and P. Milgrom (1987), "Aggregation and Linearity in the Provision of Intertemporal Incentives," Econometrica, 55: 303-28.
Holmström, B., and P. Milgrom (1990), "Multi-Task Principal Agent Analyses," Journal of Law, Economics and Organization, Vol. 7. Sp., pp. 24-52.
Holmström, B., and P. Milgrom (1994), "The Firm as an Incentive System," American Economic Review, 84( 4): 972-91.
Hart and Holmström( 1987) の収録された論集 2013年電子化
Advances in Economic Theory Fifth World Congress Advances in Economic Theory Get access Cited by 3
______
はじめに
序章 契約理論の新展開
第 1章 不完備契約の考え方
1‐ 1 完備契約の世界:コースの定理
1‐ 2 不完備契約のケース
第 2章 不完備契約理論の基礎
2‐ 1 単純な理論モデル
2‐ 2 複雑なモデル
第 3章 企業の境界と所有権の配分
3‐ 1 企業の境界
3‐ 2 モデル分析
3‐ 3 所有権の配分
第 4章 権限配分への応用 4‐ 1 組織内の権限配分
4‐ 2 簡単なモデル 4‐ 3 仮定のもつ意味
第 5章 形式的権限と実質的権限
5‐ 1 形式的権限からの乖離
5‐ 2 モデル分析
5‐ 3 知識レベルが外生的な場合
5‐ 4 知識レベルが内生的な場合
第 6章 法律の役割
6‐ 1 会社法の規定
6‐ 2 法律の役割:完備契約の場合
6‐ 3 法律の役割:不完備契約の場合
6‐ 4 強行規定の必要性
第 7章 公的企業組織の問題
7‐ 1 公的企業の特徴
7‐ 2 ソフトな予算制約問題
7‐ 3 官僚組織の問題
第 8章 民営化の問題
8‐ 1 国営か民営か
8‐ 2 完備契約の場合の民営化
8‐ 3 国営と民営の違い
8‐ 4 モデル
8‐ 5 ソフトな予算制約問題との関連
第 9章 金融契約への応用
9‐ 1 不完備契約と金融取引
9‐ 2 ベンチャー企業の資金調達
第 10章 負債の役割
10‐ 1 負債と決定権限
10‐ 2 経営者のインセンティブとコーポレート・ガバナンス
第 11章 銀行規制問題への応用
11‐ 1 銀行規制の議論
11‐ 2 銀行経営者のインセンティブ
11‐ 3 自己資本比率規制
11‐ 4 自己資本比率規制とマクロショック
第 12章 マクロモデルへの応用
12‐ 1 マクロ経済への応用の可能性
12‐ 2 金利の内生化
12‐ 3 景気変動への影響
第 13章 不完備契約モデル:理論編
13‐ 1 不完備契約理論モデル
13‐ 2 不完備契約の基礎づけ
第 14章 金融契約モデル:理論編
14‐ 1 非効率的交渉
14‐ 2 インセンティブへの影響
文献案内
6-1
…不完備契約の世界では単純に契約だけでは効率性が達成されません.そのため,図 6‐ 1にあるように,契約と法律や制度,それから組織といったものがそれぞれ補完し合って総合的に,効率性の実現やインセンティブのために機能することになります.これが,法律が果たしている重要な役割のひとつです.
ただし,企業が決定する際には,法律や制度はすでに決まっている外生変数です.そのため,決められた法律を前提として,企業は最適な契約および組織形態を選択することになります。
(契約)
↗︎ ↖︎
(契約)→[効率性] ↙︎ 補完 ↘︎ →[効率性]
(法律)←→(組織)
14-2
u
|
|
|
|
| ̄-_ X=1
|X=0 ̄-_
^|______ ̄-_________
u| |  ̄-_ X=1
| |  ̄-_
| X=0 |  ̄-
| |
| |
| |
| |
|_______|_________y
y1
横軸に水平に書かれている直線は,事後的な効率性だけを考えた場合の最適な決定ルールを表しています.事後的な効率性だけを考えるのであれば, uだけを基準に判断すればよいため,水平になっています.したがって図の斜線の部分が,事後的な効率性と,事前の効率性とが乖離している,つまり意図的に事後的な非効率性をつくり出している部分ということになります.
しかし先にも述べたように, uは立証可能な変数ではないので,上で述べたような最適決定ルールを契約によって実行させることは困難です.そこで株式と社債という二つの金融商品を発行することによって,上の最適決定が行われるようにするのが,以下での課題です.
契約と組織の経済学 Kindle版
- フォーマット: Kindle版
- ファイルサイズ: 9881 KB
- 紙の本の長さ: 246 ページ
- 出版社: 東洋経済新報社 (2000/4/3)
ミクロ経済学の最新動向は価格メカニズムを中心とした分析から、契約、取引、組織に注目した分析に移っている。本書は、この最新テーマをやさしく解説。
【主な内容】
はじめに
序 章 契約理論の新展開
第1章 不完備契約の考え方
第2章 不完備契約理論の基礎
第3章 企業の境界と所有権の配分
第4章 権限配分への応用
第5章 形式的権限と実質的権限
第6章 法律の役割
第7章 公的企業組織の問題
第8章 民営化の問題
第9章 金融契約への応用
第10章 負債の役割
第11章 銀行規制問題への応用
第12章 マクロモデルへの応用
第13章 不完備契約モデル:理論編
第14章 金融契約モデル:理論編
文献案内
【主な内容】
はじめに
序 章 契約理論の新展開
第1章 不完備契約の考え方
第2章 不完備契約理論の基礎
第3章 企業の境界と所有権の配分
第4章 権限配分への応用
第5章 形式的権限と実質的権限
第6章 法律の役割
第7章 公的企業組織の問題
第8章 民営化の問題
第9章 金融契約への応用
第10章 負債の役割
第11章 銀行規制問題への応用
第12章 マクロモデルへの応用
第13章 不完備契約モデル:理論編
第14章 金融契約モデル:理論編
文献案内
内容(「BOOK」データベースより)
最先端のテーマを、数式を用いずにやさしく解説。
______
豊福佐藤論考
〈日本知財学会誌〉Vol.5 No.2―2008 : 72―87



_____
不完備契約理論
サーベイ論文としては Holmström and Tirole (1989)が詳しく解説しています.
第 12章で検討したマクロへの応用はまだ少ないのですが, Kiyotaki and Moore (1998), Holmström and Tirole (1997)といった論文が出てきています.
by柳川
Holmström, B., and J. Tirole
Holmström, B., and J. Tirole (1989), "The Theory of the Firm," in The Handbook of Industridl Organization, R. Schmalensee and R. Willig (eds.), Amsterdam: North Holland.
Holmström, B., and J. Tirole (1997), "Financial Intermediation, Loanable Funds, and the Real Sector," Quarterly Journal of Economics, 52, 663-692.
____
------------------------------------------------------------
インセンティブ契約の実現可能性
------------------------------------------------------------
----------
■線型報酬関数を支える論理
----------
従業員に与えるインセンティブ報酬のモデルは eを努力水準、
xを需要水準(確率変数)、yをその産業全体に対する需要水準と
したとき
w(賃金)=α(基本給)+β・(e+x+γy)
であった。
もちろんこのような線型の式で表されるような報酬体系以外にも、
世の中には様々な形のインセンティブ契約が存在する。
たとえばセールスマンが一定以上の業績を挙げたときのみに支払
われる「成功報酬」である。
商品やサービスを売った分だけ歩合を与えるというやり方で、モ
ノを仕入れて売るだけの販社によくあるパターンである。
だがしかしこういう形式の契約には、大きな欠点がある。
それは
「最初につまづいて、その成功報酬をもらうための規準となる業績
に達しない見込みになるや否や、従業員のインセンティブが急激に
落ちる」
ということである。
与えられたノルマや達成水準に達しなければボーナス無し、とい
う条件下では、達成率30%も達成率99%も同じであるから、期
末に達成率が100%を越えなさそうだとわかった時点で従業員は
努力を止めて転職先を探し出し始めてしまう。
だからそういう契約ではなく、線型の歩合給の形でインセンティ
ブ契約を結ぶというのは、売り上げを伸ばすために一様なインセン
ティブを与えるために有効なのである。
線型の歩合給形式のインセンティブなら、期末に達成水準に達し
ないと分かった状態でも、次に一つ商品を売ったときに成功報酬を
受け取れるならセールスマンは商品を売ろうとするからである。
線型報酬関数に基づくインセンティブ契約は、そういうわけで従
業員に一様なインセンティブ・プレッシャーを与えることができ、
インセンティブ契約の最も良いモノの一つであると考えられる。
----------
■線型契約の下での総所得
----------
雇用主が中規模以上の企業の場合、従業員一人が担えるリスク負
担能力は、雇用主と比べて取るに足らないくらい小さい。
このため、インセンティブの問題を考えないとすれば、従業員の
給与に変動をもたらす全てのリスク発生源に対して保険を掛け、雇
用主が金銭的リスクを全部負担するのが最適であろう。
だがしかし、報酬中の全てのリスクを取り除いてしまうと、努力
水準を高めて利潤を増大させるインセンティブが、同時に従業員か
ら失われてしまう。
だから問題は(何度も書くが)リスク・シェアリングとインセン
ティブを与えバランスなのである。
さてここで、努力水準eと雇用主から与えられたインセンティブ
契約の規準となるパラメータα(固定給)、β(インセンティブ強
度)、γを考えてみる。
つまりベクトル(e、α、β、γ)によって、従業員の報酬が決
定されるようなインセンティブ契約を考えるわけである。
このとき従業員の確実同値額は、
「報酬の期待値」-「努力に要する費用」-「リスク・プレミアム」
となり、ゴチャゴチャ計算して簡素化すると、
α+βe-C(e)-(1/2)rβ^2・Var(x+γy)
となる。
そしてまた、同時に雇用主の確実同値額は、
「粗利潤の期待値」-「報酬支払い額の期待値」、つまり
P(e)-(α+βe)
である。
そういうわけで、従業員と雇用主の式を足しあわすと
「線型契約下における総所得」
が計算でき、それはつまり
P(e)-C(e)-(1/2)rβ^2・Var(x+γy)
ということになる。
----------
■努力インセンティブと、契約の実現可能性
----------
さて今、従業員の確実同値額は、
α+βe-C(e)-(1/2)rβ^2・Var(x+γy)
であった。
これはつまり従業員にとって収入が大きく変動すると困るから、
リスク・プレミアム分だけ安くていいから給料の基幹部分を固定給
にして、後はインセンティブ契約(つまり一部歩合給)で給与をも
らおうという仕組みである。
だからもし従業員に上手くインセンティブを与えて業績を伸ばそ
うと雇用主が考えるなら、従業員の努力水準eが、他のパラメータ
とどういう関係にあるか、確かめておかねばならない。
努力しても見返りがないなら、インセンティブ契約にはならない
から、βe-C(e)≧0は明らかであろう。がそれだけでは、適当な
インセンティブ・プレッシャーを与えているかどうかはわからない。
そういうわけでこの式をeの関数であると見なしてeで微分する。
するとβ-C'(e)となる。
努力水準をe上げるのは、最初はたやすいかも知れないが、どん
どん難しくなっていく。だから努力の費用C(e)はeが大きくなるに
つれ増加していく。
それに対してβが小さくなったり大きくなったりすると一様なイ
ンセンティブを与えることができなくなるから、βの値は常に、
β-C'(e)=0
を満たすように決めなければならない。
これを「インセンティブ制約式」と呼び、実現可能なインセンテ
ィブ雇用契約は、必ずこの式を満たさねばならないのである。
(つづく)
------------------------------------------------------------
今週の・・・
------------------------------------------------------------
計算式はややこしいけど、要するに常に努力するための費用の増
分とインセンティブ強度βが常に等しくなるように設定しなければ、
効率的な結果は得られないと言うことです。
たとえばものすごく努力しなければ結果がでないような場合、イ
ンセンティブ強度βはかなり大きくないと誰も努力しない。
これは激烈な競争をしているIT業界でストック・オプションが
多用される一つの原因である。
しかし少しの努力で結果がでるような場合、βを大きくすると企
業は利益を従業員に還元しすぎてしまう。
、、、ということです。
NEXT:インセンティブ契約のおさらい
インセンティブ契約のおさらい
http://hakase-jyuku.com/mare/category3-3/entry56.html
…
■努力水準とインセンティブ報酬制度
----------
さて、努力するにも何らかのコストがかかる。
業績アップのために本を読んだり英会話学校に通ったり、、或い
はその他の様々なトレーニングを行ったり、、、、
これらの費用をC(e)で表し、そしてIに
α(基本給)+β・(e+x+γy)
を代入して計算すると、インセンティブ契約における従業員の給料
(確実同値額)は、結局下のようになる。
w=α+βe-C(e)-(1/2)rβ^2・Var(x+γy)
(※ここでβ^2はβの二乗である。)
wは努力水準eの関数である(つまり従業員の努力いかんによっ
て給料が変化するわけだから)から、これをeで微分すると努力水
準と支払われる給料の上昇速度関係がはっきりする。
∂w/∂e=β-C'(e)
※C'(e)は努力一単位に必要な限界費用になる。
ここでβ-C'(e)>0だと、努力が大きい人はもの凄くたくさん
歩合をもらえることになり、小さい努力しかしない人はまるで実入
りが増えないことになってしまう。そしてまら企業は報酬を払いす
ぎることになる。
逆にβ-C'(e)<0だと、1努力した人は1もらえるが、10努力
したひとは7くらいしかもらえない事になる。
そう言うわけだから効率的なインセンティブ契約となるのは、
β-C'(e)=0となる場合である。
だからもし企業が従業員の努力水準を引き上げようと思うなら、
インセンティブ契約を結んだ上でβを引き上げなければならない。
この式を特に「インセンティブ制約」と呼び、実現可能な雇用契
約は必ずこの式を満たさねばならない。「インセンティブ両立的」
な契約は「インセンティブ制約」を満たす。
NEXT:インフォーマティブ原理
_____
ベン卜・ホルムストローム 2016ノーベル経済学賞
BREAKING 2016 Prize in Economic Sci. to Oliver Hart @Harvard & Bengt Holmström
@MIT “for their contributions to contract theory” #NobelPrize
Bengt Holmstrom, born 1949 in Helsinki, Finland.
Ph.D. 1978 from Stanford University, CA, USA.
Paul A. Samuelson Professor of Economics,
and Professor of Economics and Management at Massachusetts Institute of Technology, Cambridge, MA, USA.
《一九八〇年代後半には、経済学者のベン卜・ホルムストロームとポール・ミルグロム
により、もう一つの重要な研究結果が示された。両氏は数々の仮説に基づく極めて理論的
な論文において、通常は売上高にかかわらず歩合をー定に保つのが、営業担当者の報酬制
度として最適であると結論づけた。さまざまな種類のボーナスを設けたり、一定期間内に
目標を達成した人に以後は別の報酬体系を適用したりするなど、仕組みを複雑にしすぎる
と、担当者たちはそれにうまく乗じる方法を見つけ出すだろう、というのだ。
…
ホルムストロームとミルグロムが提案したようなシンプル極まりない報酬体系は、訴求
力がありそうに見えるが(理由のーつとして、運用しやすくコストもかさまない)、実際のと
ころ、多くの企業はもっと複雑な仕組みを選ぶ。「営業担当者はそれぞれ個性があり、モ
チべーションやニーズが異なるため、いくつもの要素から成る報酬体系のほうが幅広い層
にアピールするだろう」と考えるのだ。その理屈でいえば、個々の担当者から最高の成果
を引き出すには、個別に報酬体系を決めるべきだということになる。…》
(「営業を本気にさせる報酬制度とは」ダグ J.チュン ハーバード・ビジネス・スクール 助教授
DIAMONDハーバード・ビジネス・レビュー 2015年8/01号)
How to Really Motivate Salespeople
https://hbr.org/2015/04/how-to-really-motivate-salespeople
Another important study, from the late 1980s, came from the economists Bengt Holmstrom
and Paul Milgrom☆. In their very theoretical paper, which relies on a lot of assumptions, they
found that a formula of straight-line commissions (in which salespeople earn commissions
at the same rate no matter how much they sell) is generally the optimal way to pay reps.
They argue that if you make a sales comp formula too complicated—with lots of bonuses or
changes in commission structure triggered by hitting goals within a certain period—reps will
find ways to game it. The most common method of doing that is to play with the timing of
sales. If a salesperson needs to make a yearly quota, for instance, she might ask a friendly
client to allow her to book a sale that would ordinarily be made in January during the final
days of December instead (this is known as “pulling”); a rep who’s already hit quota, in contrast,
might be tempted to “push” December sales into January to get a head start on the next year’s goal.
☆
Aggregation and Linearity in the Provision of Intertemporal Incentives.(Adobe PDF)1987
Bengt Holmstrom Yale University Paul Milgrom Stanford University
https://faculty.fuqua.duke.edu/~qc2/BA532/1987%20EMA%20Holmstrom%20Milgrom.pdf 全27頁
邦訳組織の経済学267頁#7参照
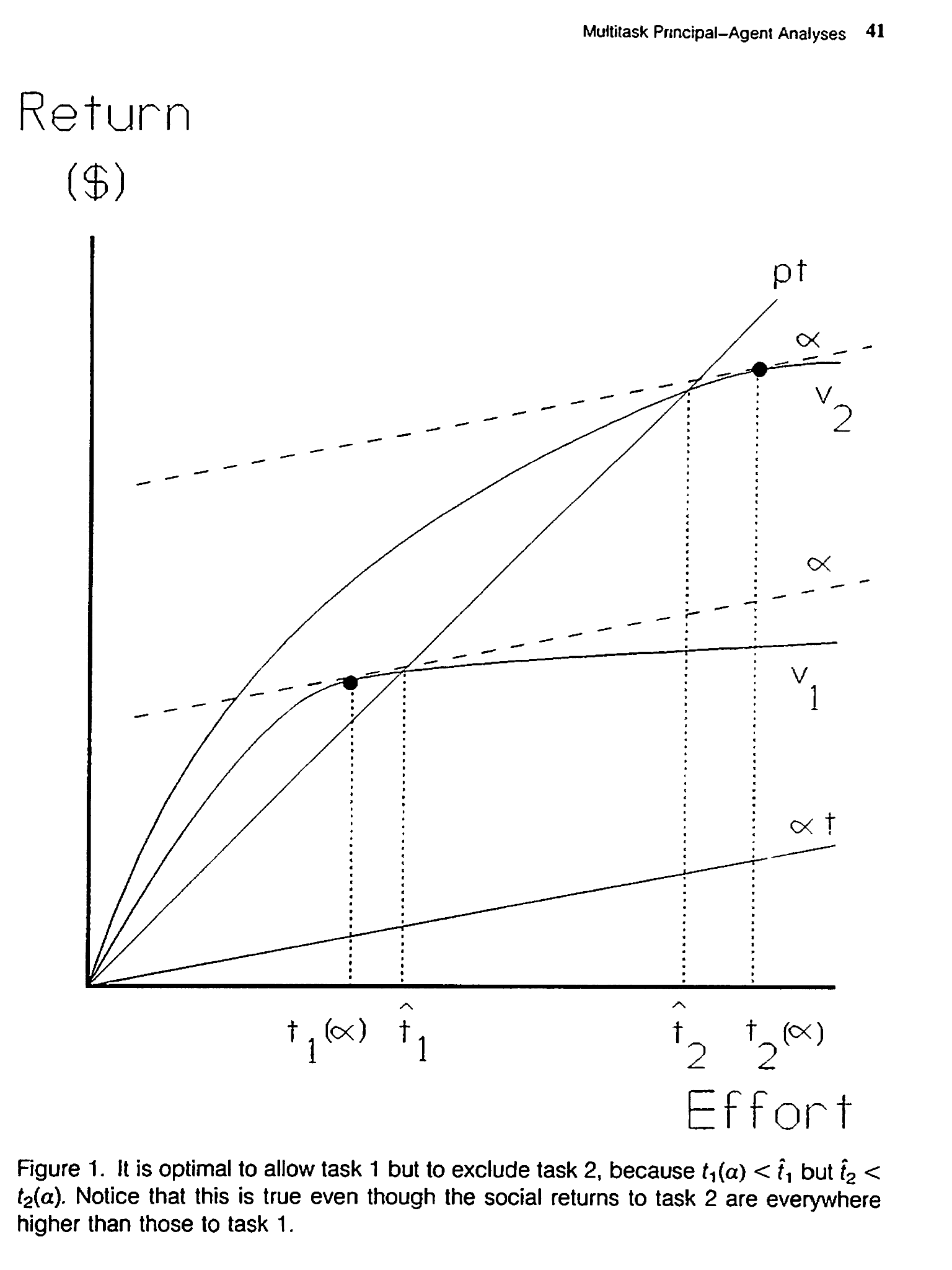
Multitask Principal-Agent Analyses: Incentive Contracts, Asset Ownership, and Job Design 1991
Bengt Holmstrom Yale University Paul Milgrom Stanford University
https://faculty.fuqua.duke.edu/~qc2/BA532/1991%20JLEO%20Holmstrom%20Milgrom.pdf 全30頁
------------------------------------------------------------
インセンティブ契約の実現可能性
------------------------------------------------------------
----------
■線型報酬関数を支える論理
----------
従業員に与えるインセンティブ報酬のモデルは eを努力水準、
xを需要水準(確率変数)、yをその産業全体に対する需要水準と
したとき
w(賃金)=α(基本給)+β・(e+x+γy)
であった。
もちろんこのような線型の式で表されるような報酬体系以外にも、
世の中には様々な形のインセンティブ契約が存在する。
たとえばセールスマンが一定以上の業績を挙げたときのみに支払
われる「成功報酬」である。
商品やサービスを売った分だけ歩合を与えるというやり方で、モ
ノを仕入れて売るだけの販社によくあるパターンである。
だがしかしこういう形式の契約には、大きな欠点がある。
それは
「最初につまづいて、その成功報酬をもらうための規準となる業績
に達しない見込みになるや否や、従業員のインセンティブが急激に
落ちる」
ということである。
与えられたノルマや達成水準に達しなければボーナス無し、とい
う条件下では、達成率30%も達成率99%も同じであるから、期
末に達成率が100%を越えなさそうだとわかった時点で従業員は
努力を止めて転職先を探し出し始めてしまう。
だからそういう契約ではなく、線型の歩合給の形でインセンティ
ブ契約を結ぶというのは、売り上げを伸ばすために一様なインセン
ティブを与えるために有効なのである。
線型の歩合給形式のインセンティブなら、期末に達成水準に達し
ないと分かった状態でも、次に一つ商品を売ったときに成功報酬を
受け取れるならセールスマンは商品を売ろうとするからである。
線型報酬関数に基づくインセンティブ契約は、そういうわけで従
業員に一様なインセンティブ・プレッシャーを与えることができ、
インセンティブ契約の最も良いモノの一つであると考えられる。
----------
■線型契約の下での総所得
----------
雇用主が中規模以上の企業の場合、従業員一人が担えるリスク負
担能力は、雇用主と比べて取るに足らないくらい小さい。
このため、インセンティブの問題を考えないとすれば、従業員の
給与に変動をもたらす全てのリスク発生源に対して保険を掛け、雇
用主が金銭的リスクを全部負担するのが最適であろう。
だがしかし、報酬中の全てのリスクを取り除いてしまうと、努力
水準を高めて利潤を増大させるインセンティブが、同時に従業員か
ら失われてしまう。
だから問題は(何度も書くが)リスク・シェアリングとインセン
ティブを与えバランスなのである。
さてここで、努力水準eと雇用主から与えられたインセンティブ
契約の規準となるパラメータα(固定給)、β(インセンティブ強
度)、γを考えてみる。
つまりベクトル(e、α、β、γ)によって、従業員の報酬が決
定されるようなインセンティブ契約を考えるわけである。
このとき従業員の確実同値額は、
「報酬の期待値」-「努力に要する費用」-「リスク・プレミアム」
となり、ゴチャゴチャ計算して簡素化すると、
α+βe-C(e)-(1/2)rβ^2・Var(x+γy)
となる。
そしてまた、同時に雇用主の確実同値額は、
「粗利潤の期待値」-「報酬支払い額の期待値」、つまり
P(e)-(α+βe)
である。
そういうわけで、従業員と雇用主の式を足しあわすと
「線型契約下における総所得」
が計算でき、それはつまり
P(e)-C(e)-(1/2)rβ^2・Var(x+γy)
ということになる。
----------
■努力インセンティブと、契約の実現可能性
----------
さて今、従業員の確実同値額は、
α+βe-C(e)-(1/2)rβ^2・Var(x+γy)
であった。
これはつまり従業員にとって収入が大きく変動すると困るから、
リスク・プレミアム分だけ安くていいから給料の基幹部分を固定給
にして、後はインセンティブ契約(つまり一部歩合給)で給与をも
らおうという仕組みである。
だからもし従業員に上手くインセンティブを与えて業績を伸ばそ
うと雇用主が考えるなら、従業員の努力水準eが、他のパラメータ
とどういう関係にあるか、確かめておかねばならない。
努力しても見返りがないなら、インセンティブ契約にはならない
から、βe-C(e)≧0は明らかであろう。がそれだけでは、適当な
インセンティブ・プレッシャーを与えているかどうかはわからない。
そういうわけでこの式をeの関数であると見なしてeで微分する。
するとβ-C'(e)となる。
努力水準をe上げるのは、最初はたやすいかも知れないが、どん
どん難しくなっていく。だから努力の費用C(e)はeが大きくなるに
つれ増加していく。
それに対してβが小さくなったり大きくなったりすると一様なイ
ンセンティブを与えることができなくなるから、βの値は常に、
β-C'(e)=0
を満たすように決めなければならない。
これを「インセンティブ制約式」と呼び、実現可能なインセンテ
ィブ雇用契約は、必ずこの式を満たさねばならないのである。
(つづく)
------------------------------------------------------------
今週の・・・
------------------------------------------------------------
計算式はややこしいけど、要するに常に努力するための費用の増
分とインセンティブ強度βが常に等しくなるように設定しなければ、
効率的な結果は得られないと言うことです。
たとえばものすごく努力しなければ結果がでないような場合、イ
ンセンティブ強度βはかなり大きくないと誰も努力しない。
これは激烈な競争をしているIT業界でストック・オプションが
多用される一つの原因である。
しかし少しの努力で結果がでるような場合、βを大きくすると企
業は利益を従業員に還元しすぎてしまう。
、、、ということです。
NEXT:インセンティブ契約のおさらい
インセンティブ契約のおさらい
http://hakase-jyuku.com/mare/category3-3/entry56.html
…
■努力水準とインセンティブ報酬制度
----------
さて、努力するにも何らかのコストがかかる。
業績アップのために本を読んだり英会話学校に通ったり、、或い
はその他の様々なトレーニングを行ったり、、、、
これらの費用をC(e)で表し、そしてIに
α(基本給)+β・(e+x+γy)
を代入して計算すると、インセンティブ契約における従業員の給料
(確実同値額)は、結局下のようになる。
w=α+βe-C(e)-(1/2)rβ^2・Var(x+γy)
(※ここでβ^2はβの二乗である。)
wは努力水準eの関数である(つまり従業員の努力いかんによっ
て給料が変化するわけだから)から、これをeで微分すると努力水
準と支払われる給料の上昇速度関係がはっきりする。
∂w/∂e=β-C'(e)
※C'(e)は努力一単位に必要な限界費用になる。
ここでβ-C'(e)>0だと、努力が大きい人はもの凄くたくさん
歩合をもらえることになり、小さい努力しかしない人はまるで実入
りが増えないことになってしまう。そしてまら企業は報酬を払いす
ぎることになる。
逆にβ-C'(e)<0だと、1努力した人は1もらえるが、10努力
したひとは7くらいしかもらえない事になる。
そう言うわけだから効率的なインセンティブ契約となるのは、
β-C'(e)=0となる場合である。
だからもし企業が従業員の努力水準を引き上げようと思うなら、
インセンティブ契約を結んだ上でβを引き上げなければならない。
この式を特に「インセンティブ制約」と呼び、実現可能な雇用契
約は必ずこの式を満たさねばならない。「インセンティブ両立的」
な契約は「インセンティブ制約」を満たす。
NEXT:インフォーマティブ原理
_____
ベン卜・ホルムストローム 2016ノーベル経済学賞
BREAKING 2016 Prize in Economic Sci. to Oliver Hart @Harvard & Bengt Holmström
@MIT “for their contributions to contract theory” #NobelPrize
Bengt Holmstrom, born 1949 in Helsinki, Finland.
Ph.D. 1978 from Stanford University, CA, USA.
Paul A. Samuelson Professor of Economics,
and Professor of Economics and Management at Massachusetts Institute of Technology, Cambridge, MA, USA.
《一九八〇年代後半には、経済学者のベン卜・ホルムストロームとポール・ミルグロム
により、もう一つの重要な研究結果が示された。両氏は数々の仮説に基づく極めて理論的
な論文において、通常は売上高にかかわらず歩合をー定に保つのが、営業担当者の報酬制
度として最適であると結論づけた。さまざまな種類のボーナスを設けたり、一定期間内に
目標を達成した人に以後は別の報酬体系を適用したりするなど、仕組みを複雑にしすぎる
と、担当者たちはそれにうまく乗じる方法を見つけ出すだろう、というのだ。
…
ホルムストロームとミルグロムが提案したようなシンプル極まりない報酬体系は、訴求
力がありそうに見えるが(理由のーつとして、運用しやすくコストもかさまない)、実際のと
ころ、多くの企業はもっと複雑な仕組みを選ぶ。「営業担当者はそれぞれ個性があり、モ
チべーションやニーズが異なるため、いくつもの要素から成る報酬体系のほうが幅広い層
にアピールするだろう」と考えるのだ。その理屈でいえば、個々の担当者から最高の成果
を引き出すには、個別に報酬体系を決めるべきだということになる。…》
(「営業を本気にさせる報酬制度とは」ダグ J.チュン ハーバード・ビジネス・スクール 助教授
DIAMONDハーバード・ビジネス・レビュー 2015年8/01号)
How to Really Motivate Salespeople
https://hbr.org/2015/04/how-to-really-motivate-salespeople
Another important study, from the late 1980s, came from the economists Bengt Holmstrom
and Paul Milgrom☆. In their very theoretical paper, which relies on a lot of assumptions, they
found that a formula of straight-line commissions (in which salespeople earn commissions
at the same rate no matter how much they sell) is generally the optimal way to pay reps.
They argue that if you make a sales comp formula too complicated—with lots of bonuses or
changes in commission structure triggered by hitting goals within a certain period—reps will
find ways to game it. The most common method of doing that is to play with the timing of
sales. If a salesperson needs to make a yearly quota, for instance, she might ask a friendly
client to allow her to book a sale that would ordinarily be made in January during the final
days of December instead (this is known as “pulling”); a rep who’s already hit quota, in contrast,
might be tempted to “push” December sales into January to get a head start on the next year’s goal.
☆
Aggregation and Linearity in the Provision of Intertemporal Incentives.(Adobe PDF)1987
Bengt Holmstrom Yale University Paul Milgrom Stanford University
https://faculty.fuqua.duke.edu/~qc2/BA532/1987%20EMA%20Holmstrom%20Milgrom.pdf 全27頁
邦訳組織の経済学267頁#7参照
Multitask Principal-Agent Analyses: Incentive Contracts, Asset Ownership, and Job Design 1991
Bengt Holmstrom Yale University Paul Milgrom Stanford University
https://faculty.fuqua.duke.edu/~qc2/BA532/1991%20JLEO%20Holmstrom%20Milgrom.pdf 全30頁
6章付録:インセンティブ契約の数学モデル より
表6.5 努力水準に対応した結果の確率
収入
行動 R=10 R=30
e=1 P=2/3 P=1/3
e=2 P=1/3 P=2/3









0 Comments:
コメントを投稿
<< Home