NAMs出版プロジェクト: 1月 2012

月曜日, 1月 30, 2012

Karinthy Frigyes　Lancszemek　フリジェシュ・カリンティ「鎖」1929

ネットワーク理論の最重要文献（フリジェシュ・カリンティ「鎖」『同じものは一つもない』1929年所収、英題"Chain-Links"）をハンガリー語原文で見つけた。
（→自動翻訳）英訳

https://nam-students.blogspot.com/2019/12/chain-links.html

カリンティが発見した、六次の隔たり理論（ろくじのへだたり、Six Degrees of Separation 人は自分の知り合いを6人以上介すと世界中の人々と間接的な知り合いになれる、という仮説）は、日本のSNSの草分け「グリー（Gree）」の語源にもなった。ちなみにカリンティの小説では6次ではなく５次のつながりという仮説になっている（起点を勘定に入れるか入れないかの違いだろうか？）。

政治的、時代的な背景もあるだろうが、ハンガリーにはグラフ理論の創始者エルデシュといい、こうした数学的思考を表現させる土壌があるようだ。

参考：
“A fascinating game grew out of this discussion. One of us suggested performing the following experiment to prove that the population of the Earth is closer together now than they have ever been before. We should select any person from the 1.5 billion inhabitants of the Earth—anyone, anywhere at all. He bet us that, using no more than five individuals, one of whom is a personal acquaintance, he could contact the selected individual using nothing except the network of personal acquaintances.”

It is taken from Chain-Links, written by Figyes Karinthy and translated from Hungarian with annotations by Adam Makkai and Enikö Jankó.
http://www.patrickthoffman.com/2008/05/27/following-up-the-small-world/

―-「今日、地球上の人々はかつてないほど互いに接近しあっている。そのことを証明するために、仲間の一人がある方法を提案した。その男は、地球上にいる15億の人から一人の名前を挙げてみたまえと言った。彼はたった五人の知人の輪を介して―しかもそのうちの一人は、彼が個人的に知っている人物だ―名前の挙がった人物にまで鎖をつなげてみせると言うのである」
―-
http://markezine.jp/article/detail/39

extra aroma 2
2011. augusztus 25., csütörtök
http://extraaroma2.blogspot.com/2011/08/karinthy-frigyes-lancszemek.html
以下上記ブログより転載。

＿＿＿＿＿＿＿＿＿＿＿＿＿

Karinthy Frigyes: Láncszemek

Egy döntő dolog igenis van – mondtam a vita hevében – (megint ezekről a hullámvonalakról volt szó, hogy fejlődik-e a világ, megy-e valamerre, vagy visszatérő ütemek játéka csak az egész, megújhodása a Mindigvoltnak) –, nem is tudom, hogy fejezzem ki, nem szeretek ismétlésbe esni. Talán így: soha még ilyen kicsike nem volt a Földgolyó, mint amilyenné mostanában lett – persze viszonylagosan. A szóbeli és fizikai közlekedés egyre gyorsuló irama összezsugorította a világot – elhiszem, hogy ez is volt már, az is volt már, mindenről volt már szó, de arról még nem volt szó soha, hogy amit gondolok, csinálok, amit akarok vagy szeretnék, arról – ha úgy tetszik neki vagy nekem – percek alatt értesül a Föld egész lakossága –, s ha személyesen akarok erről meggyőződni, napok alatt ott vagyok, hipp-hopp, ahol lenni akarok. Tündérország, ami a hétmérföldes csizmákat illeti, eljött e világra – némi csalódást csak annyiban hozott, hogy Tündérország sokkal kisebb országnak bizonyult, mint amilyen Valóság országa volt valaha. Chesterton azt írja valahol, nem érti, miért akarják a Kozmoszt mindenáron valami igen nagy dolognak elképzeltetni a metafizikusok – őneki jobban tetszik egy icike-picike, apart, hercig, intim kis világmindenség gondolata. Nagyon jellemzőnek találom ezt az ötletet a közlekedés századában – jellemzőbb, mint amennyire elmés vagy igaz, s éppen ezért, mert a reakciós tudomány- és technikatagadó, anti-evolucionista Chesterton volt vele kénytelen önkénytelenül elismerni, hogy az általa sokat emlegetett Tündérországot, íme mégiscsak az a bizonyos "tudományos" fejlődés varázsolta elő. Hát persze, minden visszatér és megújul – de nem veszitek észre, hogy ennek a visszatérésnek és megújulásnak a tempója gyorsul soha nem látott mértékben, térben és időben? Percek alatt kerüli meg gondolatom a glóbust – a világtörténelem fázisait évek alatt daráljuk le, mint a megunt leckét – ebből mégiscsak kijön valami, csak tudnám, mi? (Úgy rémlik, már-már szinte tudtam - de aztán elfelejtettem megint. Kételyek fogtak el – talán éppen azért, mert túl közel jártam az igazsághoz. A Sark közelében a mágnestű ingadozni kezd, tudjátok – úgy látszik, Isten közelében vagyunk így a hittel.)

Egyébként kedves játék alakult ki a vitából. Annak bizonyításául, hogy a Földgolyó lakossága sokkal közelebb van egymáshoz, mindenféle tekintetben, mint ahogy valaha is volt, próbát ajánlott fel a társaság egyik tagja. Tessék egy akármilyen meghatározható egyént kijelölni a Föld másfél milliárd lakója közül, bármelyik pontján a Földnek – ő fogadást ajánl, hogy legföljebb öt más egyénen keresztül, kik közül az egyik neki személyes ismerőse, kapcsolatot tud létesíteni az illetővel, csupa közvetlen – ismeretség – alapon, mint ahogy mondani szokták: "Kérlek, te ismered X. Y.-t, szólj neki, hogy szóljon Z. V.-nek, aki neki ismerőse..." stb.

– Na, erre kíváncsi vagyok – mondta valaki –, hát kérem, mondjuk... mondjuk, Lagerlöf Zelma.

– Lagerlöf Zelma – mondta barátunk –, mi sem könnyebb ennél.

Két másodpercig gondolkodott csak, már kész is volt. Hát kérem, Lagerlöf Zelma, mint a Nobel-díj nyertese, nyilván személyesen ismeri Gusztáv svéd királyt, hiszen az adta át neki a díjat, az előírás szerint. Márpedig Gusztáv svéd király szenvedélyes teniszjátékos, részt vesz a nemzetközi nagy versenyeken is, játszott Kehrlinggel, akit kétségkívül kegyel és jól ismer – Kehrlinget pedig én magam (barátunk szintén erős teniszjátékos) nagyon jól ismerem. Íme a lánc – csak két láncszem kellett hozzá a maximális öt pontból, ami természetes is, hiszen a világ nagy hírű és népszerű embereihez könnyebb kapcsolatot találni, mint a jelentéktelenséghez, lévén előbbieknek rengeteg ismerőse. Tessék nehezebb feladatot adni.

A nehezebb feladatot: egy szögecselő munkást a Ford-művek műhelyéből, ezek után magam vállaltam, és négy láncszemmel szerencsésen meg is oldottam. A munkás ismeri műhelyfőnökét, műhelyfőnöke magát Fordot, Ford jóban van a Hearst-lapok vezérigazgatójával, a Hearst-lapok vezérigazgatójával tavaly alaposan összeismerkedett Pásztor Árpád úr, aki nekem nemcsak ismerősöm, de tudtommal kitűnő barátom – csak egy szavamba kerül, hogy sürgönyözzön a vezérigazgatónak, hogy szóljon Fordnak, hogy Ford szóljon a műhelyfőnöknek, hogy az a szögecselő munkás sürgősen szögecseljen nekem össze egy autót, éppen szükségem lenne rá.

Így folyt a játék, és barátunknak igaza lett – soha nem kellett ötnél több láncszem ahhoz, hogy a Földkerekség bármelyik lakosával, csupa személyes ismeretség révén, összeköttetésbe kerüljön a társaság bármelyik tagja. Mármost felteszem a kérdést – volt-e valaha kora a történelemnek, amikor ez lehetséges lett volna? Julius Caesar hatalmas ember volt, de ha például eszébe jut, hogy az akkori Amerika valamelyik azték- vagy maya-törzsbeli papjához néhány órán vagy néhány napon belül protekciót szerezzen – ezt a tervét nem öt, hanem háromszáz láncszemen keresztül sem tudta volna megvalósítani, már csak azért sem, mert hiszen Amerikáról és annak lehetséges vagy nem lehetséges lakosairól kevesebbet tudtak abban az időben, mint amennyit mi a Marsról és annak lakosairól tudunk.

Valami van, valami folyamat, ritmuson és hullámon túl – szűkülés és tágulás. Valami összemegy, és kisebb lesz, és valami szétárad, és egyre nagyobbodik. Lehetséges – lehetséges volna mégis –, hogy ez az összemenés és kisebbedés – hogy ez a fizikai világ és ez a Szétáradás és Nagyobbodás ezzel a pislákoló kis szikrával kezdődött, ami sok millió évvel ezelőtt gyulladt ki az ember-állat idegkocsonyájában – hogy szétáradva és nagyobbodva és mindent fölégetve, ami útjába kerül, lángba borítsa és összezsugorítsa és hamuvá égesse az egész fizikai világot? Lehetséges – hát mégis lehetséges volna, hogy az erő legyőzi az anyagot – hogy a lélek erősebb és igazabb igazság, mint a test – hogy az életnek értelme van, mely túléli az életet – hogy a jó túléli a rosszat, az élet túléli a halált –, hogy Isten mégis hatalmasabb az ördögnél?

Mert, kérem – restelkedve vallom be, bocsánatot is kérek érte, és tiltakozom ellene, hogy azért bolondnak tartsanak – ezen a protekciós játékon még mindig gyakran kapom magam rajta, nemcsak emberek, hanem dolgok összefüggésében is. Sajnos, magától megy ez már nálam, mint a köhögés. Haszontalan játék, semmit sem tudok vele megváltoztatni – hiába, úgy vagyok vele, mint a játékos, aki mindenét elvesztette kártyabarlangjaiban: de inkább babra játszik tovább, vagy csak úgy semmibe, nyerés reménye nélkül: csak a kártya négy színét láthassa. Reménytelenül zakatol bennem a Gondolat furcsa játéka – két láncszemmel, három láncszemmel, legfeljebb öt láncszemmel, hogy kaphatnék kapcsolatot, összefüggést az élet elém kerülő apró-cseprő dolgai közt – hogy akasszam össze egyik jelenséget a másikkal – a viszonylagost, az elmúlót hogy hozzam vonatkozásba a nem viszonylagossal és maradóval – a részt hogy kössem össze az egésszel? Jó lenne élni, élvezni, örülni, venni a dolgokat csak abban a vonatkozásban, ahogy örömömet szolgálják, vagy fájdalmat okoznak – hiába! izgat a játék, hogy a rám nevető szemben, a felém sújtó ökölben egyebet is keressek, mint amennyi elég, hogy odahúzzam magamhoz vagy védekezzek ellene. Valaki szeret – valaki haragszik rám –-, miért szeret, miért haragszik? Ketten nem értik egymást – nekem meg kell érteni mindkettőt –, de hogyan? Szőlőt árulnak az utcán – kisfiam sír a másik szobában. Ismerősurat megcsalta a felesége – a Dempsey-mérkőzésen százötvenezer ember üvöltött – Romain Rolland új könyve nem kellett senkinek – X. barátom megváltoztatta véleményét Y-ról – lánc-lánc-eszterlánc, hogy lehetne e zagyvaságban összekötő vonalat lelni? mégpedig gyorsan és közvetlenül, nem harminc kötet filozófiával! Legfeljebb következtetéssel, mégis úgy, hogy a lánc, ami a dologból indul utolsó láncszemével minden dolgok forrásához, önmagamhoz vezessen. Mint ahogy...

Mint ahogy ez az úr... ez az úr, aki idejött az asztalomhoz... ahol ezt írom, idejött és megzavart, valami jelentéktelen ügyes-bajos dolgával: kiverte fejemből, amit éppen mondani akartam. Miért jött ide, hogy mert megzavarni? Első láncszem: nem sokra tartja az egész irkafirkát. De miért? Második láncszem: általában nem becsülik annyira az irkafirkát világszerte, mint csak negyedszázaddal ezelőtt. Ennek az a világrengés az oka, mely a Szellemet kompromittálta – ha csak ez jött ki belőle, ami kijött, nem sokat érhetett a századvég híres eszmeáradata, "világszemlélete". Harmadik láncszem: ezért uralkodik Európa fölött a Félelem és Erőszak felszabadult hisztériája, felbomlott a Rend – negyedik láncszem!

Jöjjön hát az új Rend, jöjjön el a világ új megváltója, mutassa meg magát újra a világ Istene égő csipkebokorban, legyen béke, legyen háború, legyen forradalom, hogy – ó, ötödik láncszem! – ne történhessen meg újra, hogy valaki engem zavarni merészeljen, mikor játszom, mikor képzelődöm, mikor gondolkodom!

----------------------------------------------------------------

ちなみに、英訳は以下に所収され２００６年に出版されている。
The structure and dynamics of networks 著者: Mark E. J. Newman,Albert-László Barabási,Duncan J. Watts
googlebooksでは一頁以外読むことができる。

「25」

something else in the eyes that smile at me or the fist that strikes
me, something beyond the urge to draw near to the former and
shy away from the latter, One person loves me， another hates me，
Why? Why the love and the hatred？

There are two people who do not understand one another, but I'm
supposed to understand both. How? Someone is selling grapes in
the street while my young son is crying in the other room，An
acquaintance's wife has cheated on him while a crowd of
hundred and flfty thousand watches the Dempsey match, Romain
Roland's (3) last novel bombed while my friend Q changes his
mind about Mr. Y. Ring-a-ring o' roses, a pocketful of posies.
How　can　one possibly construct　any chain　of connections
between these random things, without filling thirty volumes of
philosophy, making only reasonable suppositions. The chain
starts with the matter, and its last link leads to me, as the source
of everything.

WeII, just like this gentleman, who stepped up to my table in the
cafe where l am now writing，He walked up to me and
interrupted my thoughts with some trifling, insignificant problem
and made me forget what l was going to say. Why did he come
here and disturb me? The first link: he doesn't think much of
people he finds scribbling， The second link: this world doesn't
value scribbling nearly as much as it used to just a quarter of a
century ago， The famous world-views and thoughts that marked
the end of the 19th century are to no avail today. Now we disdain
the intellect. The third link: this disdain is the source of the
hysteria of fear and terror that grips Europe today， And so to the
fourth link: the order of the world has been destroyed，

Well，then，let a New World order appear! Let the new Messiah
of the world come! Let the God of the universe show himself
once more through the burning rosehip-bush! Let there be peace,
let there be war， let there be revolutions， so that ー and here is

______________

3　Romain Roland， the noted French novelist, lived from 1866 until 1944. He
was awarded the NobeI Prize for literature in 1915, Nearly all of his works
were translated into Hungarian, just as in the case of Selma Lagerlof.

＿＿＿＿＿＿＿＿＿＿＿

http://nam-students.blogspot.jp/2012/01/karinthy-frigyeslancszemek1929.html: 「21」

CHAIN - LINKS

　　　by

　Frigyes Karinthy

We were arguing energetically about whether the world is
actually evolving, headed in a particular direction, or whether the
entire universe is just a returning rhythm's game， a renewal of
eternity. "There has to be something of crucial importance," I
said in the middle of debate. I just don't quite know how to
express it in a new way; I hate repeating myself."

Let me put it this way: Planet Earth has never been as tiny as it is
now. It shrunk － relatively speaking of course － due to the
quickening pulse of both physical and verbal communication，
This topic has come up before, but we had never named it quite
this way. We never talked about the fact that anyone on Earth, at
my or anyone's will, can now learn in just a few minutes what I
think or do, and what l want or what l would like to do. If I
wanted to convince myself of the above fact: in couple of days, I
could be － Hocus pocus! － where I want to be.

Now we live in fairyland. The only slightly disappointing thing
about this land is that it is smaller than the real world has ever
been.

「22」

Chesterton praised a tiny and intimate, small universe and found
it obtuse to portray the Cosmos as something very big. l think
this idea is peculiar to our age of transportation. While
Chesterton rejected technology and evolution, he was finally
forced to admit that the fairyland he dreamed of could only come
about through the scientific revolution he so vehemently
opposed.

Everything returns and renews itself. The difference now is that
the rate of these returns has increased, in both space and time, in
an unheard-of fashion. Now my thoughts can circle the globe in
minutes. Entire passages of world history are played out in a
couple of years.

Something must result from this chain of thoughts. If only I knew
what! (I feel as if I knew the answer to all this，but I've forgotten
what it was or was overcome with doubt. Maybe I was too close
to the truth. Near the North Pole， they say， the needle of a
compass goes haywire， turning around in circles. It seems as if
the same thing happens to our beliefs when we get too close to
God.)

A fascinating game grew out of this discussion. One of us
suggested performing the following experiment to prove that the
population of the Earth is closer together now than they have
ever been before. We should select any person from the 1.5
billion inhabitants of the Earth － anyone， anywhere at all. He bet
us that， using no more than five individuals, one of whom is a
personal acquaintance, he could contact the selected individual
using nothing except the network of personal acquaintances. For
example，“Look，you know Mr. X.Y.，please ask him to contact
his friend Mr.Q.Z.,whom he knows, and so forth.”
“An interesting idea!” － someone said － “Let’s give it a try，
How would you contact Selma Lagerlöf?”(1)

＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

1　Swedish novelist Selma Lagerlöf(1858－1940)，who received the Nobel
Prize for literature in 1909, was a champion of the return or Swedish
romanticism with a mystical overtone. She also wrote novels for children.; 「23」

“Well now， Selma Lagerlöf, " the proponent of the game replied，
“Nothing could be easier." And he reeled off a solution in two
seconds:　“Selma Lagerlöf just　won　the　Nobel　Prize for
Literature， so she's bound to know King Gustav of Sweden，
since, by rule, he's the one who would have handed her the Prize，
And it's well known that King Gustav loves to play tennis and
participates in international tennis tournaments. He has played
Mr. Kehrling(2) so they must be acquainted. And as it happens I
myself also know Mr. Kehrling quite well." (The proponent was
himself a good tennis player. “ All we needed this time was two
out of five links. That's not surprising since it's always easier to
find someone who knows a famous or popular figure than some
run-of-the-mill， insignificant person. Come on, give me a harder
one to solve!"

I proposed a more difficult problem: to find a chain of contacts
linking myself with an anonymous riveter at the Ford Motor
Company － and I accomplished it in four steps. The worker
knows his foreman，who knows Mr. Ford himself, who， in turn，
is on good terms with the director general　of the　Hearst
publishing empire， I had a close friend， Mr. Árpád Pásztor, who
had recently struck up an acquaintance with the director of
Hearst publishing，It would take but one word to my friend to
send a cable to the general director of Hearst asking him to
contact Ford who could in turn contact the foreman, who could
then　contact the riveter，who　could then　assemble　a new
automobile for me, should I need one.

And so the game went on. Our friend was absolutely correct:
nobody from the group needed more than five links in the chain
to reach, just by using the method of acquaintance， any inhabitant
of our Planet.

＿＿＿＿＿＿＿＿＿＿＿＿＿＿

2　Bel Kehrling，（1891－1937）was a noted Hungarian sportsman, soccer，
ping-pong and tennis player. In tennis， he emerged victorious in l923 in
Gothenberg，Sweden，both indoors and in the open; he placed third in the
Wimbledon doubles. He also played soccer and ice hockey.
「24」

And this leads us to another question: Was there ever a time in
human history when this would have been impossible? Julius
Caesar，for instance， was a popular man， but if he had got it into
his head to try and contact a priest from one of the Mayan or
Aztec tribes that lived in the Americas at that time， he could not
have succeeded － not in five steps， not even in three hundred.
Europeans in those days knew less about America and its
inhabitants than we now know about Mars and its inhabitants.

So something is going on here， a process of contraction and
expansion which is beyond rhythms and waves. Something
coalesces，shrinks in size， while something else flows outward
and grows. How is it possible that all this expansion and material
growth can have started with a tiny， glittering speck that flared
up millions of years ago in the mass of nerves in a primitive
human's head? And how is it possible that by now， this
continuous growth has the inundating ability to reduce the entire
physical world to ashes? Is it possible that power can conquer
matter， that the soul makes a mightier truth than the body, that
life has a meaning that survives life itself; that good survives evil
as life survives death, that God， after all， is more powerful than
the Devil?

I am embarrassed to admit － since it would look foolish － that
I often catch myself playing our well-connected game not only
with human beings， but with objects as well. I have become very
good at it. It's a useless game, of course, but I think I'm addicted
to it，like a gambler who, having lost all of his money, plays for
dried beans without any hope of real gain － just to see the four
colors of the cards. The strange mind-game that clatters in me all
the time goes like this: how can I link, with three, four, or at most
five links of the chain, trivial，everyday things of life. How can I
link one phenomenon to another? How can I join the relative and
the ephemeral with steady, permanent things － how can I tie up
the part with the whole？

It would be nice to just live, have fun, and take notice only of the
utility of things: how much pleasure or pain they cause me. Alas，
it's not possible. I hope that this game will help me find
「25」

something else in the eyes that smile at me or the fist that strikes
me, something beyond the urge to draw near to the former and
shy away from the latter, One person loves me， another hates me，
Why? Why the love and the hatred？

There are two people who do not understand one another, but I'm
supposed to understand both. How? Someone is selling grapes in
the street while my young son is crying in the other room，An
acquaintance's wife has cheated on him while a crowd of
hundred and fifty thousand watches the Dempsey match, Romain
Roland's (3) last novel bombed while my friend Q changes his
mind about Mr. Y. Ring-a-ring o' roses, a pocketful of posies.
How　can　one possibly construct　any chain　of connections
between these random things, without filling thirty volumes of
philosophy, making only reasonable suppositions. The chain
starts with the matter, and its last link leads to me, as the source
of everything.

Well, just like this gentleman, who stepped up to my table in the
cafe where l am now writing，He walked up to me and
interrupted my thoughts with some trifling, insignificant problem
and made me forget what l was going to say. Why did he come
here and disturb me? The first link: he doesn't think much of
people he finds scribbling， The second link: this world doesn't
value scribbling nearly as much as it used to just a quarter of a
century ago， The famous world-views and thoughts that marked
the end of the 19th century are to no avail today. Now we disdain
the intellect. The third link: this disdain is the source of the
hysteria of fear and terror that grips Europe today， And so to the
fourth link : the order of the world has been destroyed.

Well，then，let a New World order appear! Let the new Messiah
of the world come! Let the God of the universe show himself
once more through the burning rosehip-bush! Let there be peace,
let there be war， let there be revolutions， so that － and here is

______________

3　Romain Roland， the noted French novelist, lived from 1866 until 1944. He
was awarded the Nobel Prize for literature in 1915, Nearly all of his works
were translated into Hungarian, just as in the case of Selma Lagerlöf.

「26」

the fifth link － it cannot happen again that someone should dare
disturb me when I am at play. when set free the phantoms of
my imagination, when I think !

　　　　　　　　　Translated from Hungarian and annotated by
　　　　　　　　　　　　　　　　　Adam Makkai
　　　　　　　　　　　　　　　Edited by Eniko Janko

日曜日, 1月 29, 2012

Raum und Zeit (Minkowski) 1908

＜世界点x、y、z、t、に存在する実体的な点に注目し、この実体点をすべての異なった時刻に再び認知できると考える。この実体点の空間座標の変化dx、dy、dzは、時間要素dtに対するとする。そうすると、実体点のいわば永遠の人生行路の像として世界の中の一本の曲線すなわち世界線が得られる。その点は−∞から＋∞までのパラメータt に一義的に関係づけられる。私は今ここで、物理法則の最も完全な表現は、私の考えでは、この世界線の間の相互関係という形をとらねばならないという予想を立てたいのである。＞ミンコフスキー　1908

http://ja.wikipedia.org/wiki/ミンコフスキー空間
http://de.wikisource.org/wiki/Raum_und_Zeit_%28Minkowski%29

　　　　　　　　　　　Raum und Zeit
　　　　　　　　　　　空間と時間
　　　　　　　
　　　　　　　　　　　　　　　　Hermann Minkowski, Göttingen
　　　　　　　　　　　　　　　　ハーマン・ミンコフスキー

M. H.! Die Anschauungen über Raum und Zeit, die ich Ihnen entwickeln möchte, sind auf experimentell-physikalischem Boden erwachsen. Darin liegt ihre Stärke. Ihre Tendenz ist eine radikale. Von Stund′ an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.

　皆さん！　私があなたがたに説明したいと思う空間と時間についての見方
は、実験物理学の土壌に成長したもので、そこにその強さがある。それの傾
向はラディカルなものである。今からは，空間それ自体や時間それ自体は完
全に陰に沈み、両者の一種の統合だけが独立性を保つことになるだろう。

Raum und Zeit (Minkowski)

1908

邦訳
空間と時間

『相対論』東海大学出版会１９６９年

→自動翻訳、英語版（http://en.wikisource.org/wiki/Space_and_Time、英語版自動翻訳）

[1] M. H.! Die Anschauungen über Raum und Zeit, die ich Ihnen entwickeln möchte, sind auf experimentell-physikalischem Boden erwachsen. Darin liegt ihre Stärke. Ihre Tendenz ist eine radikale. Von Stund′ an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.

I.
Ich möchte zunächst ausführen, wie man von der gegenwärtig angenommenen Mechanik wohl durch eine rein mathematische Überlegung zu veränderten Ideen über Raum und Zeit kommen könnte. Die Gleichungen der Newtonschen Mechanik zeigen eine zweifache Invarianz. Einmal bleibt ihre Form erhalten, wenn man das zugrunde gelegte räumliche Koordinatensystem einer beliebigen Lagenveränderung unterwirft, zweitens, wenn man es in seinem Bewegungszustande verändert, nämlich ihm irgendeine gleichförmige Translation aufprägt; auch spielt der Nullpunkt der Zeit keine Rolle. Man ist gewohnt, die Axiome der Geometrie als erledigt anzusehen, wenn man sich reif für die Axiome der Mechanik fühlt, und deshalb werden jene zwei Invarianzen wohl selten in einem Atemzuge genannt. Jede von ihnen bedeutet eine gewisse Gruppe von Transformationen in sich für die Differentialgleichungen der Mechanik. Die Existenz der ersteren Gruppe sieht man als einen fundamentalen Charakter des Raumes an. Die zweite Gruppe straft man am liebsten mit Verachtung, um leichten Sinnes darüber hinwegzukommen, daß man von den physikalischen Erscheinungen her niemals entscheiden kann, ob der als ruhend vorausgesetzte Raum sich nicht am Ende in einer gleichförmigen Translation befindet. So führen jene zwei Gruppen ein völlig getrenntes Dasein nebeneinander. Ihr gänzlich heterogener Charakter mag davon abgeschreckt haben, sie zu komponieren. Aber gerade die komponierte volle Gruppe als Ganzes gibt uns zu denken auf.

Wir wollen uns die Verhältnisse graphisch zu veranschaulichen suchen. Es seien $x,\, y,\, z$ rechtwinklige Koordinaten für den Raum, und $t\!$ bezeichne die Zeit. Gegenstand unserer Wahrnehmung sind immer nur Orte und Zeiten verbunden. Es hat niemand einen Ort anders

[2] bemerkt als zu einer Zeit, eine Zeit anders als an einem Orte. Ich respektiere aber noch das Dogma, daß Raum und Zeit je eine unabhängige Bedeutung haben. Ich will einen Raumpunkt zu einem Zeitpunkt, d. i. ein Wertsystem $x,\,y,\,z,\,t$ einen Weltpunkt nennen. Die Mannigfaltigkeit aller denkbaren Wertsysteme $x,\,y,\,z,\,t$ soll die Welt heißen. Ich könnte mit kühner Kreide vier Weltachsen auf die Tafel werfen. Schon eine gezeichnete Achse besteht aus lauter schwingenden Molekülen und macht zudem die Reise der Erde im All mit, gibt also bereits genug zu abstrahieren auf; die mit der Anzahl 4 verbundene etwas größere Abstraktion tut dem Mathematiker nicht wehe. Um nirgends eine gähnende Leere zu lassen, wollen wir uns vorstellen, daß aller Orten und zu jeder Zeit etwas Wahrnehmbares vorhanden ist. Um nicht Materie oder Elektrizität zu sagen, will ich für dieses Etwas das Wort Substanz brauchen. Wir richten unsere Aufmerksamkeit auf den im Weltpunkt $x,\,y,\,z,\,t$ vorhandenen substantiellen Punkt und stellen uns vor, wir sind imstande, diesen substantiellen Punkt zu jeder anderen Zeit wieder zu erkennen. Einem Zeitelement $dt\!$ mögen die Änderungen $dx,\,dy,\,dz$ der Raumkoordinaten dieses substantiellen Punktes entsprechen. Wir erhalten alsdann als Bild sozusagen für den ewigen Lebenslauf des substantiellen Punktes eine Kurve in der Welt, eine Weltlinie, deren Punkte sich eindeutig auf den Parameter $t\!$ von $-\infty\!$ bis $+\infty\!$ beziehen lassen. Die ganze Welt erscheint aufgelöst in solche Weltlinien, und ich möchte sogleich vorwegnehmen, daß meiner Meinung nach die physikalischen Gesetze ihren vollkommensten Ausdruck als Wechselbeziehungen unter diesen Weltlinien finden dürften.

Durch die Begriffe Raum und Zeit fallen die $x,\, y,\, z$ -Mannigfaltigkeit $t=0\!$ und ihre zwei Seiten $t>0\!$ und $t<0\!$ auseinander. Halten wir der Einfachheit wegen den Nullpunkt von Raum und Zeit fest, so bedeutet die zuerst genannte Gruppe der Mechanik, daß wir die $x,\, y,\, z$ -Achsen in $t=0\!$ einer beliebigen Drehung um den Nullpunkt unterwerfen dürfen, entsprechend den homogenen linearen Transformationen des Ausdrucks

$x^2+y^2+z^2\,$

in sich. Die zweite Gruppe aber bedeutet, daß wir, ebenfalls ohne den Ausdruck der mechanischen Gesetze zu verändern,

$x, \, y, \, z, \, t$ durch $x - \alpha t ,\, y - \beta t ,\, z - \gamma t, t$

mit irgendwelchen Konstanten $\alpha,\, \beta,\, \gamma$ ersetzen dürfen. Der Zeitachse kann hiernach eine völlig beliebige Richtung nach der oberen halben Welt $t>0\!$ gegeben werden. Was hat nun die Forderung der Orthogonalitat

[3] im Raume mit dieser völligen Freiheit der Zeitachse nach oben hin zu tun?

Die Verbindung herzustellen, nehmen wir einen positiven Parameter $c\!$ und betrachten das Gebilde

$c^2t^2 - x^2 - y^2 -z^2 =1.\,$

Es besteht aus zwei durch $t=0\!$ getrennten Schalen nach Analogie eines zweischaligen Hyperboloids. Wir betrachten die Schale im Gebiete $t>0\,,$ und wir fassen jetzt diejenigen homogenen linearen Transformationen von $x,\,y,\,z,\,t$ in vier neue Variable $x',\,y',\,z',\,t'$ auf, wobei der Ausdruck dieser Schale in den neuen Variabeln entsprechend wird. Zu diesen Transformationen gehören offenbar die Drehungen des Raumes um den Nullpunkt. Ein volles

Fig. 1.

Verständnis der übrigen jener Transformationen erhalten wir hernach bereits, wenn wir eine solche unter ihnen ins Auge fassen, bei der $y\!$ und $z\!$ ungeändert bleiben. Wir zeichnen (Fig. 1) den Durchschnitt jener Schale mit der Ebene der $x\!$ - und der $t\!$ -Achse, den oberen Ast der Hyperbel $c^2t^2 - x^2=1\,,$ mit seinen Asymptoten. Ferner werde ein beliebiger Radiusvektor $OA'\!$ dieses Hyperbelastes vom Nullpunkte $O\!$ aus eingetragen, die Tangente in $A'\!$ an die Hyperbel bis zum Schnitte $B'\!$ mit der Asymptote rechts gelegt, $OA'B'\!$ zum Parallelogramm $OA'B'C'\!$ vervollständigt, endlich für das spätere noch $B'C'\!$ bis zum Schnitt $D'\!$ mit der $x\!$ -Achse durchgeführt. Nehmen wir nun $OC'\!$ und $OA'\!$ als Achsen für Parallelkoordinaten $x',\,t'\!$ mit den Maßstäben $OC'=1,\, OA'= 1/c\,,$ so erlangt jener Hyperbelast wieder den Ausdruck $c^2t'^2-x'^2=1, t'>0\!\,,$ und der Übergang von $x,\,y,\,z,\,t$ zu $x',\,y,\,z,\,t'$ ist eine der fraglichen Transformationen. Wir nehmen nun zu den charakterisierten Transformationen noch die beliebigen Verschiebungen des Raum- und Zeit-Nullpunktes hinzu und konstituieren damit eine offenbar noch von dem Parameter $c\!$ abhängige Gruppe von Transformationen, die ich mit $G_c\!$ bezeichne.

Lassen wir jetzt $c\!$ ins Unendliche wachsen, also $1/c\!$ nach Null konvergieren, so leuchtet an der beschriebenen Figur ein, daß der Hyperbelast sich immer mehr der $x\!$ -Achse anschmiegt, der Asymptotenwinkel sich zu einem gestreckten verbreitert, jene spezielle Transformation in der Grenze sich in eine solche verwandelt, wobei die $t'\!$ -Achse eine beliebige Richtung nach oben haben kann und $x'\!$ immer genauer sich an $x\!$ annähert. Mit Rücksicht hierauf ist klar, daß aus der

[4] Gruppe $G_c\!$ in der Grenze für $c=\infty\,,$ also als Gruppe $G_\infty\,,$ eben jene zu der Newtonschen Mechanik gehörige volle Gruppe wird. Bei dieser Sachlage, und da $G_c\!$ mathematisch verständlicher ist als $G_\infty\,,$ hätte wohl ein Mathematiker in freier Phantasie auf den Gedanken verfallen können, daß am Ende die Naturerscheinungen tatsächlich eine Invarianz nicht bei der Gruppe $G_\infty\,,$ sondern vielmehr bei einer Gruppe $G_c\!$ mit bestimmtem endlichen, nur in den gewöhnlichen Maßeinheiten äußerst großen $c\!$ besitzen. Eine solche Ahnung wäre ein außerordentlicher Triumph der reinen Mathematik gewesen. Nun, da die Mathematik hier nur mehr Treppenwitz bekundet, bleibt ihr doch die Genugtuung, daß sie dank ihren glücklichen Antezedenzien mit ihren in freier Fernsicht geschärften Sinnen die tiefgreifenden Konsequenzen einer solcher Ummodelung unserer Naturauffassung auf der Stelle zu erfassen vermag.

Ich will sogleich bemerken, um welchen Wert für $c\!$ es sich schließlich handeln wird. Für $c\!$ wird die Fortpflanzungsgeschwindigkeit des Lichtes im leeren Raume eintreten. Um weder vom Raum noch von Leere zu sprechen, können wir diese Größe wieder als das Verhältnis der elektrostatischen und der elektromagnetischen Einheit der Elektrizitätsmenge kennzeichnen.

Das Bestehen der Invarianz der Naturgesetze für die bezügliche Gruppe $G_c\!$ würde nun so zu fassen sein:

Man kann aus der Gesamtheit der Naturerscheinungen durch sukzessiv gesteigerte Approximationen immer genauer ein Bezugsystem $x,\,y,\,z$ und $t\,,$ Raum und Zeit, ableiten, mittels dessen diese Erscheinungen sich dann nach bestimmten Gesetzen darstellen. Dieses Bezugsystem ist dabei aber durch die Erscheinungen keineswegs eindeutig festgelegt. Man kann das Bezugsystem noch entsprechend den Transformationen der genannten Gruppe $G_c\!$ beliebig verändern, ohne daß der Ausdruck der Naturgesetze sich dabei verändert.

Z. B. kann man der beschriebenen Figur entsprechend auch $t'\!$ Zeit benennen, muß dann aber im Zusammenhange damit notwendig den Raum durch die Mannigfaltigkeit der drei Parameter $x',\,y,\,z$ definieren, wobei nun die physikalischen Gesetze mittels $x',\,y,\,z,\,t'$ sich genau ebenso ausdrücken würden, wie mittels $x,\,y,\,z,\,t.$ Hiernach würden wir dann in der Welt nicht mehr den Raum, sondern unendlich viele Räume haben, analog wie es im dreidimensionalen Räume unendlich viele Ebenen gibt. Die dreidimensionale Geometrie wird ein Kapitel der vierdimensionalen Physik. Sie erkennen, weshalb ich am Eingange sagte, Raum und Zeit sollen zu Schatten herabsinken und nur eine Welt an sich bestehen.

[5]

II.
Nun ist die Frage, welche Umstände zwingen uns die veränderte Auffassung von Raum und Zeit auf, widerspricht sie tatsächlich niemals den Erscheinungen, endlich gewährt sie Vorteile für die Beschreibung der Erscheinungen?

Bevor wir hierauf eingehen, sei eine wichtige Bemerkung vorangestellt. Haben wir Raum und Zeit irgendwie individualisiert, so entspricht einem ruhenden substantiellen Punkte als Weltlinie eine zur $t\!$ -Achse parallele Gerade, einem gleichförmig bewegten substantiellen Punkte eine gegen die $t\!$ -Achse geneigte Gerade, einem ungleichförmig bewegten substantiellen Punkte eine irgendwie gekrümmte Weltlinie. Fassen wir in einem beliebigen Weltpunkte $x,\,y,\,z,\,t$ die dort durchlaufende Weltlinie auf, und finden wir sie dort parallel mit irgendeinem Radiusvektor $OA'\!$ der vorhin genannten hyperboloidischen Schale, so können wir $OA'\!$ als neue Zeitachse einführen, und bei den damit gegebenen neuen Begriffen von Raum und Zeit erscheint die Substanz in dem betreffenden Weltpunkte als ruhend. Wir wollen nun dieses fundamentale Axiom einführen:

Die in einem beliebigen Weltpunkte vorhandene Substanz kann stets bei geeigneter Festsetzung von Raum und Zeit als ruhend aufgefaßt werden.

Das Axiom bedeutet, daß in jedem Weltpunkte stets der Ausdruck

$c^2dt^2-dx^2-dy^2-dz^2\,$

positiv ausfällt oder, was damit gleichbedeutend ist, daß jede Geschwindigkeit $v\!$ stets kleiner als $c\!$ ausfällt. Es würde danach für alle substantiellen Geschwindigkeiten $c\!$ als obere Grenze bestehen und hierin eben die tiefere Bedeutung der Größe $c\!$ liegen. In dieser anderen Fassung hat das Axiom beim ersten Eindruck etwas Mißfälliges. Es ist aber zu bedenken, daß nun eine modifizierte Mechanik Platz greifen wird, in der die Quadratwurzel aus jener Differentialverbindung zweiten Grades eingeht, so daß Fälle mit Überlichtgeschwindigkeit nur mehr eine Rolle spielen werden, etwa wie in der Geometrie Figuren mit imaginären Koordinaten.

Der Anstoß und wahre Beweggrund für die Annahme der Gruppe $G_c\!$ nun kam daher, daß die Differentialgleichung für die Fortpflanzung von Lichtwellen im leeren Raume jene Gruppe $G_c\!$ besitzt.^[1] Andererseits hat der Begriff starrer Körper nur in einer Mechanik mit der Gruppe $G_\infty\!$ einen Sinn. Hat man nun eine Optik mit $G_c\,,$ und gäbe es andererseits

[6] starre Körper, so ist leicht abzusehen, daß durch die zwei zu $G_c\!$ und zu $G_\infty$ gehörigen hyperboloidischen Schalen eine $t\!$ -Richtung ausgezeichnet sein würde, und das würde weiter die Konsequenz haben, daß man an geeigneten starren optischen Instrumenten im Laboratorium einen Wechsel der Erscheinungen bei verschiedener Orientierung gegen die Fortschreitungsrichtung der Erde müßte wahrnehmen können. Alle auf dieses Ziel gerichteten Bemühungen, insbesondere ein berühmter Interferenzversuch von Michelson, hatten jedoch ein negatives Ergebnis. Um eine Erklärung hierfür zu gewinnen, bildete H. A. Lorentz eine Hypothese, deren Erfolg eben in der Invarianz der Optik für die Gruppe $G_c\!$ liegt. Nach Lorentz soll jeder Körper, der eine Bewegung besitzt, in Richtung der Bewegung eine Verkürzung erfahren haben, und zwar bei einer Geschwindigkeit $v\!$ im Verhältnisse

$1:\sqrt{1-\frac{v^2}{c^2}}.$

Diese Hypothese klingt äußerst phantastisch. Denn die Kontraktion ist nicht etwa als Folge von Widerständen im Äther zu denken, sondern rein als Geschenk von oben, als Begleitumstand des Umstandes der Bewegung.

Ich will nun an unserer Figur zeigen, daß die Lorentzsche Hypothese völlig äquivalent ist mit der neuen Auffassung von Raum und Zeit, wodurch sie viel verständlicher wird. Abstrahieren wir der Einfachheit wegen von $y\!$ und $z\!$ und denken uns eine räumlich eindimensionale Welt, so sind ein wie die $t\!$ -Achse aufrechter und ein gegen die $t\!$ -Achse geneigter Parallelstreifen (siehe Fig. 1) Bilder für den Verlauf eines ruhenden, bezüglich eines gleichförmig bewegten Körpers, der jedesmal eine konstante räumliche Ausdehnung behält. Ist $OA'\!$ parallel dem zweiten Streifen, so können wir $t'\!$ als Zeit und $x'\!$ als Raumkoordinate einführen, und es erscheint dann der zweite Körper als ruhend, der erste als gleichförmig bewegt. Wir nehmen nun an, daß der erste Körper als ruhend aufgefaßt die Länge $l\!$ hat, d. h. der Querschnitt $PP\!$ des ersten Streifens auf der $x\text{-Achse} = l \cdot OC\!$ ist, wo $OC\!$ den Einheitsmaßstab auf der $x\!$ -Achse bedeutet, und daß andererseits der zweite Körper als ruhend aufgefaßt die gleiche Länge $l\!$ hat; letzteres heißt dann, daß der parallel der $x'\!$ -Achse gemessene Querschnitt des zweiten Streifens, $Q'Q'=l \cdot OC'\!$ ist. Wir haben nunmehr in diesen zwei Körpern Bilder von zwei gleichen Lorentzschen Elektronen, einem ruhenden und einem gleichförmig bewegten. Halten wir aber an den ursprünglichen Koordinaten $x,\,t$ fest, so ist als Ausdehnung des zweiten Elektrons der Querschnitt $QQ\!$ seines zugehörigen Streifens parallel der $x\!$ -Achse anzugeben. Nun ist offenbar, da $Q'Q'=l \cdot OC'\!$

[7] ist, $QQ=l \cdot OD'\!$ . Eine leichte Rechnung ergibt, wenn $dx/dt\!$ für den zweiten Streifen $=v\!$ ist, $OD'=OC \cdot \sqrt{1-\frac{v^2}{c^2}}$ , also auch $PP:QQ=1:\sqrt{1-\frac{v^2}{c^2}}\!$ . Dies ist aber der Sinn der Lorentzschen Hypothese von der Kontraktion der Elektronen bei Bewegung. Fassen wir andererseits das zweite Elektron als ruhend auf, adoptieren also das Bezugsystem $x', t'\,,$ so ist als Länge des ersten der Querschnitt $P'P'\!$ seines Streifens parallel $OC'\!$ zu bezeichnen, und wir würden in genau dem nämlichen Verhältnisse das erste Elektron gegen das zweite verkürzt finden; denn es ist in der Figur

$P'P':Q'Q'=OD:OC'=OD':OC=QQ:PP\,.$

Lorentz nannte die Verbindung $t'\!$ von $x\!$ und $t\!$ Ortszeit des gleichförmig bewegten Elektrons und verwandte eine physikalische Konstruktion dieses Begriffs zum besseren Verständnis der Kontraktionshypothese. Jedoch scharf erkannt zu haben, daß die Zeit des einen Elektrons ebenso gut wie die des anderen ist, d. h. daß $t\!$ und $t'\!$ gleich zu behandeln sind, ist erst das Verdienst von A. Einstein.^[2] Damit war nun zunächst die Zeit als ein durch die Erscheinungen eindeutig festgelegter Begriff abgesetzt. An dem Begriffe des Raumes rüttelten weder Einstein noch Lorentz, vielleicht deshalb nicht, weil bei der genannten speziellen Transformation, wo die $x',\,t'\!$ -Ebene sich mit der $x,\,t\!$ -Ebene deckt, eine Deutung möglich ist, als sei die $x\!$ -Achse des Raumes in ihrer Lage erhalten geblieben. Über den Begriff des Raumes in entsprechender Weise hinwegzuschreiten, ist auch wohl nur als Verwegenheit mathematischer Kultur einzutaxieren. Nach diesem zum wahren Verständnis der Gruppe $G_c\!$ jedoch unerläßlichen weiteren Schritt aber scheint mir das Wort Relativitätspostulat für die Forderung einer Invarianz bei der Gruppe $G_c\!$ sehr matt. Indem der Sinn des Postulats wird, daß durch die Erscheinungen nur die in Raum und Zeit vierdimensionale Welt gegeben ist, aber die Projektion in Raum und in Zeit noch mit einer gewissen Freiheit vorgenommen werden kann, möchte ich dieser Behauptung eher den Namen Postulat der absoluten Welt (oder kurz Weltpostulat) geben.

III.
Durch das Weltpostulat wird eine gleichartige Behandlung der vier Bestimmungsstücke $x,\,y,\,z,\,t$ möglich. Dadurch gewinnen, wie ich jetzt

[8] ausführen will, die Formen, unter denen die physikalischen Gesetze sich abspielen, an Verständlichkeit. Vor allem erlangt der Begriff der Beschleunigung ein scharf hervortretendes Gepräge.

Ich werde mich einer geometrischen Ausdrucksweise bedienen, die sich sofort darbietet, indem man im Tripel $x,\,y,\,z$ stillschweigend von $z\!$ abstrahiert. Einen beliebigen Weltpunkt $O\!$ denke ich zum Raum-Zeit-Nullpunkt gemacht. Der Kegel

$c^2t^2-x^2-y^2-z^2=0\,$

Fig. 2

mit $O\!$ als Spitze (Fig. 2) besteht aus zwei Teilen, einem mit Werten $t<0\!$ , einem anderen mit Werten $t>0\!$ . Der erste, der Vorkegel von $O\,,$ besteht, sagen wir, aus allen Weltpunkten, die „Licht nach $O\!$ senden“, der zweite, der Nachkegel von $O\!$ , aus allen Weltpunkten, die „Licht von $O\!$ empfangen“. Das vom Vorkegel allein begrenzte Gebiet mag diesseits von $O\,,$ das vom Nachkegel allein begrenzte jenseits von $O\!$ heißen. Jenseits $O\!$ fällt die schon betrachtete hyperboloidische Schale

$F=c^2t^2-x^2-y^2-z^2=1,\,t>0.$

Das Gebiet zwischen den Kegeln wird erfüllt von den einschaligen hyperboloidischen Gebilden

$-F=x^2+y^2+z^2-c^2t^2=k^2\,$

zu allen konstanten positiven Werten $k^2\,.$ Wichtig sind für uns die Hyperbeln mit $O\!$ als Mittelpunkt, die auf den letzteren Gebilden liegen. Die einzelnen Äste dieser Hyperbeln mögen kurz die Zwischenhyperbeln zum Zentrum $O\!$ heißen. Ein solcher Hyperbelast würde, als Weltlinie eines substantiellen Punktes gedacht, eine Bewegung repräsentieren, die für $t=-\infty\!$ und $t=+\infty\!$ asymptotisch auf die Lichtgeschwindigkeit $c\!$ ansteigt.

Nennen wir in Analogie zum Vektorbegriff im Raume jetzt eine gerichtete Strecke in der Mannigfaltigkeit der $x,\,y,\,z,\,t$ einen Vektor, so haben wir zu unterscheiden zwischen den zeitartigen Vektoren mit Richtungen von $O\!$ nach der Schale $+F=1,\,t>0\!$ und den raumartigen Vektoren mit Richtungen von $O\!$ nach $-F=1\!$ . Die Zeitachse kann jedem Vektor der ersten Art parallel laufen. Ein jeder Weltpunkt zwischen Vorkegel und Nachkegel von $O\!$ kann durch das Bezugsystem als gleichzeitig mit $O\,,$ aber ebensogut auch als früher als $O\!$ oder als später als $O\!$ eingerichtet werden. Jeder Weltpunkt diesseits $O\!$ ist notwendig

[9] stets früher, jeder Weltpunkt jenseits $O\!$ notwendig stets später als $O\,.$ Dem Grenzübergang zu $c=\infty\!$ würde ein völliges Zusammenklappen des keilförmigen Einschnittes zwischen den Kegeln in die ebene Mannigfaltigkeit $t=0\!$ entsprechen. In den gezeichneten Figuren ist dieser Einschnitt absichtlich mit verschiedener Breite angelegt.

Einen beliebigen Vektor wie von $O\!$ nach $x,\,y,\,z,\,t$ zerlegen wir in die vier Komponenten $x,\,y,\,z,\,t\,.$ Sind die Richtungen zweier Vektoren beziehungsweise die eines Radiusvektors $OR\!$ von $O\!$ an eine der Flächen $\mp F=1\!$ und dazu einer Tangente $RS\!$ im Punkte $R\!$ der betreffenden Fläche, so sollen die Vektoren normal zueinander heißen. Danach ist

$c^2t\,t_1-x\,x_1-y\,y_1-z\,z_1=0\!$

die Bedingung dafür, daß die Vektoren mit den Komponenten $x,\,y,\,z,\,t$ und $x_1,\,y_1,\,z_1,\,t_1$ normal zueinander sind.

Für die Beträge von Vektoren der verschiedenen Richtungen sollen die Einheitsmaßstäbe dadurch fixiert sein, daß einem raumartigen Vektor von $O\!$ nach $-F=1\!$ stets der Betrag 1, einem zeitartigen Vektor von $O\!$ nach $+F=1,\,t>0$ stets der Betrag $1/c\!$ zugeschrieben wird.

Denken wir uns nun in einem Weltpunkte $P(x,\,y,\,z,\,t)$ die dort durchlaufende Weltlinie eines substantiellen Punktes, so entspricht danach dem zeitartigen Vektorelement $dx,\,dy,\,dz,\,dt$ im Fortgang der Linie der Betrag

$d \tau =\frac{1}{c}\sqrt{c^2dt^2-dx^2-dy^2-dz^2}.$

Das Integral $\int d\tau =\tau$ dieses Betrages auf der Weltlinie von irgendeinem fixierten Ausgangspunkte $P_0\!$ bis zu dem variablen Endpunkte $P\!$ geführt, nennen wir die Eigenzeit des substantiellen Punktes in $P\,.$ Auf der Weltlinie betrachten wir $x,\,y,\,z,\,t\,,$ d. s. die Komponenten des Vektors $OP\,,$ als Funktionen der Eigenzeit $\tau\,,$ bezeichnen deren erste Differentialquotienten nach $\tau\!$ mit $\dot x,\,\dot y,\,\dot z,\,\dot t\,,$ deren zweite Differentialquotienten nach $\tau\!$ mit $\ddot x,\,\ddot y,\,\ddot z,\,\ddot t$ und nennen die zugehörigen Vektoren, die Ableitung des Vektors $OP\!$ nach $\tau\!$ den Bewegungsvektor in $P\!$ und die Ableitung dieses Bewegungsvektors nach $\tau\!$ den Beschleunigungsvektor in $P\,.$ Dabei gilt

$c^2\dot t^2- \dot x^2 -\dot y^2 -\dot z^2 = c^2,$

$c^2\dot t\, \ddot t- \dot x\, \ddot x -\dot y\, \ddot y -\dot z\, \ddot z = 0,$

d. h. der Bewegungsvektor ist der zeitartige Vektor in Richtung der Weltlinie in $P\!$ vom Betrage 1, und der Beschleunigungsvektor in $P\!$ ist normal zum Bewegungsvektor in $P\,,$ also jedenfalls ein raumartiger Vektor.

[10] Nun gibt es, wie man leicht einsieht, einen bestimmten Hyperbelast, der mit der Weltlinie in $P\!$ drei unendlich benachbarte Punkte gemein hat, und dessen Asymptoten Erzeugende eines Vorkegels und eines Nachkegels sind (siehe unten Fig. 3). Dieser Hyperbelast heiße die Krümmungshyperbel in $P\,.$ Ist $M\!$ das Zentrum dieser Hyperbel, so handelt es sich also hier um eine Zwischenhyperbel zum Zentrum $M\,.$ Es sei $\varrho\!$ der Betrag des Vektors 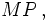$MP\,,$ so erkennen wir den Beschleunigungsvektor in $P\!$ als den Vektor in Richtung $MP\!$ vom Betrage $c^2/\varrho.$

Sind $\ddot x,\,\ddot y,\,\ddot z,\,\ddot t$ sämtlich Null, so reduziert sich die Krümmungshyperbel auf die in $P\!$ die Weltlinie berührende Gerade, und es ist $\varrho=\infty\!$ zu setzen.

IV.
Um darzutun, daß die Annahme der Gruppe $G_c\!$ für die physikalischen Gesetze nirgends zu einem Widerspruche führt, ist es unumgänglich, eine Revision der gesamten Physik auf Grund der Voraussetzung dieser Gruppe vorzunehmen. Diese Revision ist bereits in einem gewissen Umfange erfolgreich geleistet für Fragen der Thermodynamik und Wärmestrahlung^[3], für die elektromagnetischen Vorgänge, endlich für die Mechanik unter Aufrechterhaltung des Massenbegriffs.^[4]

Für letzteres Gebiet ist vor allem die Frage aufzuwerfen: Wenn eine Kraft mit den Komponenten $X,\,Y,\,Z$ nach den Raumachsen in einem Weltpunkte $P(x,\,y,\,z,\,t)$ angreift, wo der Bewegungsvektor $\dot x,\,\dot y,\,\dot z,\,\dot t$ ist, als welche Kraft ist diese Kraft bei einer beliebigen Änderung des Bezugsystemes aufzufassen? Nun existieren gewisse erprobte Ansätze über die ponderomotorische Kraft im elektromagnetischen Felde in den Fällen, wo die Gruppe $G_c\!$ unzweifelhaft zuzulassen ist. Diese Ansätze führen zu der einfachen Regel: Bei Änderung des Bezugsystemes ist die vorausgesetzte Kraft derart als Kraft in den neuen Raumkoordinaten anzusetzen, daß dabei der zugehörige Vektor mit den Komponenten

$\dot t X,\, \dot t Y,\, \dot t Z,\, \dot t T,$

$T=\frac{1}{c^2}\left( \frac{\dot x}{\dot t}X + \frac{\dot y}{\dot t} Y + \frac{\dot z}{\dot t}Z\right)$

die durch $c^2\!$ dividierte Arbeitsleistung der Kraft im Weltpunkte ist, sich unverändert erhält. Dieser Vektor ist stets normal zum Bewegungsvektor in $P\!$ . Ein solcher, zu einer Kraft in $P\!$ gehörender Kraftvektor soll ein bewegender Kraftvektor in $P\!$ heißen.

[11] Nun werde die durch $P\!$ laufende Weltlinie von einem substantiellen Punkte mit konstanter mechanischer Masse $m\!$ beschrieben. Das $m\!$ -fache des Bewegungsvektors in $P\!$ heiße der Impulsvektor in $P\,,$ das $m\!$ -fache des Beschleunigungsvektors in $P\!$ der Kraftvektor der Bewegung in $P\,.$ Nach diesen Definitionen lautet das Gesetz dafür, wie die Bewegung eines Massenpunktes bei gegebenem bewegenden Kraftvektor statthat:^[5]

Der Kraftvektor der Bewegung ist gleich dem bewegenden Kraftvektor.

Diese Aussage faßt vier Gleichungen für die Komponenten nach den vier Achsen zusammen, wobei die vierte, weil von vornherein beide genannten Vektoren normal zum Bewegungsvektor sind, sich als eine Folge der drei ersten ansehen läßt. Nach der obigen Bedeutung von $T\!$ stellt die vierte zweifellos den Energiesatz dar. Als kinetische Energie des Massenpunktes ist daher das $c^2\!$ -fache der Komponente des Impulsvektors nach der $t\!$ -Achse zu definieren. Der Ausdruck hierfür ist

$m\,c^2 \frac{dt}{d\tau}=m\,c^2 \left/ \sqrt{1-\frac{v^2}{c^2}},\right.$

d. i. nach Abzug der additiven Konstante $m\,c^2\!$ der Ausdruck $\tfrac{1}{2}m\,v^2$ der Newtonschen Mechanik bis auf Größen von der Ordnung $1/c^2\,.$ Sehr anschaulich erscheint hierbei die Abhängigkeit der Energie vom Bezugsysteme. Da nun aber die $t\!$ -Achse in die Richtung jedes zeitartigen Vektors gelegt werden kann, so enthält andererseits der Energiesatz, für jedes mögliche Bezugsystem gebildet, bereits das ganze System der Bewegungsgleichungen. Diese Tatsache behält bei dem erörterten Grenzübergang zu $c=\infty\!$ ihre Bedeutung auch für den axiomatischen Aufbau der Newtonschen Mechanik und ist in solchem Sinne hier bereits von Herrn J. R. Schütz^[6] wahrgenommen worden.

Man kann von vornherein das Verhältnis von Längeneinheit und Zeiteinheit derart wählen, daß die natürliche Geschwindigkeitsschranke $c=1\!$ wird. Führt man dann noch $\sqrt{-1}\cdot t=s$ an Stelle von $t\!$ ein, so wird der quadratische Differentialausdruck

$d\tau^2=-dx^2-dy^2-dz^2-ds^2,\,$

also völlig symmetrisch in $x,\,y,\,z,\,s\,,$ und diese Symmetrie überträgt sich auf ein jedes Gesetz, das dem Weltpostulate nicht widerspricht. Man kann danach das Wesen dieses Postulates mathematisch sehr prägnant in die mystische Formel kleiden:

$3.10^5\, \text{km}=\sqrt{-1}\,\text{sek.}$

[12]

V.

Die durch das Weltpostulat geschaffenen Vorteile werden vielleicht durch nichts so schlagend belegt wie durch Angabe der von einer

Fig. 3. Fig. 4.

beliebig bewegten punktförmigen Ladung nach der Maxwell-Lorentzschen Theorie ausgehenden Wirkungen. Denken wir uns die Weltlinie eines solchen punktförmigen Elektrons mit der Ladung $e\!$ und führen auf ihr die Eigenzeit $\tau\!$ ein von irgendeinem Anfangspunkte aus. Um das vom Elektron in einem beliebigen Weltpunkte $P_1\!$ veranlaßte Feld zu haben, konstruieren wir den zu $P_1\!$ gehörigen Vorkegel (Fig. 4). Dieser trifft die unbegrenzte Weltlinie des Elektrons, weil deren Richtungen überall die von zeitartigen Vektoren sind, offenbar in einem einzigen Punkte $P\,.$ Wir legen in $P\!$ an die Weltlinie die Tangente und konstruieren durch $P_1\!$ die Normale $P_1Q\!$ auf diese Tangente. Der Betrag von $P_1Q\!$ sei $r\,.$ Als der Betrag von $PQ\!$ ist dann gemäß der Definition eines Vorkegels $r/c\!$ zu rechnen. Nun stellt der Vektor in Richtung $PQ\!$ vom Betrage $e/r\!$ in seinen Komponenten nach den $x-,\,y-,\,z-\!$ Achsen das mit $c\!$ multiplizierte Vektorpotential, in der Komponente nach der $t\!$ -Achse das skalare Potential des von $e\!$ erregten Feldes für den Weltpunkt $P_1\!$ vor. Hierin liegen die von A. Liénard und von E. Wiechert aufgestellten Elementargesetze.^[7]
Bei der Beschreibung des vom Elektron hervorgerufenen Feldes selbst tritt sodann hervor, daß die Scheidung des Feldes in elektrische und magnetische Kraft eine relative ist mit Rücksicht auf die zugrunde gelegte Zeitachse; am übersichtlichsten sind beide Kräfte zusammen zu beschreiben in einer gewissen, wenn auch nicht völligen Analogie zu einer Kraftschraube der Mechanik.

Ich will jetzt die von einer beliebig bewegten punktförmigen Ladung auf eine andere beliebig bewegte punktförmige Ladung ausgeübte ponderomotorische Wirkung beschreiben. Denken wir uns durch den Weltpunkt

[13] $P_1\!$ die Weltlinie eines zweiten punktförmigen Elektrons von der Ladung $e_1\!$ führend. Wir bestimmen $P,\,Q,\,r\!$ wie vorhin, konstruieren sodann (Fig. 4) den Mittelpunkt der Krümmungshyperbel in $P\,,$ endlich die Normale $MN\!$ von $M\!$ aus auf eine durch $P\!$ parallel zu $QP_1\!$ gedachte Gerade. Wir legen nun, mit $P\!$ als Anfangspunkt, ein Bezugsystem folgendermaßen fest, die $t\!$ -Achse in die Richtung $PQ\,,$ die $x\!$ -Achse in die Richtung $QP_1\,,$ die $y\!$ -Achse in die Richtung $MN\,,$ womit schließlich auch die Richtung der $z\!$ -Achse als normal zu den $t-,\,x-,\,y-\!$ Achsen bestimmt ist. Der Beschleunigungsvektor in $P\!$ sei $\ddot x,\,\ddot y,\,\ddot z,\,\ddot t,$ der Bewegungsvektor in $P_1\!$ sei $\dot x_1,\,\dot y_1,\,\dot z_1,\,\dot t_1.$ Jetzt lautet der von dem ersten beliebig bewegten Elektron $e\!$ auf das zweite beliebig bewegte Elektron $e_1\!$ in $P_1\!$ ausgeübte bewegende Kraftvektor:

$-e\,e_1 \left( \dot t_1 - \frac{\dot x_1}{c} \right) \mathfrak{K}\,,$

wobei für die Komponenten $\mathfrak{K}_x,\,\mathfrak{K}_y,\,\mathfrak{K}_z,\,\mathfrak{K}_t$ des Vektors $\mathfrak{K}$ die drei Relationen bestehen:

$c\,\mathfrak{K}_t - \mathfrak{K}_x = \frac{1}{r^2}, \quad \mathfrak{K}_y=\frac{\ddot y}{c^2 r}, \quad \mathfrak{K}_z=0$

und viertens dieser Vektor $\mathfrak{K}\,$ normal zum Bewegungsvektor in $P_1\!$ ist und durch diesen Umstand allein in Abhängigkeit von dem letzteren Bewegungsvektor steht.

Vergleicht man mit dieser Aussage die bisherigen Formulierungen^[8] des nämlichen Elementargesetzes über die ponderomotorische Wirkung bewegter punktförmiger Ladungen aufeinander, so wird man nicht umhin können, zuzugeben, daß die hier in Betracht kommenden Verhältnisse ihr inneres Wesen voller Einfachheit erst in vier Dimensionen enthüllen, auf einen von vornherein aufgezwungenen dreidimensionalen Raum aber nur eine sehr verwickelte Projektion werfen.

In der dem Weltpostulate gemäß reformierten Mechanik fallen die Disharmonien, die zwischen der Newtonschen Mechanik und der modernen Elektrodynamik gestört haben, von selbst aus. Ich will noch die Stellung des Newtonschen Attraktionsgesetzes zu diesem Postulate berühren. Ich will annnehmen, wenn zwei Massenpunkte $m,\,m_1\!$ ihre Weltlinien beschreiben, werde von $m\!$ auf $m_1\!$ ein bewegender Kraftvektor ausgeübt genau von dem soeben im Falle von Elektronen angegebenen Ausdruck, nur daß statt $-e\,e_1\!$ jetzt $+m\,m_1\!$ treten soll. Wir betrachten nun speziell den Fall, daß der Beschleunigungsvektor von $m\!$ konstant Null ist, wobei wir dann $t\!$ so einführen mögen, daß $m\!$ als ruhend aufzufassen ist, und es erfolge die Bewegung von $m_1\!$

[14] allein mit jenem von $m\!$ herrührenden bewegenden Kraftvektor. Modifizieren wir nun diesen angegebenen Vektor zunächst durch Hinzusetzen des Faktors $\dot{t}^{-1}=\sqrt{1-\frac{v^2}{c^2}},$ der bis auf Größen von der Ordnung $1/c^2\!$ auf 1 hinauskommt, so zeigt sich^[9], daß für die Orte $x_1,\,y_1,\,z_1$ von $m_1\!$ und ihren zeitlichen Verlauf genau wieder die Keplerschen Gesetze hervorgehen würden, nur daß dabei an Stelle der Zeiten $t_1\!$ die Eigenzeiten $\tau_1\!$ von $m_1\!$ eintreten würden. Auf Grund dieser einfachen Bemerkung läßt sich dann einsehen, daß das vorgeschlagene Anziehungsgesetz verknüpft mit der neuen Mechanik nicht weniger gut geeignet ist, die astronomischen Beobachtungen zu erklären als das Newtonsche Anziehungsgesetz verknüpft mit der Newtonschen Mechanik.

Auch die Grundgleichungen für die elektromagnetischen Vorgänge in ponderablen Körpern fügen sich durchaus dem Weltpostulate. Sogar die von Lorentz gelehrte Ableitung dieser Gleichungen auf Grund von Vorstellungen der Elektronentheorie braucht zu dem Ende keineswegs verlassen zu werden, wie ich anderwärts zeigen werde.

Die ausnahmslose Gültigkeit des Weltpostulates ist, so möchte ich glauben, der wahre Kern eines elektromagnetischen Weltbildes, der von Lorentz getroffen, von Einstein weiter herausgeschält, nachgerade vollends am Tage liegt. Bei der Fortbildung der mathematischen Konsequenzen werden genug Hinweise auf experimentelle Verifikationen des Postulates sich einfinden, um auch diejenigen, denen ein Aufgeben altgewohnter Anschauungen unsympathisch oder schmerzlich ist, durch den Gedanken an eine prästabilierte Harmonie zwischen der reinen Mathematik und der Physik auszusöhnen.

Verlag von B. G. Teubner in Leipzig und Berlin.

H. Minkowski:

Geometrie der Zahlen

In 2 Lieferungen.

I. Lieferung. [240 S.] gr. 8. 1896. Geh. n. M. 8.—

Diese Schrift enthält eine neue Art Anwendungen der Analysis des Unendlichen auf die Zahlentheorie oder, besser gesagt, knüpft ein neues Band zwischen diesen beiden Gebieten. Es werden hier in bezug auf eine Klasse von vielfachen Integralen einige Ungleichheiten entwickelt, die eine fundamentale Bedeutung haben für Fragen über approximative Lösungen von Gleichungen durch rationale Zahlen und für Probleme, welche mit derartigen Fragen zusammenhängen. Im Mittelpunkt der Untersuchung steht ein arithmetisches Prinzip von besonderer Fruchtbarkeit, dessen vielseitige Verwendung auf der Mannigfaltigkeit von Einzelgestalten beruht, die eine nirgends konkave Fläche mit Mittelpunkt darzubieten imstande ist. Das erste Kapitel enthält eine eingehende Begründung der Eigenschaften der nirgends konkaven Flächen. Im zweiten sind einige hier zu verwendende bekannte Sätze aus der Funktionentheorie mit ihren Beweisen dargestellt. Das dritte Kapitel ist der Entwicklung des genannten Prinzips gewidmet. Das vierte bis siebente Kapitel bringt Anwendungen des Prinzips auf die approximative Auflösung von Gleichungen durch rationale Zahlen und durch ganze Zahlen, auf die Theorie der algebraischen Zahlen, auf die Theorie der quadratischen Formen usw., das achte Kapitel endlich eine besondere Untersuchung, die mit jenem Prinzip in loserem Zusammenhange steht. Geometrie der Zahlen ist das Buch betitelt, weil der Verf. zu den Methoden, die die in ihm gegebenen arithmetischen Sätze liefern, durch räumliche Anschauung geführt worden ist.

Die vorliegende erste Lieferung enthält bereits die meisten allgemeinen Theoreme, während die in Vorbereitung befindliche Schlußlieferung noch mancherlei Anwendungen bringen wird.

↑ Eine wesentliche Anwendung dieser Tatsache findet sich bereits bei W. Voigt, Göttinger Nachr. 1887, p. 41.

↑ A. Einstein, Ann. d. Phys. 17, 1905, p. 891; Jahrb. d. Radioaktivität u. Elektronik 4, 1907, p. 411.

↑ M. Planck, Zur Dynamik bewegter Systeme, Berliner Ber. 1907, p. 542 (auch Ann. d. Phys. 26, 1908, p. 1).

↑ H. Minkowski, Die Grundgleichungen für die elektromagnetischen Vorgänge in bewegten Körpern, Göttinger Nachr. 1908, p. 53.

↑ H. Minkowski, a. a. 0. p. 107. — Vgl. auch M. Planck, Verh. d. Physik. Ges. 4, p. 136, 1906.

↑ J. R. Schütz, Das Prinzip der absoluten Erhaltung der Energie. Göttinger Nachr. 1897, p. 110.

↑ A. Liénard, Champ électrique et magnétique produit par une charge concentrie en un point et animée d’un mouvement quelconque, L’Éclairage électrique 16 (1898), p. 5, 53, 106; Wiechert, Elektrodynamische Elementargesetze, Arch. néerl. (2), 5 (1900), p. 549.

↑ K. Schwarzschild, Göttinger Nachr. 1903, p. 132. — H. A. Lorentz, Enzykl. d. math. Wissensch., Art. V, 14, p. 199.

↑ H. Minkowski, a. a. 0., p. 110.

＿＿＿＿

Vorwort.
Der Vortrag über „Raum und Zeit“, den Hermann Minkowski auf der Versammlung Deutscher Naturforscher und Ärzte zu Köln gehalten hat, bildet die letzte seiner genialen Schöpfungen. Leider ist es ihm nicht beschieden gewesen, den feineren Ausbau seines kühnen Entwurfs einer Mechanik, in welcher die Zeit den drei Dimensionen des Raumes koordiniert ist, zu vollenden. Denn ein tragisches Geschick hat den als Mensch und Forscher gleich geschätzten Verfasser auf der Höhe seines Lebens und Schaffens am 12. Januar d. J. der Wissenschaft, seinen Lieben und Freunden jäh entrissen.

Das verständnisvolle und begeisterte Interesse, das sein Vortrag erweckt hatte, erfüllte Minkowski mit innerer Befriedigung, und er wünschte, seine Darlegungen durch eine Sonderausgabe weiteren Kreisen zugänglich zu machen. Der Verlagsbuchhandlung von B. G. Teubner und dem Unterzeichneten ist es eine schmerzliche Pflicht der Pietät und Freundschaft, diesen letzten Wunsch des Verstorbenen hiermit zu erfüllen.

Halle a. S., den 20. Februar 1909.

A. Gutzmer.

NAMs出版プロジェクト

月曜日, 1月 30, 2012

Karinthy Frigyes　Lancszemek　フリジェシュ・カリンティ「鎖」1929

日曜日, 1月 29, 2012

Raum und Zeit (Minkowski) 1908

Links

Previous Posts

Archives

NAMs出版プロジェクト

月曜日, 1月 30, 2012

Karinthy Frigyes Lancszemek フリジェシュ・カリンティ「鎖」1929

日曜日, 1月 29, 2012

Raum und Zeit (Minkowski) 1908

Links

Previous Posts

Archives

Karinthy Frigyes　Lancszemek　フリジェシュ・カリンティ「鎖」1929