晩年のパーソンズによるルーマン批判 : 関本洋司のブログより
http://yojiseki.exblog.jp/6653410/晩年のパーソンズによるルーマン批判 |
タルコット・パーソンズはその実質的最終講議で、レベルの違うものを混同しているとして、かつて自らの弟子だったニコラス・ルーマンを批判している。普通ならルーマンは変数が多すぎると批判すると思うが、パーソンズの晩年のカントへの傾倒も宜なるかなと思わせる批判である。
以下引用です。
<ここ数日、私は『社会科学における一般理論の探究』(Explorations in General Theory in Social Science)という論文集の中の非常に興味のある論文を繰返し読んでいます。それはドイツの社会学者ルーマン(N・Luhmann)という人の論文です。彼の業績は、近年、多くの人々の注目を集めていますので、業績は知らなくても、彼の名前は皆様のうち何人かは御承知のことと思います。さてルーマンは、交換の一般化された媒体に接近する問題を取り上げようと試みています。ここ数日間、これを読み返しながら、私はルーマンが行為の一般理論の異なったサブシステムの区分に失敗しているため、彼の説明には重大な困難がひそんでいると確信するように成りました。例えば、彼は一般化されたメディアの分類をしていますので、私は次の時間に、それについていくつかのことを述べるつもりですが、そのなかでも「貨幣」、「権力」等についてはすでに御存知のことと思います。彼はこれに属するものとして貨幣と権力を認めていますが、協同者と私が用いて来た他の二つのカテゴリーー「影響力」と「価値委託」ーの代わりに、彼は「愛」(love)と「真実」(truth)(図)を用います。

ところで、他にもいろいろ難点がありますが、重要なことは、「愛」と「真実」は、一般行為システムのレベルに属するとしても、「貨幣」と「権力」は一般行為システムのレベルではなくて、社会システムに属しているというふうに思われます。私が考えていることを簡単に説明するに当ってまず述べたいことは、そこで言及しているシステムが何であるかを注意深く確認することの重要性であります。ルーマンはすべてのことを社会システムとして処理しており、文化システムを社会システムとは別個なものとして論じていません。>
(T・パーソンズ『社会システムの構造と変化』1984年、創文社p.34より)
参考:
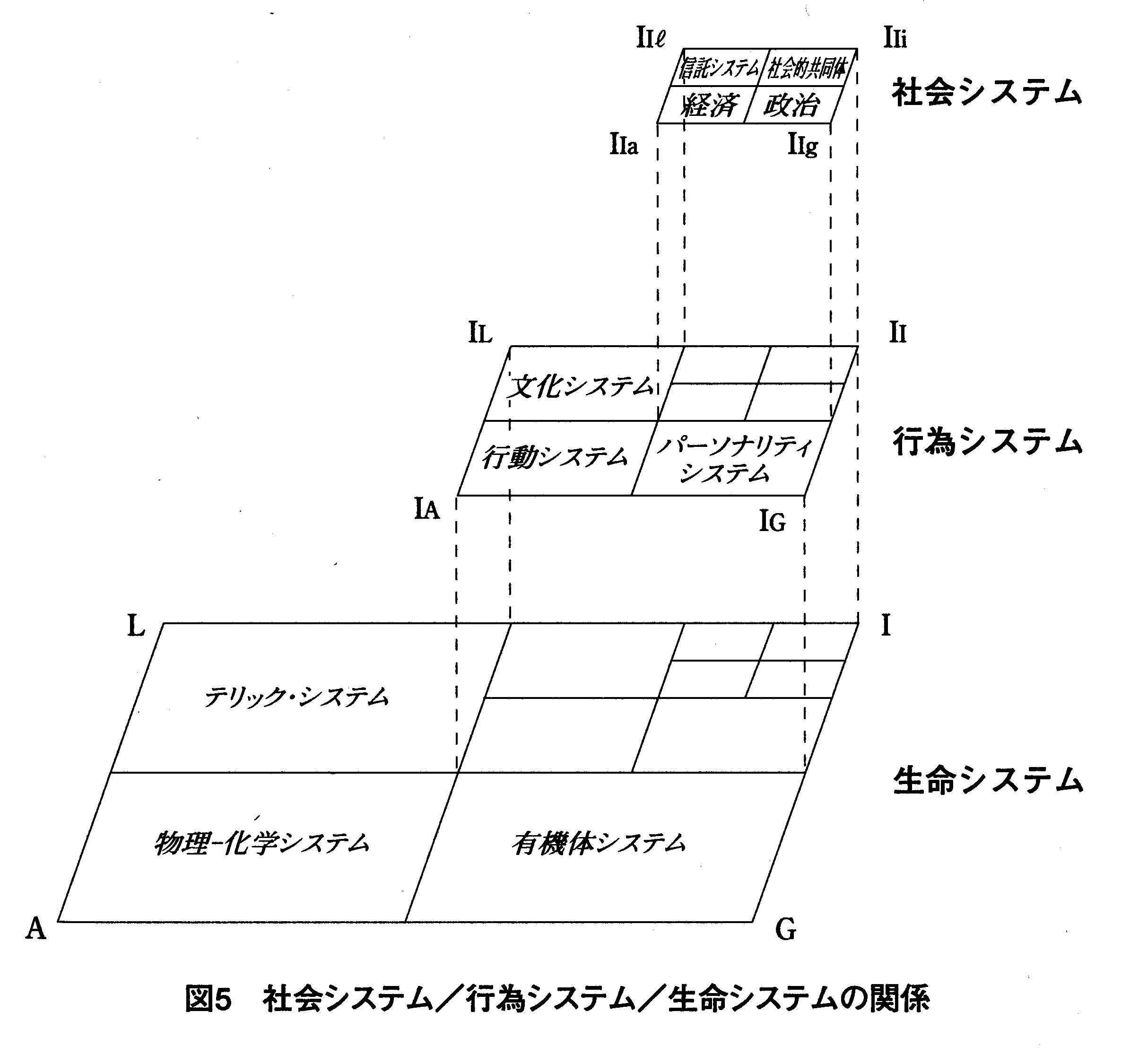
やはり以前にも紹介した以下の図を参照するとわかりやすいかも知れない。
『人間の条件パラダイム—行為理論と人間の条件第四部 』(p264)富永健一作製の図↓
(AGILではなくLIGA図式になっている。)
追記:
先日書いたエルニーニョに関する記事↓と照らし合わせると生命システムの位置づけには実感としてうなづける。
http://yojiseki.exblog.jp/d2008-01-06
追記の追記:
パーソンズのシステム図は、インド生まれの思想家、サティシュ・クマールの以下の説と響き合う。
以下、ナマケモノ倶楽部MLより。
http://shop.slowbusiness.org/index.php?main_page=product_info&cPath=87_92_115&products_id=505
●つながりを取りもどす時代へ 持続可能な社会をめざす環境思想
http://shop.slowbusiness.org/index.php?main_page=product_info&cPath=87_92_118&products_id=556
■3つの“S”
――Soil(土)、Soul(心)、Society(社会)
エコロジーとは何か。土と心と社会という3つの言葉で説明できます。一体であるはずのこの3つが、バラバラだとどうなるでしょう?
例えば、社会運動家たちはこう考えるかもしれない。「環境どころじゃない。社会にまず正義を実現しなければ」と。また、環境運動家たちはこう言うかもしれない。「木や森、山に川、海や動物たちがあっての人間だ。人間だけの平和には興味がない」と。
さらに、自己啓発やスピリチュアルな世界、宗教などに救いを求める人たちは言うかもしれない。「地球は放っておいても大丈夫。必要なのは自己の成長と発展だけだ。自分が幸せなら、おのずと平和はついてくる」と。
新しい世界を目指す運動が、バラバラでは困るでしょう。それらを結びつける必要があります。なぜなら、これら3つの運動はどれも、ホリスティックで持続可能な世界を目指しているのだから。同様に、土と心と社会は、一体で切り離すことができません。
以下引用です。
<ここ数日、私は『社会科学における一般理論の探究』(Explorations in General Theory in Social Science)という論文集の中の非常に興味のある論文を繰返し読んでいます。それはドイツの社会学者ルーマン(N・Luhmann)という人の論文です。彼の業績は、近年、多くの人々の注目を集めていますので、業績は知らなくても、彼の名前は皆様のうち何人かは御承知のことと思います。さてルーマンは、交換の一般化された媒体に接近する問題を取り上げようと試みています。ここ数日間、これを読み返しながら、私はルーマンが行為の一般理論の異なったサブシステムの区分に失敗しているため、彼の説明には重大な困難がひそんでいると確信するように成りました。例えば、彼は一般化されたメディアの分類をしていますので、私は次の時間に、それについていくつかのことを述べるつもりですが、そのなかでも「貨幣」、「権力」等についてはすでに御存知のことと思います。彼はこれに属するものとして貨幣と権力を認めていますが、協同者と私が用いて来た他の二つのカテゴリーー「影響力」と「価値委託」ーの代わりに、彼は「愛」(love)と「真実」(truth)(図)を用います。

ところで、他にもいろいろ難点がありますが、重要なことは、「愛」と「真実」は、一般行為システムのレベルに属するとしても、「貨幣」と「権力」は一般行為システムのレベルではなくて、社会システムに属しているというふうに思われます。私が考えていることを簡単に説明するに当ってまず述べたいことは、そこで言及しているシステムが何であるかを注意深く確認することの重要性であります。ルーマンはすべてのことを社会システムとして処理しており、文化システムを社会システムとは別個なものとして論じていません。>
(T・パーソンズ『社会システムの構造と変化』1984年、創文社p.34より)
参考:
やはり以前にも紹介した以下の図を参照するとわかりやすいかも知れない。
『人間の条件パラダイム—行為理論と人間の条件第四部 』(p264)富永健一作製の図↓
(AGILではなくLIGA図式になっている。)

追記:
先日書いたエルニーニョに関する記事↓と照らし合わせると生命システムの位置づけには実感としてうなづける。
http://yojiseki.exblog.jp/d2008-01-06
追記の追記:
パーソンズのシステム図は、インド生まれの思想家、サティシュ・クマールの以下の説と響き合う。
以下、ナマケモノ倶楽部MLより。
http://shop.slowbusiness.org/index.php?main_page=product_info&cPath=87_92_115&products_id=505
●つながりを取りもどす時代へ 持続可能な社会をめざす環境思想
http://shop.slowbusiness.org/index.php?main_page=product_info&cPath=87_92_118&products_id=556
■3つの“S”
――Soil(土)、Soul(心)、Society(社会)
エコロジーとは何か。土と心と社会という3つの言葉で説明できます。一体であるはずのこの3つが、バラバラだとどうなるでしょう?
例えば、社会運動家たちはこう考えるかもしれない。「環境どころじゃない。社会にまず正義を実現しなければ」と。また、環境運動家たちはこう言うかもしれない。「木や森、山に川、海や動物たちがあっての人間だ。人間だけの平和には興味がない」と。
さらに、自己啓発やスピリチュアルな世界、宗教などに救いを求める人たちは言うかもしれない。「地球は放っておいても大丈夫。必要なのは自己の成長と発展だけだ。自分が幸せなら、おのずと平和はついてくる」と。
新しい世界を目指す運動が、バラバラでは困るでしょう。それらを結びつける必要があります。なぜなら、これら3つの運動はどれも、ホリスティックで持続可能な世界を目指しているのだから。同様に、土と心と社会は、一体で切り離すことができません。





![f^{-1}((a,\infty]) \in M](https://upload.wikimedia.org/math/4/f/1/4f14a90c04dffbcdedab840b418b2e01.png)

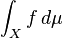
 の積分を
の積分を
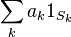


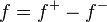


![\int_{[0,1]} 1_{\mathbf{Q}} \, d \mu = \mu(\mathbf{Q} \cap [0,1]) = 0](https://upload.wikimedia.org/math/7/6/5/765bbdb3ee46ca29e0b5b6eaf3b596ce.png)







 .
. .
.





