火曜日, 4月 30, 2019

Debunking Economics [経済学の正体を暴く]Steve Keen (著)2nd Edition 2012



投資意欲が穏健ではなく過大：(can we avoid…)

：雇用率~~、負債率↗︎。（これに賃金率=所得シェア？が加われば立体視され得る。後述）

http://www.debtdeflation.com/blogs/wp-content/uploads/books/Keen_supplement.pdf :

労働者、資本家、銀行家の所得シェア。（大平穏→格差拡大）：



Debunking Economics [経済学の正体を暴く]Steve Keen (著)2nd Edition 2012
https://nam-students.blogspot.com/2019/04/debunking-economics-steve-keen-2nd.html@

ちなみにキーン・モデルの3変数は、
雇用率(Employment)、
産出[=GDP]に占める賃金の割合(Wage Share)、
民間負債の対GDP比率(Bank Share[=主流派が軽視したミンスキー的認識])だ。
(それぞれx,y,z)
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgatun8YpK9WlP2CxnT3TFPi-MTPv8hXbsjAnW5eA7jHbgCjvvp3jIw3l_vFpDfRHBIXOAwka03DSsQqVuZzYaXh2hB_zWNIkyYFheabTZE4LkdR_54S86W_nELBPDgE3FaZNoE/s1600/IMG_4653.PNG
3変数が相互に影響し合うから7つの変数を使うDSGEモデルより複雑になる。
循環、危機、格差の拡大、大平穏(凪)というDSGEでは説明できなかった４つの事象を表出する(『次なる金融危機』39頁)。

『経済学の正体を暴く』(未邦訳)より、1995年ミンスキー・モデルにおける負債の渦巻き状図：

危機↖︎

銀行家＼　(両者trade-off)
労働者　　


結論を言えば労働者たちが自分たちの銀行を持たなければならない。
Bank Share は銀行家の所得ではなく、民間の負債率のはず…

Debunking Economics: The Naked Emperor Dethroned? (English Edition) [経済学の正体を暴く]2nd Edition 2012, Kindle版

Steve Keen (著)

CONTENTS  

Tables, figures and boxes

 Where are the diagrams? 

Preface to the second edition 

Preface to the first edition 

1 Predicting the ‘unpredictable’ 

2 No more Mr Nice Guy 

Part 1 Foundations: the logical flaws in the key concepts of conventional economics

 3 The calculus of hedonism 

4 Size does matter 

5 The price of everything and the value of nothing 

6 To each according to his contribution 

Part 2 Complexities: issues omitted from standard courses that should be part of an education in economics

 7 The holy war over capital

8 There is madness in their method 

9 Let’s do the Time Warp again 

10 Why they didn’t see it coming 

11 The price is not right 

12 Misunderstanding the Great Depression and the Great Recession 

Part 3 Alternatives: different ways to think about economics 

13 Why I did see ‘It’ coming 

14 A monetary model of capitalism 

15 Why stock markets crash 

16 Don’t shoot me, I’m only the piano 

17 Nothing to lose but their minds 

18 There are alternatives Bibliography

 Index

内容
テーブル、図、箱
 図はどこにありますか。
第2版​​のはじめに
初版のはじめに
1「予測不可能」を予測する
2これ以上氏ナイスガイ
パート1基礎：従来型経済学の重要概念における論理的欠陥
 3快楽主義の計算
4サイズは関係ありません5すべての価格と価値なし
6それぞれに彼の貢献に従って
パート2複雑さ：経済学の教育の一部であるべき標準的なコースから省略された問題
 7資本に対する聖戦
8彼らの方法には狂気がある
9もう一度タイムワープをやりましょう
10なぜ彼らはそれが来るのを見なかったのか
11価格が正しくありません
12大恐慌と大後退の誤解
第3部代替案：経済学について考えるさまざまな方法
13それがやってくるのを見たのはなぜですか
14資本主義の貨幣モデル
15株式市場が暴落する理由
16私を撃ってはいけない、私はピアノだけだ
17失うものは何もない
18他にも選択肢があります
 索引
2ed序文：
Debunking Economics was far from the first book to argue that neoclassical economics was fundamentally unsound. If cogent criticism alone could have brought this pseudo-science down, it would have fallen as long ago as 1898, when Thorstein Veblen penned ‘Why is economics not an evolutionary science?’ (Veblen 1898). Yet in 1999, when I began writing Debunking Economics, neoclassical economics was more dominant than it had ever been.
2001年に初版
第2版は金融危機を予言した12人のリストが引用、紹介されている

NOTES
Chapter 4 
1 In fact, the advanced courses also ignore these more difficult critiques, which means that students who do them, if anything, are even more ignorant than undergraduates.
 2 This last paper –‘Debunking the theory of the firm –a chronology’ –is freely downloadable from www.paecon.net/ PAEReview/ issue53/ KeenStandish53. pdf.
http://www.paecon.net/PAEReview/issue53/KeenStandish53.pdf
^
Milton Friedman (1953). “The Methodology  of Positive  Economics”,  in  Essays in Positive Economics, University  of Chicago Press, Chicago:  3-43. 
Steve Keen (1993a). “The misinterpretation  of Marx's  theory  of value”,  Journal of the  History of Economic Thought, 15 (2), Fall, 282-300. Steve Keen (1993b). “Use-value, exchange-value,  and the  demise of Marx’s  labor theory  of value”,  Journal  of the History of Economic Thought, 15 (1), Spring, 107-121. Steve Keen  (2001).  Debunking Economics, Pluto Press & Zed Books, Sydney & London.
 (2004a). “Why  economics must abandon its theory  of the  firm”, in Salzano, M., & Kirman, A. (eds.),  Economics: Complex Windows, Springer, New  York, pp. 65-88.
 (2004b). “Deregulator: Judgment Day for Microeconomics”,  Utilities Policy, 12:  109 –125.
 (2004c). “Improbable, Incorrect or Impossible: The persuasive but flawed  mathematics of microeconomics”, in Fullbrook,  E. (ed.),  Student's  Guide to  What's  Wrong  with Economics, Routledge, London, pp. 209-222. Steve Keen  and Russell  Standish  (2005). “Irrationality in the neoclassical definition of rationality”,  American  Journal  of Applied Sciences  (Sp.Issue): 61-68. Steve  Keen  and Russell Standish  (2006).  “Profit Maximization, Industry  Structure, and Competition: A  critique  of neoclassical theory”,  Physica A  370: 81-85. 
Piero  Sraffa (1930). “Increasing  Returns  And The  Representative Firm  A Symposium”, Economic Journal 40  pp.79-116. 
George J. Stigler (1957), Perfect competition, historically  contemplated.  Journal of Political Economy  65: 1-17. 

http://www.debtdeflation.com/blogs/debunking-economics/
付録46頁分
http://www.debtdeflation.com/blogs/wp-content/uploads/books/Keen_supplement.pdf

労働者、資本家、銀行家の所得シェア
（大平穏→格差拡大）
















tomomori
ベスト100レビュアー
5つ星のうち5.0「私の目的は新古典派経済学を抹殺することです」
2016年10月29日
形式: ペーパーバックAmazonで購入
2008年の金融危機以降、経済学界は大騒ぎになり、騒ぎの中でオランダの経済学者Dirk Bezemer氏が「アカデミックな手続きでもって金融危機到来を予言した経済学者」を探し求め、12人の経済学者を見つけた。以下、国籍と名前を挙げてみる。Steve Keen（本書の著者、豪州人）、Michael Hudson（米国人）、Dean Baker（米国人）、Wynne Godley（英国人）、Fred Harrison（英国人）、Eric Janszen（米国人）、Jakob Brøchner Madsen（デンマーク人）、Jens Kjaer Sørensen（デンマーク人）、Kurt Richebächer（ドイツ人）、Nouriel Roubini（米国人）、Peter Schiff（米国人）、Robert Shiller（米国人）。
国籍まで挙げてみたのは、「ノーベル経済学賞が米国人学者だけに行くのは何故だ」という疑問に対して、まあ米国人経済学者は確かに優秀だと言えないだろうか、と思い。ただしこの12名の皆さんはノーベル経済学賞を受けてきた学派とは無縁な方々ばかりなんだが。ちなみにロバート・シラー教授は2013年にノーベル経済学賞を受けた。行動経済学で。さて、以上12名の皆さんの分析上の着眼点には共通点があった。以下である。
１、金融資産と実体経済資産の違い。２、両者の資産をファイナンスするクレディットフロー。３、金融資産増加に伴う負債増加。４、金融部門と実体経済部門の会計上の関係性。
中には鬼籍に入った方々もいるが、この12名の皆さんは金融危機後に目出度くスター学者として名を馳せ、著書は売れ、各国の講演会や経済フォーラムで引っ張りだこになった…というのは置いといて、この四点を見て、私も含めて経済学を一度も学んだことのない人々は驚愕する訳である。「え、他の経済学者はこーゆー点を見てなかったってこと？？」と。どうも見てなかったらしい。見ないのが経済学だったらしい。正確には主流派経済学（新古典派）だが。金融危機後、これらの点を無視して「経済分析」をしてきたのが主流派だったのだと一般ピープルにまでバレバレになり、新古典派経済学への批判本が怒涛の如く出版された。しかし本書はそれらの大多数とはちょっと違う。内容がテクニカルでプロ向けなのだ。
で、懺悔すると、私は本書を五年前に買って半分まで呻吟しながら読むも、読了ならずであった。難しいんですもん。キーン教授は元々は物理学者を目指した若者だったが、大学で経済学を専攻した。そして新古典派に出会い、天啓に打たれる。「インチキじゃないか」と。以来、何十年か知らないが、このインチキ学問をテクニカルな領域で破壊してやると燃え続けた。教授の怒りと侮蔑の気焔がなかなかヴィヴィッドでシロートでも味わえる文章部分はかなりある。しかし扱う学問領域があまりに広い。コンピュータ理論なども登場する。教授は全方面から新古典派に攻撃をかけている。同時に、学部学生使用の新古典派系教科書に沿ってテクニカル批判をかけているので、元経済学部学生でもない私にはついていけない。

という訳で、半ばで白旗を上げた読者なんだが、本書は欧米でかなり売れた本らしいし、日本でも誰かがレビューをしてくれるんじゃないかと待っていた。しかし五年経ってもレビュー欄がブランクなもので、挫折組の私がこのようなレビューを上げてみた次第。経済学部の学生さん、読んで下さい。

ーーー
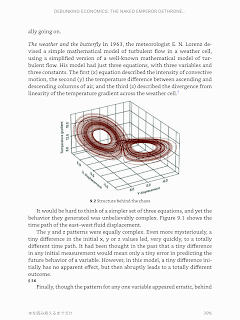
11.2 How speculators actually behave

17.1 A graphical representation of Marx’s dialectics






posted by yoji at 5:35 午前 31 comments

月曜日, 4月 29, 2019

カオス理論

カオス現象の発見とその影響 The Discovery of Chaotic Behavior and its Effects
上田  睆亮（早稲田大・理工  /  理化学研究所）  
https://www.jstage.jst.go.jp/article/japannctam/58/0/58_0_3/_pdf
複雑系
https://nam-students.blogspot.com/2019/05/blog-post_30.html
カオス理論
https://nam-students.blogspot.com/2019/04/blog-post_62.html@ 
ブルックヘブン国立研究所に永久保存されている、
1961年世界初の上田の手によるカオスを示したグラフ
https://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%88%E3%83%A9%E3%82%AF%E3%82%BF%E3%83%BC

アトラクター（英: attractor）は、ある力学系がそこに向かって時間発展をする集合のことである。

その力学系において、アトラクターに十分近い点から運動するとき、そのアトラクターに十分近いままであり続ける。アトラクターの形状は点や曲線、多様体、さらにフラクタル構造を持った複雑な集合であるストレンジアトラクターなどをとりうる。

カオスな力学系に対してアトラクターを描写することは、現在においてもカオス理論における一つの研究課題である。

アトラクターに含まれる軌道は、そのアトラクターの内部にとどまり続けること以外に制限はなく、周期的であったり、カオス的であったりする。☆


参考：
Ananalysis of the Keen model for credit expansion, asset price bubbles and financial fragility M. R. Grasselli · B. Costa Lima 2011
https://ms.mcmaster.ca/~grasselli/GrasselliCostaLima_MAFE_online.pdf
^参照
9. Keen, S.: Finance and economic breakdown: modeling Minsky’s “Financial Instability Hypothesis” . J. Post Keynes. Econ. 17(4), 607–635 (1995)
https://keenomics.s3.amazonaws.com/debtdeflation_media/papers/Keen1995FinanceEconomicBreakdown_JPKE_OCRed.pdf
[^Goodwin, R.M.: A growth cycle. In: Feinstein, C.H. (ed.) Socialism, Capitalism and Economic Growth, pp. 54–58. Cambridge University Press, Cambridge (1967)]
Goodwin関連 http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=S0121-47722010000200001
10. Keen, S.: The nonlinear economics of debt deation. In: Barnett, W.A. (ed.) Commerce, Complexity, and Evolution: Topics in Economics, Finance, Marketing, and Management. Proceedings of the Twelfth International Symposium in Economic Theory and Econometrics, pp. 83–110, Cambridge University Press, New York (2000)
11. Keen, S.: Household debt: the nal stage in an articially extended Ponzi bubble. Aust. Econ. Rev. 42(3), 347–357 (2009)
http://www.rogerfarmer.com/rogerfarmerblog/2016/10/4/nho932exasra0c2a2amkvdmovcy9rz
https://translate.google.com/translate?sl=auto&tl=ja&u=http%3A%2F%2Fwww.rogerfarmer.com%2Frogerfarmerblog%2F2016%2F10%
2F4%2Fnho932exasra0c2a2amkvdmovcy9rz

スティーヴ・キーン『次なる金融危機』
https://nam-students.blogspot.com/2019/04/can-we-avoid-another-financial-crisis.html
経済入門書は多く出版されているが本書は別格である。
塩沢由典
https://nam-students.blogspot.com/2019/04/blog-post_20.html
進化経済学（Evolutionary economics）
https://nam-students.blogspot.com/2019/05/evolutionary-economics.html
リカード『経済学および課税の原理』(On the Principles of Political Economy, and Taxation)
http://nam-students.blogspot.jp/2015/04/on-principles-of-political-economy-and_25.html
マルクス・インデックス
　http://nam-students.blogspot.com/2013/04/blog-post_0.html
NAMs出版プロジェクト: 価値形態論（逃走論 1984,1986）　

藤本隆宏 現場指向企業と製品・工程イノベーション : PXNWモデルによる予備的分析
https://nam-students.blogspot.com/2019/02/the-fractal-keynesian-stimulus-by-csr.html
カオス理論
https://nam-students.blogspot.com/2019/04/blog-post_62.html@

https://compenn.exblog.jp/438844/

がんばれ！日本人研究者（2）；上田睆亮（よしすけ）

a0010614_154121.jpg
　　上田氏（京都大学電気工学科教授）はすでに世界のウエダ先生ですから、私のようなものががんばれ！などとエールを送るような立場ではないのですが、日本人の偉大な研究者ということで紹介させていただきます。それでこれもすでに一度書きましたが、世界で一番最初にカオス現象を発見したのが上田氏です。一般的には気象学者のローレンツが有名になっていますが、上田氏が1961年、ローレンツが1963年に発表しています。
　　上田氏はすでに博士課程の1年のときにカオス現象に着目し、平日には他の研究を進めながら、アフターファイブや土日を使ってコンピュータでのシュミレーション実験を行っていました。日本では海外での研究結果に基づいてそれを発展させる形での研究を行うスタイルが多い中で、上田氏はまったく独自の観点で独創的な研究を押し進め、そのためなかなか周囲から理解されずに大変苦労されたようです。そしてその研究はむしろ海外の研究者によって注目されました。例えば最初に「カオス」という言葉を使ってカオスブームに火を付けた李天岩（リ・ティェンイェン）やジェームズ・ヨークも上田氏に早くから注目しました。
　　上田氏の若い研究者への言葉；「若い人に私が言いたいのは、あまり他人の言うことを気にしては駄目だよ！自分の好きなことを一生懸命やりなさい！」「とにかく自分で汗を流しなさい。研究は頭だけでは出来ないのです。」
（図はニューヨークのブルックヘブン国立研究所に永久保存されている上田氏のカオスのオリジナルデータ。1961年11月27日の日付になっている。）

参考書；『複雑系を越えて』 




カオス性を持つローレンツ方程式の解軌道
カオス理論（カオスりろん、英: chaos theory、独: Chaosforschung、仏: Théorie du chaos）は、力学系の一部に見られる、数的誤差により予測できないとされている複雑な様子を示す現象を扱う理論である。カオス力学ともいう[1][2]。
ここで言う予測できないとは、決してランダムということではない。その振る舞いは決定論的法則に従うものの、積分法による解が得られないため、その未来（および過去）の振る舞いを知るには数値解析を用いざるを得ない。しかし、初期値鋭敏性ゆえに、ある時点における無限の精度の情報が必要であるうえ、（コンピューターでは無限桁を扱えないため必然的に発生する）数値解析の過程での誤差によっても、得られる値と真の値とのずれが増幅される。そのため予測が事実上不可能という意味である。

目次

カオスの定義と特性編集

ある初期状態が与えられればその後の全ての状態量の変化が決定される系を力学系と呼ぶ[3]。特に、決定論に従う力学系を扱うことを強調して決定論的力学系とも呼ばれる[4]。カオス理論において研究されるカオスと呼ばれる複雑で確率的なランダムにも見える振る舞いは、この決定論的力学系に従って生み出されるものである[5]。この点を強調するためカオス理論が取り扱うカオスを決定論的カオス(deterministic chaos)とも呼ぶ[3]。複雑で高次元の系ではなくとも、1次元離散方程式や3次元連続方程式のような非常に簡単な低次元の系からでも、確率的ランダムに相当する振る舞いが生起される点が決定論的カオスの特徴といえる[6][7]。この用語は、カオス理論以前から存在するボルツマンにより導入された分子カオスと呼び分ける意味合いもある[8]。ボルツマンによるカオスは確率論的乱雑さを表しており、カオス理論におけるカオスとは概念が異なる。
カオス理論におけるカオスの厳密な定義は研究者ごとに違い、まだ統一的な定義は得られていない[9][10]。できるだけ簡単な表現でまとめると、カオスの定義あるいはカオスと呼ばれるものの特性とは、「非線形な決定論的力学系から発生する、初期値鋭敏性を持つ、有界な非周期軌道」といえる[11][12][13][14]。また、このような軌道を含む力学系の性質を指してカオスとも呼ぶ[5][15][16]。軌道を指していることを明らかにする場合はカオス軌道(chaotic orbit)と呼ぶ場合もある[13][16]。以下に、もう少し詳細に説明する。

非線形性編集

力学系には大きく分けて線形力学系と非線形力学系が存在するが、線形力学系ではカオスは発生しない[17]。その系からカオスが生起されるためには、系が何らかの非線形性(nonlinearity)を持つ必要がある[18][14]。言い換えると、軌道を生成する系が非線形力学系であることは、その系からカオスが生起されるための必要条件である。これの十分条件は満たされず、すなわち、非線形力学系であれば必ずカオスが生起するわけではない。以下に述べる特性と違い、非線形性はカオス軌道自体の特性というよりは、カオスを生起する系の特性である。

初期値鋭敏性編集

カオスの定義あるいは特性として第一に挙げられるのが初期値鋭敏性(sensitivity to initial conditions)である[19][20][注釈 1]。これは、同じ系であっても初期状態に極僅かな差があれば、時間発展と共に指数関数的にその差が大きくなる性質である[5]。この性質は軌道不安定性(orbital instability)と言い換えられることもある[24][25][26]。定量的には、この初期値鋭敏性は、リアプノフ指数、コルモゴロフ-シナイエントロピーなどで評価される[25][27]。
初期値鋭敏性により極めて小さな差も指数関数的に増大していくので、初期値鋭敏性を有する実在の系の将来を数値実験で予測しようとしても、初期状態（入力値）の測定誤差を無くすことはできないので、長時間後の状態の予測は近似的にも不可能となる[28][25][26]。このような性質は長期予測不能性(long-term unpredictability)[25]や予測不可能性(unpredictablity)[28]などとも呼ばれる。一方で、例えカオスであっても決定論的法則から発生されるものであるため、短時間内であれば有用な予測は可能といえる[29][14]。以上のような性質は、標語的にバタフライ効果(butterfly effect)と呼ばれる。

有界性編集

初期値鋭敏性、すなわち指数関数的に初期状態の差が広がる軌道を有する系というだけでは、カオスには該当しない[14][30]。カオス軌道であるためには軌道がある有界な範囲に収まる必要がある[14][12][13]。このようなカオスの特性は有界性(boundedness)とも呼ばれる[25]。
初期値鋭敏性のみではカオスとならない例として、x_{{n+1}}=ax_{n}という単純な等比数列形式の離散力学系の写像が考えられる[30]。これに対して初期値が異なる2つの軌道を考えると、初期値の差をδとすれば、その差はa^{{n}}\delta で表せる。よって、これら2つの軌道は離散時間nが増加すれば指数関数的に差が開いていくので、系は初期値鋭敏性を有するといえる。しかし、これらの軌道はx_{n}=x_{0}\ a^{{n}}で示される単純な指数関数曲線であり、有界な領域に収まらず発散してしまい、非周期的な軌道も存在しない。

非周期性編集

カオスの特徴は、平衡点に収束するわけでもなく、周期的軌道に漸近するわけでもなく、非周期的な軌道を取る点である[16][6][13]。カオスが認識されるようになる以前は、非周期的な運動が発生するには、発生させる系自体も複雑なものだろうと考えられていたが、非常に簡単な決定論的な法則（力学系）からでも非周期運動が発生する点がカオスの特徴である[31]。平衡点収束と周期的軌道以外にも力学系では準周期的軌道と呼ばれる軌道も存在し、非常に複雑で不規則的な軌道を取るが、初期値鋭敏性を持たないことからカオスには分類されない[5]。カオスが非周期軌道を取ることの特性は非周期性(nonperiodicity)などと呼ばれる[25]。非周期的であるかどうかは、パワースペクトルが幅のある連続的スペクトルを示すかどうかなどで評価される[25][32]。

数学的定義の例編集

カオスの数学的定義として、しばしば引用される、位相的方法による標準的な定義であるロバート・デバニー(Robert L.Devaney)の定義がある[33][9][34]。これを例として以下に示す。
次の3つの条件を満たす写像f: V → Vは、Vの上でカオス的であるといえる[35]。
  1. 初期条件に鋭敏に依存する。
  2. 位相的に推移的である。
  3. 周期点はVにおいて稠密である。
ここで、条件1は次の条件を満たすことである[36]。
fの反復合成写像をfnとしたとき、任意のx ∈ Vと、xの任意の近傍Nに対して、\left|f^{n}(x)-f^{n}(y)\right\vert >\delta を満たすような、y ∈ N、n > 0、δ > 0が存在する。
条件2は次の条件を満たすことである[36]。
任意の開集合の対U, J ⊂ Vに対して、fk(U) ∩ J ≠ ∅を満たすような、k > 0が存在する。
条件3は次の条件を満たすことである[37]。
周期点の集合Yの閉包cl(Y)が、cl(Y) = Vである。

研究史編集

カオス命名以前編集

カオス理論誕生以前にも、カオスの性質の1つである初期値鋭敏性の存在について既に指摘されていた[20]。ジェームズ・クラーク・マクスウェルが、1877年の著書「物質と運動」の冒頭中で、『「同じ原因は常に同じ結果を生み出す」という、よく引用される原則がある。もう一つの原則として、「似た原因は似た結果を生む」というものがある。多くの物理現象はこれを満たすような状態にあるが、小さな初期状態の違いがシステムの最終状態に非常に大きな変化をもたらす場合もある』と述べている[38][39]。さらにマクスウェルは、続く注記の中で『気象現象は局所的な不安定性の限りない集まりに起因するような現象かもしれず、1つの有限な法則体系に全く従わないような現象かもしれない』と述べており[39]、後にローレンツが指摘するような気象現象の不安定性を指摘している[38]。
19世紀における一般的な非線形微分方程式の解法手法は、ウィリアム・ローワン・ハミルトン等の成果に代表される積分法（積分、代数変換の有限回の組み合わせ）による求解と、微小なずれを補正する摂動法である。この積分法による解が得られる系を、ジョゼフ・リウヴィルは可積分系と呼んだ。その条件は、保存量の数が方程式の数（自由度）と一致することであった。
カオス理論の始まりともされる系統的研究の最初のものとしては、アンリ・ポアンカレによる仕事が挙げられる[40]。1880年代、ポアンカレは、三体問題の研究において、非周期的で、増加し続けないまたは固定点へ到達しない軌道があり得ることを発見した[41][42]。1892年から1899年、ポアンカレは、三体問題では保存量が不足し積分法による解析解が得られないことを証明した（このような系を非可積分系と呼ぶ）。彼は、この場合に軌道が複雑となることを示唆している。ただし、この時点では、その実態は認識されていなかった。
実在の系でカオス運動を観察したと考えられる例としては、1927年のファン・デル・ポール(en:Balthasar van der Pol)とファン・デル・マークによる実験報告が挙げられる。彼らは1927年の論文において非線形電気回路の実験における周波数非増加(Frequency demultiplication)と呼ぶ現象を報告した[43]。これは彼らが構成した非線形な電気回路において、コンデンサの容量Cをパラメータ的に増加させていくと、回路の発振周波数ωがω/2, ω/3, ω/4,...という風に非連続的に移り変わっていく現象である[44]。特に、ファン・デル・ポールらは、このような発振周波数の非連続的な遷移の前に不規則な雑音(irregular noise)が発生することを報告している[44]。小室元政らは、実在の系によるカオス現象の報告はこの実験が最初だろうと推測している[45]。しかし、ファン・デル・ポールらは、この現象を副次的な現象(subsidiary phenomenon)と見なして、それ以上の研究は続けなかった[46]。
1940年代、アンドレイ・コルモゴロフ、V.B.チリコフ等により、このハミルトン力学系（例えば、多体問題といった散逸項の無いエネルギーが保存される系）のカオス研究が進められた。大自由度ハミルトニアン系カオスは、統計力学の根源に結びつくものでもあるが、その定義すら困難であり今後の研究が期待される。

カオス命名と研究の隆盛編集

1961年、エドワード・ローレンツにより、簡単な微分方程式から作られる天気予報の気象モデルの数値計算結果がカオス的な振る舞いをすることが発見された。1963年、この結果はテント写像により引き起こされるカオスとして発表された[47]。このタイプのカオスは、ローレンツカオス（後述するカオスの例）と呼ばれ、ローレンツ・アトラクタを持つことでも有名である。しかし、このローレンツの論文は当時はほとんど注目を集めることなく埋もれてしまった[48]。
また京都大学工学部の上田睆亮は、1961年に既に、非線形常微分方程式を解析する電気回路で発生したカオスを物理現象として観測し、不規則遷移現象と称してカオスの基本的性質を明らかにしていた。しかし、日本の学会ではその重要性が認識されず長い間日の目を見なかった。この上田が発見したストレンジ・アトラクタは、後の1980年にフランスの数学者ダビッド・リュエルによりジャパニーズ・アトラクタと命名され、日本海外でも知られるようになった[49]。
これらの複雑な軌道の概念は1975年、ジェイムズ・A・ヨークとリー・ティエンイエンによりカオスと呼ばれるようになった。また、マンデルブロ集合で有名なブノワ・マンデルブロなどにより研究が進んだ。
一方では、非線形方程式の中にはソリトン（浅水波のモデル）のように無限の保存量を持ち、安定した波形を保ち将来予測の可能な、解析的な振る舞いが明らかになっているものもあり、カオスとは対極にある存在である。しかし、ソリトンと言えども、連続無限自由度を扱うような特殊な場合で可積分系が破れることがあり、その場合カオスになることが指摘された。

カオスの一例編集

ロジスティック写像編集

詳細は「ロジスティック写像」を参照
二次方程式を用いた写像
X_{n+1}=aX_n(1-X_n) : 0 \le a \le 4,\ 0 \le X_0 \le 1
をロジスティック写像と呼ぶ。もともとロジスティック方程式という連続時間の微分方程式として、19世紀から知られていたが、写像として時間を離散的にすることで、極めて複雑な振舞いをすることが1976年、ロバート・メイによって明らかにされた。
ロジスティック写像は生物の個体数が世代を重ねることでどのように変動していくのかのモデルとして説明される。ここで a（下図の横軸）が繁殖率、X_{n}（下図の縦軸）がn世代目の個体数を表している。
  • a\le3 のとき、個体数X_{n}はある一定の値に収束する。
  • 3<a\le3.56995 のときについては、まずaが3を超えたところでX_{n}が2つの値を繰り返す様になる。さらにaが1+\sqrt{6}より大きくなるとX_{n}のとる値が4つ、8つと増加していく。この周期逓倍点の間隔は一定の比率ファイゲンバウム定数で縮まる。
  • 3.56995<a のとき、X_{n}のとる値に規則性が見られなくなる。この境界値3.56995をファイゲンバウム点と呼ぶ。周期逓倍点の間隔が0に収束し、周期が無限大に発散したのであるが、場所によっては3と7の周期性が戻る。この部分は"窓"と呼ばれる。
この様に単純な二次方程式から複雑な振る舞いが発生し、また a=4 付近では初期値X_{0}のわずかな違い（例えば0.1と0.1000001）が将来の値X_{n}に決定的な違いをもたらしている。

ロジステック写像 x → r x (1 ? x )
横軸はaを、縦軸はX_{n}の収束する値を表している。a=3 で2値の振動へと分岐し、更に分岐を繰り返していくことが分かる。

実際の個体数の変動編集

a=3 の場合。2/3に収束するが、非常に収束が遅い。
Chaos(a3).png
a=3.9 の場合。規則性のない変動となる。
Chaos(a３．９).png

カオスの判定編集

カオスにはその必要十分条件が与えられていないことから、カオスの判定は複数の定義の共通を持って、カオス性があるという判定以外に方法が無い。このため、カオスの判定とは必要条件という性質を持つ。多くは、スペクトルの連続性、ストレンジアトラクタ、リアプノフ指数、分岐などを以ってカオスと判定している。
しかしながら、ただのランダムノイズであっても、リアプノフ指数が正になるといった事例が指摘され、こういった面よりノイズとカオスは区別はつかない。そのため、例えばリアプノフ指数や、何をもってストレンジアトラクタと見なすかの指標をそのまま信用してカオスと判定して良いかという問題が起きる。
1992年に、ノイズか決定論的システムから作成されたデータかどうかを検定する「サロゲート法」が提案された。サロゲート法は基本的には統計学における仮説検定にもとづく手法であるため、与えられたデータが検定にパスした場合でも、そのデータについて「仮定したノイズであるとは言いがたい」という主張はできるが、「カオスである」という断定をすることはできず、その意味で決定的な検定方法ではない。以下サロゲート法の概要について説明する。

サロゲート法編集

サロゲート法には様々な方法がある。代表的な「フーリエ変換型サロゲート法」について述べる。
帰無仮説: 元時系列は、（予め仮定する）ノイズである
有意水準をαとする
  1. 元時系列のパワースペクトルを計算
  2. パワースペクトルを元時系列とし、位相をランダムに設定した新スペクトルをN個作成
  3. 新スペクトルをフーリエ逆変換して、新時系列をN個作成（これらをサロゲートデータと呼ぶ）
  4. 元の時系列の統計値<N個の新時系列の統計値の下α/2を与える値 または N個の新時系列の統計値の上α/2を与える値<元の時系列の統計値 → 帰無仮説棄却（ノイズとは言えない）

脚注編集

注釈編集

  1. ^ 「初期値に対する鋭敏な依存性」[21]、「鋭敏な初期値依存性」[22]、「初期値鋭敏依存性」[23]、など表記にばらつきはある。

出典編集

  1. ^ 下條 1992.
  2. ^ 早間 2002.
  3. ^ a b 合原・黒崎・高橋 1999, p. 228.
  4. ^ 井上 1997, p. 51.
  5. ^ a b c d 下條 1992, p. 2.
  6. ^ a b 井上 1997, p. 81.
  7. ^ 合原 2011, p. 7.
  8. ^ Devaney 1990, p. 267.
  9. ^ a b 合原 1990, pp. 14-16.
  10. ^ 合原・黒崎・高橋 1999, p. 44.
  11. ^ 合原 1990, p. 1.
  12. ^ a b 船越 2008, p. 14.
  13. ^ a b c d アリグッド・サウアー・ヨーク 2012, p. 120.
  14. ^ a b c d e 井上 1997, p. 56.
  15. ^ Lorenz 1997, p. 19.
  16. ^ a b c 森・蔵本 1994, p. 135.
  17. ^ 井上 1997, p. 54.
  18. ^ 合原・黒崎・高橋 1999, p. 14.
  19. ^ アリグッド・サウアー・ヨーク 2012.
  20. ^ a b エイブラハム・ウエダ 2002, p. 165.
  21. ^ 合原・黒崎・高橋 1999, p. 230.
  22. ^ 下條 1992, p. 261.
  23. ^ エイブラハム・ウエダ 2002, p. 192.
  24. ^ 船越 2008, p. 170.
  25. ^ a b c d e f g 合原 2011, p. 9.
  26. ^ a b 森・蔵本 1994, p. 151.
  27. ^ 下條 1992, p. 109.
  28. ^ a b 船越 2008, p. 11.
  29. ^ Grebogi/Yorke 1999, p. 2.
  30. ^ a b 船越 2008, p. 12.
  31. ^ 井上 1997, p. 26.
  32. ^ 下條 1992, p. 64.
  33. ^ Weisstein, Eric W. “Chaos”. MathWorld. Wolfram Research. 2014年12月11日閲覧。
  34. ^ 早間 2002, p. 57.
  35. ^ Devaney 1990, p. 40.
  36. ^ a b Devaney 1990, p. 39.
  37. ^ Devaney 1990, p. 13.
  38. ^ a b 山口昌哉・蔵本由紀. “複雑な現象に立ち向かう現代物理学 多様性に潜む「コト」の不変性　Chap.2”. Science Talk. 東芝. 2014年12月10日閲覧。
  39. ^ a b Maxwell, James Clerk, Larmor, Joseph, Sir. “Matter and motion pp.13-14”. California Digital Library. University of California Libraries. 2014年12月10日閲覧。
  40. ^ Grebogi/Yorke 1999, p. 29.
  41. ^ Jules Henri Poincare (1890) "Sur le probleme des trois corps et les equations de la dynamique. Divergence des series de M. Lindstedt," Acta Mathematica, vol. 13, pages 1?270.
  42. ^ Florin Diacu and Philip Holmes (1996) Celestial Encounters: The Origins of Chaos and Stability, Princeton University Press.
  43. ^ B. van der Pol and J. van der Mark (1927) "Frequency demultiplication," Nature, vol. 120, pages 363?364. See also: Van der Pol oscillator
  44. ^ a b 合原 1990, p. 21.
  45. ^ 合原 1990, p. 20.
  46. ^ エイブラハム・ウエダ 2002, p. 158.
  47. ^ Edward N. Lorenz, "Deterministic non-periodic flow," Journal of the Atmospheric Sciences, vol. 20, pages 130?141 (1963).
  48. ^ 合原・黒崎・高橋 1999, p. 43.
  49. ^ エイブラハム・ウエダ 2002, p. 53.

参考文献編集

  • 下條隆嗣、1992、『カオス力学入門　―古典力学からカオス力学へ』初版、 近代科学社〈シミュレーション物理学6〉 ISBN 4-7649-2005-0
  • Robert L. Devaney、後藤憲一（訳）、1990、『カオス力学系入門　第2版』初版、 共立出版 ISBN 4-320-03280-2
  • 合原一幸・黒崎政男・高橋純、遠藤諭（編）、1999、『哲学者クロサキと工学者アイハラの神はカオスに宿りたもう』初版、 アスキー ISBN 4-7561-3133-6
  • 井上政義、1997、『やさしくわかるカオスと複雑系の科学』初版、 日本実業出版社 ISBN 4-53402492-4
  • ラルフ・エイブラハムほか、ラルフ・エイブラハム、ヨシスケ・ウエダ（編）、稲垣耕作・赤松則男（訳）、2002、『カオスはこうして発見された』初版、 共立出版 ISBN 4-320-03418-X
  • Celso Grebogi, James A. Yorke（編）、香田徹ほか（訳）、1999、『カオス・インパクト　―カオスは自然科学と社会科学に何をもたらしたか』第1版、 森北出版 ISBN 4-627-21321-2
  • 合原一幸ほか、合原一幸（編）、1990、『カオス　―カオス理論の基礎と応用』初版、 サイエンス社 ISBN 4-7819-0592-7
  • 池口徹・山田泰司・小室元政、合原一幸（編）、2011、『カオス時系列解析の基礎と応用』第4刷、 産業図書 ISBN 978-4-7828-1010-1
  • 船越満明、2008、『カオス』初版、 朝倉書店〈シリーズ 非線形科学入門3〉 ISBN 978-4-254-11613-7
  • K.T.アリグッド・T.D.サウアー・J.A.ヨーク、シュプリンガー・ジャパン（編）、津田一郎（監訳）、星野高志・阿部巨仁・黒田拓・松本和宏（訳）、2012、『カオス　第1巻　力学系入門』、丸善出版 ISBN 978-4-621-06223-4
  • E. N Lorenz、杉山勝・杉山智子（訳）、1997、『ローレンツ　カオスのエッセンス』初版、 共立出版 ISBN 4-320-00895-2
  • 森肇・蔵本由紀、1994、『散逸構造とカオス』、岩波書店 ISBN 4-00-010445-4
  • 早間慧、2002、『カオス力学の基礎』改訂2版、 現代数学社 ISBN 4-7687-0282-1

関連項目編集



☆

力学系は一般的にひとつあるいは複数の微分方程式あるいは差分方程式により表される。これらの方程式は短い時間区間における力学系の挙動を記述するので、より長い時間区間における力学系の挙動を決定するためには、その方程式を積分する必要がある。このためにしばしばコンピュータが効果的に用いられる。

実世界における力学系は散逸的であることが多いとされる。すなわち、もし力学系に運動の駆動力が無ければ、運動は停止するものと考えられている（そのような散逸は、様々な原因による内部摩擦や熱力学的損失、物質の損失などにより生じうる）。散逸と駆動力が組み合わさることにより、初期の摂動を鎮め、その力学系の振る舞いを典型的なものへと落ち着かせる傾向にある。そのような典型的な振る舞いに対応している力学系からなる位相空間の一部分はattracting section または attractee と呼ばれる。

アトラクターに似たような概念として、不変集合や極限集合が挙げられる。不変集合とは、ある力学系に対して、その集合自身に時間発展するような集合のことである。アトラクターは不変集合を含むことがある。極限集合とは、力学系の軌道の各点から、時間が無限大に向かうときに近づく点の集合である。アトラクターは極限集合であるが、アトラクターではない極限集合も存在する。ある種の力学系において、いくつかの点においては極限集合から外れる摂動を与えられた時にも収束するが、他のいくつかの点では「はねとばされて」二度とその極限集合の近くに戻らないことがあり得る。

減衰振子を例に考える。減衰振子は2つの不変集合（不動点）を持つ。最も低い位置にある x_{0} と最も高い位置にある x_1 である。

軌道はx_{0}に収束するので、x_{0}は極限集合であるが、x_1 は極限集合ではない。エネルギー散逸があるため、x_{0} はアトラクターでもある。振り子の振動が減衰せず、エネルギーの散逸がなければ、x_{0} はアトラクターにはならない。

数学的定義編集

f(t, •) を、力学系の運動状態を決定づける関数として、以下のように定義する。ある時間 t = 0 における系の状態を表す位相空間上の点を a とすると、f(0, a) = a である。また、正の値 t > 0 に対しては、f(t, a) はその状態 a が時間 t だけ経過して発展した状態を与える。例えば、一次元空間上で座標 x から速度 v で等速直線運動する粒子（t = 0 での位相空間上での座標が (x, v) ）の力学系の f は

f(t, (x, v)) = (x + tv, v),\

と表せる。

アトラクターは、位相空間の部分集合 A で以下の三つの条件を満たすようなものである。

  • 集合 A は関数 f に対し前方不変である。すなわち、a ∈ A ならば、任意の t > 0 に対して f(t, a) ∈ A である。
  • Aのある近傍で吸引流域 (basin of attraction) B(A) が存在する。B(A) は極限 t → ∞ において集合 A に含まれるすべての点 b からなる集合である。より厳密に言えば、B(A) は以下の性質を満たすようなすべての点 b からなる集合である。
    集合 A の任意の開近傍 N に対し、ある正の定数 T > 0 が存在し、f(t, b) ∈ N が任意の実数 t > T に対して成立する。
  • 集合Aの真部分集合で上の二つの性質をみたすようなものは存在しない。

吸引流域は集合 A を含むようなある開集合を含むため、A に十分近いすべての点は A に吸引されることとなる。アトラクターの定義では、考えられている位相空間上の距離を用いたが、基本的には定義の指す内容は距離関数のとり方によらず位相空間のトポロジーにのみ依存する。Rn の場合では、一般的にユークリッドノルムが用いられる。

アトラクターの定義に関しては、文献により多くの異なる定義がなされることがある。 例えば、点がアトラクターとなることを避けるためにアトラクターは正の測度を持つべきであると制限をかけたり、B(A)が近傍でなくてはならないという条件を緩めたりしている。

アトラクターの形状の種類編集

アトラクターは力学系の位相空間の部分集合である。1960年代頃の教科書によると、それまではアトラクターは位相空間の「幾何学的な」部分集合（点、直線、曲面、体積領域）であると考えられていた。観測されていた（位相幾何学的に）「悪い」集合（wild sets）は、取るに足らない例外であると考えられていた。スティーヴン・スメイルは彼の考案した蹄鉄型写像が構造安定であること、およびそのアトラクターがカントール集合の構造を持つことを示すことに成功した。

二つの簡単なアトラクターとしては、不動点とリミットサイクルが挙げられる。その他にも多くの幾何学的な集合がアトラクターであり得る。それらの集合（あるいは集合上での動き）を図示することが困難である場合、そのアトラクターはストレンジアトラクターと呼ばれる（後述）。

不動点編集

複素二次多項式に対する弱い意味で吸引的な不動点

一般的に、不動点とは関数の点で変換に対して変化しないものである。

力学系の発展を一連の座標変換の過程の連続であると見做した時、その全ての過程の下で不動のものとして固定し続ける点が存在する可能性がある。一般的にはそのような点は存在しない場合が多いが、存在する場合もあり得る。

落下する小石や、減衰振子や、グラスの中の水などが最終的に落ち着くような状態である最終状態で、ある力学系がそこに向かうようなものは、その発展関数の不動点に対応し、そのような最終状態はアトラクターにおいても起こるであろうが、その二つの概念は同値であるとはいえない。あるボウルの周囲を回るビー玉は、たとえ物理学的な空間においては不動点を持たなくても、位相空間においては持つ可能性がある。そのビー玉が運動量を失い、そのボウルの底に落ち着いたなら、そのビー玉は物理空間および位相空間において一つの不動点を持ち、その力学系のアトラクターに位置することになる。

リミットサイクル編集

詳細は「リミットサイクル」を参照

リミットサイクルは系の周期的軌道であり、孤立している。例えば振り子時計の振り子、ラジオのチューニング回路、安静時の心拍などがそれに当たる。理想的な振り子は軌道が孤立していないのでリミットサイクルではない。理想的な振り子の位相空間では、周期軌道の任意の点に対して別の周期軌道に属する点が存在する。

リミットトーラス編集

リミットサイクルの状態を通しての系の周期的軌道には複数の周期が存在する場合もある。それら周期のうち2つが無理数を形成するとき、その軌道はもはや閉じておらず、リミットサイクルはリミットトーラスとなる。N_t 個の不整合周期があるとき、このようなアトラクターを N_t-トーラスと呼ぶ。下図は2-トーラスの例である。 Torus.png このアトラクターに対応する時系列（不整合周期を持つN_t周期関数の総和を離散標本化したもの。正弦波である必要はない）は「準周期的 (quasiperiodic)」である。そのような時系列は厳密には周期的ではないが、そのパワースペクトルは鋭い線からのみ成る。

ストレンジアトラクター編集

ローレンツのストレンジアトラクターの図（ρ=28, σ = 10, β = 8/3）

非整数次元のアトラクターやカオス理論でしか振る舞いを説明できない力学系のアトラクターをストレンジであると（非形式的に）いう。元はカオスアトラクターと呼ばれていたが、ダヴィッド・ルエールと Floris Takens が流体の力学系における一連の分岐の結果として生じるアトラクターを指してストレンジアトラクターという造語を使用した。ストレンジアトラクターという場合、カントール集合と非可算無限集合の直積構造を持つことが多い。

ストレンジアトラクターの例として、エノンアトラクター、レスラーアトラクター、ローレンツアトラクター、Tamariアトラクターなどがある。

参考文献編集

ウィキメディア・コモンズには、アトラクターに関連するメディアがあります。

関連項目編集

外部リンク編集

posted by yoji at 1:54 午後 2 comments